Дискретная математика в программировании. Часть VII

1.

Дискретная математика
в программировании
Часть VII
Костюк Ю.Л.
доктор технических наук, профессор

2.

Задача раскраски графа
На географических картах соседние страны должны
раскрашиваться в разные цвета.
Если каждая страна – вершина графа, общая граница соседних стран – ребро, то для
каждой вершины графа нужно задать «цвет» по таким правилам:
1
2
смежные вершины должны быть окрашены в различные цвета, если это условие
выполнено, то раскраска считается правильной;
общее количество различных цветов должно быть минимальным, если это условие
выполнено, то раскраска считается оптимальной.
Граф из n вершин можно просто раскрасить в n цветов, раскраска будет правильной,
но не оптимальной,
Количество вариантов этой раскраски равно количеству перестановок для n чисел:
1∙2∙ . . . ∙ n = n!

3.

Задача раскраски графа
На практике обычно требуется вычислить любую из правильных оптимальных
раскрасок.
Полный граф из n вершин раскрашивается в n цветов.
Дерево легко красится в 2 цвета.
Однако в общем случае для произвольных графов эта задача очень трудная. Даже
для графа с n = 100 вершинами для её решения может потребоваться работа
суперкомпьютера в течение миллионов лет.
На практике раскраски для больших графов вычисляют приближёнными
алгоритмами. Многие такие алгоритмы называют жадными, потому что
в них однажды присвоенный вершине цвет в последующем не изменяется.

4.

Алгоритм 5.
Жадная раскраска графа
Входные данные: граф
1
2
3
Для каждой вершины графа вычисляется её степень
Вершины упорядочиваются по убыванию степеней
Вершины просматриваются по порядку, как они отсортированы
Для очередной вершины проверяется цвет смежных с ней вершин: еще не окрашенные
вершины пропускаются, для окрашенных отмечаются занятые цвета, начиная от 1.
Очередная вершина окрашивается в цвет с минимальным не занятым номером

5.

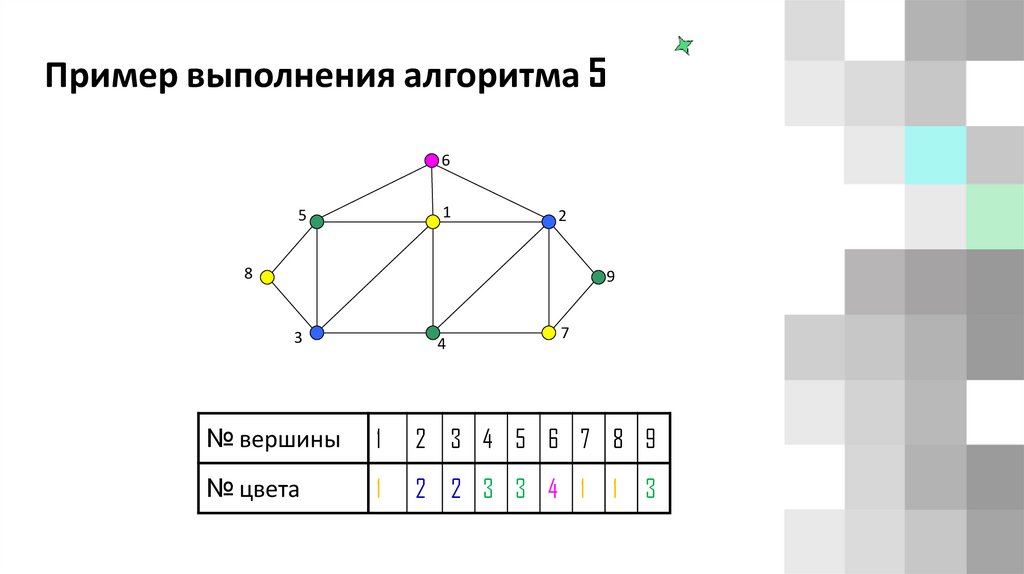
Пример выполнения алгоритма 5
6
1
5
2
8
9
3
4
7
№ вершины
1
2 3 4 5 6 7 8 9
№ цвета
1
2 2 3 3 4 1
1
3

6.

Задача раскраски графа
В задаче раскраски карт граф получается планарным, т.е. таким, что его можно
изобразить на плоскости без пересечения рёбер.
Ещё в XIX веке была выдвинута гипотеза, что планарные графы можно раскрашивать
четырьмя красками.
Только через 100 лет гипотеза стала теоремой, причём из-за большой сложности
доказательство было выполнено с применением компьютера.

7.

Задания для самостоятельной работы
1
2
Задан граф с 8 вершинами и рёбрами: (1,2), (1,3), (1,4), (1,6), (2,7),
(2,8), (4,5). Алгоритмом 5 вычислить раскраску графа и
записать цвета вершин: 1, 2, …, 8 через 1 пробел.
Задан граф с 6 вершинами и рёбрами: (1,2), (1,3), (1,4),
(1,5), (1,6), (2,3), (2,4), (3,5), (5,6). Номера вершин уже
упорядочены по убыванию их степени. Алгоритмом 5
вычислить раскраску графа и записать цвета вершин:
1, 2, …, 6 через 1 пробел.

8.

Спасибо за внимание