Элементы теории множеств

1.

2.

1. Понятия множества.
1)
2)
3)
Что такое множество;
Виды множеств;
Способы задания множества.
2. Подмножество
1)
2)
3)
4)
Понятие подмножества;
Число подмножеств данного множества;
Понятие универсального множества;
Равные множества.
3. Действия над множествами.
1)
2)
3)
4)
Пересечение;
Объединение;
Разность;
Дополнение.
4. Решение задач с использованием кругов Эйлера.

3.

Понятие множества является одним из основных
понятий математики и поэтому не определяется через
другие. Наука о множестве возникла с давних времен.
В IXX веке Георг Кантор ( немецкий математик )
обосновал множество, как «совокупность»,
«собрание», «набор», «ансамбль» и так далее. Многие
математики выдвигали понятие и определения. Один
французский математик дал дословное определение
множеству: «Множество – невообразимое больше чем
ничего, но меньше этого большего на множество». В
наши времена множества используют как понятие
единого целого, составленного из мелких частей –
элементов.

4.

ОПР. 1: Объекты, из которых образовано множество, называют
его элементами.
Обозначение: a, b, c,…, z. Множества обозначают буквами
латинского алфавита: А, В, С,…, Z.
Запись: а А означает, что а – элемент множества А.
ОПР. 2 : Множество, не содержащее ни одного объекта,
называют пустым.
Обозначение:
ОПР. 3: Множество, которое состоит из одного элемента –
называется единичным. Множества бывают конечные и
бесконечные.
ОПР. 4: Множество, которое имеет определенное количество
элементов, называется конечным.
ОПР. 5: Множество, которое имеет бесконечно много элементов,
называется бесконечным.

5.

Предложение вида «Объект а
принадлежит множеству А»
можно записать, используя
символы: а А.
Например,
Окружность М
В М,
О М,
А М,
С М.

6.

1) Бесконечные непериодические дроби:
А = {5,325728…; 6,2853257…;π}
2) Числа, дающие при делении на 6 остаток 5:
В = { 17, 23, 29…} В = { 6к + 5, к Z }
Так, множество дней недели конечно, а
множество точек на прямой бесконечно.
Бесконечными являются и такие множества, как
множество натуральных чисел – N, множество
целых чисел – Z, множество рациональных
чисел – Q, множество действительных чисел –
R.

7.

Характеристическое свойство – это такое
свойство, которым обладает каждый
элемент, принадлежащий множеству, и не
обладает ни один элемент, который ему не
принадлежит.

8.

• перечислить все его элементы,
или
• указать характеристическое
свойство его элементов.

9.

1 способ
(перечисление элементов
множества)
2 способ
(указание характеристического
свойства)
1. Множество квадратов натуральных чисел.
А = {1, 4, 9, 16 …}
А = {n2 / n }
2. Множество четных натуральных чисел.
А = {2, 4, 6, 8 …}
A = {2n / n }
3. Множество решений уравнения
х2 – 5|х|+6 = 0
А = {-3; -2; 2; 3}
А = {х / х2 – 5|х|+6 = 0}

10.

• Множество В называется подмножеством
множества А, если каждый элемент множества
В является так же элементом множества А
• Обозначение: В А
А = { 1, 2, 3, 4, 5, 6, 7, 8, 9 }.
В = { 1, 3, 5, 7, 9 }.
Множество В является подмножеством
множества А.

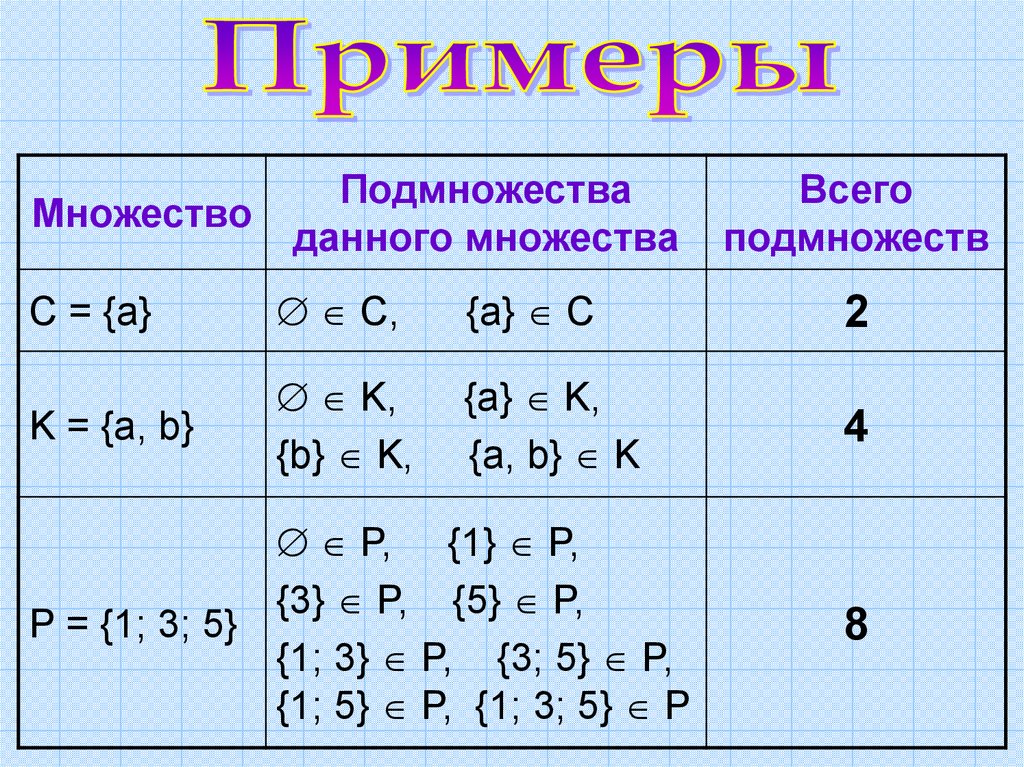
11.

Множество
Подмножества
данного множества
С = {а}
С,
{а} С
2
K = {а, b}
K,
{b} K,
{а} K,
{а, b} K
4
P, {1} P,
{3} P, {5} P,
P = {1; 3; 5}
{1; 3} P, {3; 5} P,
{1; 5} P, {1; 3; 5} P
Всего
подмножеств
8

12.

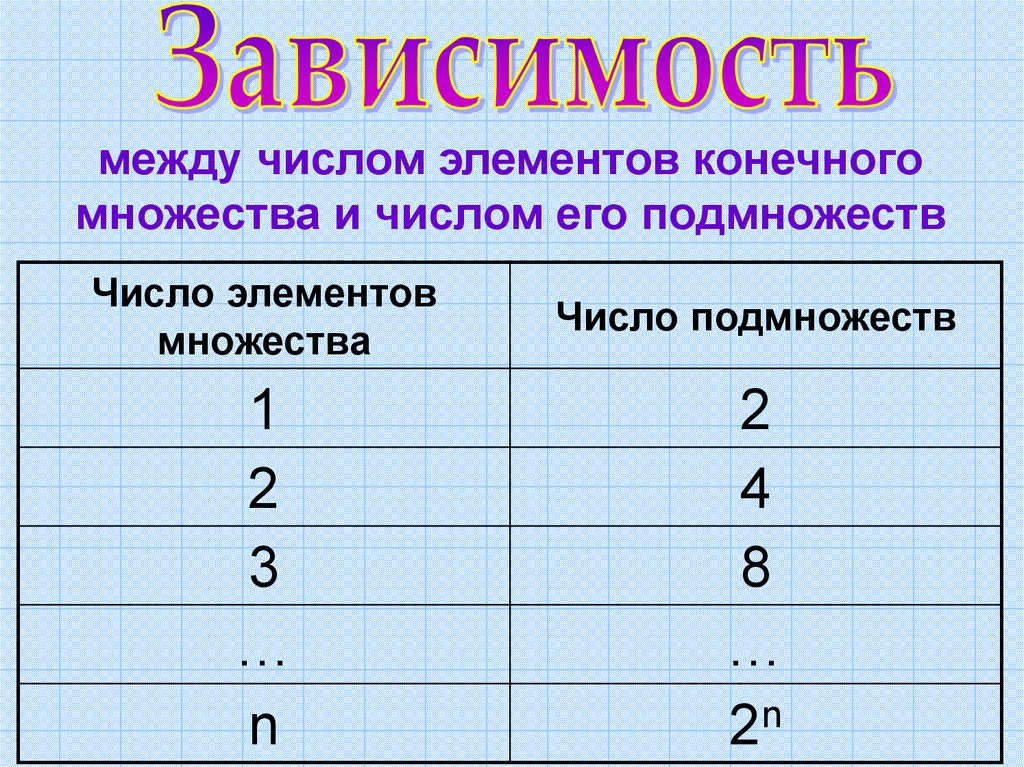
между числом элементов конечного
множества и числом его подмножеств
Число элементов
множества
Число подмножеств
1
2
3
…
n
2
4
8
…
2n

13.

Оказывается, что число подмножеств
множества, состоящего из n элементов,
составляет 2n.

14.

Каждое множество является
подмножеством некоторого множества,
которое называют универсальным. Его
обозначают буквой I. Например,
множество натуральных чисел является
подмножеством множества всех чисел;
множество жителей г. Тамбова является
подмножеством множества жителей
России.

15.

• Множества А и В, состоящие из одних и тех же
элементов, называются равными.
• Обозначение: А = В
• Если относительно двух множеств А и В
установлено, что А В и А В, то это и
означает, что А = В.
Пример:
С – множество чисел, кратных 3 и 5 одновременно
D – множество чисел, кратных 15
С=D

16.

• Пересечением (произведением) двух
множеств А и В называется множество,
состоящие из всех элементов,
принадлежащих одновременно и множеству
А, и множеству В.
• Обозначение: А В
Пример:
A = {2n}; B = {3n + 1}
A B = {6n + 2}

17.

• Объединением (суммой) двух множеств А и В
называется множество, состоящее из всех
элементов, принадлежащих хотя бы одному из
данных множеств А или В.
• Обозначение: А В
Примеры:
1) A = {3k +1}; B = {3k}; C = {3k + 2}, где k
A B C = {3k}
2) A = {ромбы}; B = {параллелограммы}
A B = {ромбы; параллелограммы} =
{параллелограммы}

18.

• Разностью множеств А и В называется
множество, из всех тех элементов
множества А, которые не являются
элементами множества В.
• Обозначение: В’а

19.

• Дополнением множества В до
множества А называется множество,
содержащее только те элементы
множества А, которые не принадлежат
множеству В.
• Обозначение: А\В

20.

действий над множествами
1. А =
2. А I = А
3. А А = А
4. если В А, то А В = В
5. А В = В А
6. А (В С) = (А В) С = С А В
7. (А В) А
8. ’ = I
9. I’ =
10. A = A

21.

действий над множествами
11. A A = A
12. A B = B A
13. A (B C) = (A B) C = A B C
14. A (B C) = (A B) (A C)
15. (A B) C = (A C) (B C)
16. A (A B)
17. если В А, то A B = А
18. если В А, то A B = В
19. (A B)’ = А’ B’
20. (A B)’ = А’ B’

22.

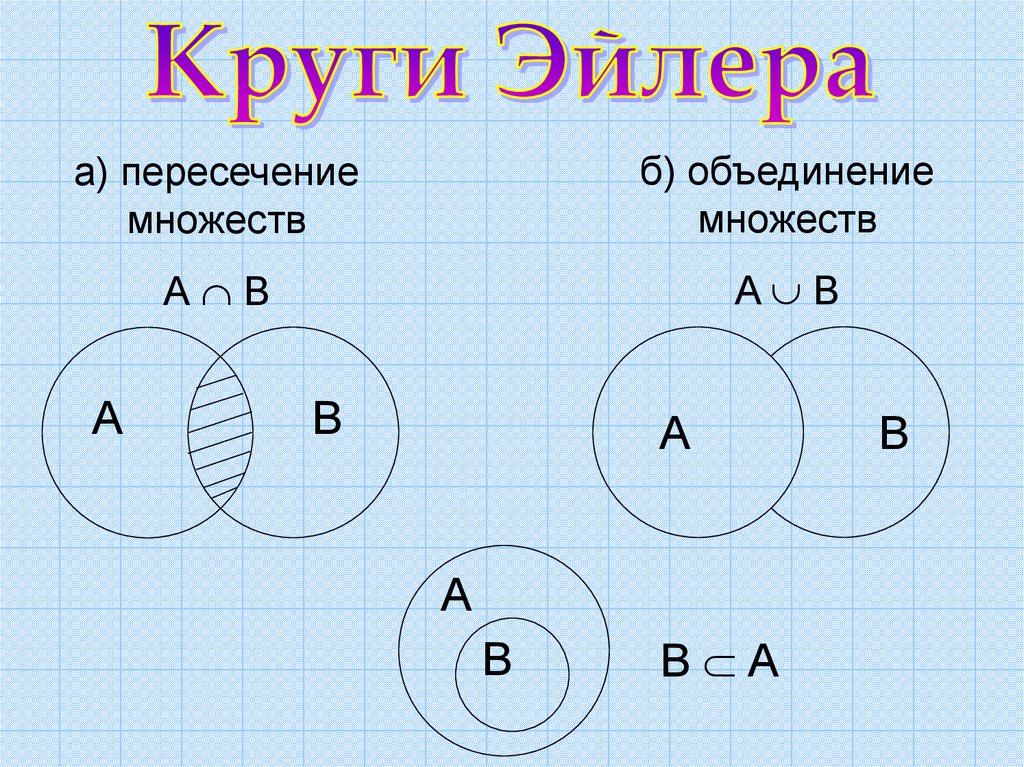
а) пересечение
множеств
б) объединение
множеств
А В
A B
А
В
А
А
В
В А
В

23.

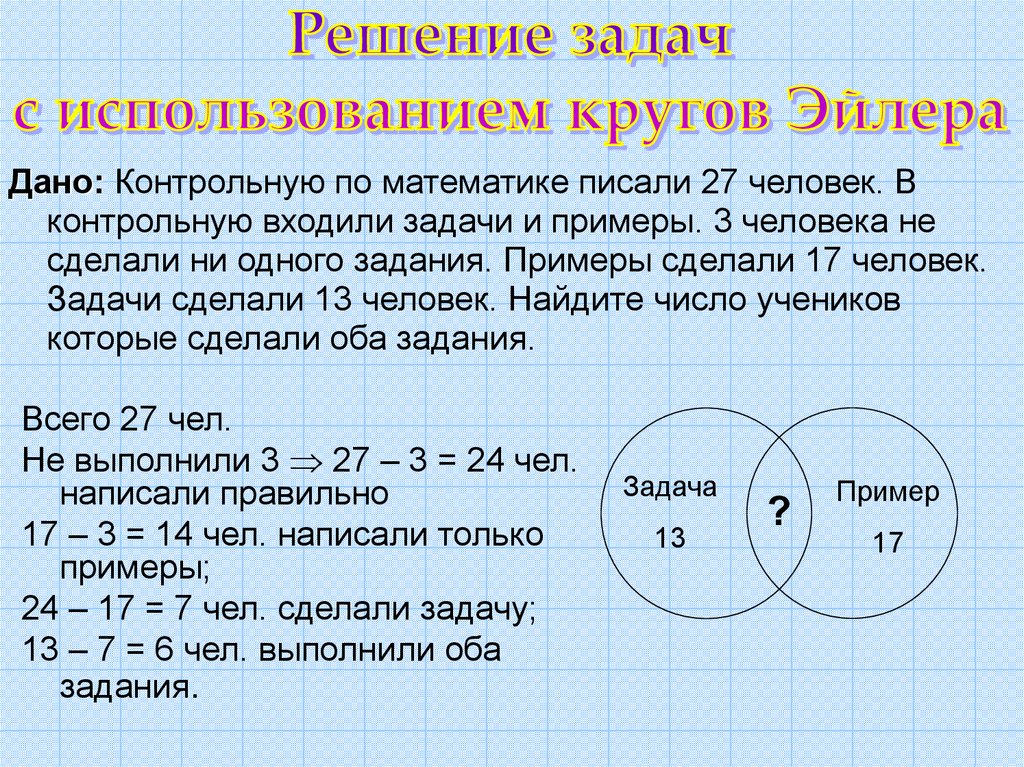
Дано: Контрольную по математике писали 27 человек. В
контрольную входили задачи и примеры. 3 человека не
сделали ни одного задания. Примеры сделали 17 человек.
Задачи сделали 13 человек. Найдите число учеников
которые сделали оба задания.
Всего 27 чел.
Не выполнили 3 27 – 3 = 24 чел.
написали правильно
17 – 3 = 14 чел. написали только
примеры;
24 – 17 = 7 чел. сделали задачу;
13 – 7 = 6 чел. выполнили оба
задания.
Задача
13
?
Пример
17

24.

Дано: В школе изучают английский, французский и немецкий языки.
Английский изучают 235 человек, французский изучают 160 человек,
немецкий изучают 186 человек. Английский и немецкий изучают 90
человек. Немецкий и французский изучают 75 человек. Английский и
французский изучают 112 человек. Все три языка изучают 28 человек.
Всего - ?
Английский язык = 61
Немецкий язык = 49
Французский язык = 1
Англ. яз.
90 Нем. яз.
Англ. яз. + Нем. яз. = 90
235
186
28
Англ. яз. + Франц. яз. = 112
112
75
Франц. яз. + Нем. яз. = 75
Франц. яз. + Нем. яз. + Англ. яз. = 28
Франц. яз.
Всего: 332 человека.
160