Similar presentations:
Индуктивное логическое программирование (ILP)
1. Индуктивное логическое программирование (ILP)
ILP (Inductive Logic Programming) - раздел машинного обучения, которыйиспользует логическое программирование как форму представления примеров,
фоновых знаний и гипотез.
Получив описания уже известных фоновых знаний и набор примеров,
представленных как логическая база фактов, система ILP может породить
логическую программу в форме гипотез, объясняющую все положительные
примеры и ни одного отрицательного.
Фоновые знания – знания, известные ученику до начала обучения.
Схема:
положительные примеры + отрицательные примеры + фоновые знания => гипотезы
Термин «индуктивное логическое программирование» был впервые
использован в статье Стивена Магглтона (Stephen Muggleton) в 1991 году.
Термин «индуктивное» здесь употребляется в философском (предложение
теории для объяснения наблюдаемых фактов), а не в математическом
(доказательство свойства членов множества) смысле.
1
2. Задача ILP
ILP – один из подходов к машинному обучению.Результат обучения – формула логики предикатов, обычно программа Prolog.
При таком подходе машинное обучение - это своего рода автоматическое
программирование, когда разработчик не занимается написанием программ.
Вместо этого он показывает на примерах, для выполнения каких действий
предназначена создаваемая программа.
«+»-примеры – указывают, что должна делать программа.
«-»-примеры – указывают, что эта программа не должна делать.
Кроме этого пользователь задает фоновые предикаты, которые могут
использоваться при написании новой программы.
2
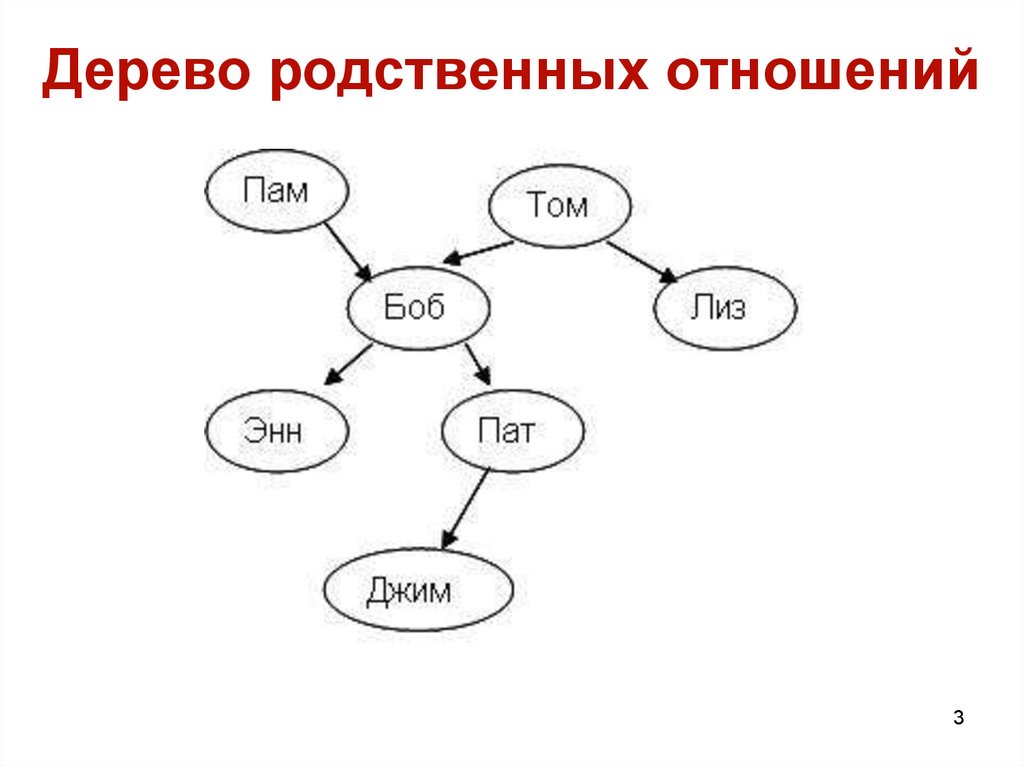
3. Дерево родственных отношений
34. Пример задачи ILP
Предположим, что имеются предикаты:parent(X, Y)
male(X)
female(X)
Необходимо найти определение нового предиката
has_daughter(X)
Даны «+»-примеры:
has_daughter(tom)
has_daughter(bob)
Даны «-»-примеры:
has_daughter(pam)
has_daughter(jim)
Задача – найти определение предиката has_daughter(X) в терминах предикатов
parent, male и female таким образом, чтобы он принимал истинное значение для
всех «+»-примеров и ложное значение для всех «-»-примеров.
4
5. Задача ILP
Приведенный пример демонстрирует типичное отличие такого реляционного(основанного на отношениях) обучения от обучения на основе атрибутов и
значений.
Свойство has_daughter объекта X определено не только в терминах атрибутов
X. Вместо этого для определения наличия у объекта X свойства
has_daughter рассматривается другой объект, Y, связанный с X, и проверяются
свойства объекта Y.
5
6. Терминология ILP
Предикат, который должен быть получен в результате обучения, has_daughter,называется целевым предикатом.
Заданные предикаты parent, male и female называются фоновыми знаниями
(Background Knowledge — ВК), или фоновыми предикатами. Это — знания,
известные ученику до начала обучения.
Фоновые предикаты фактически определяют язык, на котором ученик может
выражать гипотезы, относящиеся к целевому предикату.
6
7. Задача ILP
Дано:1. множество положительных примеров Е+ и множество отрицательных
примеров Е-;
2. фоновые знания ВК, заданные как множество логических формул, такие, что
примеры Е+ невозможно вывести логически из ВК.
Найти:
гипотезу Н, заданную как множество логических формул, такую, что
1. все положительные примеры в Е+ можно вывести логически из ВК и Н;
2, ни одного отрицательного примера в Е- нельзя вывести логически из ВК и Н.
7
8. Задача ILP
Дано:1. множество положительных примеров Е+ и множество отрицательных
примеров Е-;
2. фоновые знания ВК, заданные как множество логических формул, такие, что
примеры Е+ невозможно вывести логически из ВК.
Найти:
гипотезу Н, заданную как множество логических формул, такую, что
1. все положительные примеры в Е+ можно вывести логически из ВК и Н;
2, ни одного отрицательного примера в Е- нельзя вывести логически из ВК и Н.
Н вместе с BК должны охватывать все положительные примеры и не должны
охватывать ни одного из отрицательных примеров. Подобная гипотеза H
называется полной (охватывающей все положительные примеры) и
достоверной (совместимой только с положительными примерами, т.е. не
охватывающей ни одного отрицательного примера).
8
9. Задача ILP
Обычно ВК и Н представляют собой множества предложений Prolog-программы.Поэтому с точки зрения автоматического программирования на языке Prolog
приведенная выше формулировка задачи обучения соответствует следующей.
Предположим, что целевым предикатом является р (X) и кроме
прочих примеров имеются некоторые положительный пример р(а) и
отрицательный пример р(b).
Возможный диалог с программой ВК может состоять в следующем:
? р(а) . % Положительный пример
nо % Не может быть выведен логически из ВК
? p(b) . % Отрицательный пример
nо % Не может быть выведен логически из ВК
Теперь предположим, что вызвана на выполнение система ILP, которая
автоматически осуществляет логический вывод дополнительного множества
предложений Н и добавляет их к программе BK.
9
10. Задача ILP
После этого возможный диалог с расширенной таким образом программой,состоящей из предложений ВК и Н, может представлять собой следующее:
? р(а). % Положительный призер
yes % Может быть выведен логически из BК и Н
? р(b). % Отрицательный пример
nо % Не может быть выведен логически из ВК и Н
Широко известные задачи в области ILP: автоматическое формирование
программ Prolog для конкатенации или сортировки списков. Такие программы
создаются на основании положительных примеров того, как должна
осуществляться конкатенация или сортировка списков, а также отрицательных
примеров того, как эти действия не должны выполняться.
10
11. Определение задачи изучения предиката has_daughter
% Изучение предиката по фактам, определяющим семейные отношения% Фоновые знания
backliteral( parent(X,Y), [X,Y]). % Фоновый литерал с переменными [X,Y]
backliteral(male(X), [X]).
% 2-й аргумент – список переменных
backliteral( female(X), [X]).
prolog_predicate( parent(_,_)). % Цель parent(_,_) выполняется
% непосредственно интерпретатором Prolog
prolog_predicate( male(_)).
prolog_predicate( female(_)).
parent( pam, bob).
parent( torn, bob).
parent( torn, liz).
parent( bob, ann).
parent( bob, pat) .
parent( pat, jim).
parent( pat, eve).
11
12. Определение задачи изучения предиката has_daughter
female( pam).female( liz).
female( ann).
female( pat).
female( eve).
male( tom).
male( bob).
male( jim).
% Положительные примеры
ex( has_daughter(tom)). % Том имеет дочь
ex( has_daughter(bob)).
ex( has_daughter(pat)).
% Отрицательные примеры
nex( has_daughter(pam)). % Пэм не имеет дочери
nex( has_daughter(jim)).
start_hyp( [ [has_daughter(X)] / [X] ] ). % Начальная гипотеза
12
13. Граф усовершенствования
Можно начать с некоторой слишком общей гипотезы, которая является полной(охватывает все положительные примеры), но несовместимой (не охватывает
лишь положительные примеры, т.е. охватывает также отрицательные примеры).
Подобная гипотеза должна быть усовершенствована таким образом,
чтобы она сохранила свою полноту и стала совместимой. Этого можно достичь
путем поиска в пространстве возможных гипотез и их усовершенствований. При
каждом усовершенствовании берется гипотеза H1 и вырабатывается более
конкретная гипотеза Н2 такая, что H2 охватывает подмножество случаев,
охватываемых гипотезой H1.
Подобное пространство гипотез и их усовершенствований называется графом
усовершенствования.
Узлы в графе - гипотезы, а дуги между гипотезами - усовершенствования.
Между гипотезами H1 и Н2 имеется ориентированная дуга, если Н2 является
усовершенствованием H1.
13
14. Граф усовершенствования
После определения графа усовершенствования задача обучения сводится кпоиску в этом графе.
Начальный узел поиска - некоторая слишком общая гипотеза.
Целевой узел поиска - совместимая и полная гипотеза.
В примере достаточно, чтобы все гипотезы представляли собой отдельные
предложения, но в общем гипотезы могут состоять из нескольких предложений.
Для реализации описанного подхода необходимо разработать два компонента.
1. Оператор усовершенствования, который будет вырабатывать
усовершенствования гипотез (такой оператор определяет граф
усовершенствования).
2. Процедура поиска для выполнения поиска.
14
15. Граф усовершенствования
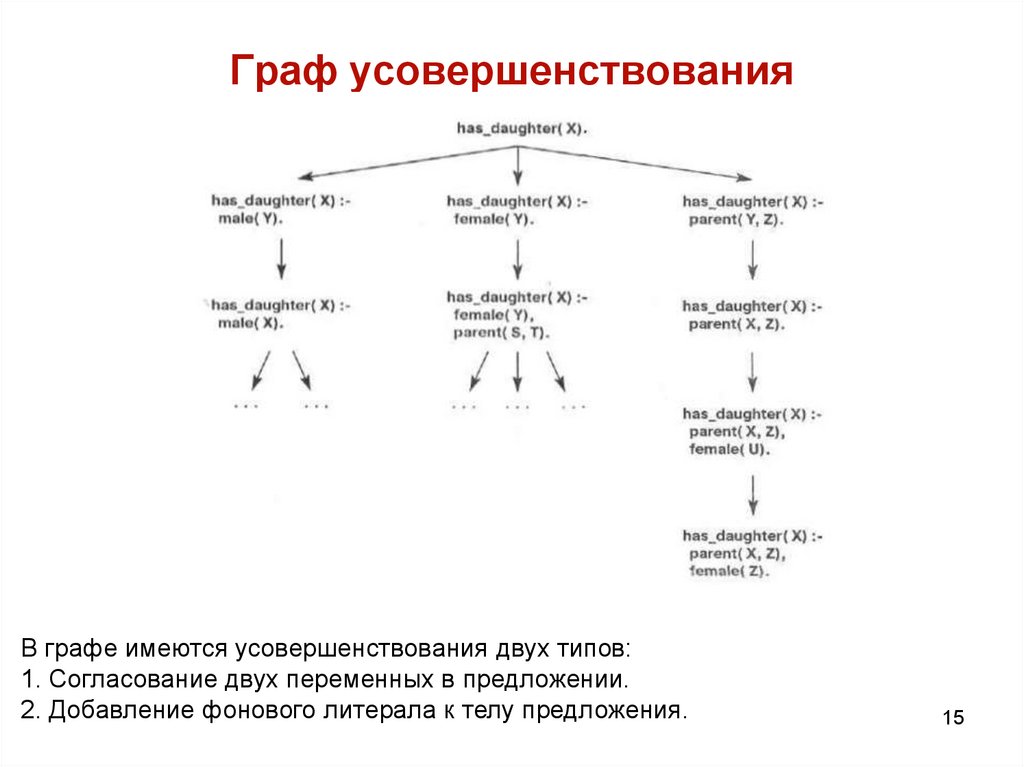
В графе имеются усовершенствования двух типов:1. Согласование двух переменных в предложении.
2. Добавление фонового литерала к телу предложения.
15
16. Граф усовершенствования
Пример усовершенствования 1 типа:has_daughter(X) :- patent(Y, Z).
Это предложение путем усовершенствования преобразуется в предложение
has_daughter(X) :- parent(X, Z).
в котором выполнено согласование X=Y.
Примером усовершенствования 2 типа:
has_daughter(X).
путем усовершенствования преобразуется в следующее предложение:
has_daughter(X) :- parent(Y, Z).
16
17. Граф усовершенствования
Особенности усовершенствований1. Каждое усовершенствование представляет собой уточнение. Преемник
любой гипотезы в графе усовершенствования охватывает лишь некоторое
подмножество тех случаев, которые охвачены предшественником этой гипотезы.
Поэтому в процессе поиска достаточно рассматривать только полные гипотезы
(которые охватывают все положительные примеры). Неполная гипотеза в
процессе усовершенствования не может стать полной.
2. Оператор усовершенствования должен осуществлять достаточно "малые"
этапы усовершенствования. В противном случае оператор усовершенствования
может не позволить выработать целевую гипотезу. Оператор, допускающий
слишком крупные этапы усовершенствования, может перейти от полной и
несовместимой гипотезы прямо к неполной и совместимой, минуя находящуюся
между ними совместимую и полную гипотезу.
3. Может рассматриваться еще один тип усовершенствования, который
предусматривает замену переменных структурированными термами:
member(X1, L1) :- member(X1, L3) .
может быть преобразовано в процессе усовершенствования в
member(X1, [Х2 | L2]) :- member(X1, L3).
В результате усовершенствования переменная L1 преобразуется
в структуру [Х2 | L2].
17
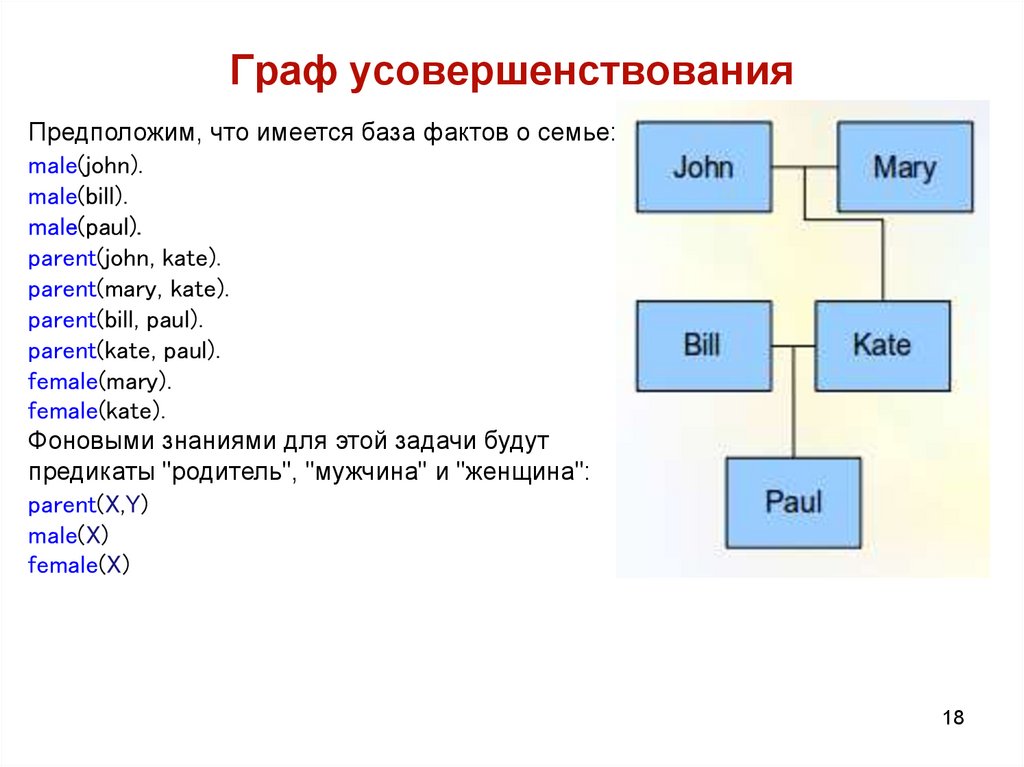
18. Граф усовершенствования
Предположим, что имеется база фактов о семье:male(john).
male(bill).
male(paul).
parent(john, kate).
parent(mary, kate).
parent(bill, paul).
parent(kate, paul).
female(mary).
female(kate).
Фоновыми знаниями для этой задачи будут
предикаты "родитель", "мужчина" и "женщина":
parent(X,Y)
male(X)
female(X)
18
19. Граф усовершенствования
Мы хотим научить ILP-систему предикату "имеет дочь".Определим его как целевой предикат:
has_daughter(X)
Для этого предиката положительные примеры будут:
has_daughter(mary)
has_daughter(john)
Отрицательные примеры:
has_daughter(bill)
has_daughter(kate)
has_daughter(paul)
19
20. Граф усовершенствования
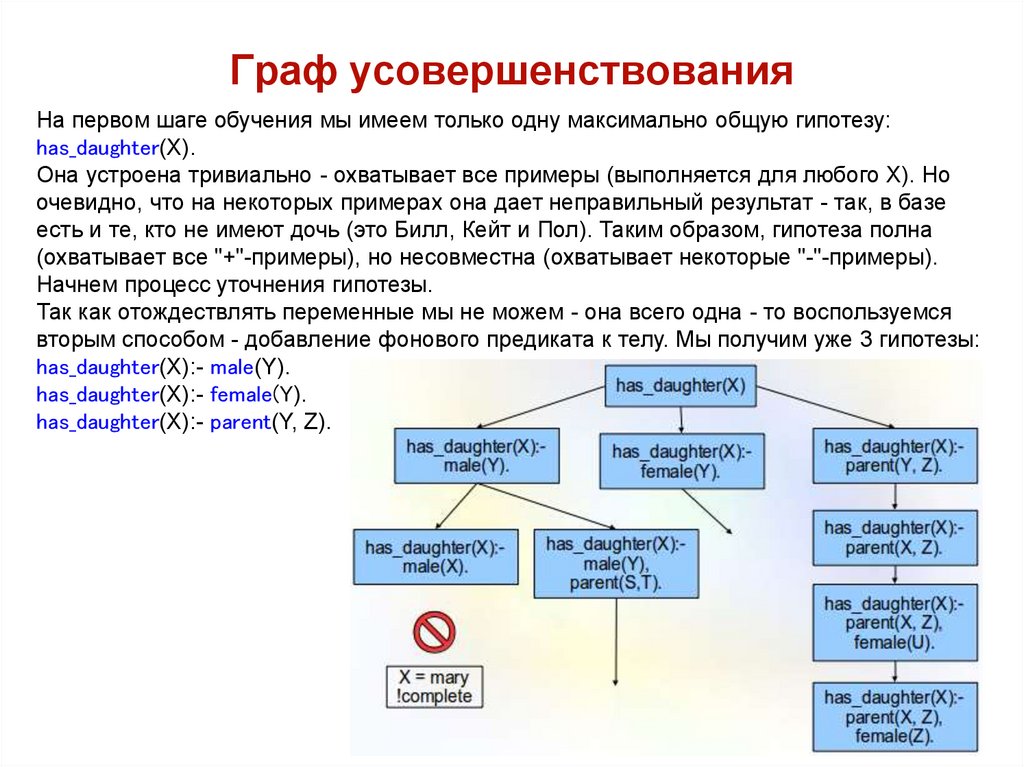
На первом шаге обучения мы имеем только одну максимально общую гипотезу:has_daughter(X).
Она устроена тривиально - охватывает все примеры (выполняется для любого X). Но
очевидно, что на некоторых примерах она дает неправильный результат - так, в базе
есть и те, кто не имеют дочь (это Билл, Кейт и Пол). Таким образом, гипотеза полна
(охватывает все "+"-примеры), но несовместна (охватывает некоторые "-"-примеры).
Начнем процесс уточнения гипотезы.
Так как отождествлять переменные мы не можем - она всего одна - то воспользуемся
вторым способом - добавление фонового предиката к телу. Мы получим уже 3 гипотезы:
has_daughter(X):- male(Y).
has_daughter(X):- female(Y).
has_daughter(X):- parent(Y, Z).
20
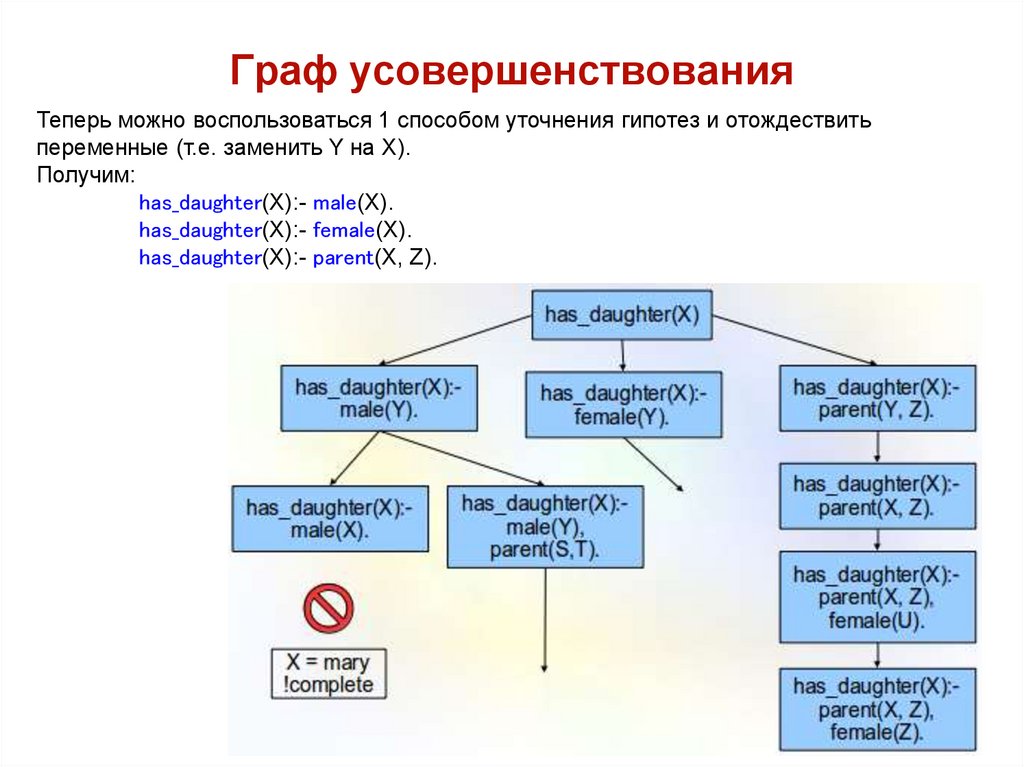
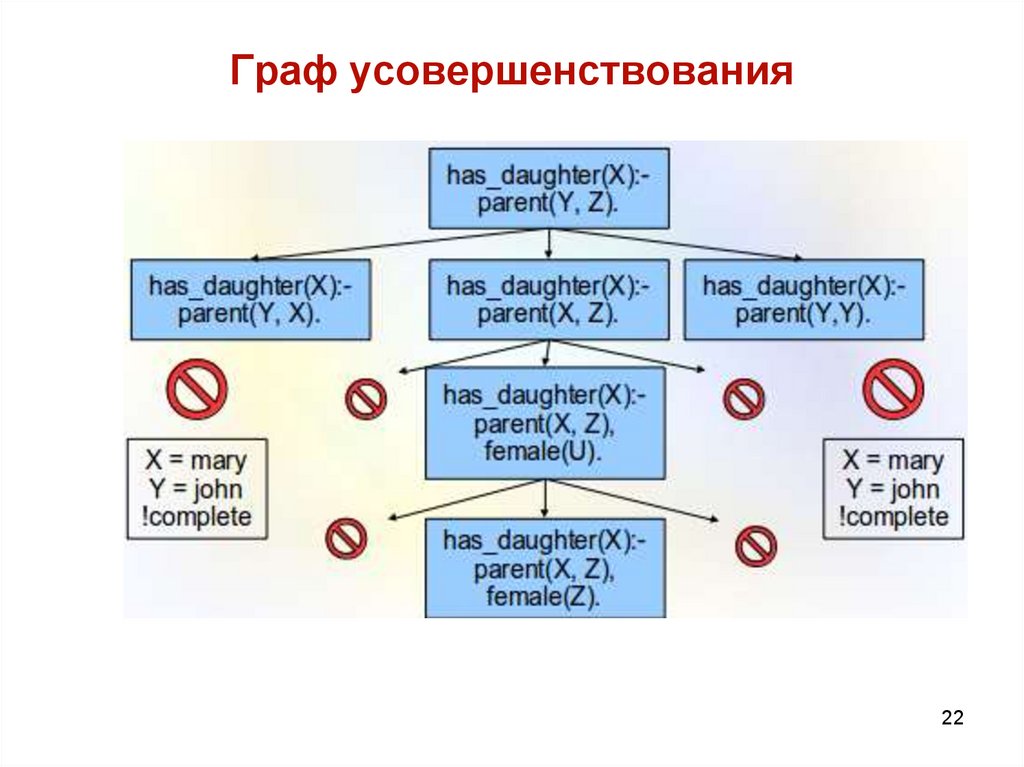
21. Граф усовершенствования
Теперь можно воспользоваться 1 способом уточнения гипотез и отождествитьпеременные (т.е. заменить Y на X).
Получим:
has_daughter(X):- male(X).
has_daughter(X):- female(X).
has_daughter(X):- parent(X, Z).
21
22. Граф усовершенствования
2223. ILP
Возможности:• Обучение рекурсивным понятиям, таким как "потомок".
• Мультипредикатное обучение (одновременное изучение нескольких предикатов, когда
один предикат определяется в терминах другого).
Недостатки:
• Требуется вручную указать количество и тип переменных в целевом предикате.
• Высокая вычислительная сложность (NP-полная задача). При добавлении литералов
увеличивается число переменных в предикате. Любое подмножество переменных
может быть отождествлено между собой, что сразу дает экспоненциальный рост
сложности.
Эвристики:
Возможные ограничения для уменьшения временных затрат:
• Ограничение на максимальную глубину поиска
• Ограничение на максимальное число литералов в теле предиката
• Введение параметра "стоимость гипотезы":
Cost(H) = количество_переменных(H) + 10*количество_литералов(H) + 10*NegCover(H)
23

















 programming
programming








