Similar presentations:
Закони розподілу. Лекція 8
1. ЗАКОНИ РОЗПОДІЛУ
План1. Параметричні критерії.
2. t-критерій Стьюдента (t-розподіл)
2. t-критерій Стьюдента (t-розподіл)
В 1908 р. математик В. Госсет (що друкувався під псевдонімомСтьюдент), знайшов закон розподілу величини t x
/ n
, в якій генеральний параметр замінений на його вибіркову
характеристику sx, тобто Стьюдент знайшов закон розподілу значень
t
x
s/ n
Відкритий Стьюдентом і теоретично обгрунтований Р. Фішером закон
t-розподілу слугує основою так званої теорії малої вибірки, яка
характеризує розподіл вибіркових середніх в сукупності, що
нормально розподіляється, залежно від об'єму вибірки, t-розподіл
залежить лише від числа ступенів свободи до k = n – 1, причому із
збільшенням об'єму вибірки n t-розподіл швидко наближається до
нормального з параметрами = 0 і =1 і вже при n 30 не
відрізняється від нього.
3.
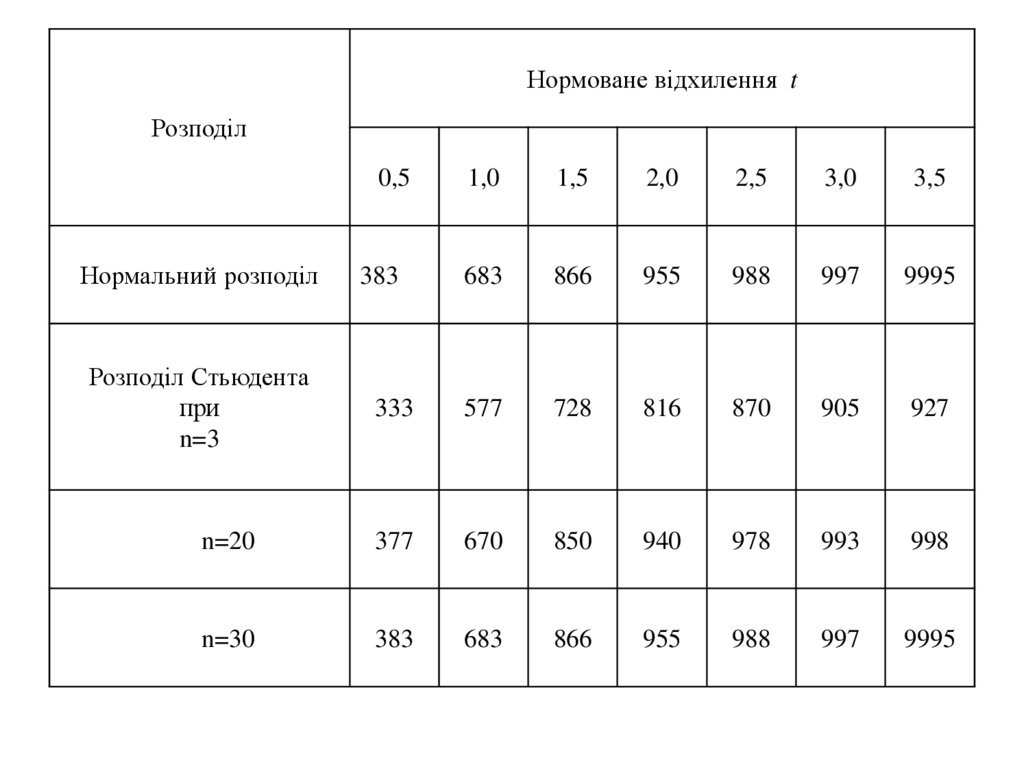
Нормоване відхилення tРозподіл
0,5
1,0
1,5
2,0
2,5
3,0
3,5
Нормальний розподіл
383
683
866
955
988
997
9995
Розподіл Стьюдента
при
n=3
333
577
728
816
870
905
927
n=20
377
670
850
940
978
993
998
n=30
383
683
866
955
988
997
9995
4.
Наочніше уявлення про характер t-розподілy дає малюнок, наякому на фоні нормальної кривої зображена (пологіша) крива tрозподілy при n=3. t-розподіл симетричний і відображає
специфіку розподілу середньої арифметичної у разі малої
вибірки залежно від її об'єму (n). Для вибірок, об'єм яких
перевищує 30 одиниць, величина t розподіляється нормально і
не залежить від числа спостережень. Якщо ж n<30, характер tрозподілy знаходиться залежно від числа спостережень n.
5. Оцінка різниці середніх
Порівнюючи між собою дві незалежні вибірки, узяті з тих, щонормально розподіляються сукупностей з параметрами 1 і, 2 можна
2
припустити, що 1 2 D а дисперсія цієї різниці D . Значення
генеральних параметрів невідомі, проте нескладно знайти величини
вибіркових середніх і різницю між ними ( x1 x2 ) d. Нульова гіпотеза
зводиться до припущення, що 1 2 .
Критерієм для перевірки Н0-гіпотези є відношення
( x1 x 2 ) ( 1 2 )
t
s x1 x2
де t — змінна величина, що йде за t-розподілом Стьюдента з числом
ступенів свободи k=(n1—1)+ (n2—1) = n1+ n2—2, а
s x1 x2
— похибка вказаної різниці, що позначається надалі символом Sd.
6.
Оскільки, згідно Н0-гіпотезі, 1 2 0 , то t-критерий виражається увигляді відношення різниці вибіркових середніх до своєї похибки, тобто
x1 x2
d
t
sd
sd
Н0-гіпотезу відкидають, якщо фактично встановлена величина t-критерію
(що позначається символом tф) перевершить або виявиться рівною
критичному (стандартному) значенню tst цієї величини для прийнятого
рівня значущості а і числа ступенів свободи k = n1 + n2—2, тобто за умови
t ф t st
Похибку різниці середніх sd визначають по наступних формулах:
а) для рівночисельних вибірок, тобто при n1 = n2,
(x x )
(x x )
(x x ) (x x )
s s s
2
d
2
x1
2
x2
i
1
n(n 1)
2
i
2
n(n 1)
2
i
1
(n 1)n
i
2
2
7.
б) для нерівночисельних вибірок, тобто при n1 n2(n1 1) s12 (n2 1) s 22 n1 n2
sd
(
)
n1 n2 2
n1n2
2
2
(
x
x
)
(
x
x
)
i 1 i 2 ( n1 n2 )
n1 n2 2
n1n2
1
1
n1 n2
(
)
) можна використовувати
У цій формулі замість (
n1 n2
n1 n2
Приклад 1. Вивчали вплив кобальту на масу тіла кроликів. Дослід
проводили на двох групах тварин: дослідній і контрольної. Були
досліджені кролики у віці від півтора до двох місяців, масою тіла
500—600 гр. Дослід продовжувався півтора місяці. Тваринних обох
груп тримали на одному і тому ж кормовому раціоні. Проте
піддослідні кролики на відміну від контрольних щодня одержували
добавку до раціону у вигляді водного розчину по 0,06 г хлористого
кобальту на 1 кг живої маси тіла. За час досліду тварини дали
наступні надбавки живої маси тіла.
8.
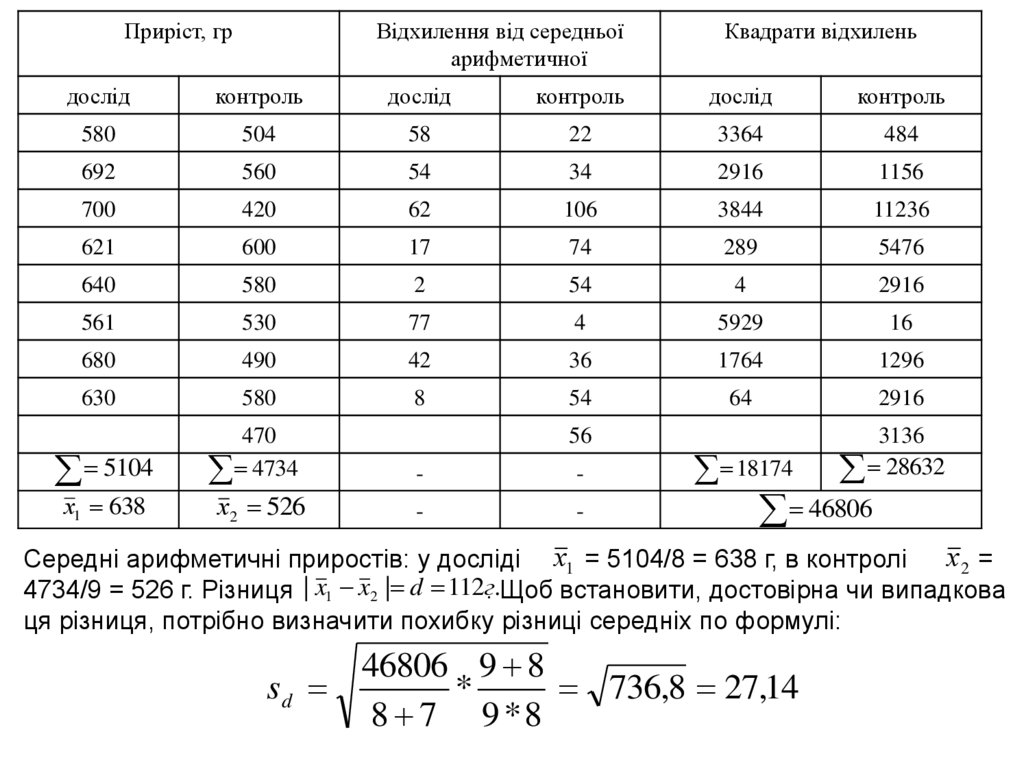
Приріст, грВідхилення від середньої
арифметичної
Квадрати відхилень
дослід
контроль
дослід
контроль
дослід
контроль
580
504
58
22
3364
484
692
560
54
34
2916
1156
700
420
62
106
3844
11236
621
600
17
74
289
5476
640
580
2
54
4
2916
561
530
77
4
5929
16
680
490
42
36
1764
1296
630
580
8
54
64
2916
5104
470
4734
х1 638
х2 526
56
-
-
-
-
18174
3136
28632
46806
х2 =
Середні арифметичні приростів: у досліді х1 = 5104/8 = 638 г, в контролі
4734/9 = 526 г. Різниця | x1 x2 | d 112г. .Щоб встановити, достовірна чи випадкова
ця різниця, потрібно визначити похибку різниці середніх по формулі:
46806 9 8
sd
*
736,8 27,14
8 7 9 *8
9.
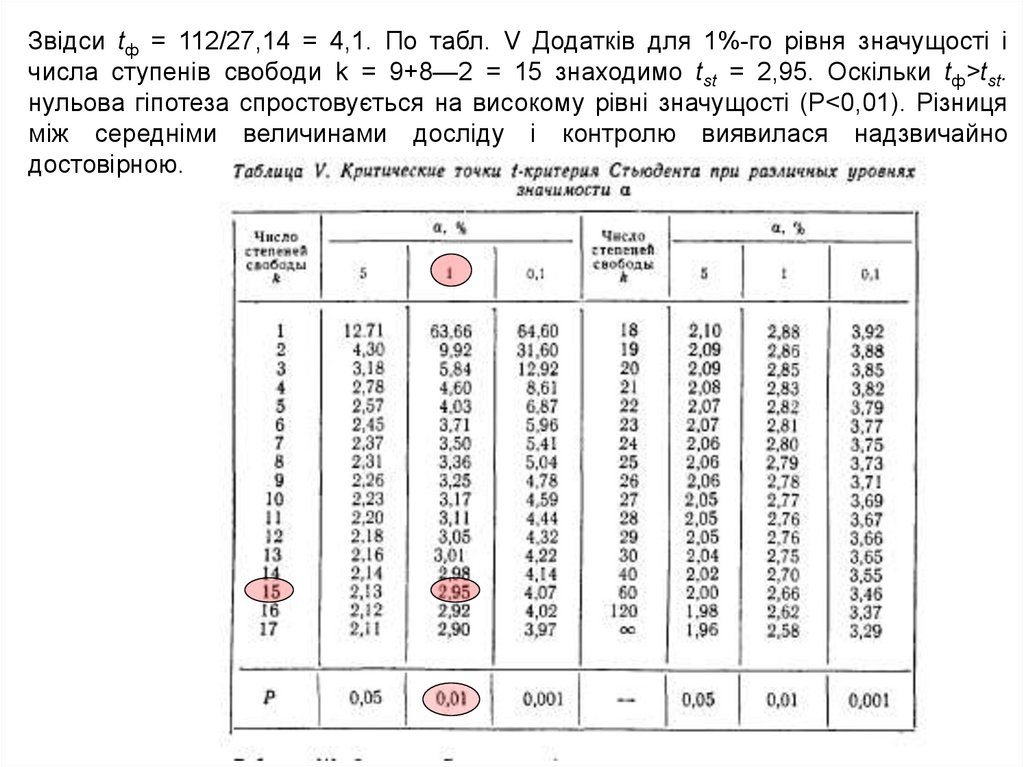
Звідси tф = 112/27,14 = 4,1. По табл. V Додатків для 1%-го рівня значущості ічисла ступенів свободи k = 9+8—2 = 15 знаходимо tst = 2,95. Оскільки tф>tst.
нульова гіпотеза спростовується на високому рівні значущості (Р<0,01). Різниця
між середніми величинами досліду і контролю виявилася надзвичайно
достовірною.
10.
Приклад 2. На двох групах лабораторних мишей — дослідній (n = 9) іконтрольної (n = 11) — досліджували вплив на організм нового
препарату. Після місячних випробувань маса тіла тварин, виражена в
грамах, варіювала таким чином:
У дослідній групі
80, 76, 75, 64, 70, 68, 72, 79, 83
У контрольній групі 70, 78, 60, 80, 62, 68, 73, 60, 71, 66, 69
х1 =74,1
х 2 =68,8
Різниця між середніми | x1 x2 | 5,3г. . Для визначення похибки цієї
різниці заздалегідь розрахуємо девіати:
D1 ( xi x )2 x 2 ( x)2 / n (802 762 ... 832 ) 6672 / 9 302,89 та
D2 (70 2 78 2 60 2 ... 69 2 ) 757 2 / 11 443,64
Звідси похибка різниці середніх виразиться величиною
s d2
302,89 443,64 9 11 14930,6
(
)
8,38
9 11 2
9 *11
1782,0
та
sd 8,38 2,89
11.
Критерій tф = 5,30/2,89=1,83. Для k = 9+11—2=18 та 5%-го рівня значущостів табл. V Додатків знаходимо tst = 2,10. Оскільки tф < tst, нульова гіпотеза
залишається у силі.
12. Оцінка середньої різниці між вибірками з попарно зв'язаними варіантами.
Порівнювані вибірки нерідко є рядами попарно зв'язаних варіант,тобто є залежними вибірками. У таких випадках оцінкою різниці між
генеральними вибірками 1 2 D
буде середня різниця, що
визначається з суми різниць між попарно зв'язаними варіантами
порівнюваних груп, тобто
d
d
i
n
Оцінкою генеральної дисперсії 2 різниці середніх 1 2 D буде
вибіркова дисперсія
(d d ) 2
s2
1
n 1
У даних формулах: n — число парних спостережень; di=xi-yi; d
величина ідентична різниці середніх, тобто
d
d
(x x )
i
n
1
2
13.
Помилку середньої різницівизначають по формулі
d
, що позначається символом sd
2
1 di
sd
(
d2)
n
n
Якщо члени генеральної сукупності розподіляються нормально,
то і різниці між ними розподілятимуться нормально і випадкова
величина t=(d—D)/sd матиме розподіл Стьюдента з k = n—1
ступенями свободи. H0-гiпотеза зводиться до припущення, що
.
1 2 D 0
Звідси t-критерий виразиться у вигляді відношення середньої
t ф t st
різниці до своєї помилки, тобто t=d/sd. Якщо
для
прийнятого рівня значущості і числа ступенів свободи k= n—1, то
нульова гіпотеза повинна бути знехтувана.
14.
Приклад. Впродовж ряду років в умовах Одеської дослідноїстанції вивчали вплив чорного та квітневого пару на врожай
жита. Результати досліду враховували по масі 1000 зерен.
Маса 1000 зерен по рокам досліду
1998
1999
2000
2001
2002
2003
Середні
показники
Квітневий
31,6
24,2
24,8
29,1
29,9
31,0
28,43
Чорний
31,1
24,0
24,6
28,6
29,1
30,1
27,91
Різниця di
0,5
0,2
0,2
0,5
0,8
0,9
d=0,52
Квадрат різниці
di 2
0,25
0,04
0,04
0,25
0,64
0,81
d 2,03
Посів на пару
2
i
З таблиці видно, що врожай жита по квітневому пару дещо
вищий, ніж по чорному.
Середня різницяd di / n 3,1 / 6 0,52 г.
Визначаємо помилку цієї різниці:
sd
1 2,03
0,34 0,27
2
(
0
,
52
)
0,014 0,12
5 6
5
15.
Критерій tф0,52
4,33 . Для к = 6 – 1= 5 та а=1% = 4,03
0,12
Оскільки tф>tst, то Н0-гипотезу tst=4,03 відкидають на високому
рівні значущості (0,001<Р<0,01).
Отже, з ймовірністю Р>0,99 можна стверджувати, що різниця
між порівнюваними вибірками статистично достовірна.












 mathematics
mathematics








