Similar presentations:
Призма. Тема 2
1.
2.
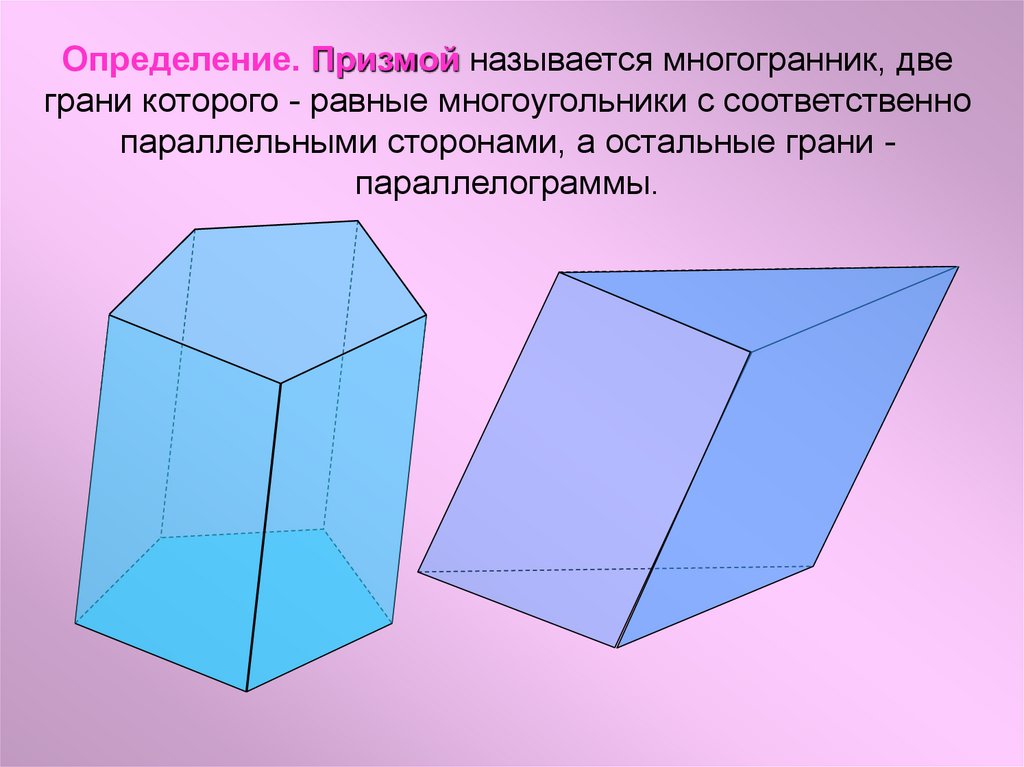
Определение. Призмой называется многогранник, двеграни которого - равные многоугольники с соответственно
параллельными сторонами, а остальные грани параллелограммы.
3.
Два равных многоугольниканазываются основаниями, а
остальные грани - боковыми
гранями
основание
боковая
грань
Отрезки, соединяющие соответствующие вершины оснований, называются боковыми
ребрами
Призма с n-угольником в
основании
называется
n-угольной.
Она имеет n + 2 грани, 2n
вершин и 3n ребер
4.
Основныесвойства призмы
Bn
B1
B3
B2
Основания призмы лежат
в параллельных плоскостях
Боковые ребра равны и
параллельны
Аn
А1
А3
А2
5.
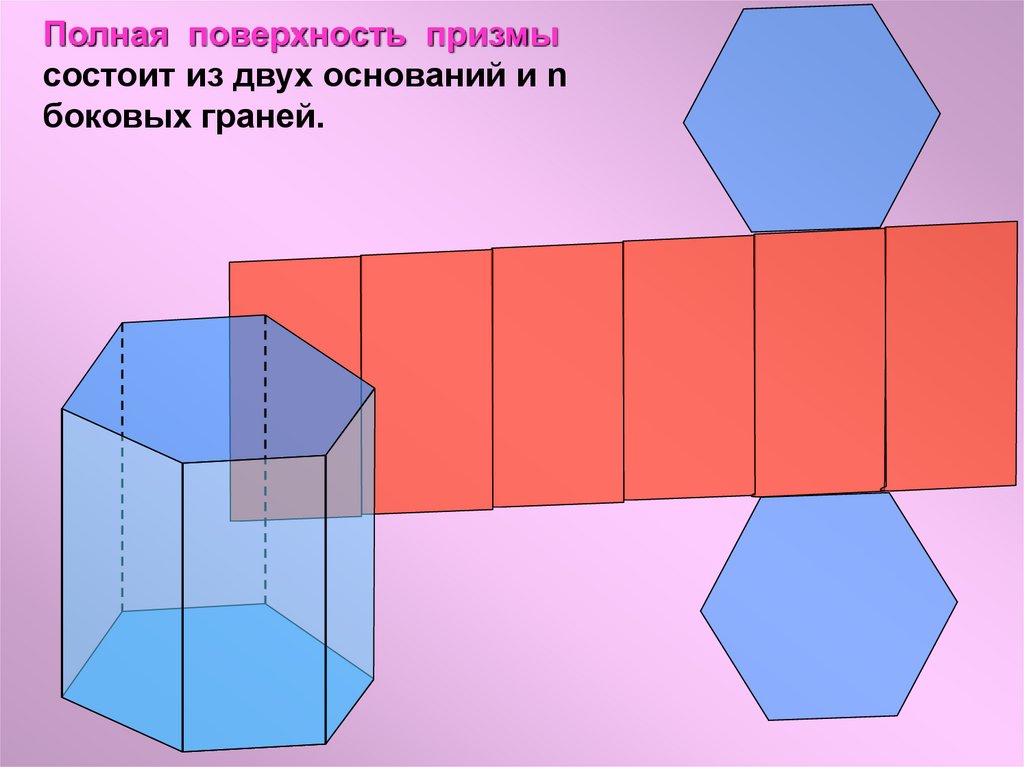
Полная поверхность призмысостоит из двух оснований и n
боковых граней.
6.
BnB1
B3
B2
Аn
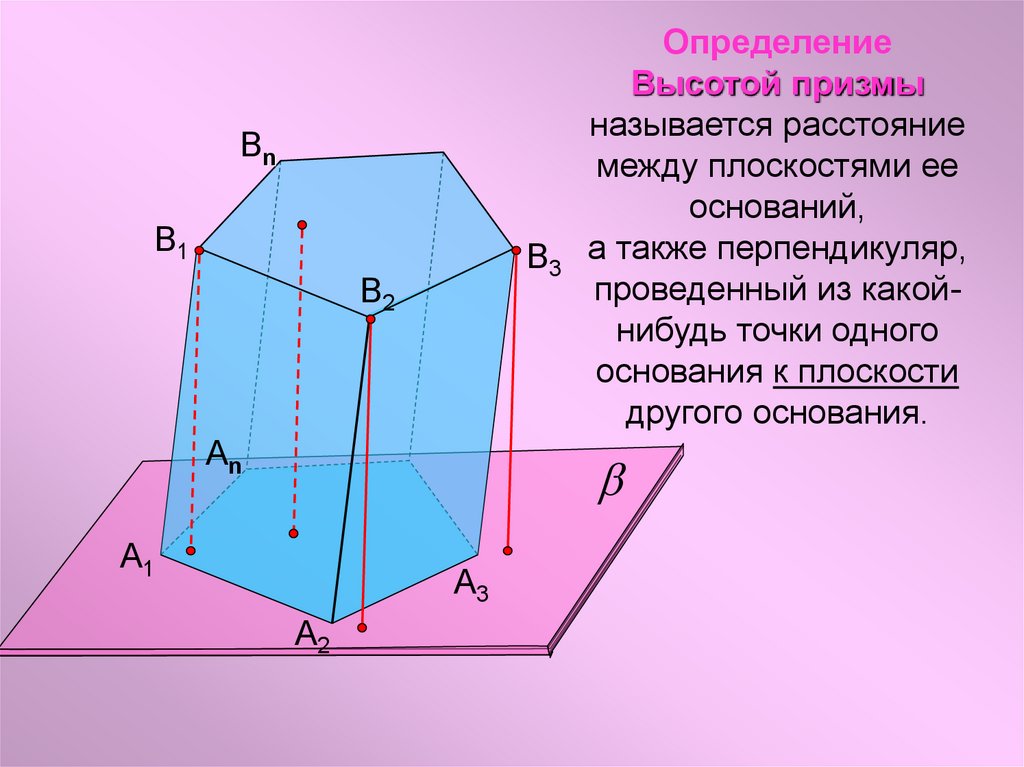
Определение
Высотой призмы
называется расстояние
между плоскостями ее
оснований,
а также перпендикуляр,
проведенный из какойнибудь точки одного
основания к плоскости
другого основания.
А1
А3
А2
7.
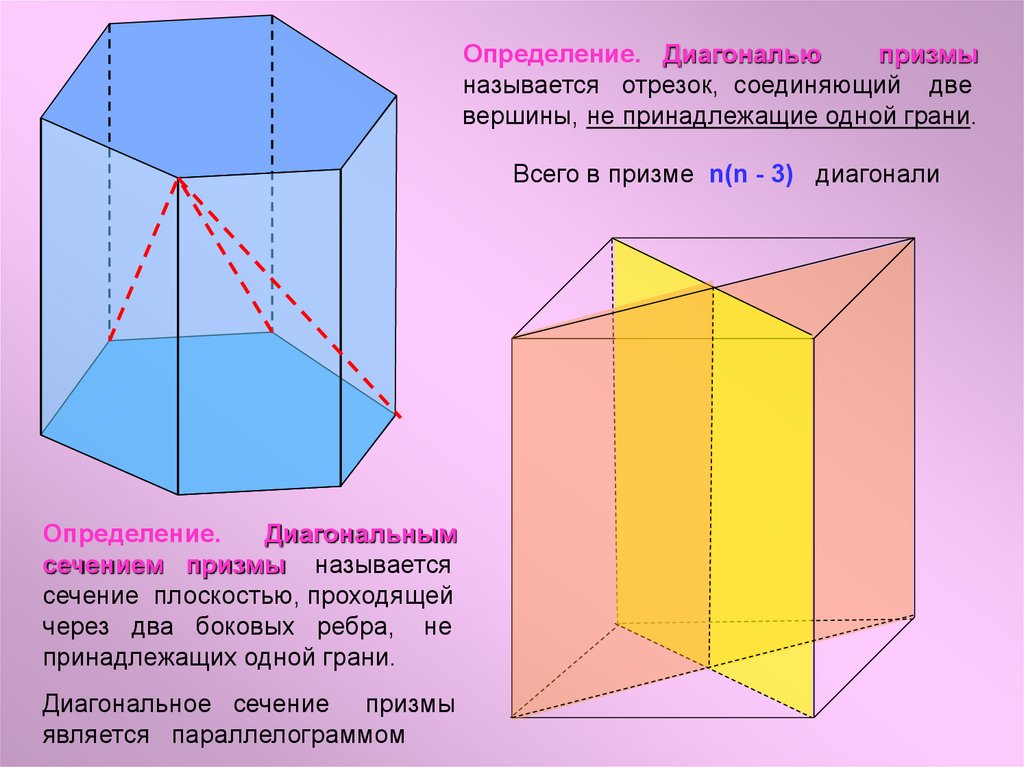
Определение. Диагональюпризмы
называется отрезок, соединяющий две
вершины, не принадлежащие одной грани.
Всего в призме n(n - 3) диагонали
Определение.
Диагональным
сечением призмы называется
сечение плоскостью, проходящей
через два боковых ребра, не
принадлежащих одной грани.
Диагональное сечение призмы
является параллелограммом
8.
Определение.Призматической
поверхностью называется
поверхность, состоящая из
прямых, содержащих боковые
ребра призмы и частей
плоскостей боковых граней,
заключенных между этими
прямыми
9.
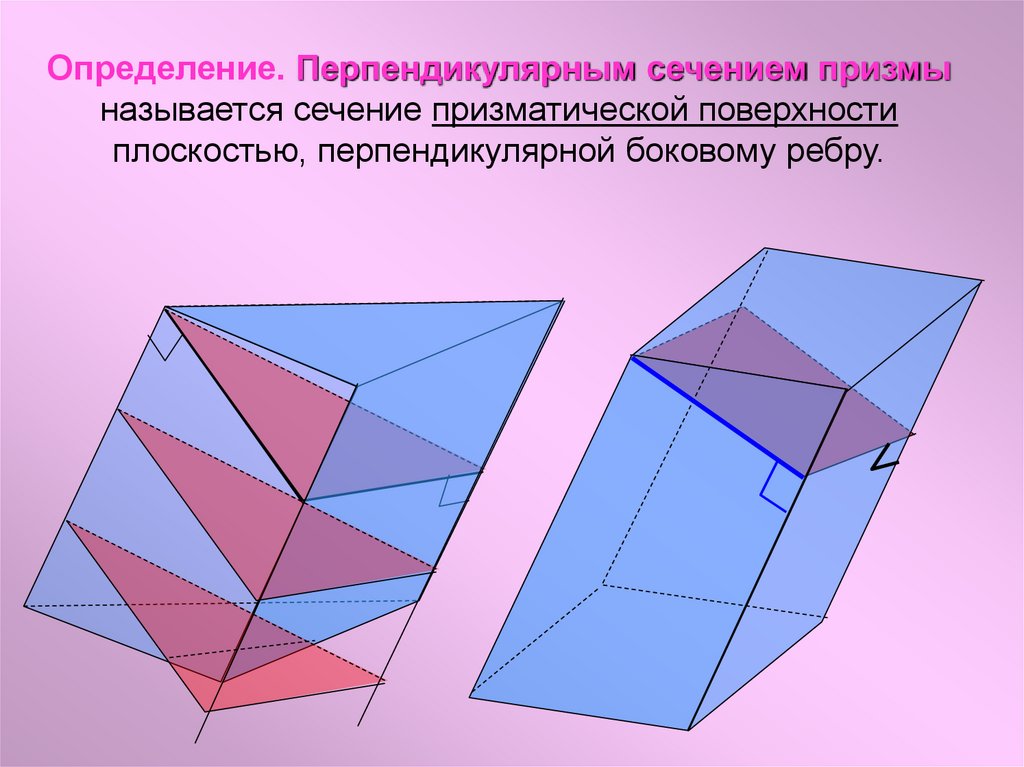
Определение. Перпендикулярным сечением призмыназывается сечение призматической поверхности
плоскостью, перпендикулярной боковому ребру.
10.
Определение. Призма называется прямой, если ее боковыеребра перпендикулярны плоскости основания.
В противном случае призма называется наклонной. В
наклонной призме длина бокового ребра всегда больше
высоты.
11.
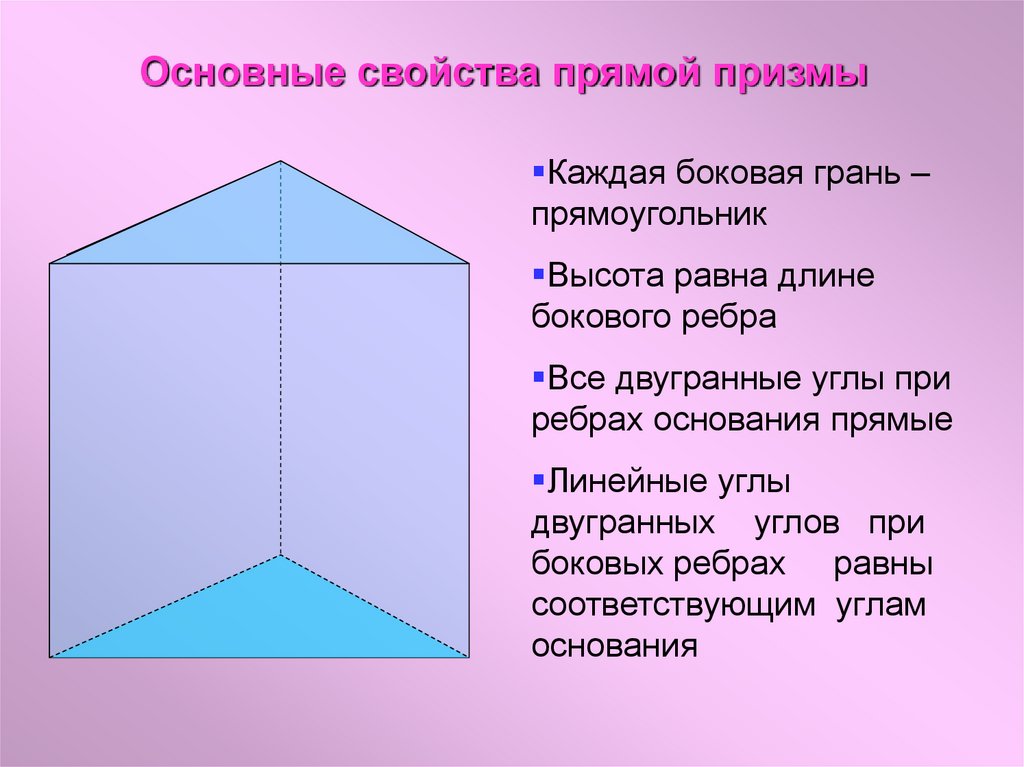
Основные свойства прямой призмыКаждая боковая грань –
прямоугольник
Высота равна длине
бокового ребра
Все двугранные углы при
ребрах основания прямые
Линейные углы
двугранных углов при
боковых ребрах равны
соответствующим углам
основания
12.
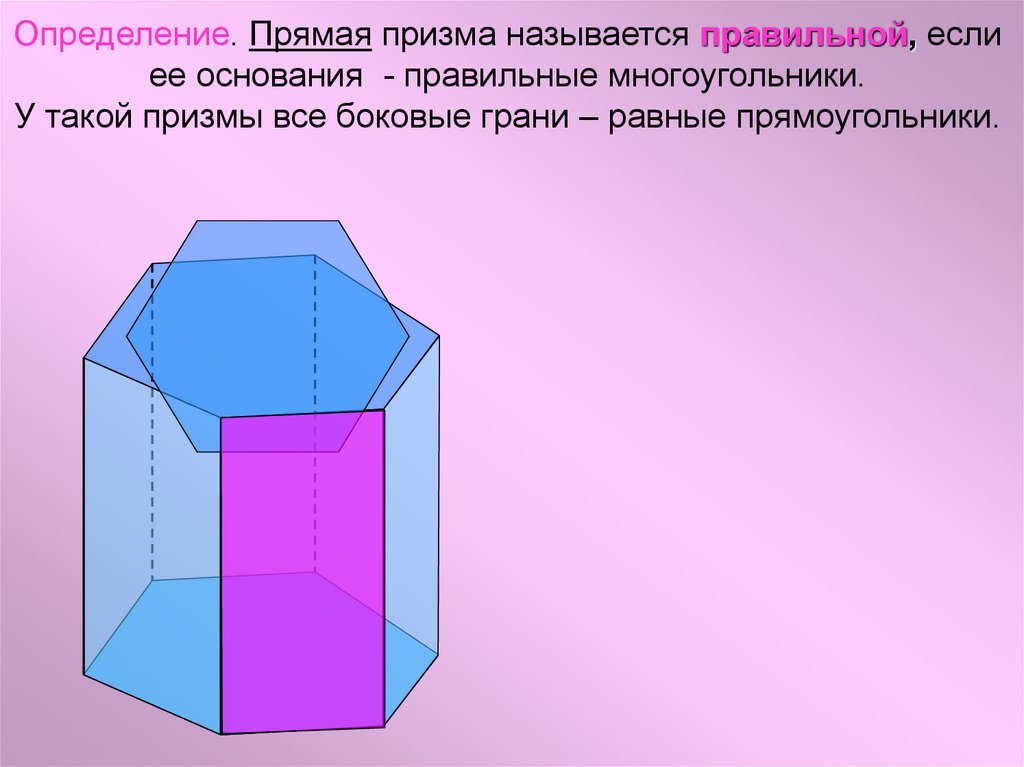
Определение. Прямая призма называется правильной, еслиее основания - правильные многоугольники.
У такой призмы все боковые грани – равные прямоугольники.
13.
Площадьповерхности
S бок Pсеч l
Прямая
призмы
S полн 2Sосн Sбок
призма
S бок Pосн H
Объем
V Sосн H
призмы
V Sсеч l





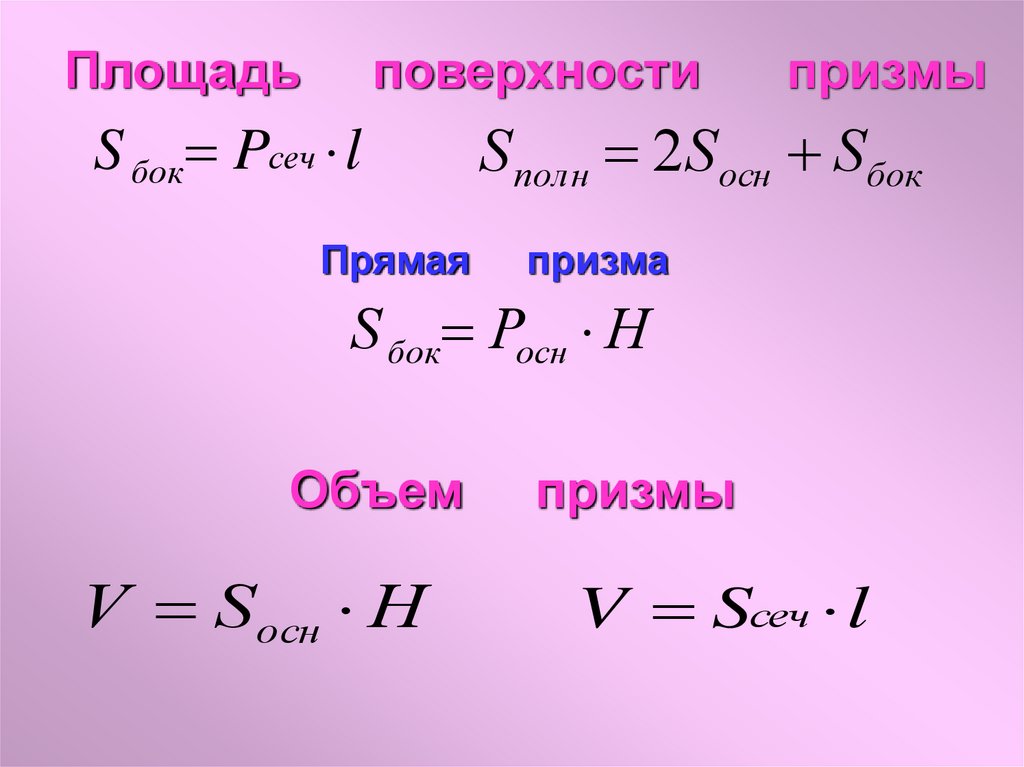
 mathematics
mathematics








