Similar presentations:
Почему у классического футбольного мяча шашечки двух типов: пятиугольные и шестиугольные
1.
Государственное бюджетное общеобразовательное учреждение школа№375 с углубленным изучением английского языка
Красносельского района Санкт-Петербурга
ИНДИВИДУАЛЬНЫЙ ИТОГОВЫЙ ПРОЕКТ
«ПОЧЕМУ У КЛАССИЧЕСКОГО ФУТБОЛЬНОГО МЯЧА ШАШЕЧКИ ДВУХ
ТИПОВ: ПЯТИУГОЛЬНЫЕ И ШЕСТИУГОЛЬНЫЕ»
Работу выполнил ученик 9 «Г»:
Борзенко Алексей Васильевич
Научный руководитель проекта:
Филиппова Нелли Михайловна
учитель алгебры и геометрии
Санкт-Петербург
2023 год
2.
ОглавлениеГлава 1. Введение ..................................................................................................................................2
Глава.2 Основная часть ..........................................................................................................................4
Глава 3. Заключение............................................................................................................................. 16
Литература ........................................................................................................................................... 17
Приложения ......................................................................................................................................... 18
1
3.
Глава 1. ВведениеПравильных многогранников вызывающе мало,
но этот весьма скромный по численности отряд
сумел пробраться в самые глубины различных наук.
Л.Кэрролл
Сегодня, наверно, нет человека в мире, который бы не знал что такое
футбол. Одни играют сами, другие предпочитают смотреть и болеть.
Первые официальные правила для игры в футбол были приняты в
Англии 8 декабря 1863 года. Именно с этой даты ведется отсчет
официальной игры в футбол. И этот день считается днем рождения футбола.
Без чего невозможно представит себе футбол? Правильно, без мяча!
Что может быть проще мяча?! А, между прочим, на создание этой
простой и совершенной конструкции люди потратили не одну сотню лет.
Зато сейчас любой человек, начиная с младенческого возраста, имеет
представление о мяче.
Чем же он замечателен?
Наблюдая за игрой любимой команды, большинство из нас даже не
задумываются об одном из самых важных элементов игры – футбольном
мяче. Казалось бы, чего о нем думать? Резиновый шар, накачанный воздухом
и обшитый прочной оболочкой – таким он представляется большинству
людей. На самом же деле, технология производства мяча и качество
материала интенсивно преобразуется на протяжении уже более 150 лет.
Какова же технология создания футбольного мяча? Какова его форма и
параметры?
В данном проекте постараюсь раскрыть, как взаимосвязаны математика
и футбольный мяч.
2
4.
Тип проекта – исследовательскийЦелью моей работы: выяснить как взаимосвязаны математика и форма
футбольного мяча.
Для достижения цели поставлены следующие задачи:
1. Изучить литературу по данному вопросу
2. Обобщить знания по математике и информатике
3. Привести доказательство влияния изготовления сферы мяча из
пяти/шестиугольников.
Объектом
работы
является
классический
футбольный
мяч
с
шашечками пяти/шестиугольников.
Предмет работы: пятиугольные и шестиугольные шашечки, из которых
состоит сфера мяча
Гипотезой данной работы является исследование усеченного икосаэдра
максимально приближенного к значению объема сферы, описанного около
икосаэдра.
Методы исследования:
знания, полученные за время учебы
знания из сети интернета и литературных источников
наблюдения.
Новизна проекта заключается в том, что продукт может понадобиться
на уроках информатики и геометрии.
3
5.
Глава.2 Основная частьРитуальные игры с мячом давно были распространены на всех
континентах.
В подобие игры, которую нынче называют футболом, люди играли еще
с древних времен. Пожалуй, самым основным элементов в этих играх был
мяч.
Существуют сведения, что первые мячи, которые более-менее
походили на современные, изготавливались из мочевых пузырей животных.
Однако подобный материал, как и сами мячи, быстро приходил в
непригодность, если по ним наносили достаточно сильные удары.
Его история начинается еще с Древнего Китая, где мячи шили из
кожаных мешков, набитых шерстью или перьями. Древнее римляне мячи
наполняли песком, потому они получались намного тяжелее их китайских
братьев. Мексиканские ацтеки использовали вместо мяча камень, который
оборачивали специальным прорезиненным материалом. Древние викинги
были завоевателями, а значит и футбол у них был особый, вместо мяча они
использовали головы своих пораженных врагов.
В Средневековье чаще всего в качестве мяча использовали емкости для
вина, которые делались из кожи. Форма и размеры этих мячей были разные, а
значит и отскок при ударе был непредсказуем, что делало игру динамичной и
быстрой. Основным правилом тех времен было, как можно дольше
продержать мяч в воздухе. Игра в мяч в это время была жестокой и он, в
основном, не доживал до конца, со временем пузырь начали обшивать
кусками кожи животных, это существенно удлинило ему жизнь.
Самый старый мяч, который сохранился до наших дней, находится в
шотландском замке Стирлинга, ему больше 450 лет. Он сделан из свиного
пузыря и обшит кусками кожи.
4
6.
Древние кожаные мячи были найдены при раскопках в Англии иГреции. Согласно преданиям античности, первый мяч дала Эросу богиня
Афродита, сказав ему такие слова: «Я дам тебе чудесную игрушку: это шар
быстро летучий, иной лучшей забавы ты не добудешь из рук Гефеста». В
зависимости от ритуала мяч мог символизировать и Солнце, и Луну, и
Землю, и даже полярное сияние. У индейцев это игра называлась Тапа Банка
Яп, у эскимосов тунгатгак, у китайцев цуцзю, а у итальянцев кальчо.
Настоящим прорывом в изготовлении мячей стал, запатентованый в
1836 году Чарльзом Гудиером вулканизированный каучук, на основании
которого в 1855 году был спроектирован совершенно новый футбольный
мяч, он сохранился до наших дней и красуется в национальном
Американском футбольном зале славы (Приложение 1).
Удачную альтернативу свиному пузырю в 1862 году изобрел Ричард
Линдон, заменив его резиновой камерой. Эта камера завоевала наивысшую
награду на выставке в Лондоне. С этого момента и началось серийное
производство мячей, бизнесом занялись такие компании как «Mitre» и
«Thomlinson’s of Glasgow». Они изготовляли мячи для Футбольной лиги
Англии. Цена зависела от качества кожи, которая использовалась для мяча. С
1872 года по 1937 год вес футбольного мяча составлял 368-425 г, сегодня вес
увеличили до 410-450 г.
Внешняя оболочка мяча состояла с 18 кожаных секций, которые
сшивались между собой конопляной веревкой с пяти слоев. Со временем
качество камеры улучшилось, и она стала выдерживать сильные удары, что
существенно повысило износостойкость мяча, а значит и качество футбола.
Такие мячи нам сегодня показались бы жутко неудобными, так как они
не были идеально круглыми, а натуральная кожа впитывала воду и заметно
тяжелела.
В послевоенное время мяч модернизировали плотной тканевой
прослойкой между камерой и внешним слоем, что позволило ему лучше
5
7.
держать форму, внешнюю кожу сменили на синтетику и непористыематериалы.
В 1951 году появились мячи белого и оранжевого цвета, которые были
лучше заметны при плохом осветлении и на снегу соответственно.
«Buckyball» — современный футбольный мяч (20 шестиугольников и
12 пятиугольников) изобрёл архитектор с Америки Ричард Бакминстер,
обдумывая как минимизировать количество материалов для строительства
зданий.
Мяч
В соответствии с новыми правилами, футбольный мяч должен иметь
сферическую форму с объёмом (длиной окружности) от 68,6 до 71,7 см.
Масса мяча могла колебаться в пределах от 368 до 425 граммов. В 1973 году
масса мяча была увеличена до 410—450 граммов, и с того момента это
правило останется неизменным и по сегодняшний день. Мяч состоял из
внутренней камеры и покрышки. Покрышка изготавливалась из натуральной
кожи и состояла из 18 сшитых между собой панелей (Приложение 2).
Ниппель был скрыт под шнуровкой.
В начале 1960-х был изготовлен
полностью синтетический футбольный мяч. Натуральная кожа всё ещё
находила применение в производстве, но в конце 1980-х синтетические
материалы полностью её заменили. Изначально покрышка изготовлялась из
натуральной кожи. Сейчас в основном применяют синтетику, поскольку
кожа впитывает воду и мяч набирает вес. Большинство современных мячей
состоят из 32 водонепроницаемых панелей. Панели футбольного мяча
сшивают нитками ручным или машинным способом или склеивают.
Сферическая форма придаётся мячу за счёт давления воздуха,
закачанного внутрь. Первый такой мяч был произведён в Дании в 1950 год
фирмой Select и получил в Европе широкое распространение. Всемирно стал
употребляться после чемпионата мира 1970 года, на котором были такие
мячи.
Платоновы тела
6
8.
Человек проявляет интерес к многогранникам на протяжении всейсвоей сознательной деятельности - от двухлетнего ребенка, играющего
деревянными кубиками, до зрелого математика. Некоторые из правильных и
полуправильных тел встречаются в природе в виде кристаллов, другие - в
виде вирусов, которые можно рассмотреть с помощью электронного
микроскопа.
Правильные многогранники с древних времен привлекали внимание
философов,
строителей,
архитекторов,
художников,
математиков.
Их
поражала красота, совершенство, гармония этих фигур.
Существует только пять правильных многогранников, а их гранями
могут быть только три типа правильных многоугольников: треугольники,
квадраты и пентагоны.
Эти правильные многогранники получили название Платоновых тел
(Приложение 3). Первое из них - это тетраэдр. Его гранями являются четыре
равносторонних треугольника. Тетраэдр имеет наименьшее число граней
среди Платоновых тел
и является
трехмерным
аналогом
плоского
правильного треугольника, который имеет наименьшее число сторон среди
правильных многоугольников. Следующее тело - это гексаэдр, называемый
также кубом. Гексаэдр имеет шесть граней, представляющие собой квадраты.
Гранями октаэдра являются правильные треугольники и их число в октаэдре
равно восьми. Следующим по количеству граней является додекаэдр. Его
гранями являются пентагоны и их число в додекаэдре равно двенадцать.
Замыкает пятерку Платоновых тел икосаэдр. Его гранями являются
правильные треугольники и их число равно 20.
В
древности
Платоновы
тела
ассоциировались
с
природными
стихиями. Тетраэдр олицетворял огонь, поскольку его вершина устремлена
вверх, как у разогревшегося пламени. Икосаэдр, как самый обтекаемый
символизирует воду. Куб - самая устойчивая фигура, символизирует землю.
Октаэдр – воздух.
7
9.
В наше время эту систему можно сравнить с четырьмя состояниямивещества: твердым, газообразным, жидким и пламенным
Пятый многогранник, додекаэдр, символизировал весь мир и почитался
главнейшим.
Архимедовы тела
Полуправильные многогранники — в общем случае это различные
выпуклые многогранники, которые, не являясь правильными, имеют
некоторые их признаки, например: все грани равны, или все грани являются
правильными
многоугольниками,
или
имеются
определённые
пространственные симметрии. Определение может варьироваться и включать
различные типы многогранников, но в первую очередь сюда относятся
архимедовы тела (Приложение 4).
Уделим особое внимание усеченному икосаэдру. Ведь именно этот
полуправильный многогранник определяет форму футбольного мяча.
Футбольный мяч – вовсе не шар.
Хотя считается, что футбольный мяч - это шар, на самом деле он
представляет собой многогранник, который, будучи заполненным воздухом,
принимает форму, близкую к сферической.
Футбольный мяч - это усеченный икосаэдр, гранями которого являются
20 правильных шестиугольников и 12 правильных пятиугольников. Это
архимедово тело имеет 32 грани, 90 ребер и 60 вершин.
Поверхность классического футбольного мяча состоит из «слегка
искривлённых» 12 правильных пятиугольников чёрного цвета и 20
правильных белых шестиугольников. Модель мяча можно представить себе
следующим образом. Из 12 правильных пятиугольников и 20 правильных
шестиугольников с равными сторонами можно сложить многогранник,
называемый усечённым икосаэдром.
Икосаэдр — один из пяти правильных многогранников. Его название
происходит от древнегреческих слов είκoσι— двадцать, έδρα — основание. У
8
10.
икосаэдра 12 вершин, 20 граней — правильных треугольников и 30 рёбер.(Приложение 5)
«Отрежем» (отсечём) вершины икосаэдра, отступив от вершин вдоль
прямых, направленных в центр, на столько, чтобы оставшиеся части граней
были
правильными
шестиугольниками.
Очевидно,
что
срезы
будут
правильными пятиугольниками. Получившаяся фигура и есть усечённый
икосаэдр.
Усечённый икосаэдр — один из полуправильных многогранников. Так
называются
многогранники,
у
которых
все
грани
—
правильные
многоугольники нескольких разных типов (в отличие от правильных
многогранников,
все
грани
которых
—
одинаковые
правильные
многоугольники), а все вершины устроены «одинаково», т. е. многогранные
углы при вершинах равны (совместимы).
Он занимает 86,74% объема описанной около него сферы, а будучи
заполненным воздухом - почти 95% ее объема. Хотя были изучены (и
изготовлены) мячи другой формы, сегодня усеченный икосаэдр по-прежнему
остается идеальной моделью футбольного мяча.
При «наполнении воздухом» усечённого икосаэдра он принимает
форму сферы, становится футбольным мячом. При этом вершины усечённого
икосаэдра совпадут с «вершинами мяча», рёбра перейдут в швы, а грани — в
«слегка искривлённые» многоугольники на поверхности мяча. Таким
образом, получится модель мяча — центральная проекция усечённого
икосаэдра на сферу.
9
11.
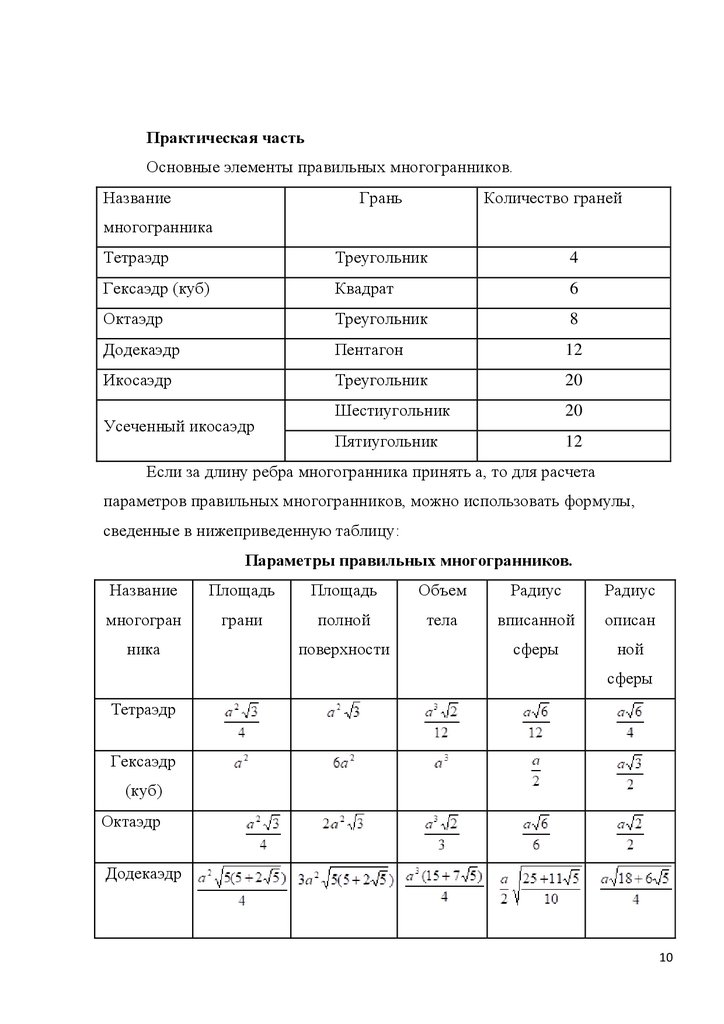
Практическая частьОсновные элементы правильных многогранников.
Название
Грань
Количество граней
многогранника
Тетраэдр
Треугольник
4
Гексаэдр (куб)
Квадрат
6
Октаэдр
Треугольник
8
Додекаэдр
Пентагон
12
Икосаэдр
Треугольник
20
Шестиугольник
20
Пятиугольник
12
Усеченный икосаэдр
Если за длину ребра многогранника принять a, то для расчета
параметров правильных многогранников, можно использовать формулы,
сведенные в нижеприведенную таблицу:
Параметры правильных многогранников.
Название
Площадь
Площадь
Объем
Радиус
Радиус
многогран
грани
полной
тела
вписанной
описан
сферы
ной
ника
поверхности
сферы
Тетраэдр
Гексаэдр
(куб)
Октаэдр
Додекаэдр
10
12.
ИкосаэдрНаибольшую проблему с вычислениями параметров представляет
усеченный икосаэдр. Усеченный икосаэдр – это полуправильный
многогранник, получаемый усечением вершин икосаэдра. В процессе
усечения грани икосаэдра превращаются в правильные шестиугольники, а на
месте удаленных вершин появляются правильные пятиугольники. Если
принять ребро икосаэдра, у которого будут усечены вершины за а, то
параметры усеченного икосаэдра приведены в таблице ниже:
Параметры усеченного икосаэдра
Параметр
Формула
Ребро икосаэдра
Ребро усеченного икосаэдра
Площадь пятиугольной грани
Площадь шестиугольной грани
Площадь полной поверхности
Радиус вписанной сферы
Радиус описанной сферы
Объем усеченного икосаэдра
Самая оптимальная форма, которую мог бы иметь футбольный мяч,
является сфера, или шарообразная оболочка. Но если накачивать резиновый
мяч воздухом для игры в футбол, то при ударе ногой он не будет
долговечным из-за своей непрочности. Для этого резиновую камеру мяча
обшивают кожаным кожухом, который имеет наибольшую прочность. Какой
же оптимальной формы должен быть мяч. То, что он имеет форму
11
13.
правильного или полуправильного многоугольника можно не сомневаться.Только такие многоугольники имеют несколько осей симметрии, что
позволяет мячу вращаться двигаться по заданной игроком траектории.
Проведем анализ, при какой же форме мяч будет иметь оптимальный
объем. Используя полученные данные, сравним объемы многогранников с
объемом описанной сферы, определяемой по формуле:
Процентная разница между объемами многогранника и описанной
около него сферы определяем по формуле:
Приводится сравнение полученных объемов многогранников с
объемом описанной вокруг многогранника сферы:
Для построения граней макета развертки усеченного икосаэдра
используется
алгоритм
построения
правильного
шестиугольника
12
14.
иалгоритм
построения
правильного
пятиугольника.
Попробуем данные расчеты применить на практике. С помощью
программного продукта AUTOCAD в котором ведется разработка,
проектирование и аннотирование 2D-геометрии и 3D-моделей с помощью
тел, поверхностей и объектов-сеток попробуем построить, многогранники и
сферу.
С помощью специальной команды «многоугольник» ведем значение 5
и построим пятиугольник. К одной из грани присоединим и также с
помощью специальной «многоугольник» ведем значение 6 и построим
шестиугольник.
Далее построим два эллипса по оси Х и по оси Z вместе где они
пересекаются, повернем шестиугольник гранью вместо пересечения.
13
15.
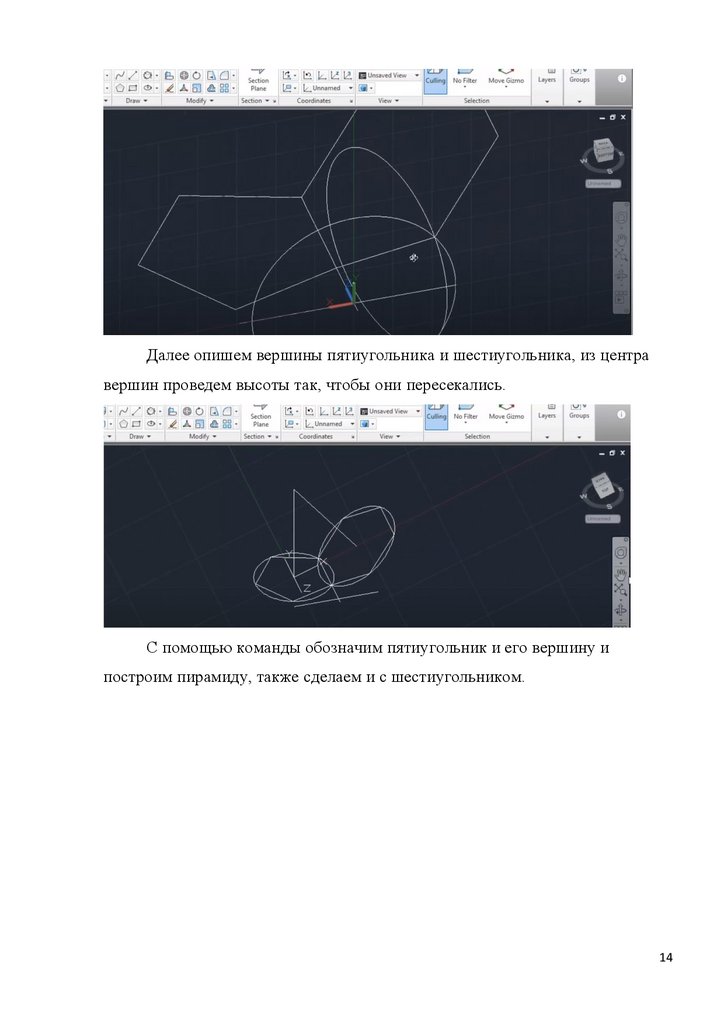
Далее опишем вершины пятиугольника и шестиугольника, из центравершин проведем высоты так, чтобы они пересекались.
С помощью команды обозначим пятиугольник и его вершину и
построим пирамиду, также сделаем и с шестиугольником.
14
16.
Из вершин опишем сферы в разных плоскостях, но таким образом,чтобы они не касались граней пятиугольников и шестиугольников.
Обрежем наши пирамиды относительно сферы и таким образом мы
получим полуправильные многогранники.
15
17.
Путем копирования полуправильных многогранников сшестиугольными гранями к пятиугольным граням, мы постепенно получим
сферу (то есть мяч).
Глава 3. Заключение
В результате выполнения работы были изучены Платоновы тела и тела
Архимеда. На основе свойств правильных многогранников (Платоновых тел),
были созданы материальная модель икосаэдра, усеченного икосаэдра
(футбольного мяча). Изучены и рассчитаны основные параметры правильных
многогранников и усеченного икосаэдра, зависящих от длины ребра:
площади граней и полной поверхности, объем многогранника, радиусы
описанной и вписанной сферы. Самая оптимальная форма, которую мог бы
иметь футбольный мяч, является сфера, или шарообразная оболочка. То, что
он имеет форму правильного или полуправильного многоугольника можно
не сомневаться. Только такие многоугольники имеют несколько осей
симметрии, что позволяет мячу вращаться двигаться по заданной игроком
16
18.
траектории. При проведении анализа было получено, что объем усеченногоикосаэдра максимально приближен к объему описанной около него сферы
(12%), что полностью подтверждает выдвинутую гипотезу.
С помощью правильных и полуправильных многогранников в
программном продукте AUTOCAD удалось построить модель футбольного
классического мяча.
Таким образом, изучение математики и практическое ее внедрение в
разные сферы жизни позволяет добиваться успехов в нашем современном
мире при помощи различных программных продуктов, позволяет узнавать
многое о простых вещах и помогает нашим инженерам, конструкторам в
самых разнообразных профессиях.
Литература
Энциклопедии
1. Математика: Школьная энциклопедия – 2003
Книги
2. Атанасян Л.С., Бутузов В.Ф. Геометрия 10-11 класс – 2008. - №14
3. Веленкин Н.Я. За страницами учебника математики: Арифметика.
Алгебра. Геометрия – 1996
4. Гончар В. В., Гончар Д. Р. Модели многогранников. Феникс, 2010. — 143
с
5. Депман И.Я. ,Веленкин Н.Я. За страницами учебника математики – 1989
6. Журин А.А. Учимся работать на компьютере. -М.: Лист, 2006
17
19.
7. Индейкин В. В. Табличный редактор Microsoft Excel. Учебное пособие. –Казань, 2005.
8. Математическая составляющая(М., 2015)
9. Паповский В.М. Углубленное изучение геометрии в 10-11 классах
10. Симанович С.В., Евсеев Г.А., Алексеев А.Г. Специальная информатика.
Учебное пособие.- М.:АСТ-ПРЕСС КНИГА; Инфорком-Пресс, 2006г.
Интернет- ресурсы
11. http://etudes.ru -сайт «Математические этюды»
12. https://www.nkj.ru/archive/articles/27921 Наука и жизнь, №1, 2016-01-21
Приложения
Приложение 1
Мяч Чарльза Гудиера
Приложение 2
18
20.
Сферическая форма усеченного икосаэдра при накачанной камерефутбольного мяча
Приложение 3
Приложение 4
19
21.
Приложение 5Икосаэдр
20




















 mathematics
mathematics sport
sport








