Similar presentations:
Сечение поверхности плоскостью. Тема 6
1. Тема 6
Пермский национальный исследовательскийполитехнический университет
Кафедра инженерной геометрии
Тема 6
Сечение поверхности плоскостью
Цель: сформировать навыки построения линии
пересечения поверхности плоскостью
2.
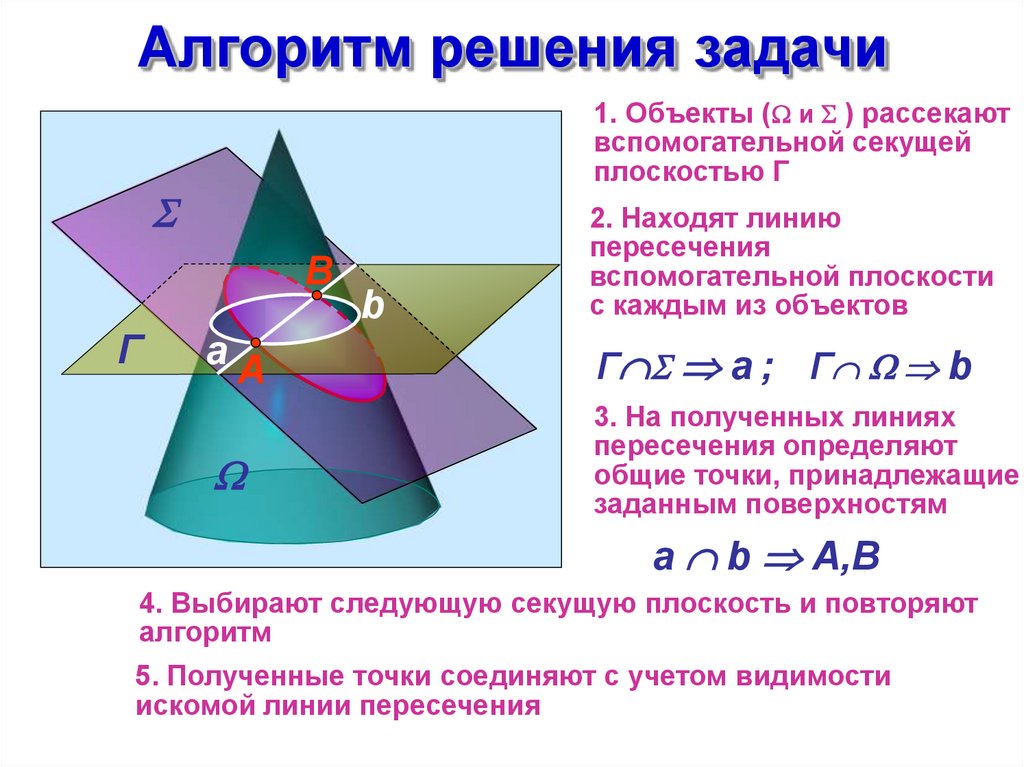
Алгоритм решения задачи1. Объекты ( и ) рассекают
вспомогательной секущей
плоскостью Г
B
Г
b
2. Находят линию
пересечения
вспомогательной плоскости
с каждым из объектов
аА
Г а ; Г b
3. На полученных линиях
пересечения определяют
общие точки, принадлежащие
заданным поверхностям
a b A,B
4. Выбирают следующую секущую плоскость и повторяют
алгоритм
5. Полученные точки соединяют с учетом видимости
искомой линии пересечения
3.
Методические указания• Вспомогательные плоскости следует
выбирать так, чтобы при построении
получались простые линии
• Сначала определяют опорные точки:
экстремальные точки, определяющие
границы искомой линии пересечения;
точки перемены видимости, лежащие на
очерке поверхности;
особые точки кривой сечения (вершины
эллипса, гиперболы или параболы,
вершины ломаной линии)
• Уточняют линию пересечения с помощью
промежуточных точек
4.
Методические указания• Плоскость, пересекающая поверхность, может
занимать общее и частное положение
относительно плоскостей проекций
• В общем случае вид сечения – кривая линия
• Сечение поверхности вращения плоскостью
является фигурой симметричной. Ось
симметрии фигуры сечения лежит в плоскости
общей симметрии заданных поверхности и
плоскости, удовлетворяющей условиям:
проходит через ось вращения поверхности;
перпендикулярна секущей плоскости
• Сечение многогранной поверхности есть
ломаная линия, вершины которой лежат на
ребрах поверхности
5.
Сечения прямого кругового цилиндра1
2
3
1
3
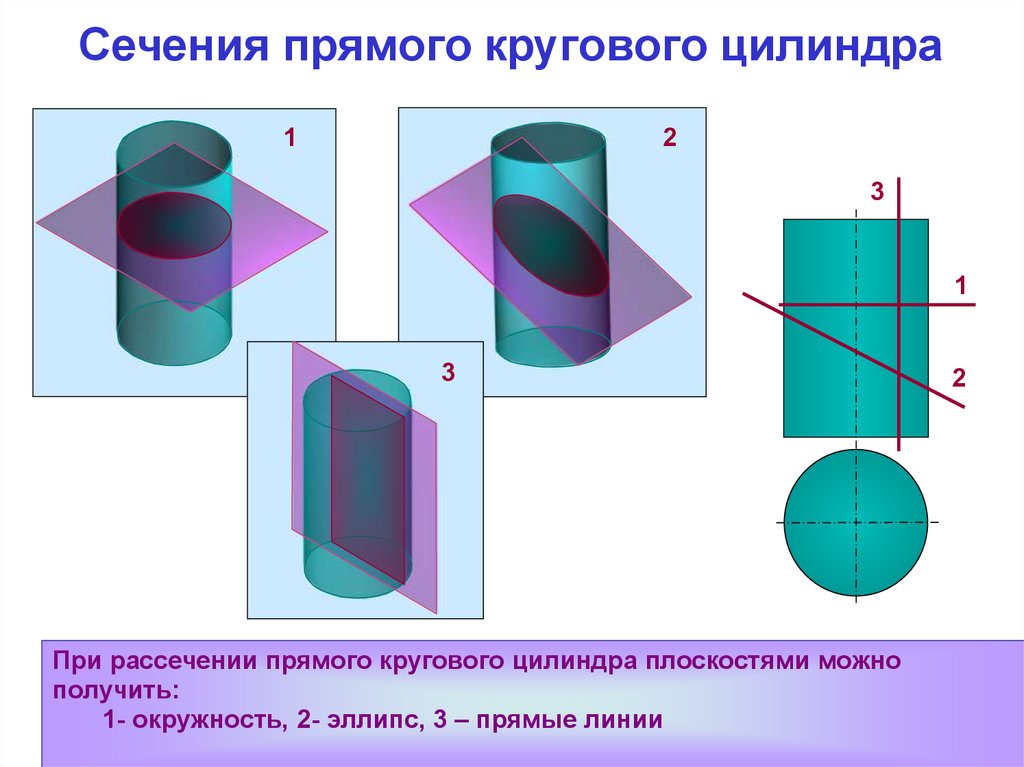
При рассечении прямого кругового цилиндра плоскостями можно
получить:
1- окружность, 2- эллипс, 3 – прямые линии
2
6.
Сечения прямого кругового конуса1
3
5
3
4
1
2
2
4
5
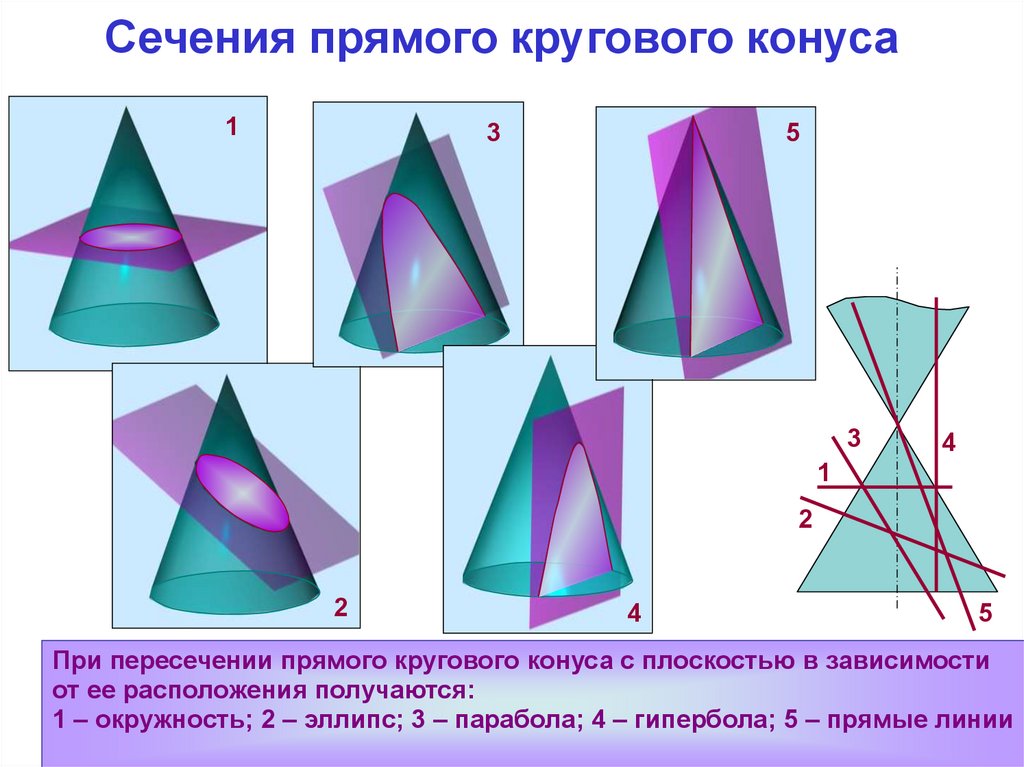
При пересечении прямого кругового конуса с плоскостью в зависимости
от ее расположения получаются:
1 – окружность; 2 – эллипс; 3 – парабола; 4 – гипербола; 5 – прямые линии
7.
2. ПО Сечение прямого кругового конусаΣ2
12
22 ≡ (32)
(13)
33
23
31
11
21
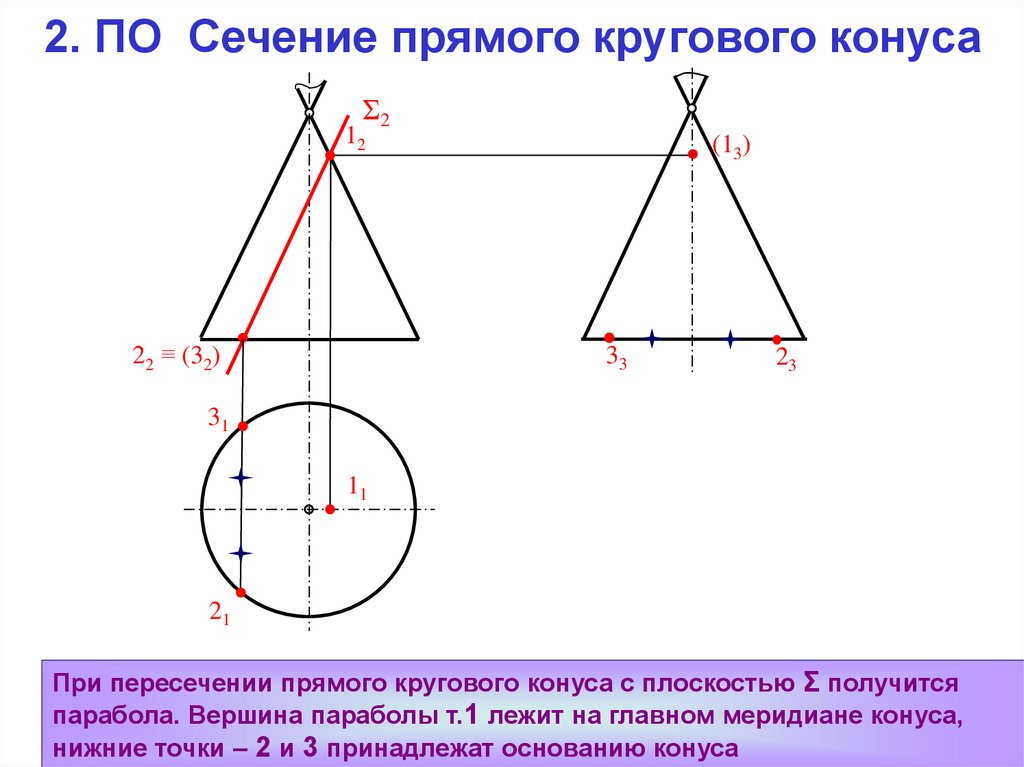
При пересечении прямого кругового конуса с плоскостью Σ получится
парабола. Вершина параболы т.1 лежит на главном меридиане конуса,
нижние точки – 2 и 3 принадлежат основанию конуса
8.
2. ПО Сечение прямого кругового конусаΣ2
12
42≡52
(13)
53
22 ≡ (32)
33
43
23
31
51
11
41
21
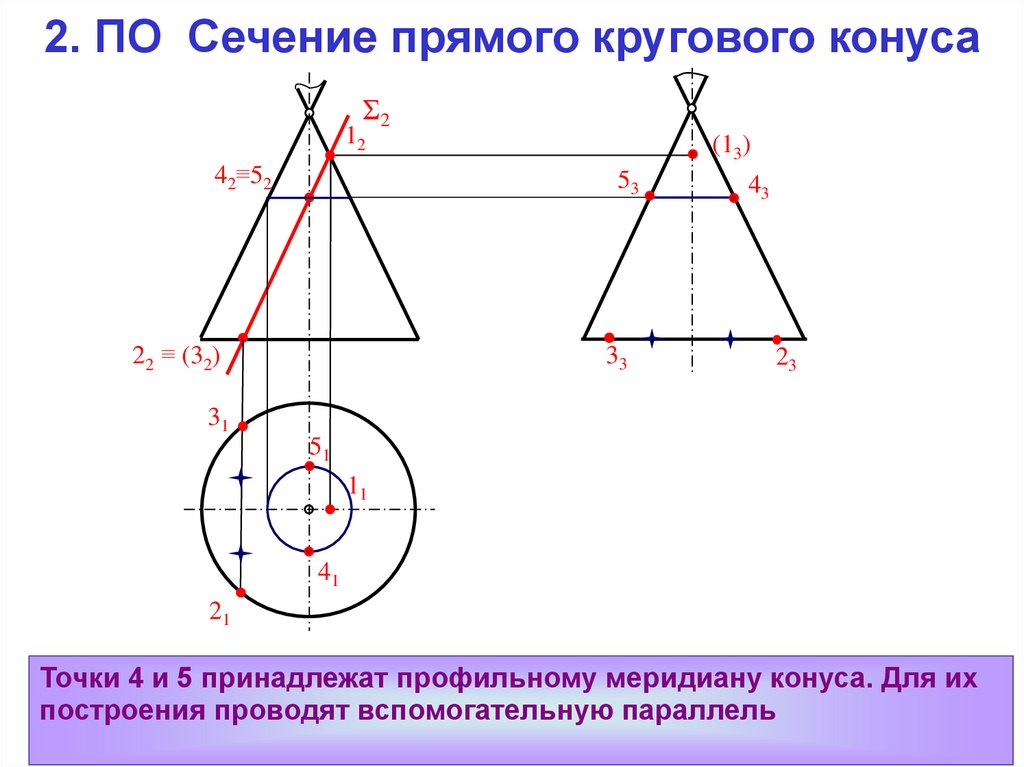
Точки 4 и 5 принадлежат профильному меридиану конуса. Для их
построения проводят вспомогательную параллель
9.
2. ПО Сечение прямого кругового конусаΣ2
12
42≡52
(13)
53
22 ≡ (32)
33
43
23
31
51
11
41
21
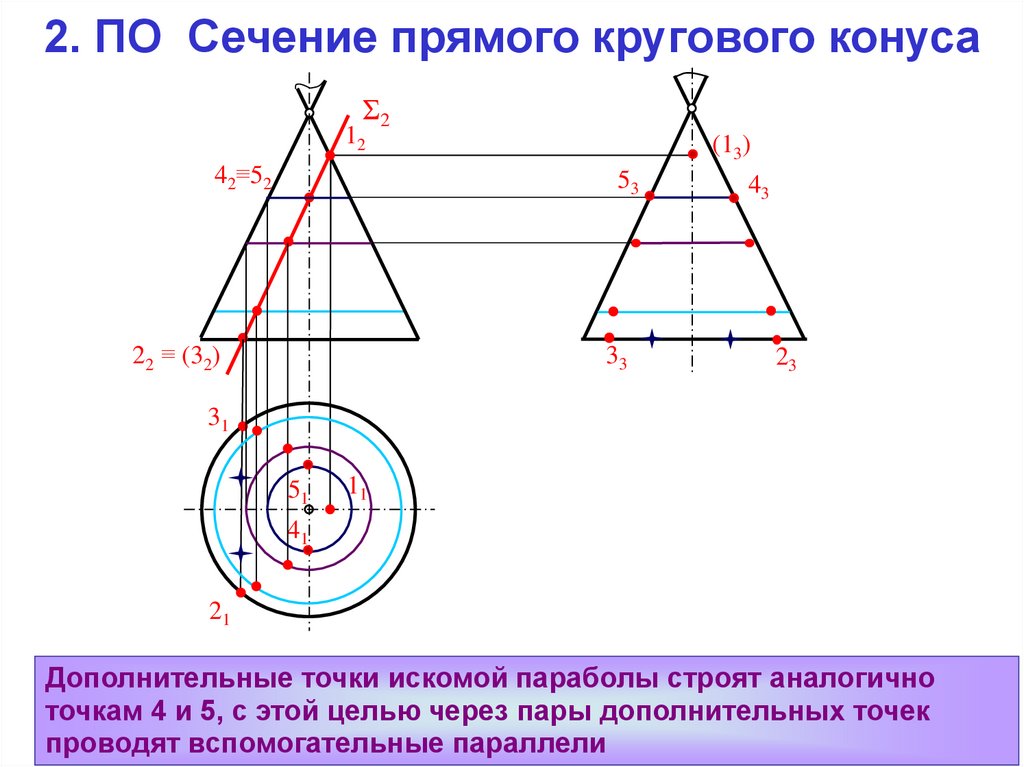
Дополнительные точки искомой параболы строят аналогично
точкам 4 и 5, с этой целью через пары дополнительных точек
проводят вспомогательные параллели
10.
2. ПО Сечение прямого кругового конусаΣ2
12
42≡52
(13)
53
22 ≡ (32)
33
43
23
31
51
11
41
21
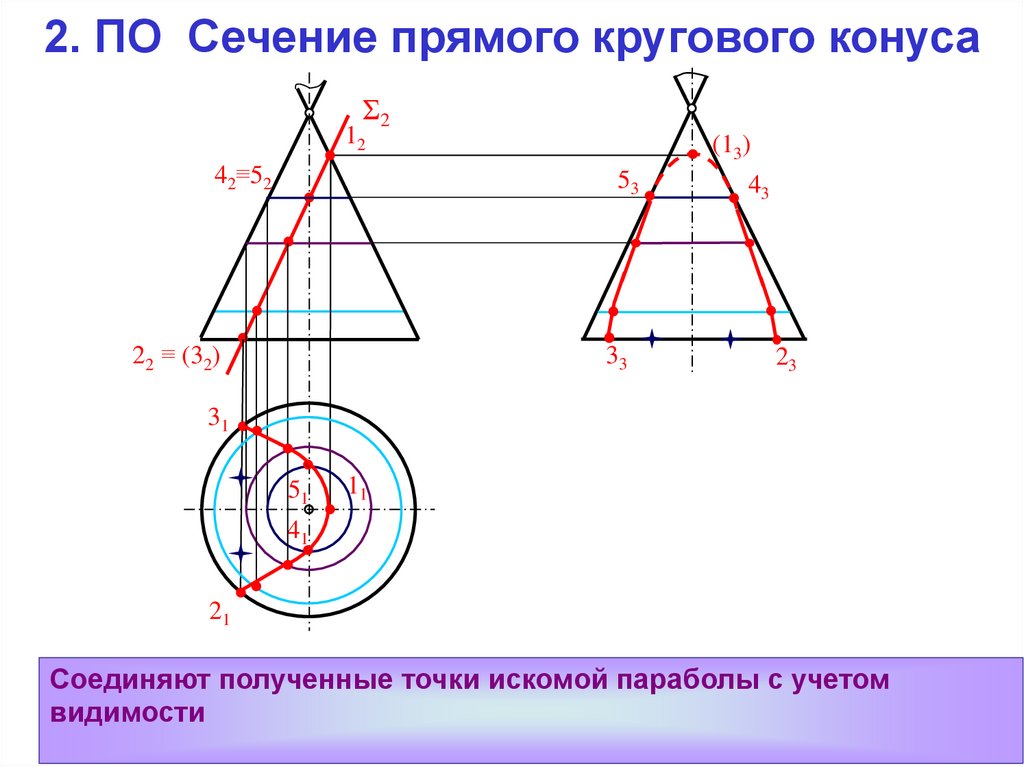
Соединяют полученные точки искомой параболы с учетом
видимости
11.
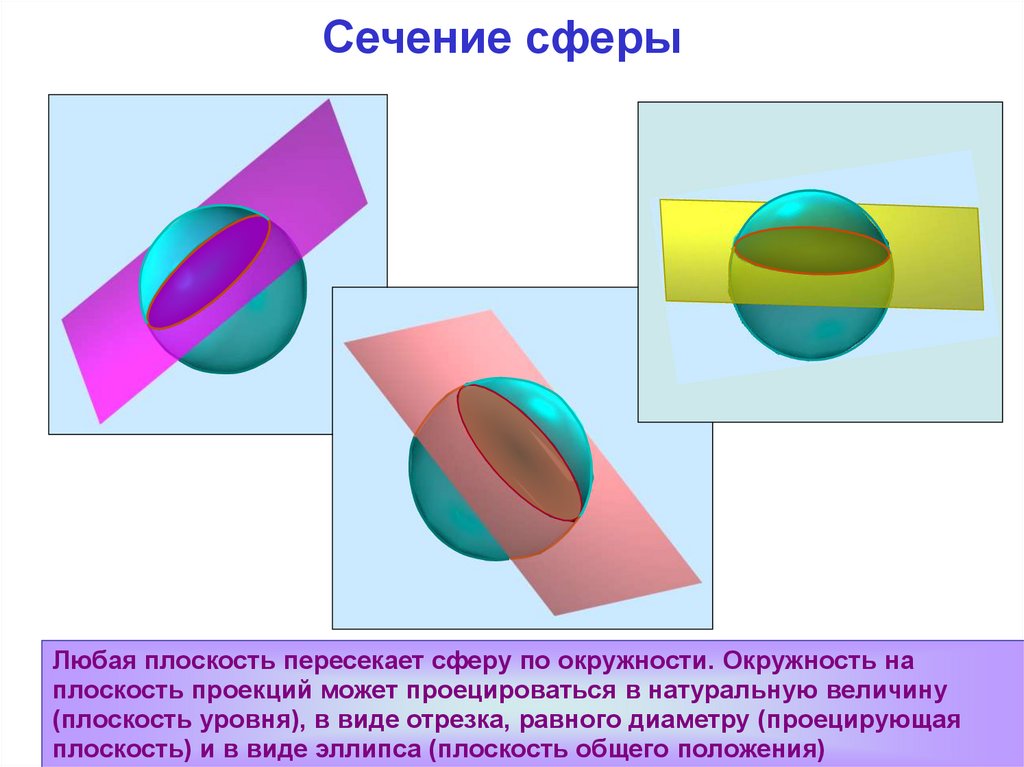
Сечение сферыЛюбая плоскость пересекает сферу по окружности. Окружность на
плоскость проекций может проецироваться в натуральную величину
(плоскость уровня), в виде отрезка, равного диаметру (проецирующая
плоскость) и в виде эллипса (плоскость общего положения)
12.
3.ПОQ2
22
О2
12
О1
21
Ф1
(11 )
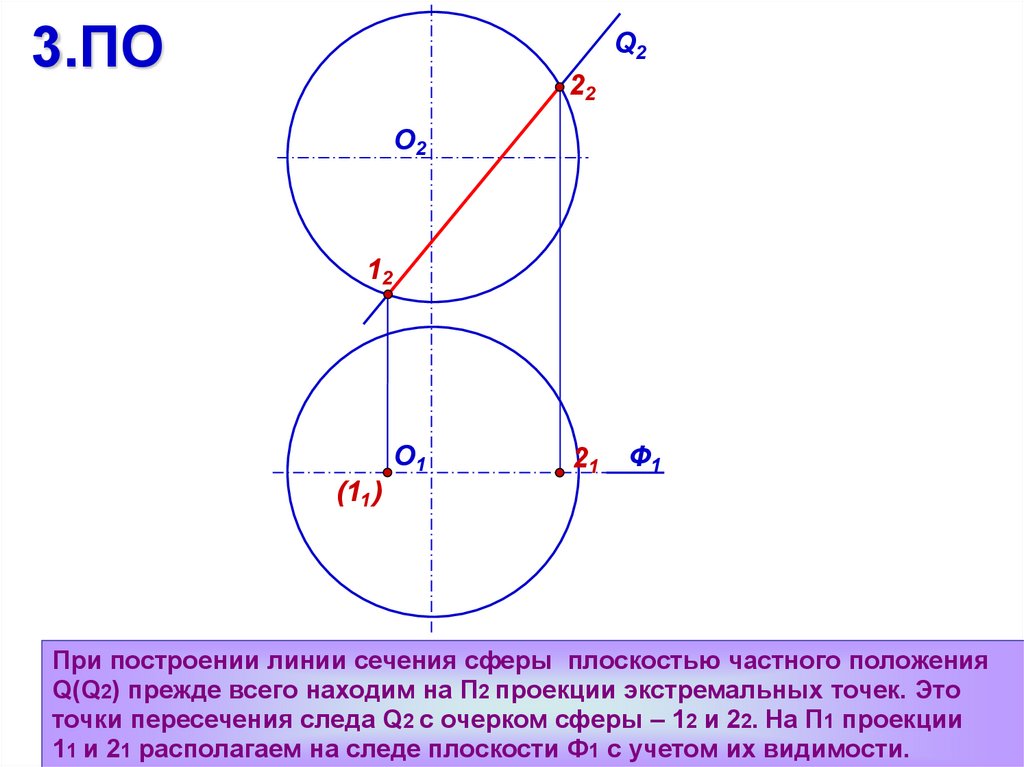
При построении линии сечения сферы плоскостью частного положения
Q(Q2) прежде всего находим на П2 проекции экстремальных точек. Это
точки пересечения следа Q2 с очерком сферы – 12 и 22. На П1 проекции
11 и 21 располагаем на следе плоскости Ф1 с учетом их видимости.
13.
3.ПОQ2
22
О2 32 (42)
Г2
12
41
О1
21
Ф1
(11 )
31
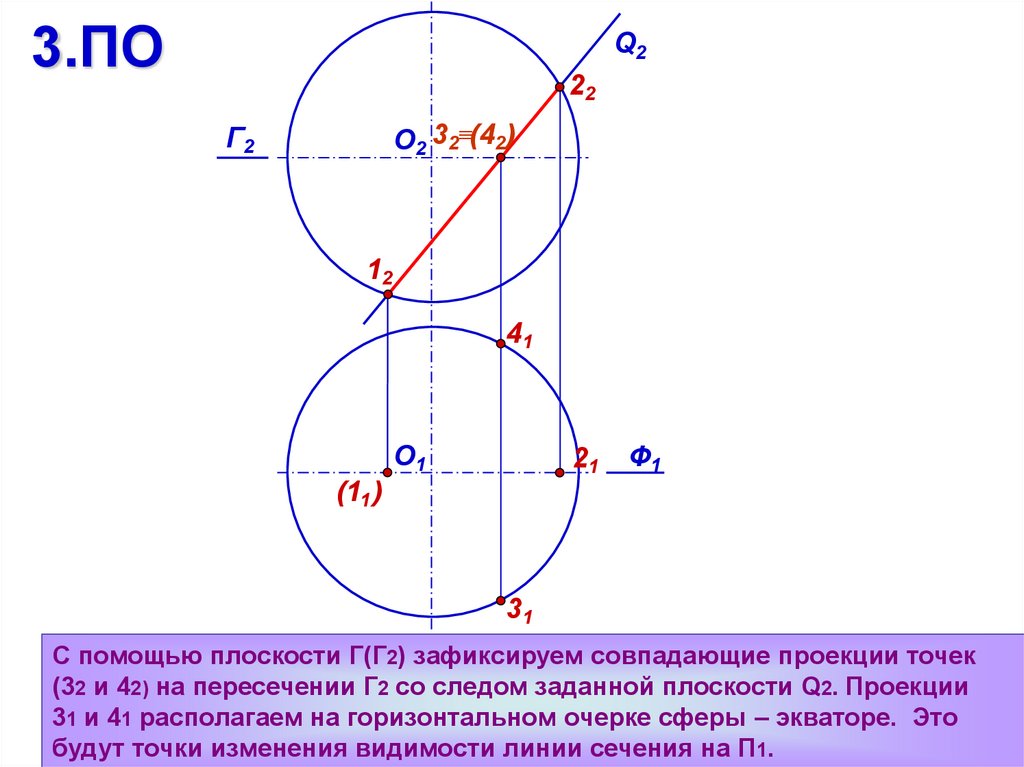
С помощью плоскости Г(Г2) зафиксируем совпадающие проекции точек
(32 и 42) на пересечении Г2 со следом заданной плоскости Q2. Проекции
31 и 41 располагаем на горизонтальном очерке сферы – экваторе. Это
будут точки изменения видимости линии сечения на П1.
14.
3.ПОQ2
22
О2 32 (42)
Г2
b2
52 (62)
12
(61 )
41
b1
О1
21
Ф1
(11 )
3
(51 ) 1
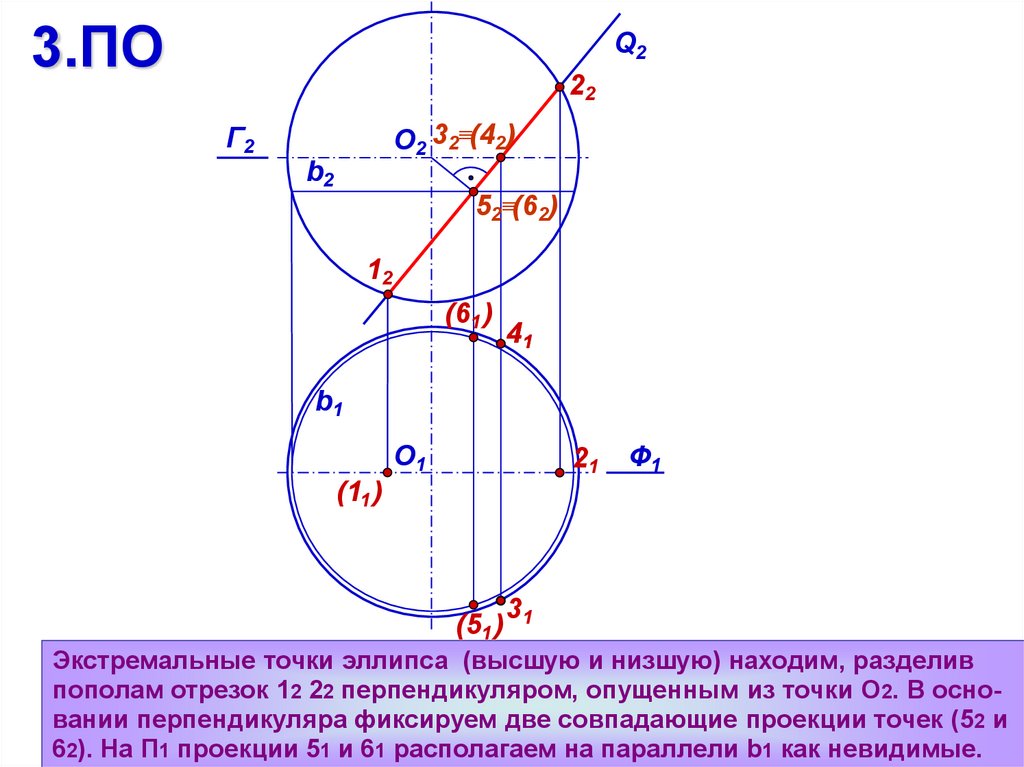
Экстремальные точки эллипса (высшую и низшую) находим, разделив
пополам отрезок 12 22 перпендикуляром, опущенным из точки О2. В основании перпендикуляра фиксируем две совпадающие проекции точек (52 и
62). На П1 проекции 51 и 61 располагаем на параллели b1 как невидимые.
15.
3.ПОQ2
22
О2 32 (42)
Г2
b2
52 (62)
с2
12
(61 )
41
b1
О1
21
Ф1
(11 )
с1
3
(51 ) 1
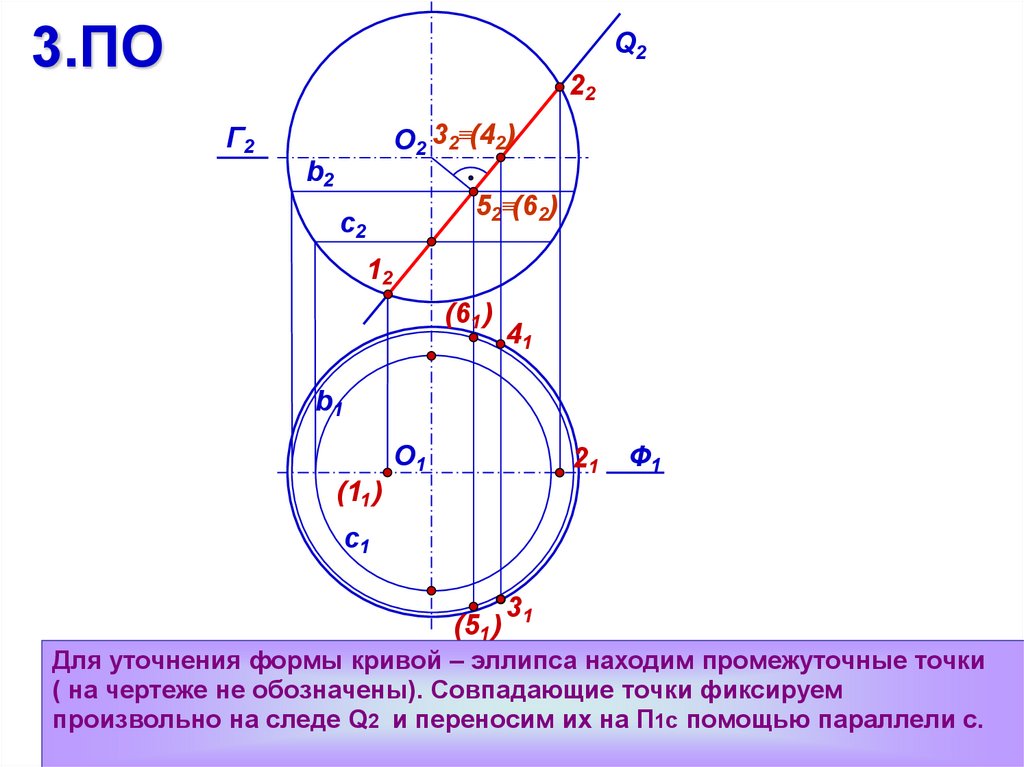
Для уточнения формы кривой – эллипса находим промежуточные точки
( на чертеже не обозначены). Совпадающие точки фиксируем
произвольно на следе Q2 и переносим их на П1с помощью параллели с.
16.
3.ПОQ2
22
О2 32 (42)
Г2
b2
52 (62)
с2
12
(61 )
41
b1
О1
21
Ф1
(11 )
с1
3
(51 ) 1
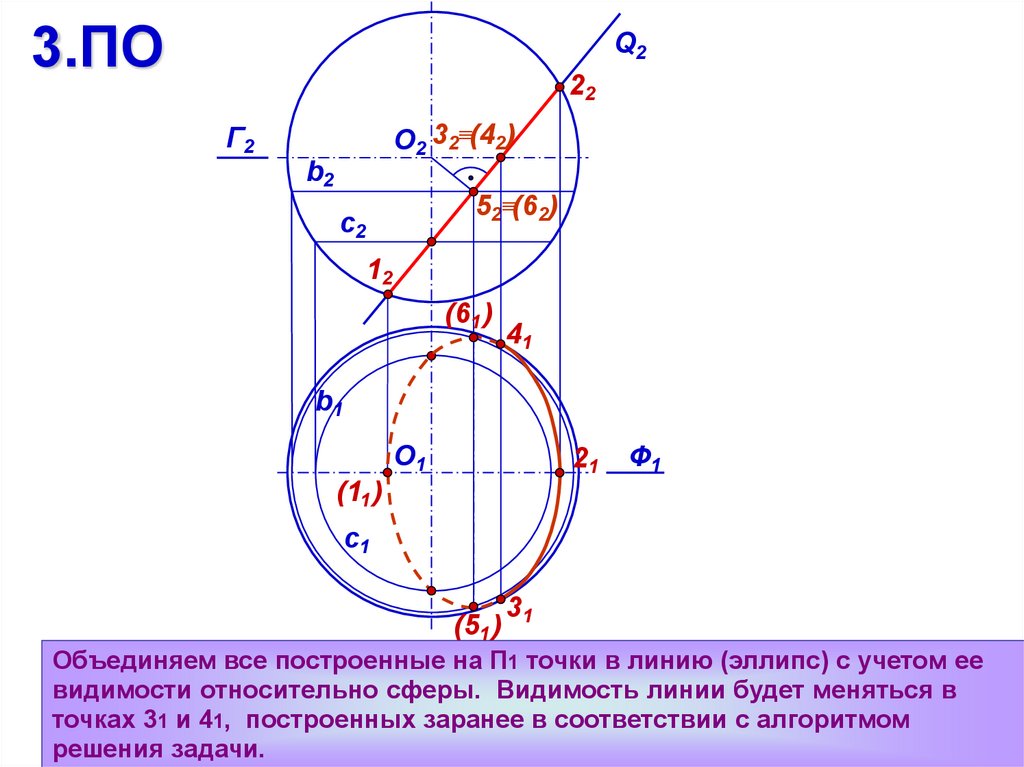
Объединяем все построенные на П1 точки в линию (эллипс) с учетом ее
видимости относительно сферы. Видимость линии будет меняться в
точках 31 и 41, построенных заранее в соответствии с алгоритмом
решения задачи.
17.
3.ПОQ2
22
О2 32 (42)
Г2
b2
52 (62)
с2
x
П2 x1
П4
12
П2
(61 )
П1
41
b1
О1
21
(11 )
Ф1
О4
с1
3
(51 ) 1
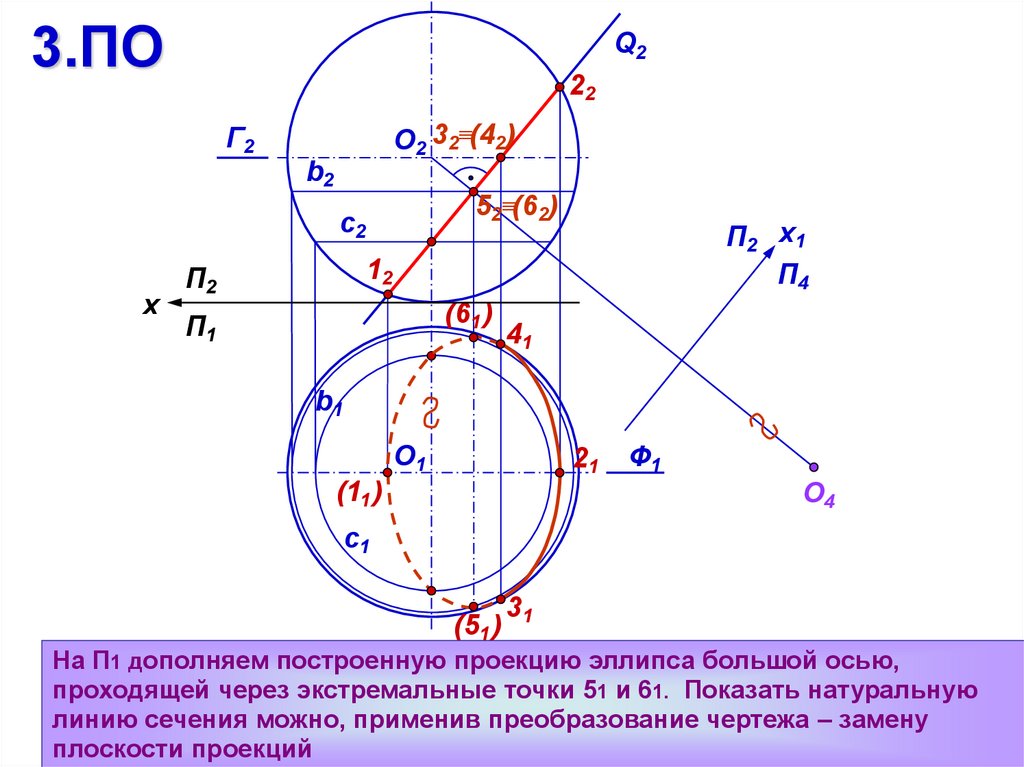
На П1 дополняем построенную проекцию эллипса большой осью,
проходящей через экстремальные точки 51 и 61. Показать натуральную
линию сечения можно, применив преобразование чертежа – замену
плоскости проекций
18.
3.ПОQ2
22
О2 32 (42)
Г2
b2
52 (62)
с2
x
12
П2
Rc
(61 )
П1
П2 x1
П4
41
b1
О1
21
(11 )
Rc
Ф1
О4
с1
3
(51 ) 1
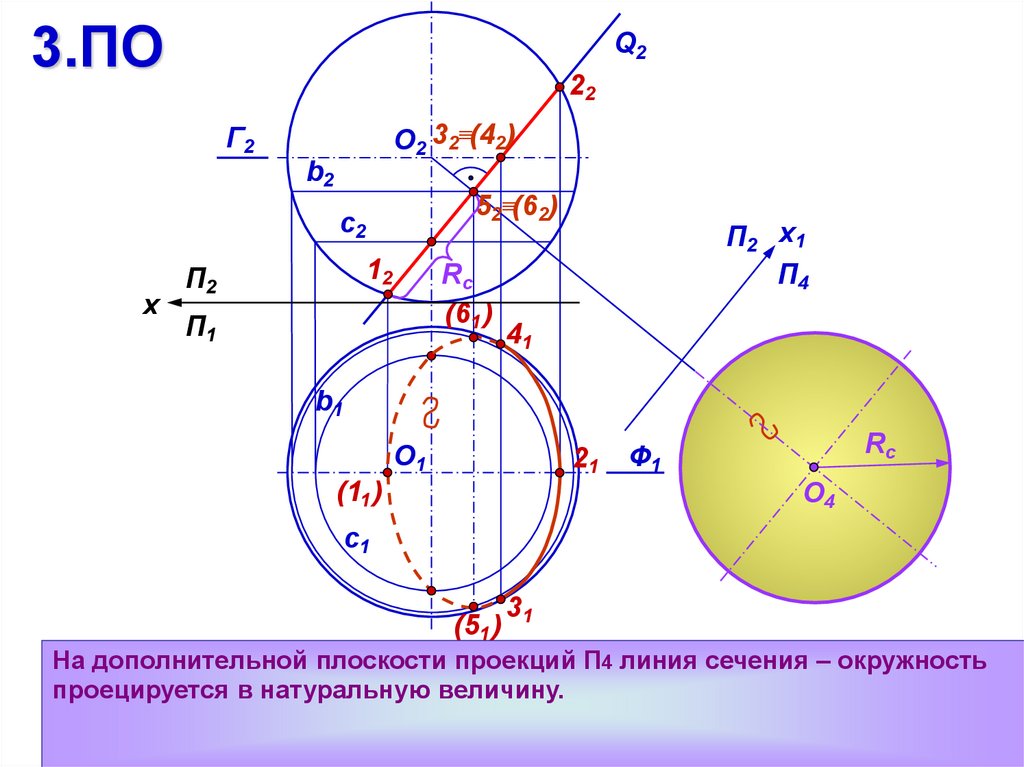
На дополнительной плоскости проекций П4 линия сечения – окружность
проецируется в натуральную величину.
19.
Нормальное сечение многогранникаa2
b2
c2
c1
a1
b1
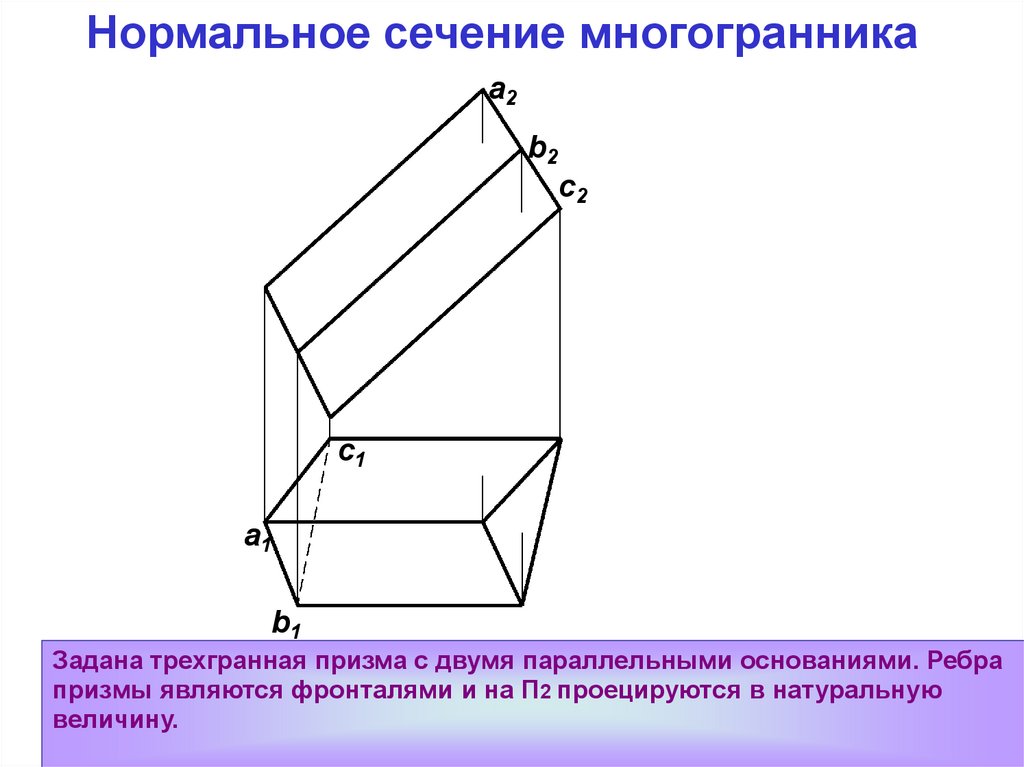
Задана трехгранная призма с двумя параллельными основаниями. Ребра
призмы являются фронталями и на П2 проецируются в натуральную
величину.
20.
Нормальное сечение многогранникаa2
b2
12
c2
22
32
P2
c1
a1
b1
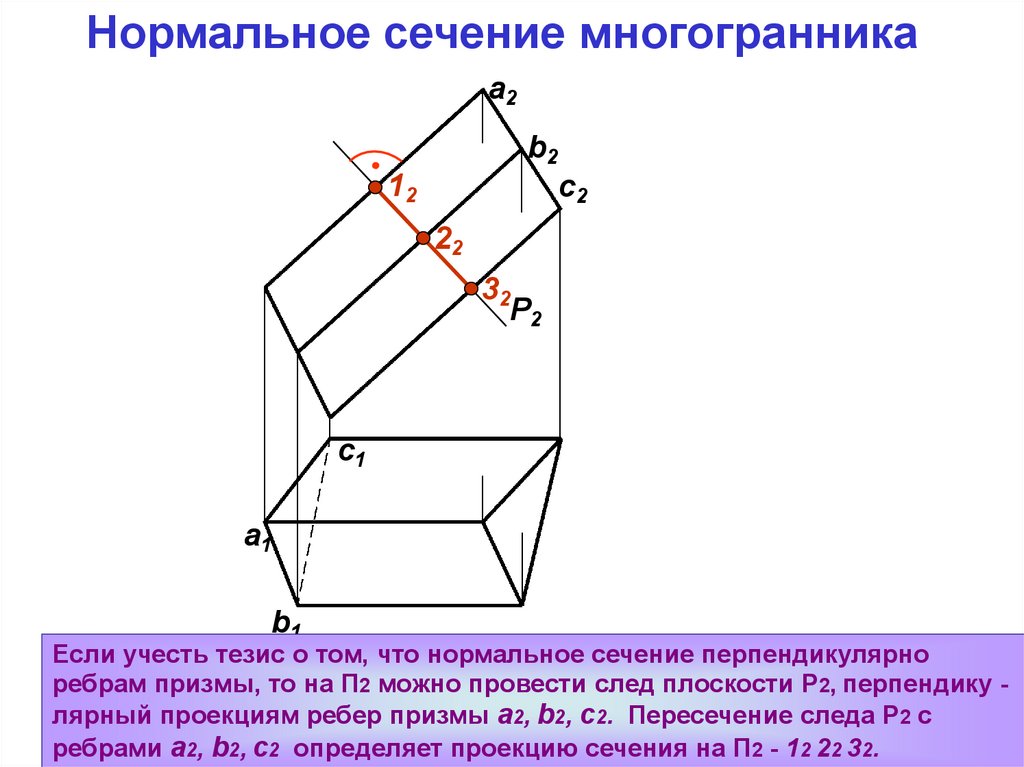
Если учесть тезис о том, что нормальное сечение перпендикулярно
ребрам призмы, то на П2 можно провести след плоскости Р2, перпендику лярный проекциям ребер призмы a2, b2, c2. Пересечение следа Р2 с
ребрами a2, b2, c2 определяет проекцию сечения на П2 - 12 22 32.
21.
Нормальное сечение многогранникаa2
b2
12
c2
22
32
P2
31
c1
11
a1
b1
21
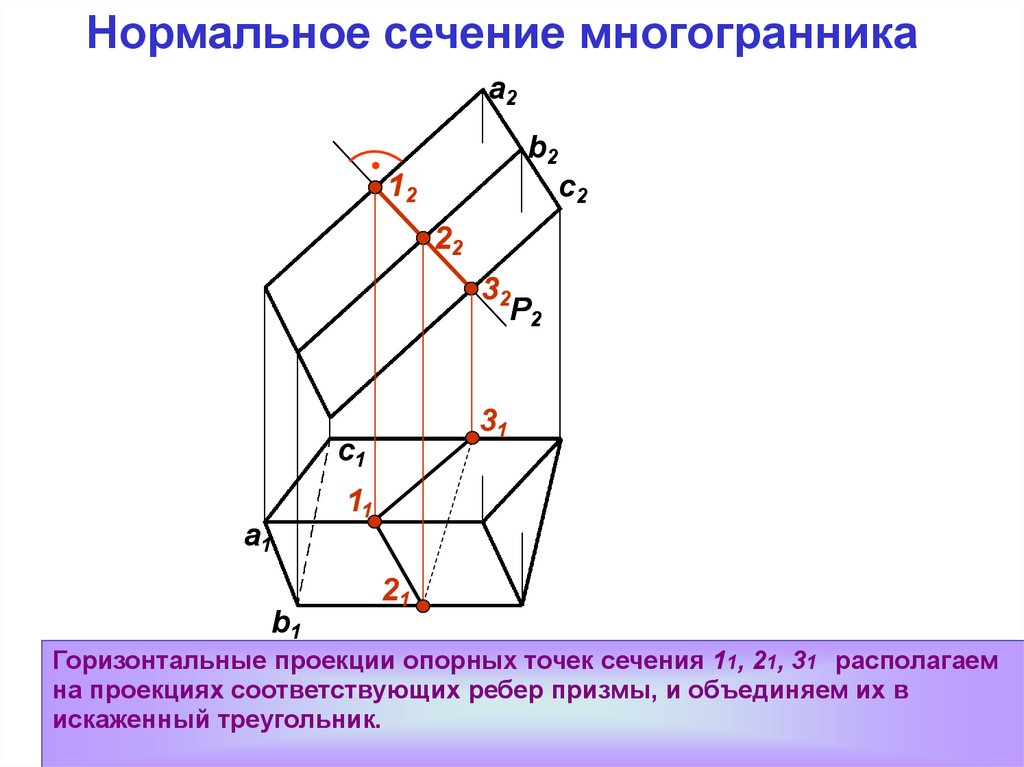
Горизонтальные проекции опорных точек сечения 11, 21, 31 располагаем
на проекциях соответствующих ребер призмы, и объединяем их в
искаженный треугольник.
22.
Нормальное сечение многогранникаa2
b2
12
c2
22
32
P2
12
22
32
31
c1
11
a1
b1
21
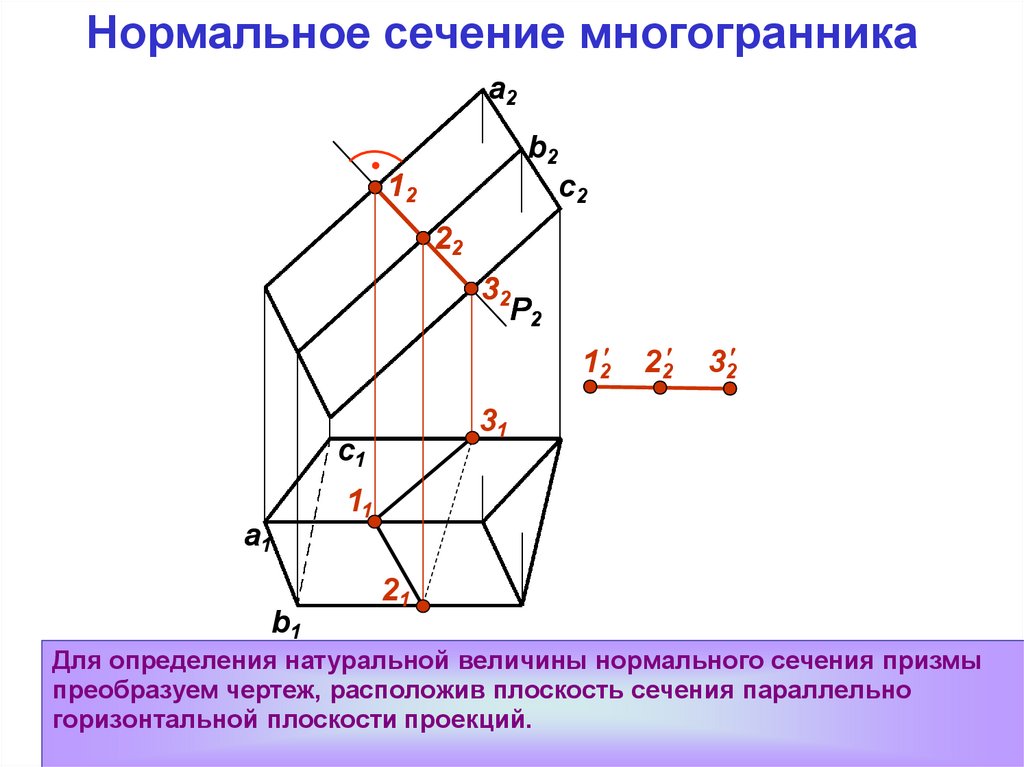
Для определения натуральной величины нормального сечения призмы
преобразуем чертеж, расположив плоскость сечения параллельно
горизонтальной плоскости проекций.
23.
Нормальное сечение многогранникаa2
b2
12
c2
22
32
P2
12
11
11
a1
b1
32
31
31
c1
22
21
21
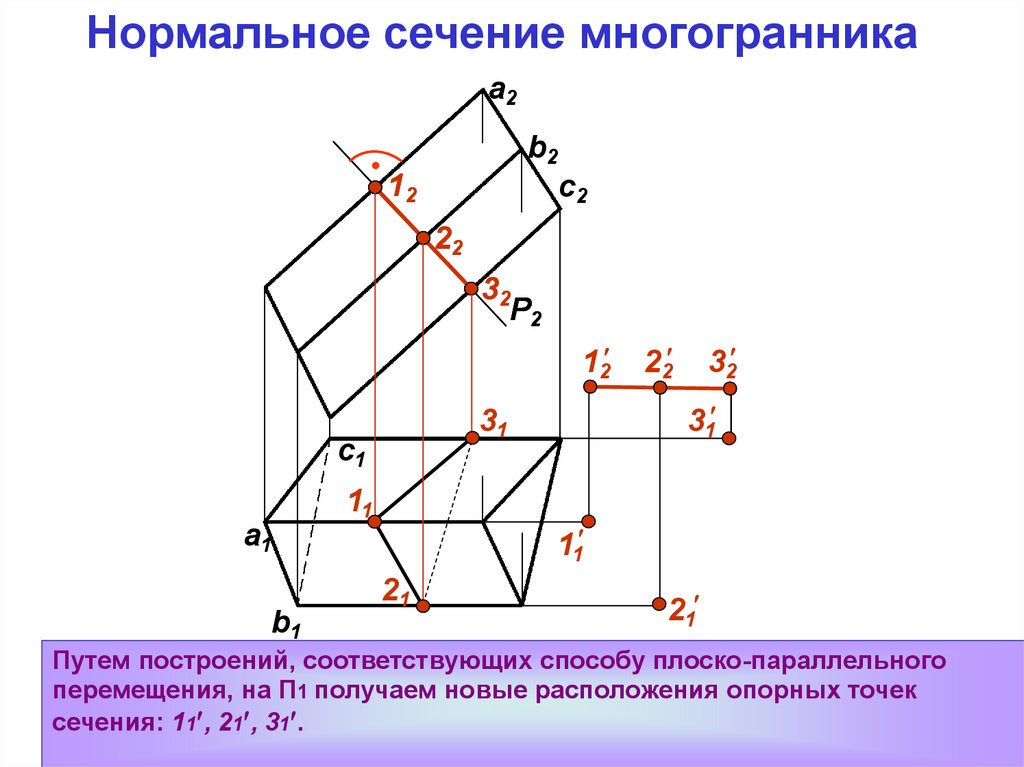
Путем построений, соответствующих способу плоско-параллельного
перемещения, на П1 получаем новые расположения опорных точек
сечения: 11 , 21 , 31 .
24.
Нормальное сечение многогранникаa2
b2
12
c2
22
32
P2
12
11
1
a1
1
21
32
31
31
c1
b1
22
н.
в.
21
Объединив на П1 новые проекции точек в треугольник, получим
натуральную величину нормального сечения призмы.




 mathematics
mathematics








