Графическая визуализация результатов вычислений

1.

1

2.

Основы двумерной графики
Построение графиков в ДСК
Функции одной переменной находят широкое применение в
практике математических и других расчетов, а также в технике
компьютерного
математического
моделирования.
Для
отображения функций вида у(х) используются графики в
декартовой (прямоугольной) системе координат. Поскольку
MATLAB – матричная система, совокупность точек у(х) задается
векторами X и Y одинакового размера.
Команда plot служит для построения графиков функций в
декартовой системе координат. Эта команда имеет различные
форматы вызова, рассматриваемые дальше.
2

3.

Команда PLOT
• plot(X,Y) – строит график функции у(х), координаты точек (х,у)
которой берутся из векторов одинакового размера Y и X.
- если x и y - вектора одинаковой длины и размерности (оба
строки или оба столбцы), то будет нарисована кривая y от x;
- если x - вектор, а y - матрица, строки или столбцы y будут
нарисованы в зависимости от x; если столбец матрицы y имеет ту же
длину, что и вектор x, то будет построен набор кривых,
представляющий зависимость каждого из столбцов от x; если строка
матрицы y имеет ту же длину, что и вектор x, то будет построен
набор кривых, представляющий зависимость каждой из строк от x; если
число строк и столбцов y одинаково, то строятся столбцы от x;
- если x -матрица, а y -вектор, то будет построено несколько
кривых, представляющих зависимость y от строк или столбцов
матрицы x по правилу, описанному в предыдущем пункте;
- если x и y -матрицы одинаковой размерности, то будет
построен набор кривых, представляющих столбцы y от столбцов x.
3

4.

Команда PLOT
Пример построения графика функций – у(х)=sin(x): на интервале от -4 до 4.
>>x = -4:.01:4;
>>y = sin(x);
>>plot(x,y);
>>
В результате выполнения
команд открывается
графическое окно
4

5.

Команда PLOT
Рассмотрим еще один пример построения графика y=e−x2 на интервале [-1.5
;1.5] .
>> x = - 1.5:.01:1.5;
>> y = exp(-x.ˆ2);
>> plot(x,y)
>>
В результате выполнения
команд открывается
графическое окно
5

6.

Команда PLOT
В системе MatLab можно также построить кривые, заданные параметрически.
>> t=0:.001:2*pi;
>> x=cos(3*t);
>> y=sin(2*t);
>> plot(x,y)
>>
В результате выполнения
команд открывается
графическое окно
6

7.

Команда PLOT
Аргументами функции
комбинации векторов и матриц:
plot()
могут
быть
различные
• plot(Y) – строит график функции у(k), где значения у берутся из
вектора Y, а k представляет собой индекс соответствующего
элемента. Если у содержит комплексные элементы, то выполняется
команда plot(real(Y), imag(Y)). Во всех других случаях мнимая часть
данных игнорируется.
В общем случае, число аргументов у команды plot() не
ограничивается двумя, то есть plot(x1,y1,x2,y2,...), причем правила,
описанные выше, относятся к каждой паре аргументов.
• plot(X1,Y1,S1,X2,Y2,S2,X3,Y3,S3,...) – эта команда позволяет
строить сразу несколько графиков различным цветом и стилем в
рамках одних и тех же осей координат.
7

8.

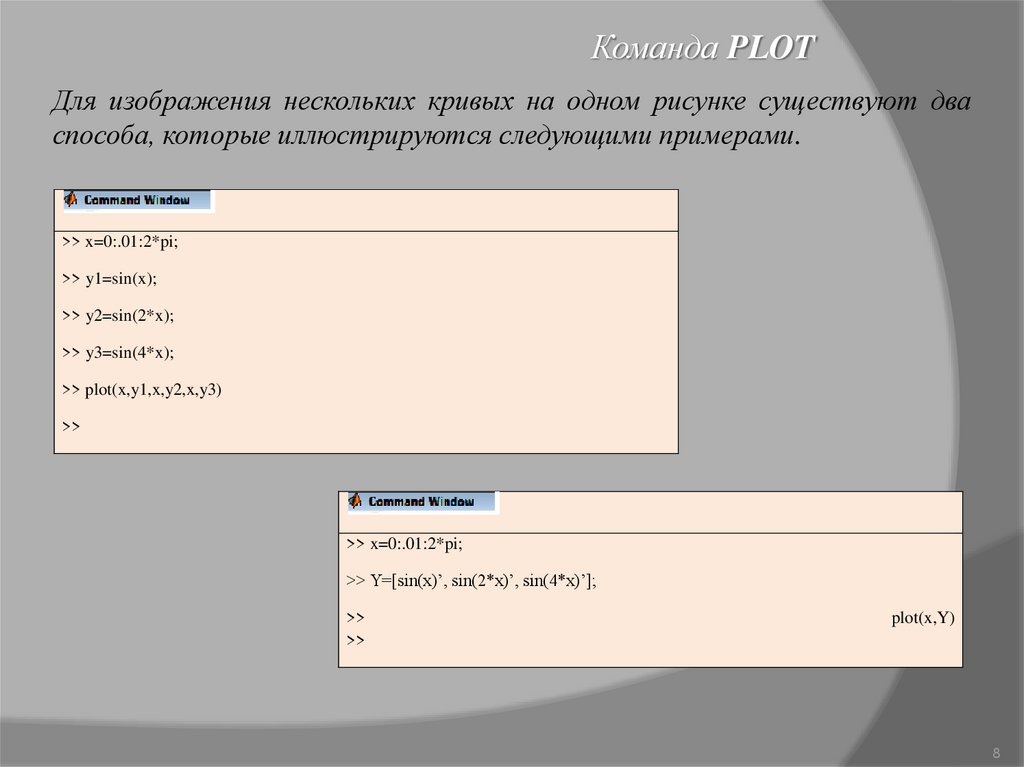
Команда PLOT
Для изображения нескольких кривых на одном рисунке существуют два
способа, которые иллюстрируются следующими примерами.
>> x=0:.01:2*pi;
>> y1=sin(x);
>> y2=sin(2*x);
>> y3=sin(4*x);
>> plot(x,y1,x,y2,x,y3)
>>
>> x=0:.01:2*pi;
>> Y=[sin(x)’, sin(2*x)’, sin(4*x)’];
>>
>>
plot(x,Y)
8

9.

Команда PLOT
Эти два примера полностью эквивалентны, а результат изображен на
рисунке. Отметим, что во втором примере формируется матрица Y,
содержащая значения изображаемых функций в виде столбцов.
Другим
способом
такого
отображения нескольких функции
на
одних
осях
является
использование команды hold on,
которая замораживает текущий
график, так что последующие
кривые размещаются на этом же
графике. При этом масштаб и
разметка осей изменяются, если
новая кривая не вписывается в
нарисованные оси. Команда hold
off приводит к тому, что любой
последующий вызов команды plot
создает новый рисунок в этом же
окне, то есть предыдущий график
стирается.
9

10.

Команда PLOT
При выводе графика можно сменить принятый по умолчанию тип
точек, с помощью которых рисуется данный график.
• plot(X,Y,S) – аналогична команде plot(X,Y), но тип линии графика можно
задавать с помощью строковой константы S. Значениями константы S
могут быть следующие символы. Таким образом, с помощью строковой
константы S можно изменять цвет линии, представлять узловые точки
различными отметками (точка, окружность, крест, треугольник с разной
ориентацией вершины и т. д.) и менять тип линии графика.
10

11.

Команда PLOT
Например, вызов команды plot(X,Y,'c*:') построит график функций
пунктирной линией голубого цвета со звездочками. При этом следует
отметить, что порядок символов в строковой константе не имеет
значение.
11

12.

Команда PLOT
>> x=0:.01:2*pi;
>> y1=sin(x);
>> y2=sin(2*x);
>> y3=sin(4*x);
>> plot(x,y1,’--’,x,y2,’:’,x,y3,’+’)
>>
12

13.

Основы двумерной графики
Построение графиков в ПСК
В полярной системе координат любая точка представляется как
конец радиус-вектора, исходящего из начала системы координат, имеющего
длину r и угол φ. Для построения графика функции r(φ) используются
приведенные ниже команды. Угол φ обычно меняется от 0 до 2*pi. Для
построения графиков функций в полярной системе координат используются
команды типа polar:
• polar(phi,r) – строит график в полярной системе координат,
представляющий собой положение конца радиус-вектора с длиной r и углом
phi;
• polar(phi,r,S) – аналогична предыдущей команде, но позволяет задавать
стиль построения с помощью строковой константы S по аналогии с
командой plot.
13

14.

Команда POLAR
>>
>>
>>
>>
phi=0:0.1:2*pi;
ro=5*(i+cos(phi));
polar(phi,ro);
title {'Кардиоида');
{'Кардиоида')
90
10
120
60
>> t=0:pi/50:2*pi;
>> polar(t,sin(5*t))
8
6
150
30
4
2
180
0
210
330
240
300
270
14

15.

Прочие возможности 2D-визуализации
Графики в логарифмическом и полулогарифмическом масштабе.
• loglog(...) – логарифмический масштаб используется для координатных
осей X и Y.
В некоторых случаях предпочтителен полулогарифмический
масштаб графиков, когда по одной оси задается логарифмический
масштаб, а по другой – линейный. Для построения графиков функций в
полулогарифмическом масштабе используются следующие команды:
• semilogx(...) – строит график функции в логарифмическом масштабе
(основание 10) по оси X и линейном по оси Y;
• semilogy(...) – строит график функции в логарифмическом масштабе по
оси Y и линейном по оси X.
Запись параметров (...) во всех трех функциях выполняется по аналогии с
функцией plot(...).
15

16.

Прочие возможности 2D-визуализации
Графики в логарифмическом и полулогарифмическом масштабе.
>>
x=0:10:100;
>> y=exp(x);
>> semilogy(x,y)
50
10
40
10
30
10
20
10
10
10
0
10
0
10
20
30
40
50
60
70
80
90
100
16

17.

Прочие возможности 2D-визуализации
Столбцовые диаграммы.
Для визуализации данных,
накопленных в массивах,
хорошо подходит специальная
графическая функция системы
MATLAB bar(...).
Гистограммы.
Для построения гистограммы
служит функция hist(...).
17

18.

Прочие возможности 2D-визуализации
Довольно интересной модификацией функции plot является функция fplot,
которая строит график функции y=f(x) без предварительного вычисления векторов
(x1,x2,…) и (y1,y2,...). Базовый формат вызова этой функции включает два аргумента:
fplot (@name_fun, [limits])
fplot (' name_fun', [limits])
Аргумент limits может быть представлен либо двухкомпонентным вектором
[xmin хmах], либо четырехкомпонентным вектором
[xmin xmax ymin ymax].
Укороченный вариант задает пределы изменения аргумента х, расширенный дополнительно представляет пределы изменения функции. Например:
fplot(@sin, [0 2*pi])
fplot('sin', [0 2*pi])
По сравнению с plot функция fplot берет на себя вычисление таблицы значения функции
- в местах резкого изменения функции значения аргумента х выбираются с более мелким
шагом. Функция fplot гарантирует, что относительное уклонение воспроизводимой
функции отличается от ее идеального графика не более чем на 0,2%. Если вам нужен
более точный или более грубый график, то после двух обязательных аргументов в
функции fplot можно задать желаемую относительную погрешность - число, меньшее
1:
fplot(@sin, [0 2*pi], 0.05)
18

19.

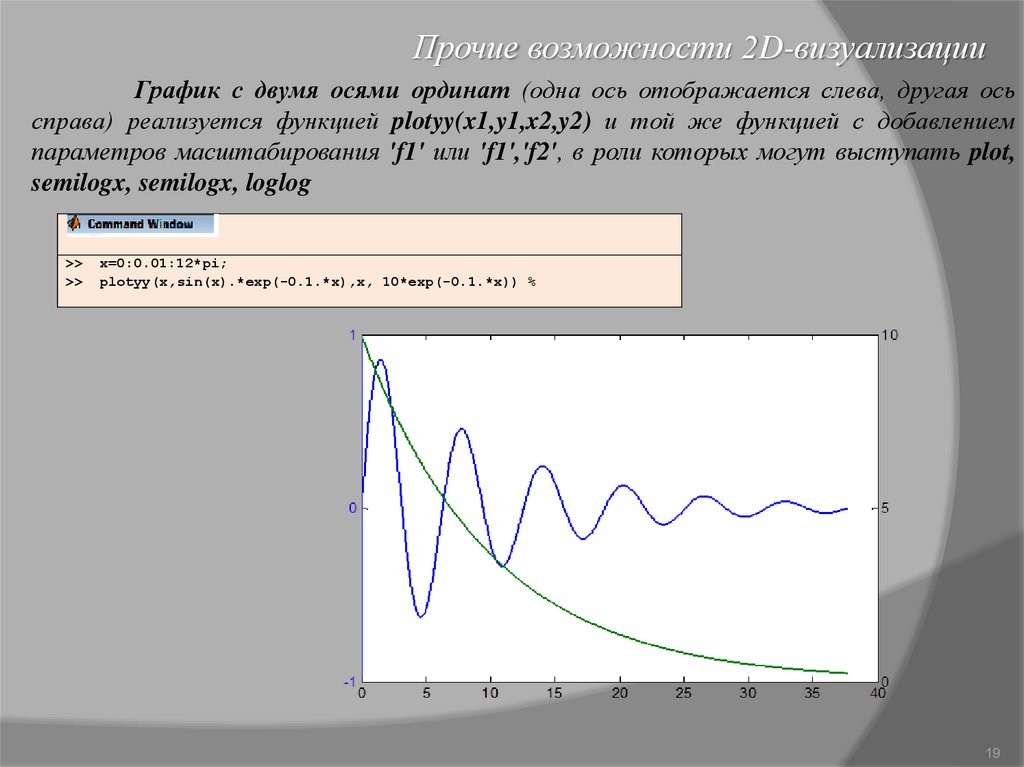
Прочие возможности 2D-визуализации
График с двумя осями ординат (одна ось отображается слева, другая ось
справа) реализуется функцией plotyy(x1,y1,x2,y2) и той же функцией с добавлением
параметров масштабирования 'f1' или 'f1','f2', в роли которых могут выступать plot,
semilogx, semilogx, loglog
>>
>>
x=0:0.01:12*pi;
plotyy(x,sin(x).*exp(-0.1.*x),x, 10*exp(-0.1.*x)) %
19

20.

Основы трехмерной графики
Создание массивов данных
Трехмерные поверхности обычно описываются функцией двух
переменных z(x,y). Специфика построения трехмерных графиков требует не
просто задания ряда значений х и у, то есть векторов х и y. Она требует
определения для X и Y двумерных массивов – матриц.
Для создания таких массивов служит функция meshgrid. В
основном она используется совместно с функциями построения графиков
трехмерных поверхностей. Функция meshgrid записывается в следующих
формах:
• [X,Y]=meshgrid(х,у) – преобразует область, заданную векторами x и y, в
массивы X и Y, которые могут быть использованы для вычисления функции
двух переменных и построения трехмерных графиков. Строки выходного
массива X являются копиями вектора x; а столбцы Y – копиями вектора y;
• [X,Y]=meshgrid(x) – аналогична [X,Y]=meshgrid(x,x);
>> [X,Y]=meshgrid(0:3,-3:0);
>> X =
0 1 2 3
0 1 2 3
0 1 2 3
0 1 2 3
>> Y =
-3 -3 -3 -3
-2 -2 -2 -2
-1 -1 -1 -1
0 0
0 0
20

21.

Графики поверхностей
Простейшей функцией в системе MATLAB для построения
трехмерных поверхностей – функция plot3(...), которая является аналогом
команды plot(...), но относится к функции двух переменных z{x,y). Она
строит аксонометрическое изображение трехмерных поверхностей и
представлена следующими формами:
• plot3(X,Y,Z), где X, Y и Z - три
матрицы одинакового размера,
строит точки с координатами
X(k,:), Y(k,:) и Z(k,:) и соединяет
их отрезками прямых.
>> [X,Y]=meshgrid([-3:0.15:3]);
>> Z=X.^2+Y.^2;
>> plot3(X,Y,Z)
• plot3(X,Y,Z,S) – обеспечивает построения, аналогичные рассмотренным
ранее, но со спецификацией стиля линий и точек, соответствующей
спецификации команды plot.
• plot3(X1,Y1,Z1,S1,X2,Y2,Z2,S2,X3,Y3,Z3,S3,...) – строит на одном рисунке
графики z1(x1,y1), z2(x2,y2) и т.д. со спецификацией линий и маркеров
каждой из них.
21

22.

Сетчатые 3D-графики с окраской
Наиболее представительными и наглядными являются сетчатые
графики поверхностей с заданной или функциональной окраской. В названии их
команд присутствует слово mesh. Имеется три группы таких команд.
• mesh(X,Y,Z) – выводит в графическое
окно сетчатую поверхность Z(X,Y).
При этом используется функциональная
окраска узлов, при которой цвет задается
высотой поверхности.
>> [X,Y]=meshgrid([-3:0.15:3]);
>> Z=X.^2+Y.^2;
>> mesh(X,Y,Z)
Иногда график поверхности полезно объединить с контурным графиком
ее проекции на плоскость, расположенным под поверхностью.
• meshc(...) – аналогична mesh(...), но
помимо графика поверхности дает
изображение ее проекции в виде
линий равного уровня
(графика типа contour).
22

23.

Сетчатые 3D-графики с окраской
Еще один тип представления поверхности, когда она строится из
многочисленных столбцов, дают команды класса meshz:
• meshz(...) – аналогична mesh(...), но строит поверхность как бы в виде
столбиков.
23

24.

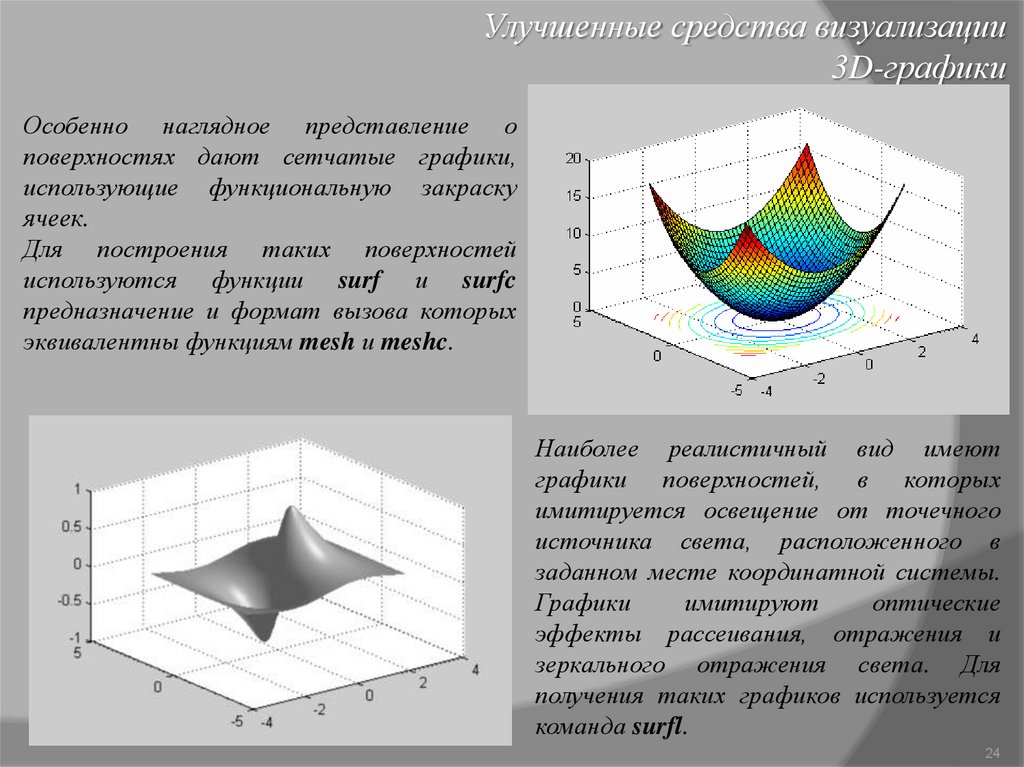
Улучшенные средства визуализации
3D-графики
Особенно наглядное представление о
поверхностях дают сетчатые графики,
использующие функциональную закраску
ячеек.
Для построения таких поверхностей
используются функции surf и surfc
предназначение и формат вызова которых
эквивалентны функциям mesh и meshc.
Наиболее реалистичный вид имеют
графики поверхностей, в которых
имитируется освещение от точечного
источника света, расположенного в
заданном месте координатной системы.
Графики
имитируют
оптические
эффекты рассеивания, отражения и
зеркального отражения света. Для
получения таких графиков используется
команда surfl.
24

25.

Контурные графики
В отличие от meshс (...) и surfс(...) функция contour рисует только линии
уровня соответствующих поверхностей и выступает в многообразии синтаксических
форм: contour(X,Y,Z) - для массива Z =Z(X,Y), contour(X,Y,Z,n) - то же с указанием
числа линий уровня (по умолчанию 10), contour(X,Y,Z,v) - то же для массива указанных
значений ;
Функция contourf(...) закрашивает области между линиями уровня,
аналогична contourf(...) с разницей в формате[C,h, cf]=contour (...), где cf определяет
матрицу раскраски.
>> [x,y]=meshgrid(-8:0.5:8);
>> t=sqrt(x.^2+y.^2)+0.001;
>> z=sin(t).^3./t;
>> [c,h]=contour(x,y,z,20);
>> [x,y]=meshgrid(-2:0.25:2);
>> t=sqrt(x.^2+y.^2)+0.001;
>> z=sin(t).^3./t;
>>[c,h,cf]=contourf(x,y,z,4);
25

26.

Контурные 3D-графики
Функция contour3(...) по синтаксису полностью
аналогична contour(...),
но изображает не
проекции линий уровня, а рисует
их в
пространственной интерпретации; так команда
[c,h]=contour3(x,y,z,20);
26

27.

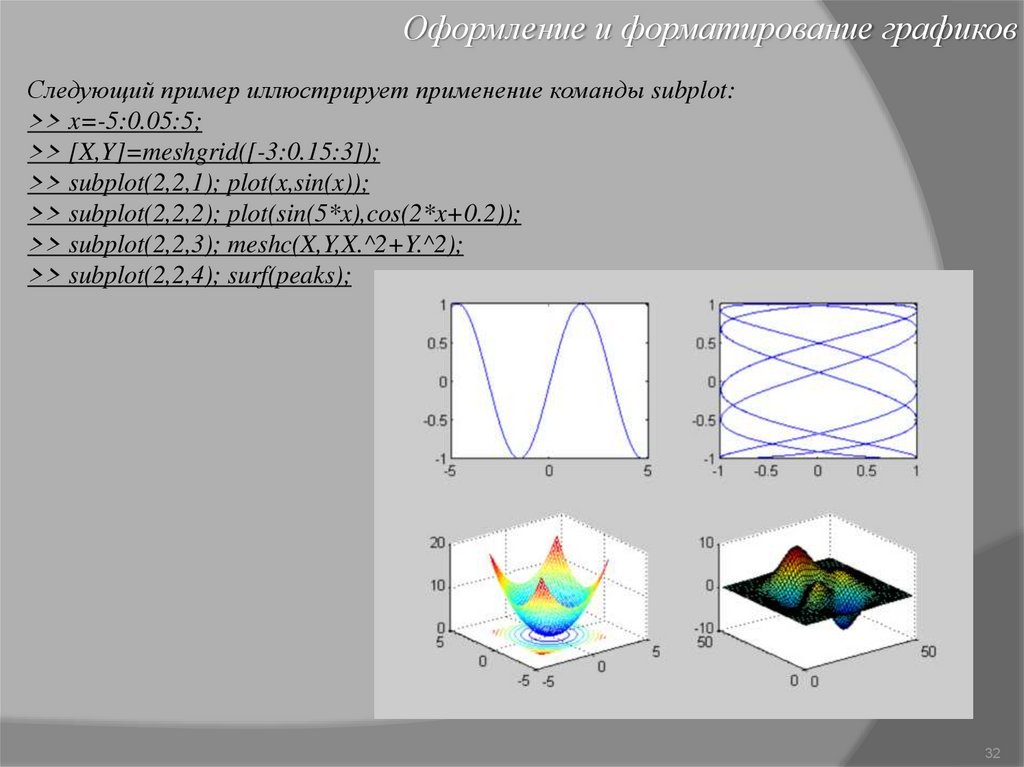
Оформление и форматирование графиков
Текстовое оформление графиков
После того как график уже построен, MATLAB позволяет выполнить его
форматирование или оформление в нужном виде. Соответствующие этому
средства описаны ниже.
• title('string') – установка на двумерных и трехмерных графиках титульной
надписи, заданной строковой константой 'string'.
• Для установки надписей возле осей х, у и z используются следующие команды:
xlabel('String')
ylabel('String')
zlabel('String')
Часто возникает необходимость добавления текста в определенное место
графика, например для обозначения той или иной кривой графика. Для этого
используется команда text:
• text(X,Y,'string') – добавляет в двумерный график текст, заданный строковой
константой 'string', так что начало текста расположено в точке с
координатами (X,Y).
• text(X,Y,Z,'string') – добавляет в трехмерный график текст, заданный
строковой константой 'string', так что начало текста расположено в позиции,
27
заданной координатами X, Y и Z.

28.

Оформление и форматирование графиков
>> x=1.5 : 0.1 : 2.5;
>> y=sin(x);
>> title (‘График sin(x)’);
>> xlabel(‘ось х’);
>> ylabel(‘sin(x)’);
>> text(2.1,0.9,f(x)=sin(x)’);
>>grid on
>>plot(x, y)
>>
График sin(x)
1
0.95
f(x)=sin(x)
0.9
sin(x)
0.85
0.8
0.75
0.7
0.65
0.6
0.55
1.5
1.6
1.7
1.8
1.9
2
2.1
2.2
2.3
2.4
2.5
ось х
28

29.

Оформление и форматирование графиков
Вывод пояснений и легенды.
Пояснение в виде отрезков линий со справочными надписями,
размещаемое внутри графика или около него, называется легендой. Для создания
легенды используются различные варианты команды legend. Некоторые из них:
• legend(stringl,string2,string3,...) – добавляет к текущему графику
легенду в виде строк, указанных в списке параметров;
• legend OFF – устраняет ранее выведенную легенду;
• legend – перерисовывает текущую легенду, если таковая имеется;
• legend(...,Pos) – помещает легенду в точно определенное место,
специфицированное параметром Pos: