Круги Эйлера

1.

2.

Задача № 1:
"Обитаемый остров" и "Стиляги“
Некоторые ребята из нашего класса
любят ходить в кино. Известно, что 15
ребят смотрели фильм «Обитаемый
остров», 11 человек – фильм «Стиляги»,
из них 6 смотрели и «Обитаемый
остров», и «Стиляги». Сколько человек
смотрели только фильм «Стиляги»?

3.

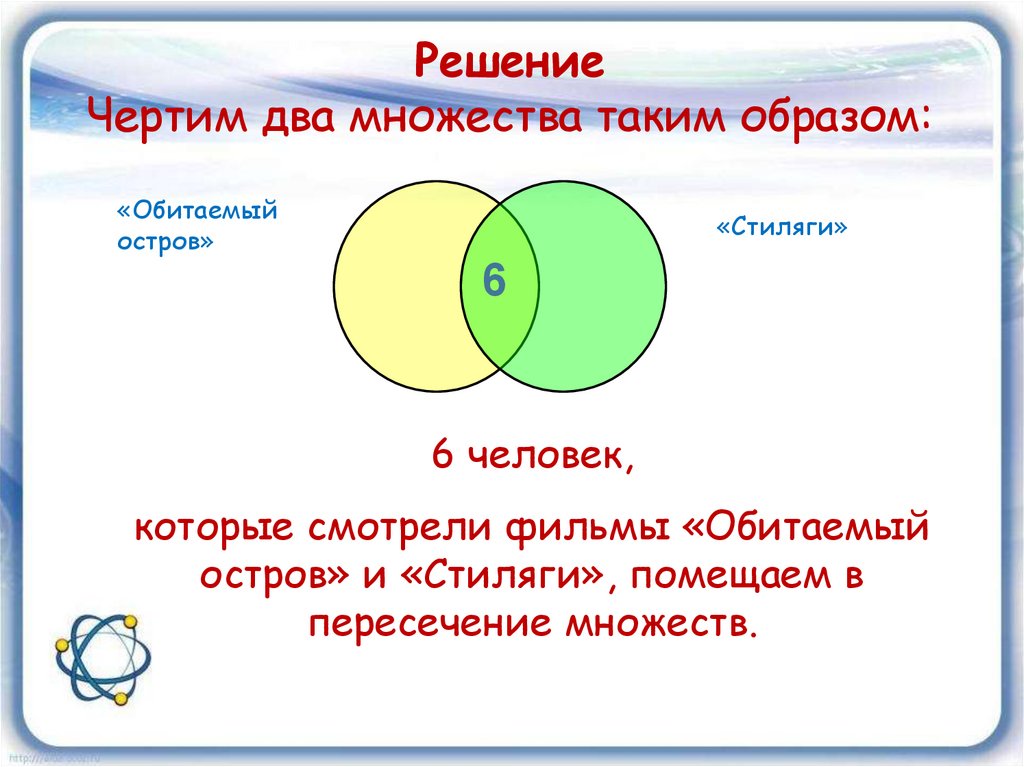
Решение
Чертим два множества таким образом:
«Обитаемый
остров»
«Стиляги»
6
6 человек,
которые смотрели фильмы «Обитаемый
остров» и «Стиляги», помещаем в
пересечение множеств.

4.

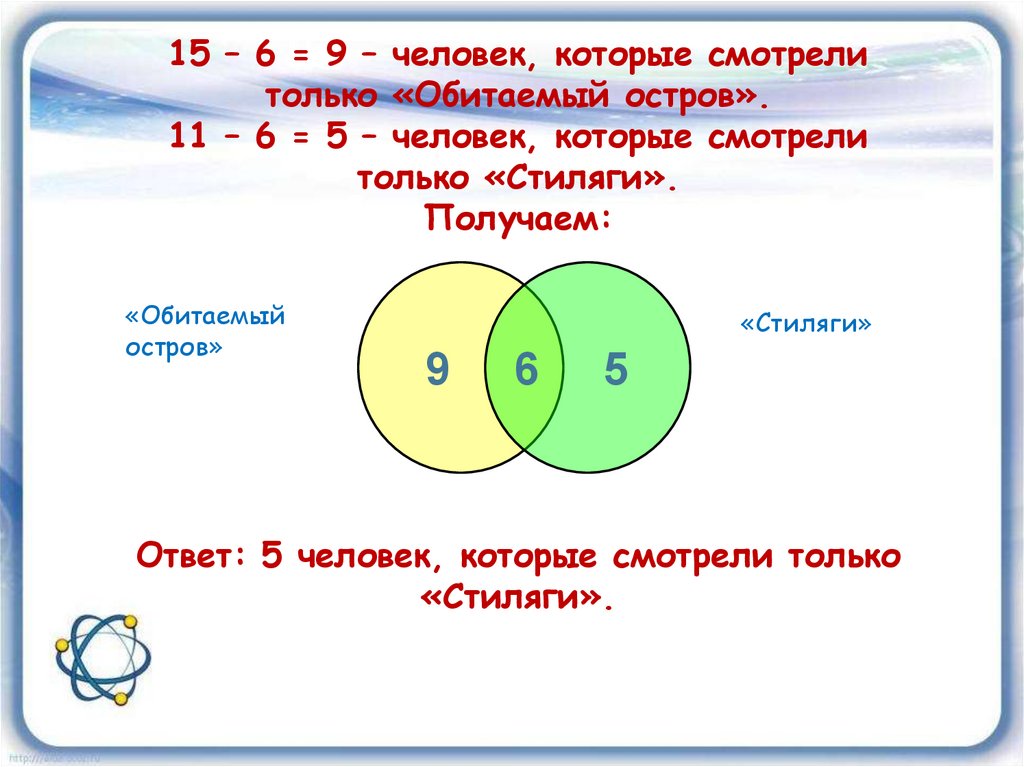
15 – 6 = 9 – человек, которые смотрели
только «Обитаемый остров».
11 – 6 = 5 – человек, которые смотрели
только «Стиляги».
Получаем:
«Обитаемый
остров»
«Стиляги»
9
6
5
Ответ: 5 человек, которые смотрели только
«Стиляги».

5.

Леонард Эйлер
Леонард Эйлер, крупнейший
математик XVIII века, родился в
Швейцарии. В 1727г. по
приглашению Петербургской
академии наук он приехал в
Россию. Эйлер попал в круг
выдающихся математиков,
получил большие возможности для
создания и издания своих трудов.
Он очень много работал и вскоре
стал первым математиком мира.

6.

Леонард Эйлер
Нет учёного, имя которого
упоминалось бы в учебной
литературе по математике
столь же часто, как имя
Эйлера. В Энциклопедии
можно найти сведения о
формулах, уравнениях,
теоремах , которые носят имя
Эйлера.

7.

Леонард Эйлер
Эйлер писал тогда, что «круги
очень подходят для того, чтобы
облегчить наши размышления».
При решении целого ряда задач
он использовал идею
изображения множеств с
помощью кругов и эти круги
получили название «Круги
Эйлера».

8.

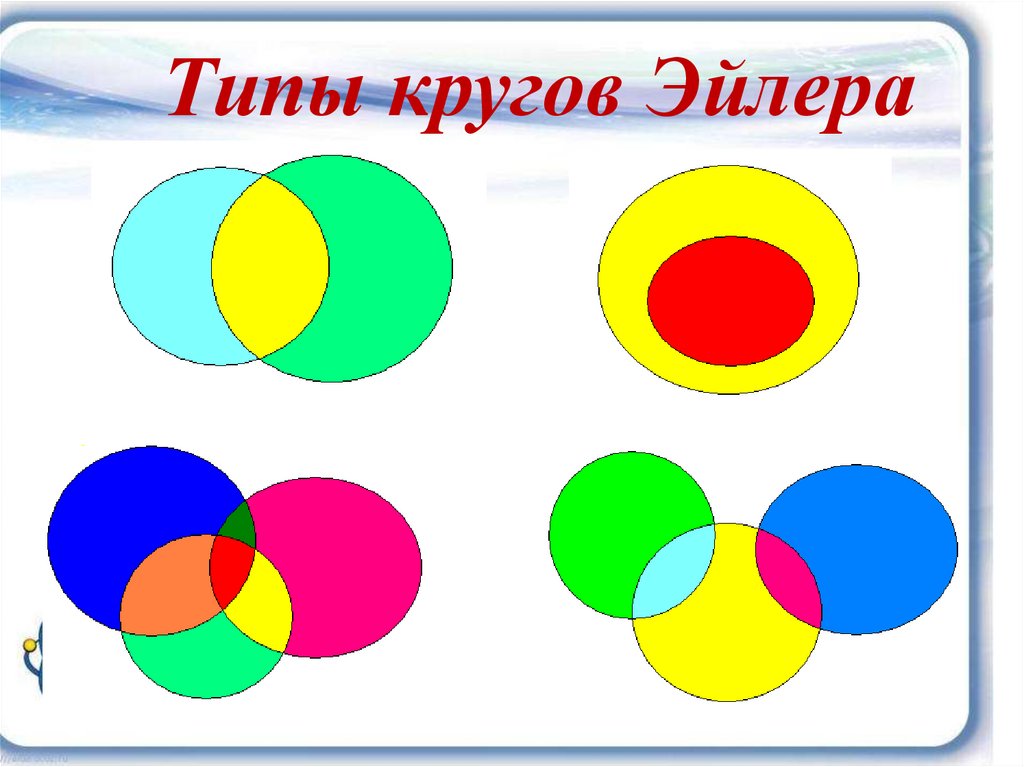
Типы кругов Эйлера

9.

Задача № 2:
Из 100 туристов, отправляющихся в заграничное
путешествие, немецким языком владеют 30 человек,
английским – 28, французским – 42. Английским и
немецким одновременно владеют 8 человек, английским и
французским -10 , немецким и французским – 5, всеми
тремя языками – 3.
Сколько туристов не владеют ни одним языком?
Решение:
Выразим условие задачи графически. Обозначим кругом тех, кто
знает английский, другим кругом – тех, кто знает французский, и
третьим кругом – тех, кто знают немецкий.
немецкий
французский
английский

10.

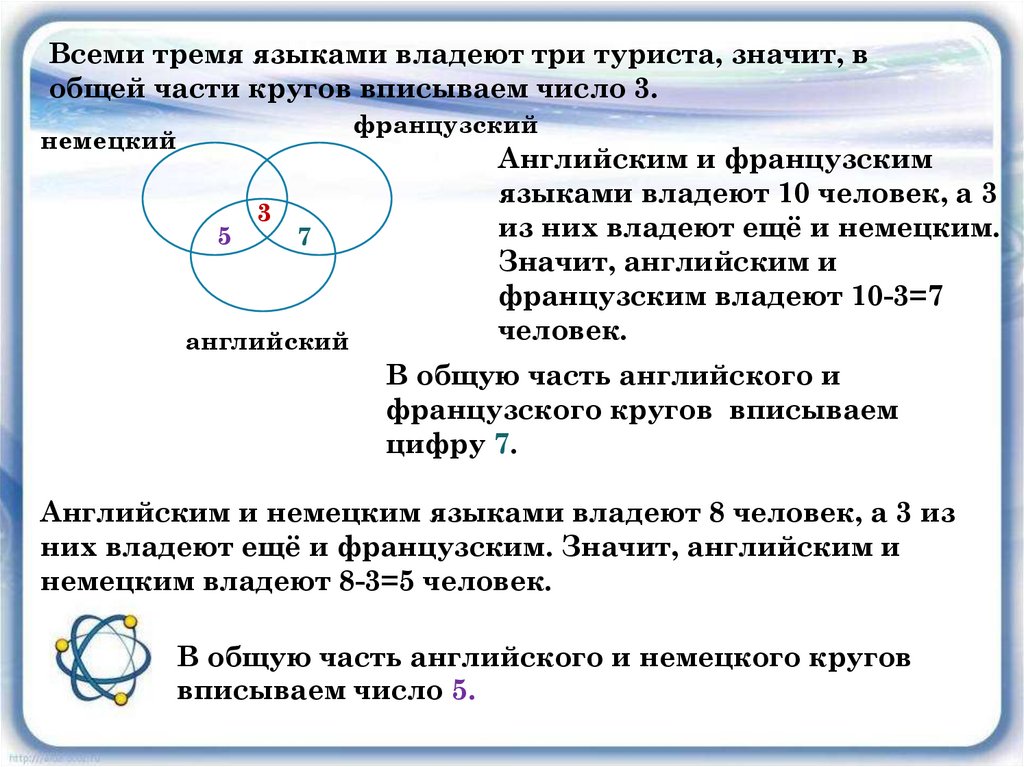
Всеми тремя языками владеют три туриста, значит, в
общей части кругов вписываем число 3.
французский
немецкий
5
3
7
английский
Английским и французским
языками владеют 10 человек, а 3
из них владеют ещё и немецким.
Значит, английским и
французским владеют 10-3=7
человек.
В общую часть английского и
французского кругов вписываем
цифру 7.
Английским и немецким языками владеют 8 человек, а 3 из
них владеют ещё и французским. Значит, английским и
немецким владеют 8-3=5 человек.
В общую часть английского и немецкого кругов
вписываем число 5.

11.

французский
немецкий
20
5
2
3
30
7
13
английский
Немецким и французским
языками владеют 5 человек, а
3 из них владеют ещё и
английским. Значит,
немецким и французским
владеют 5-3=2 человека.
В общую часть немецкого и
французского кругов вписываем
цифру 2.
Известно, что немецким языком владеют 30 человек, но 5+3+2=10 из
них владеют и другими языками, значит, только немецкий знают 20
человек.
Английский язык знают 28 человек, но 5+3+7=15 человек владеют и
другими языками, значит, только английский знают 13 человек.
Французский язык знают 42 человека, но 2+3+7=12 человек владеют
и другими языками, значит, только французский знают 30 человек.
По условию задачи всего 100 туристов. 20+30+13
+5+2+3+7=80 туристов знают хотя бы один язык,
следовательно, 20 человек не владеют ни одним языком.
Ответ: 20 человек.

12.

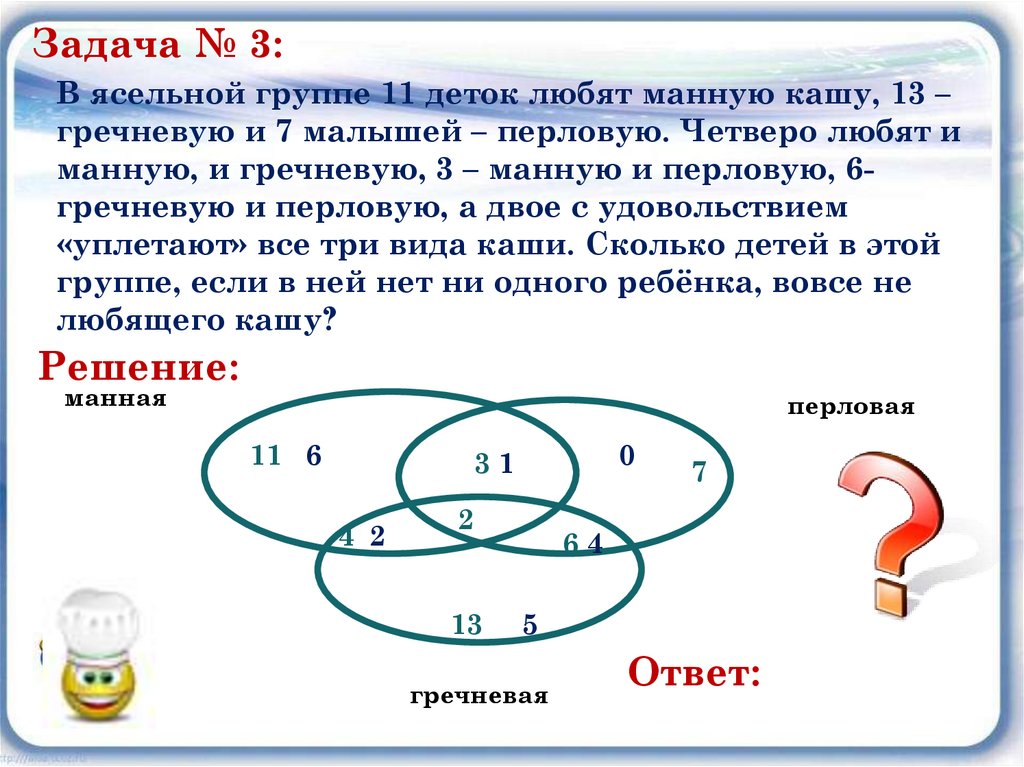
Задача № 3:
В ясельной группе 11 деток любят манную кашу, 13 –
гречневую и 7 малышей – перловую. Четверо любят и
манную, и гречневую, 3 – манную и перловую, 6гречневую и перловую, а двое с удовольствием
«уплетают» все три вида каши. Сколько детей в этой
группе, если в ней нет ни одного ребёнка, вовсе не
любящего кашу?
Решение:
манная
перловая
11 6
0
31
4 2
2
13
7
64
5
гречневая
Ответ:
6+1+2+2+0+4+5=20 ребят

13.

Задача № 4:
У меня жили кролики. 7 из них любили капусту, 6 – морковь,
5 – горох, 4 – капусту и морковь, 3 – капусту и горох, 2 –
морковь и горох, 1 – и капусту, и морковь, и горох. Сколько
кроликов у меня было?
Решение:
капуста
7
морковь
1
43
32
1
5 1
горох
21
6
1
Ответ: 10
кроликов.

14.

Задача № 5:
«Гарри Поттер, Рон и Гермиона»
На полке стояло 26 волшебных книг по
заклинаниям, все они были прочитаны. Из них
4 прочитал и Гарри Поттер, и Рон. Гермиона
прочитала 7 книг, которых не читали ни Гарри
Поттер, ни Рон, и две книги, которые читал
Гарри Поттер. Всего Гарри Поттер прочитал 11
книг. Сколько книг прочитал только Рон?

15.

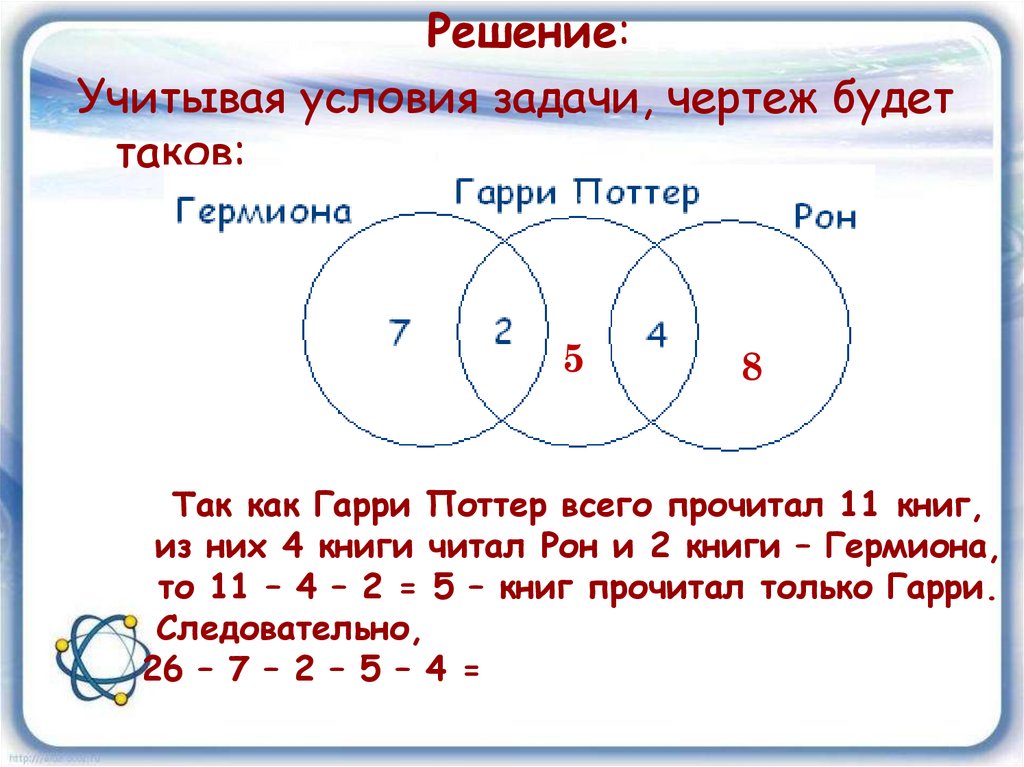
Решение:
Учитывая условия задачи, чертеж будет
таков:
5
8
Так как Гарри Поттер всего прочитал 11 книг,
из них 4 книги читал Рон и 2 книги – Гермиона,
то 11 – 4 – 2 = 5 – книг прочитал только Гарри.
Следовательно,
26 – 7 – 2 – 5 – 4 = 8 – книг прочитал только
Рон.

16.

Задачи для самостоятельного решения:
Задача № 6:
Из 40 опрошенных человек 32 любят
молоко, 21 – лимонад, а 15 – и молоко,
и лимонад. Сколько человек не любят
ни молоко, ни лимонад?
Ответ: 2 человека

17.

Задача для самостоятельного решения:
Задача № 7:
В воскресенье 19 учеников нашего класса
побывали в планетарии, 10 – в цирке и 6 – в
музее. Планетарий и цирк посетили 5
учеников; планетарий и музей – трое, в
цирке и музее был один человек. Сколько
учеников в нашем классе, если никто не
успел посетить все три места, а трое
вообще никуда не ходили?
Ответ: 20 человек

18.

Задача для самостоятельного решения:
Задача № 8:
В детском лагере отдыхало 70 ребят.
Из них 20 занимаются в драмкружке, 32
поют в хоре, 22 увлекаются спортом. В
драмкружке 10 ребят из хора, в хоре 6
спортсменов, в драмкружке 8
спортсменов, а 3 спортсмена посещают и
драмкружок, и хор. Сколько ребят не поют
в хоре, не увлекаются спортом и не
занимаются в драмкружке? Сколько ребят
заняты спортом?
Ответ: 10 ребят, 11 спортсменов.

19.

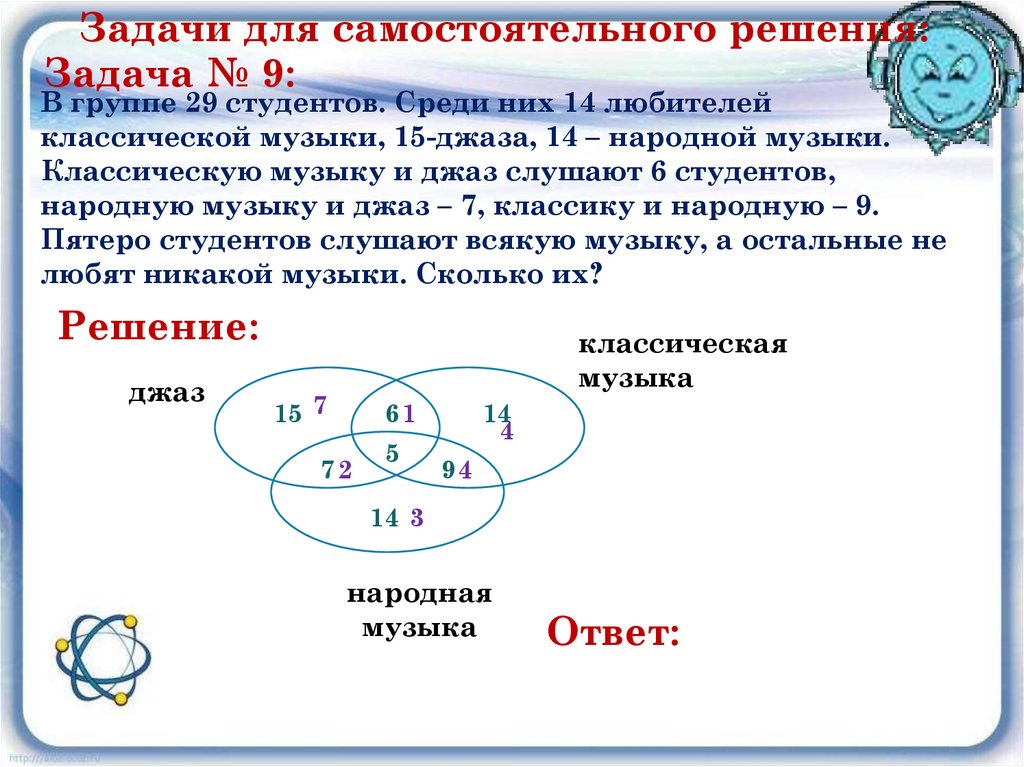
Задачи для самостоятельного решения:
Задача № 9:
В группе 29 студентов. Среди них 14 любителей
классической музыки, 15-джаза, 14 – народной музыки.
Классическую музыку и джаз слушают 6 студентов,
народную музыку и джаз – 7, классику и народную – 9.
Пятеро студентов слушают всякую музыку, а остальные не
любят никакой музыки. Сколько их?
Решение:
джаз
классическая
музыка
15 7
61
72
5
14
4
94
14 3
народная
музыка
Ответ:
29-7-2-1-5-3-4-4=3(человека)
– не любят никакую музыку.

20.

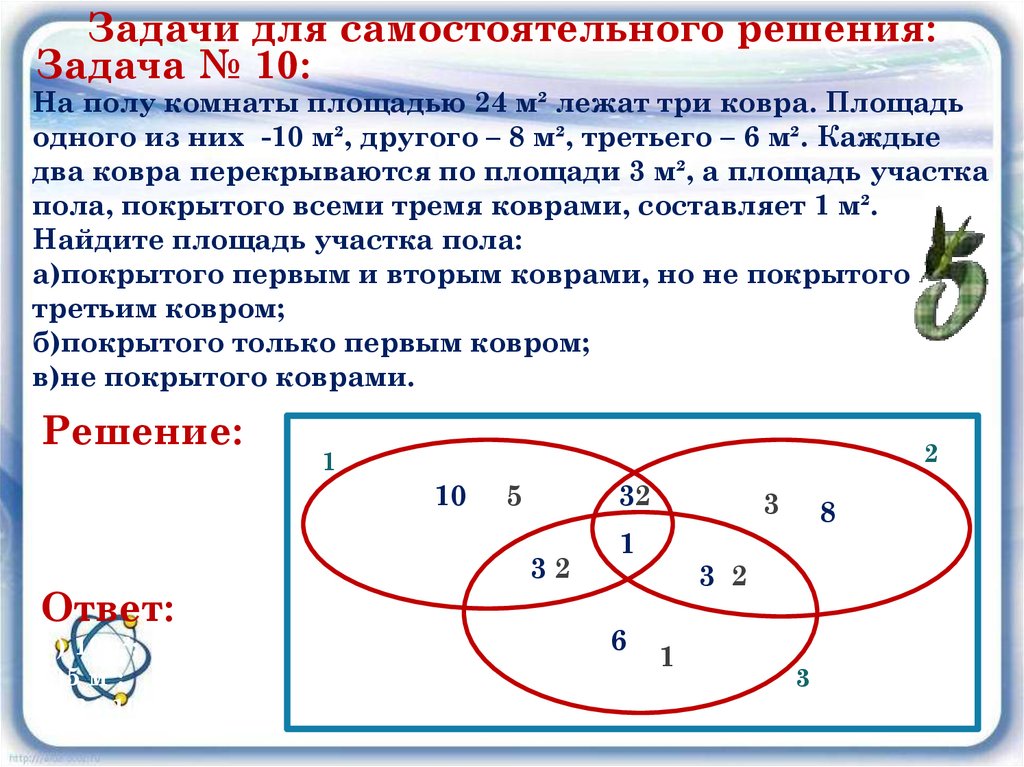
Задачи для самостоятельного решения:
Задача № 10:
На полу комнаты площадью 24 м² лежат три ковра. Площадь
одного из них -10 м², другого – 8 м², третьего – 6 м². Каждые
два ковра перекрываются по площади 3 м², а площадь участка
пола, покрытого всеми тремя коврами, составляет 1 м².
Найдите площадь участка пола:
а)покрытого первым и вторым коврами, но не покрытого
третьим ковром;
б)покрытого только первым ковром;
в)не покрытого коврами.
Решение:
2
1
10
Ответ:
а) 10м²;
б)5 м²;
в) 24-10-5-1=8 м²
5
32
32
3
1
6
8
3 2
1
3

21.

Задача для самостоятельного решения:
Задача № 11:
Из сотрудников фирмы 16
побывали во Франции, 10 – в
Италии, 6 – в Англии. В Англии и
Италии – пятеро, в Англии и
Франции – 6, во всех трёх странах
– 5 сотрудников. Сколько человек
посетили и Италию, и Францию,
если всего в фирме работает 19
человек, и каждый их них
побывал хотя бы в одной из
названных стран?
Ответ: 7 сотрудников

22.

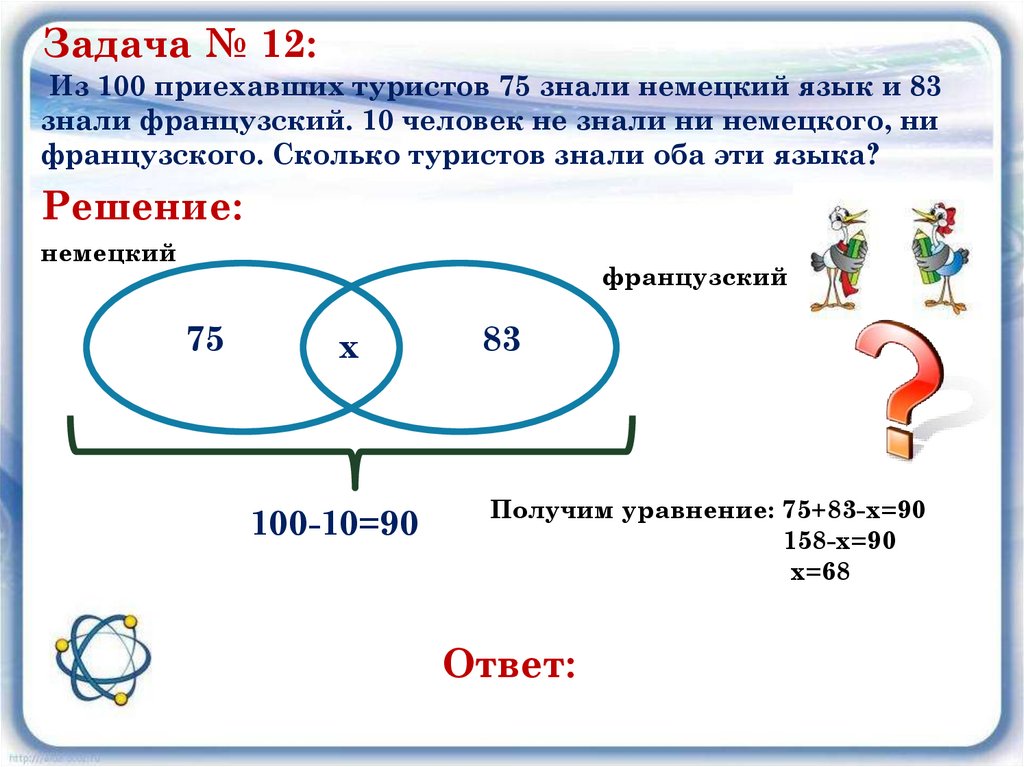
Задача № 12:
Из 100 приехавших туристов 75 знали немецкий язык и 83
знали французский. 10 человек не знали ни немецкого, ни
французского. Сколько туристов знали оба эти языка?
Решение:
немецкий
французский
75
х
100-10=90
83
Получим уравнение: 75+83-х=90
158-х=90
х=68
Ответ:
68 человек знали оба языка

23.

Задача № 13:
В классе 38 человек. Из них 16 играют в
баскетбол, 17 - в хоккей, 18 - в футбол. Увлекаются
только двумя видами спорта – баскетболом и хоккеем
- четверо, баскетболом и футболом - трое, футболом и
хоккеем - пятеро. Трое не увлекаются ни баскетболом,
ни хоккеем, ни футболом. Сколько ребят увлекаются
одновременно тремя видами спорта?
Сколько ребят увлекается лишь одним из этих видов
спорта?

24.

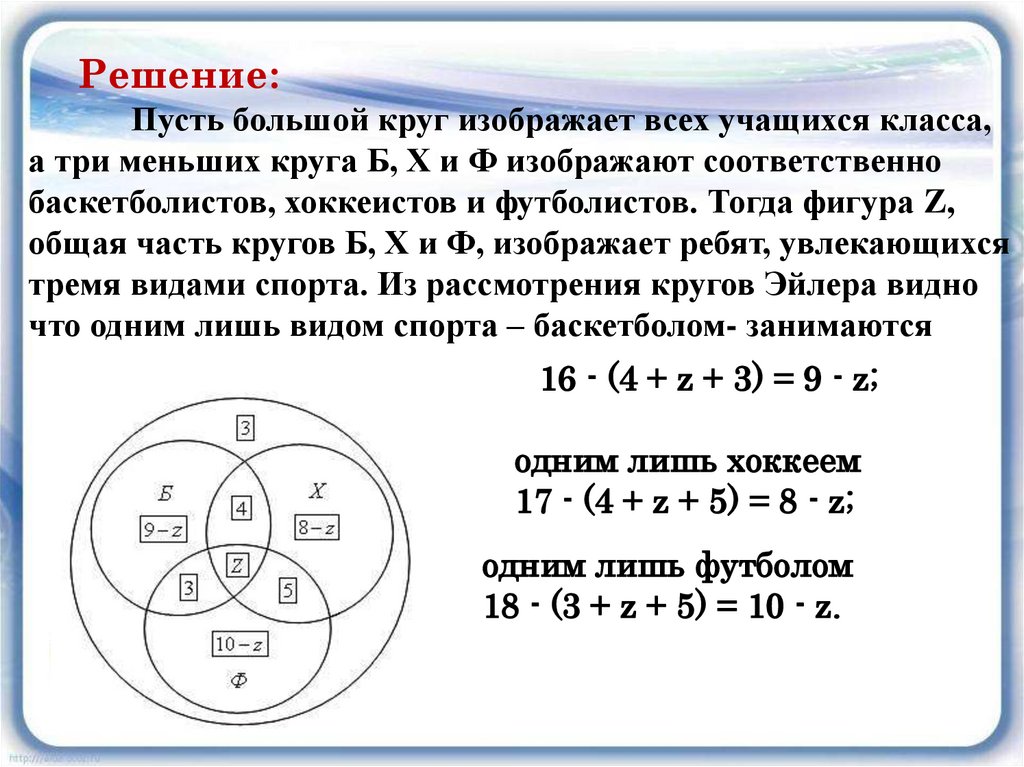
Решение:
Пусть большой круг изображает всех учащихся класса,
а три меньших круга Б, Х и Ф изображают соответственно
баскетболистов, хоккеистов и футболистов. Тогда фигура Z,
общая часть кругов Б, Х и Ф, изображает ребят, увлекающихся
тремя видами спорта. Из рассмотрения кругов Эйлера видно
что одним лишь видом спорта – баскетболом- занимаются
16 - (4 + z + 3) = 9 - z;
одним лишь хоккеем
17 - (4 + z + 5) = 8 - z;
одним лишь футболом
18 - (3 + z + 5) = 10 - z.

25.

Решение:
Составляем уравнение, пользуясь тем, что класс
разбился на отдельные группы ребят; количества ребят в
каждой группе обведены на рисунке рамочками:
3 + (9 - z) + (8 - z) + (10 - z) + 4 + 3 + 5 + z = 38, z = 2.
Таким образом, двое ребят увлекаются всеми
тремя видами спорта.
Складывая числа 9 - z, 8 - z и 10 - z, где z = 2,
найдем количество ребят, увлекающихся лишь
одним видом спорта: 21 человек.
Ответ:
Двое ребят увлекаются всеми тремя видами спорта
Увлекающихся лишь одним видом спорта - 21
человек.