Формирование знаний. Направления в создании ИС (Интеллектуальные компьютерные сети)

1.

ФОРМИРОВАНИЕ
ЗНАНИЙ
ИС-1
2022

2.

НАПРАВЛЕНИЯ В СОЗДАНИИ ИС
(Интеллектуальные компьютерные сети)
• Интеллектуальные информационно-поисковые
системы
• Экспертные системы
• Обучающие системы (тьютеры)
2

3.

ПАРАДИГМЫ РАЗВИТИЯ ИС
• Архитектурные решения на основе
параллельных и асинхронных процессов,
перемещающихся по структуре
взаимосвязанных компьютеров.
• Когнитивная компьютерная графика – наглядное
изображение внутреннего содержания
предмета, абстрактного научного понятия,
гипотезы или теории.
• Создание интеллектуальных гибридных систем
для взаимодействия с пакетами прикладных
программ вычислительной математики.
3

4.

ПАРАДИГМА
• Парадигма — это набор правил, принципов и
понятий которые были сформированы по
отношению к чему-то.
• Парадигма — это давно признанные истины, не
подлежащие никакому сомнению.
• На древнегреческом слово «парадигма»
означает «образец, шаблон, пример».
4

5.

СТРАТЕГИИ ПОЛУЧЕНИЯ ЗНАНИЙ
• Приобретений знаний
• Извлечение знаний
• Формирование знаний
5

6.

ФОРМИРОВАНИЕ ЗНАНИЙ
• Связано с созданием систем автоматического
получения знаний, машинного обучения.
• Предполагается, что система сможет
самостоятельно формировать необходимые
знания на основе имеющегося материала.
• Формирование знаний – задача обработки
данных с целью перехода к базам знаний.
6

7.

БД И БЗ
• БД – накапливаются и хранятся эмпирические
факты из исследуемой предметной области:
Данные
Экспертные заключения
Элементарные высказывания с оценкой
• БЗ - сведения , выражающие закономерности
структуры множества эмпирических фактов,
связанные с прикладным текстом (отношения
эквивалентности и порядка)
7

8.

ОТНОШЕНИЯ ЭКВИВАЛЕНТНОСТИ И
ПОРЯДКА
• Эквивалентности:
Классификация
Диагностика
Распознавание образов
• Порядка:
Шкалирование
Прогнозирование
• Требование интерпретации закономерностей
8

9.

ИНТЕРПРЕТАЦИЯ
ЗАКОНОМЕРНОСТЕЙ
• Лежит в основе правил вхождения объектов в
классы эквивалентности.
• Логические методы:
Эмпирическое предсказание
Индуктивное формирование понятий
Построение квазиаксиоматической теории
• Сложная система организации обучаемых
областей (закономерности описаны
недостаточно точно)
9

10.

ГЕОМЕТРИЧЕСКИЙ ПОДХОД
• Геометрические соотношения между
эмпирическими фактами, отображаемыми
точками в пространстве признаков.
• Главный элемент – объект.
• Основной вид операций – определение
расстояний между объектами в многомерном
пространстве признаков.
• Возможности:
Принцип и критерии более понятны
Представление наглядно
Ошибки при расширении -минимальны
10

11.

ТЕОРЕМА ДЖЕЙМСА-СТЕЙНА
• Развитие теории улучшенного оценивания
• Математики Джеймс и Стейн
• 50-е годы ХХ века
• Оценки Джеймса – Стейна и другие улучшенные
оценки нашли применение в
эконометрике и в задачах, связанных с
обработкой сигналов.
• Даже для близких критериев качества методы,
оптимальные для одного критерия , могут
оказаться недопустимыми для другого и
наоборот.
11

12.

ПРОБЛЕМА ГЕОМЕТРИЧЕСКОГО
ПОДХОДА
• Какие признаки и какую меру выбрать для
определения расстояний между объектами
• Задача: Подбор взвешенной метрики с
использованием логики и обучающей
информации или оцифровка переменных,
основанная на максимизации статистического
критерия.
12

13.

ДВА ПОДХОДА
• Традиционные методы анализа многомерных
данных: представление об общем пространстве
признаков для всех объектов и об одинаковой
мере , применяемой для оценки их сходства или
различия.
• Системы надкибернетического уровня
сложности: каждый объект следует
рассматривать как самостоятельный
информационный факт (совокупность
зафиксированных значений признаков),
имеющий ценные уникальные особенности.
13

14.

МЕТОД ЛОКАЛЬНЫХ ГЕОМЕТРИЙ
Конструирование собственного пространства
признаков и нахождение индивидуальной меры,
определяющих иерархию его сходства с другими
объектами в заданном контексте (локальное
преобразование пространства признаков).
Например, в случае бинарных признаков это
может быть локальная взвешенная метрика
Хэмминга.
14

15.

ЛОКАЛЬНАЯ ВЗВЕШЕННАЯ МЕТРИКА
ХЭММИНГА
• Вес Хэмминга вектора v, обозначаемый как w(v),
определяется как число ненулевых компонент этого
вектора.
• Расстояние Хэмминга между двумя векторами v1 и
v2 равно числу компонент, которыми они отличаются:
W (v1-v2).
• Если v1 и v2 являются кодовыми словами линейного
кода, то разность также должна быть кодовым
словом, т.к. множество всех кодовых слов есть
векторное пространство. Следовательно, расстояние
между двумя кодовыми векторами равно весу
некоторого третьего кодового вектора, и
минимальное расстояние для линейного кода равно
минимальному весу его ненулевых векторов.
15

16.

ОТНОШЕНИЯ ЭКВИВАЛЕНТНОСТИ
• К любому объекту привязан набор различных
локальных метрик.
• Каждый объект может интерпретироваться как
самостоятельный линейный классификатор с
некоторым набором свойств
• Отношения между объектами выражаются
матрицей удаленности (требование
симметричности может не выполняться)
16

17.

На рисунке представлены изображения лиц 16
людей. Эти люди разбиты на два класса. Задача:
найти закономерности такого разбиения.
17

18.

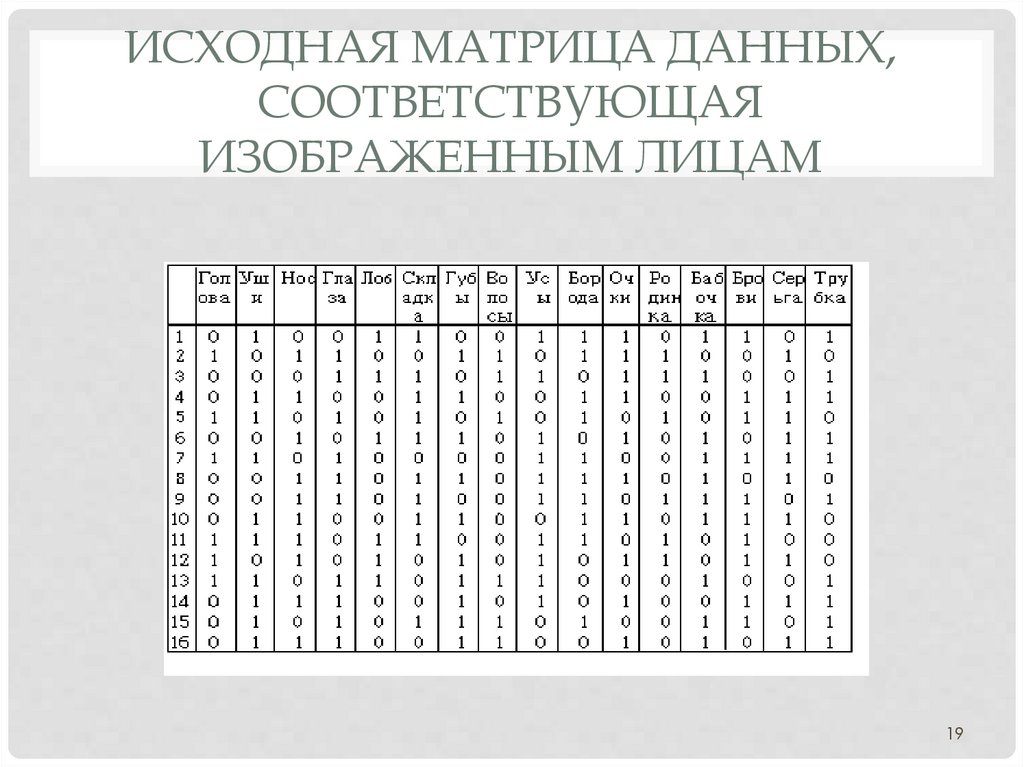
Выделены бинарные признаки, характеризующие
изображенные лица:
голова - круглая - 1, овальная - 0;
уши - оттопыренные - 1, прижатые - 0;
нос - круглый - 1, длинный - 0;
глаза - круглые - 1, узкие - 0;
лоб - с морщинами - 1, без морщин - 0;
складка - носогубная складка есть - 1, складки нет - 0;
губы - толстые - 1, тонкие - 0;
волосы - есть - 1, нет - 0;
усы - есть - 1, нет - 0;
борода - есть - 1, нет - 0;
очки - есть - 1, нет - 0;
родинка - родинка на щеке есть - 1, родинки нет - 0;
бабочка - есть - 1, нет - 0;
брови - подняты кверху - 1, опущены книзу - 0;
серьга - есть - 1, нет - 0;
трубка - курительная трубка есть - 1, нет - 0.
18

19.

ИСХОДНАЯ МАТРИЦА ДАННЫХ,
СООТВЕТСТВУЮЩАЯ
ИЗОБРАЖЕННЫМ ЛИЦАМ
19

20.

ОБРАБОТКА
1.
2.
3.
4.
5.
6.
7.
в исходном пространстве признаков объекты разных классов
перемешаны друг с другом.
дискриминантный анализ привел к положительному эффекту
разделения классов (применялась версия дискриминантного
анализа с использованием процедур последовательного
увеличения и уменьшения группы признаков).
Получена дискриминантная функция
Дискриминантная функция обеспечивает полное разделение
классов w1 и w2. Если стремиться только к формальному
эффекту, то на таком результате разделения классов можно
остановиться.
Однако в данном случае достигнутому формальному эффекту в
слабой степени сопутствует формирование новых знаний о
структуре анализируемых данных.
Единственное, что можно сказать - это перечислить признаки и
веса, с которыми они вошли в линейную дискриминантную
функцию.
Неизвестным остается внутреннее строение классов и данных в
целом, которое может быть достаточно интересным и раскрытие
которого может давать качественно новую информацию.
20

21.

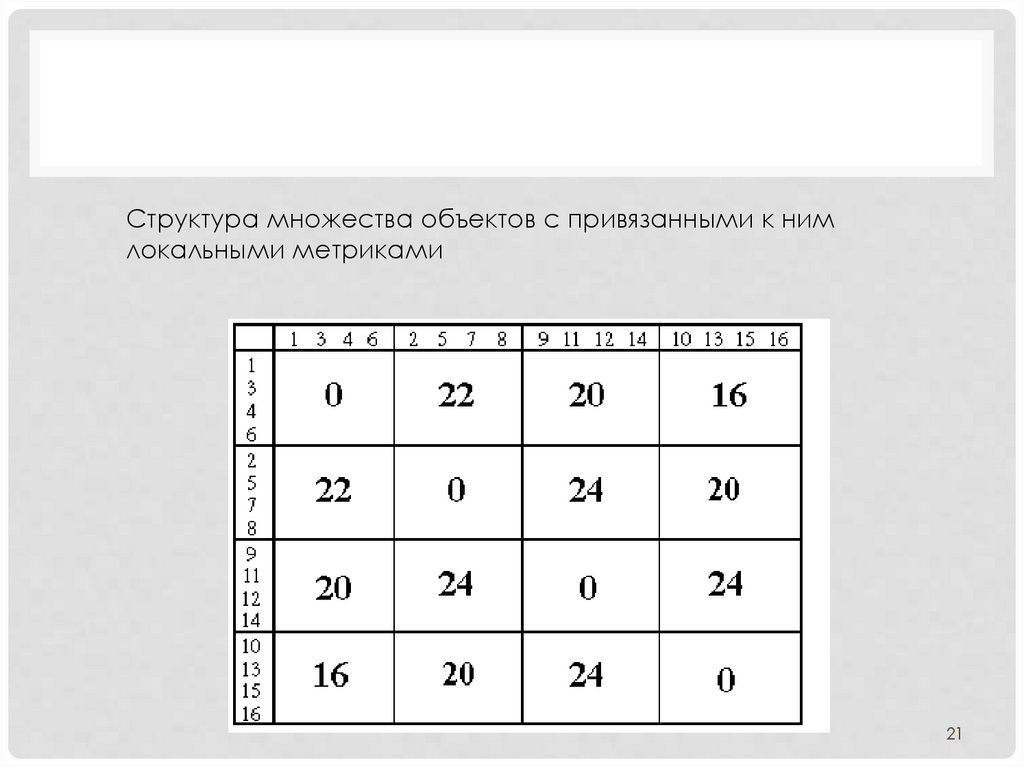
Структура множества объектов с привязанными к ним
локальными метриками
21

22.

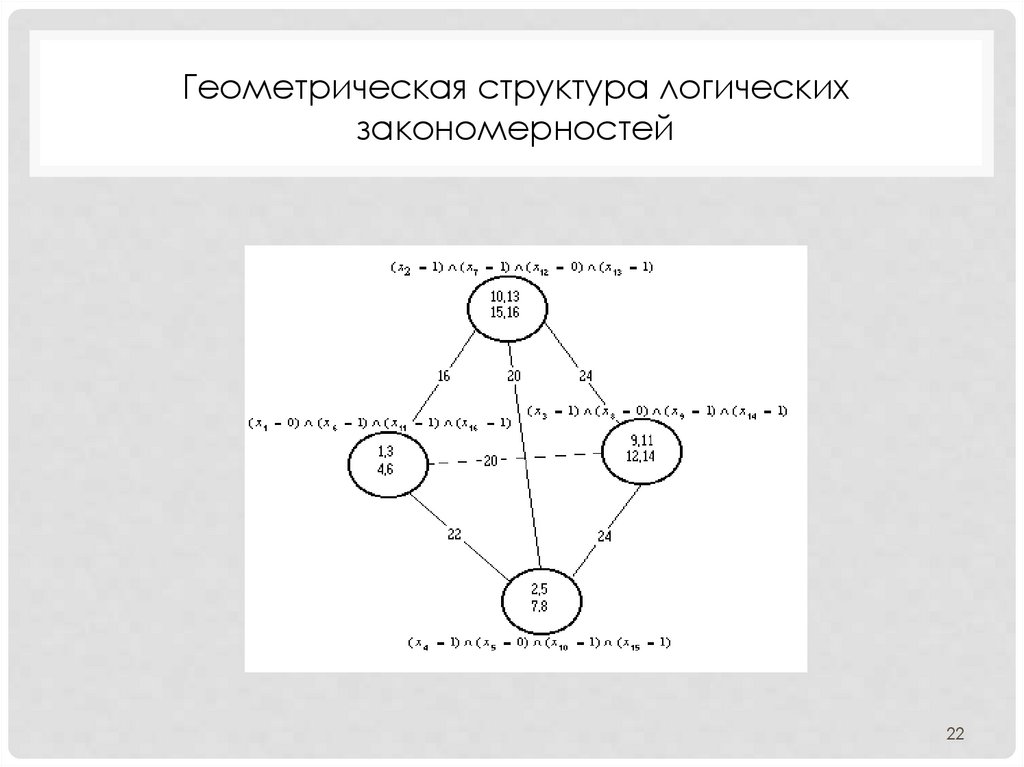
Геометрическая структура логических
закономерностей
22

23.

ВОЗМОЖНОСТЬ ИСПОЛЬЗОВАНИЯ
ВИЗУАЛЬНЫХ ОТОБРАЖЕНИЙ
• Возможность обоснования принятия решения о
принадлежности неизвестного объекта какому либо
классу эквивалентности путем получения ответов на
вопросы:
Что общего у данного объекта с другим
объектом/группой?
Чем отличается данный объект от другого
объекта/группы?
• Ответы – в виде пересечения.
• Совокупность ответов обладает полиморфностью.
• Объяснение принятых решений посредством
аргументации.
23

24.

ВИЗУАЛЬНОЕ ПРЕДСТАВЛЕНИЕ
• Геометрическое изображение структуры
множества объектов с оптимизированными
описаниями посредством локальных метрик
дает наглядное визуальное представление об ее
особенностях, что помогает формированию
результирующего правила вывода
• Представляются возможности применения
описанного подхода для анализа совокупности
объектов при отсутствии информации об их
группировании в какие-либо классы.
24