Перпендикулярность плоскостей

1.

ПЕРПЕНДИКУЛЯРНОСТЬ
ПЛОСКОСТЕЙ
ВЫПОЛНИЛИ:
БУШУЕВА ВАЛЕРИЯ
ЗАЙЦЕВА СВЕТЛАНА
ПИХЛАЯ ПОЛИНА

2.

3.

ПЕРПЕНДИКУЛЯРНОСТЬ ПЛОСКОСТЕЙ
Определение 1
Углом между плоскостями называется
минимальный из двугранных углов,
образованных этими плоскостями.
Определение 2
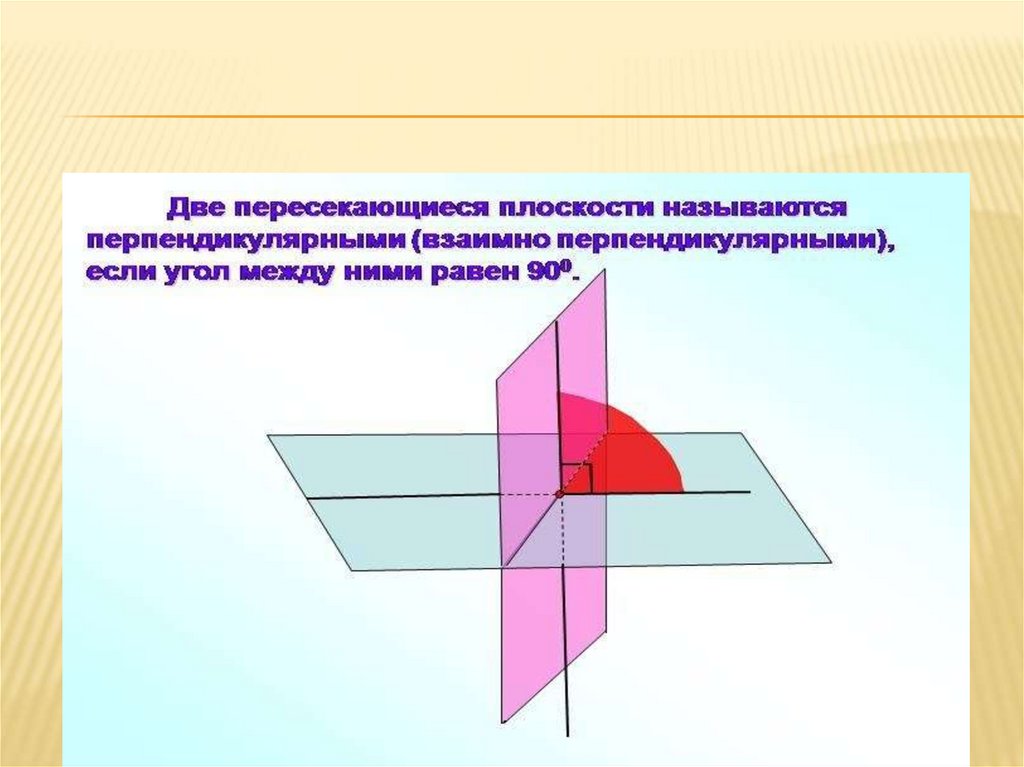
Две пересекающиеся плоскости называются
перпендикулярными, если угол между этими
плоскостями равен 90∘

4.

ПЕРПЕНДИКУЛЯРНОСТЬ ПЛОСКОСТЕЙ
Признак перпендикулярности двух плоскостей
Теорема 1
Если прямая плоскости перпендикулярна другой
плоскости, то эти плоскости перпендикулярны друг
другу.
Из этой теоремы следует следующая теорема.
Теорема 2
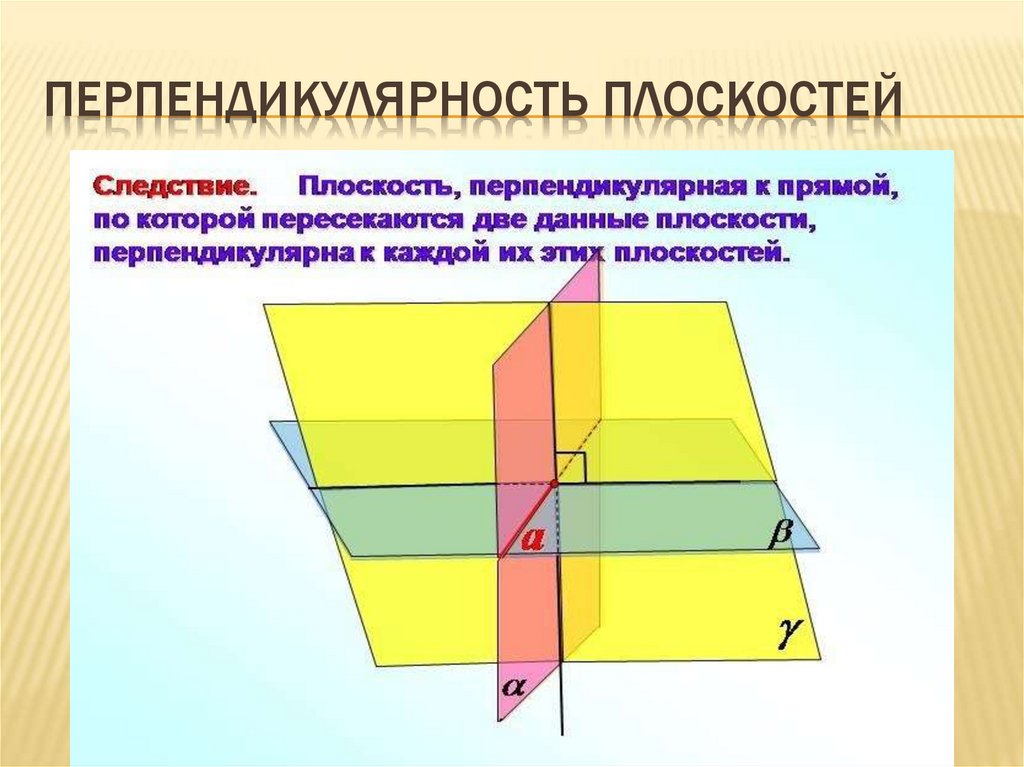
Если плоскость перпендикулярна прямой, по которой
пересекаются две другие плоскости, то она
перпендикулярна и этим плоскостям.

5.

ПЕРПЕНДИКУЛЯРНОСТЬ ПЛОСКОСТЕЙ

6.

ПЕРПЕНДИКУЛЯРНОСТЬ ПЛОСКОСТЕЙ
1 ВАРИАНТ Даны две взаимно
перпендикулярные плоскости а и β,
пересекающиеся по прямой с. Из точки А
плоскости β проведен перпендикуляр АС к
плоскости с. Доказать, что эта прямая лежит в
данной плоскости.

7.

ПЕРПЕНДИКУЛЯРНОСТЬ ПЛОСКОСТЕЙ
2 ВАРИАНТ

8.

ПЕРПЕНДИКУЛЯРНОСТЬ ПЛОСКОСТЕЙ
1 ВАРИАНТ
Доказательство:
Рассмотрим треугольник АВС.
Он является прямоугольным
с прямым углом АСВ. Следовательно, <ABC ≠ 90º.
Но, с другой стороны, <АВС является линейным углом
двугранного угла, образованного этими плоскостями.
То есть двугранный угол, образованный этими
плоскостями не равняется 90 градусам. Получаем, что
угол между плоскостями не равен 90°. Противоречие.
Следовательно, АС лежит в плоскости В.

9.

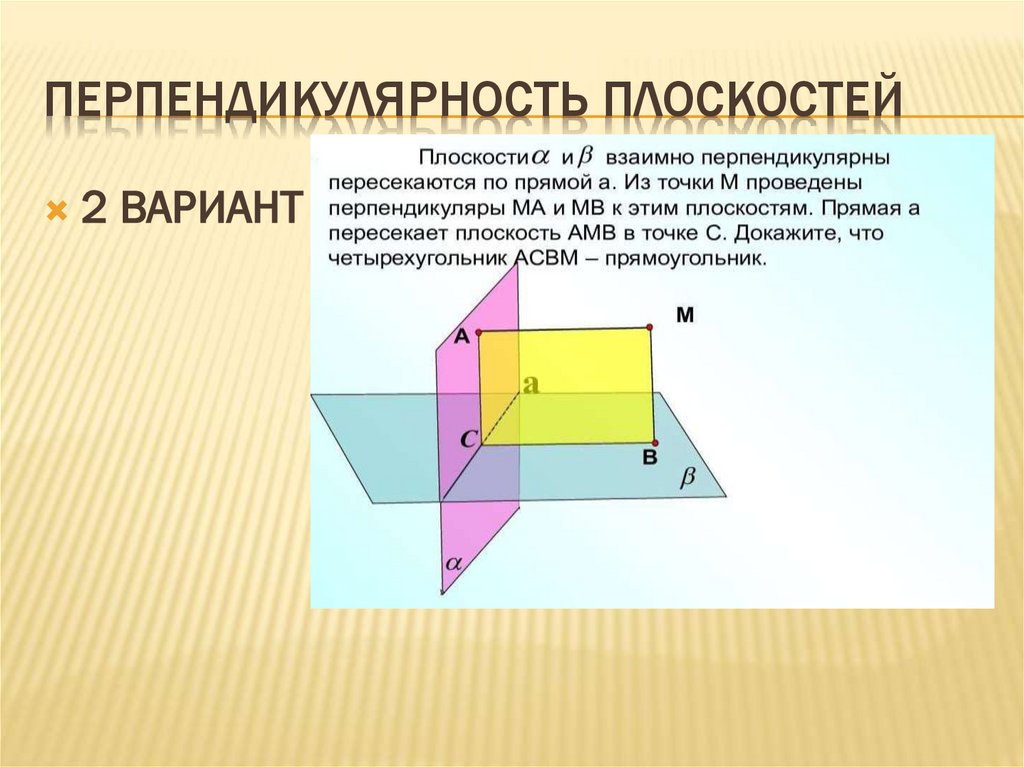
ПЕРПЕНДИКУЛЯРНОСТЬ ПЛОСКОСТЕЙ
2 ВАРИАНТ
Так как MB ⊥ β, МА ⊥ α, то MA ⊥ a, MB ⊥ a,
следовательно, а ⊥ АМВ, значит, а ⊥ СВ, а ⊥
СА=>∠ВСА=90°
2) т. к. МА ⊥ α, МВ ⊥ β, то МА ⊥ АС, МВ ⊥ ВС,
=>∠МАС=МВС=90° =>АСВМ-прямоугольник