Сортировка. Методы программирования

1.

Методы программирования
Лекция 2. Сортировка.
Лектор: Крючков Алексей Вячеславович

2.

Изучаемые вопросы
3.1. Описание алгоритмов сортировки
(продолжение)
3.2. Оценка методов сортировки
Крючков А.В.
2

3.

Введение
Цель курса – ознакомление обучающихся с различными
методами сортировки и поиска и формирование навыка
их практического применения.
В данной лекции мы продолжаем описывать различные
алгоритмы сортировки.
В тестах и на экзамене будут вопросы по всем описанным
в лекциях методах.
Крючков А.В.
3

4.

Вопрос 1. Описание алгоритмов сортировки
На предыдущем лекционном мероприятии мы
рассмотрели 6 методов сортировки. В данной лекции
нам предстоит узнать ещё о 12.
Напоминаю, что методы рассматриваются
применительно к одномерным массивам,
расположенным в памяти ЭВМ. На более сложных
структурах данных Вы будете применять полученные
знания самостоятельно.
Крючков А.В.
4

5.

Вопрос 1.1. Гномья сортировка
Гномья сортировка получила своё название в связи с тем, что
данный её метод основан на технике, которая похожа на
сортировку голландским садовым гномом (нидерл. tuinkabouter)
линию цветочных горшков.
Гном смотрит на два соседних садовых горшка: предыдущий и
следующий (в нашем случае элементы одномерного массива) – и,
если они значимая часть предыдущего, текущего и последующего
«горшков» упорядочены по возрастанию, то он перешагивает их, а
также двигается на один горшок вперёд, чтобы повторить
процедуру. В противном случае, гном меняет горшки местами и
двигается на один шаг назад.
Крючков А.В.
5

6.

Вопрос 1.1. Гномья сортировка. Реализация
При реализации программисты часто применяют не три, как я
сказал выше, а только 2 соседних элемента в наборе данных. В
этом случае первые два элемента сравниваются. Если они
упорядочены (последующий больше предыдущего), программа
переходит к работе с 3-4 элементами и т.д.
Т.к. наборы данных ограничены, в алгоритме необходимы
граничные условия:
- первый элемент в наборе (нет предыдущего горшка) – шаг
вперёд;
- последний элемент в наборе (нет следующего горшка) – конец
процесса.
Крючков А.В.
6

7.

Вопрос 1.1. Гномья сортировка. Улучшение
Улучшение алгоритма связано с запоминаем места в наборе
данных (индекса массива), после которого элементы уже
упорядочены.
Тогда после сортировки начального подмассива можно завершить
процесс.
Беда этого улучшения в том, что программе изначально
неизвестно, в каком месте массива начинаются уже
отсортированные элементы. Поэтому либо необходимо в одном
цикле проверять отсортированность элементов в конце набора
данных, либо не применять это улучшение. В обоих случаях число
иттераций и сравнений возрастает.
Крючков А.В.
7

8.

Вопрос 1.1. Гномья сортировка. Оценка
В лучшем и в худшем случае число
сравнений будет равно n2, где n – число
элементов массива.
Крючков А.В.
8

9.

Вопрос 1.2. Сортировка выбором
В классическом смысле применения
данного алгоритма существует два
варианта его реализации, связанных с
направлением поиска:
- ориентация на минимальный по
значению элемент в массиве;
- ориентация на максимальный по
значению элемент.
Крючков А.В.
9

10.

Вопрос 1.2. Сортировка выбором. 1-й вариант
Перебор, начинающийся с первого элемента, направлен на то,
чтобы найти минимальный по значению элемент в массиве. На
это направлен первый проход.
Значение найденного минимального элемента помещается в
первый элемент массива, а значение первого в ячейку памяти с
номером минимального (меняем их местами).
На втором проходе процесс повторяется, начинаясь со второго
элемента. И так далее, пока весь массив не будет отсортирован.
Крючков А.В.
10

11.

Вопрос 1.2. Сортировка выбором. 2-й вариант
Перебор начинается с первого элемента.
Он направлен на то, чтобы найти максимальный по значению
элемент в массиве в первом проходе.
Значение найденного максимального элемента помещается в
последний элемент массива, а значение последнего в ячейку
памяти с номером максимального (смена мест).
На втором проходе процесс повторяется, начинаясь с первого
элемента и заканчиваясь на предпоследнем. И так далее, пока
весь массив не будет отсортирован.
Крючков А.В.
11

12.

Вопрос 1.2. Сортировка выбором. Оценка
В лучшем и в худшем случае число
сравнений будет равно n2, где n – число
элементов массива.
Крючков А.В.
12

13.

Вопрос 1.3. Пирамидальная сортировка
Данный метод получил своё название по
причине аналогии структуры данных,
получаемой из набора данных, с пирамидой.
Он основан на представлении массива в виде
двоичного дерева. Двоичным дерево (граф в
математическом смысле) является потому, что
из каждой вершины выходит по 2 ребра.
Иногда число элементов в наборе данных не
позволяет получить на «выходе» по 2 ребра
для всех вершин дерева. В этом случае одна
вершина имеет на выходе только одно ребро,
или не иметь их вообще.
Крючков А.В.
13

14.

Вопрос 1.3. Пирамидальная сортировка
Первый шаг алгоритма
На первом шаге алгоритма сортировки строится
двоичное дерево. Массив при этом остаётся без
изменений. Правила построения дерева таковы.
1. Первый элемент – корень дерева.
2. Следующие 2 элемента – первый уровень дерева.
3. Следующие 4 элемента – второй уровень дерева.
4. Следующие 8 элемента –третий уровень дерева и т.д.
Четвёртый уровень дерева будет содержать уже 16
элементов. При величине массива в 24 элемента
последние 2 вершины графа останутся без рёбер.
Крючков А.В.
14

15.

Вопрос 1.3. Пирамидальная сортировка
Второй шаг алгоритма
На втором шаге сортировки выполняется
обмен элементов массива между собой с
целью переместить наибольший по значению
элемент в вершину дерева. Это действие
называется просеиванием. Для этого
выполняются шаги в следующем порядке.
Пусть n – число элементов массива, и
нумерация в нём начинается с 1.
Крючков А.В.
15

16.

Вопрос 1.3. Пирамидальная сортировка
Второй шаг. Просеивание. Шаги 1, 2
1. Последовательно выбираются ветви
дерева. Для массива с рис.3 это набор
элементов с номерами 1, 2, 4, 8 или 9, и т.д.
(i, 2i, 4i, 8i или 8i + 1 или 1,15,13,9).
2. Так как 1 меньше 15, то элемент массива с
номером 1 (равный 1) перемещается на
позицию элемента с номером 9 (равным 9).
Остальные элементы перемещаются «вверх» по дереву: элемент с
номером 2 (равный 15) становится первым, элемент с номером 4
(равный 13) становится вторым, элемент с номером 9 (равный 9)
становится четвёртым.
Крючков А.В.
16

17.

Вопрос 1.3. Пирамидальная сортировка
Второй шаг. Просеивание. Шаги 3, 4
3. Дерево на основе изменённого массива
перестраивается
4. Процесс повторяется для всех
возможных ветвей дерева до тех пор, пока
в вершине дерева не будет находится
самый большой по значению элемент.
Крючков А.В.
17

18.

Вопрос 1.3. Пирамидальная сортировка
Третий шаг алгоритма
1. Полученный в результате просеивания
максимальный элемент, стоящий первым в
массиве, перемещается в его конец (выполняется
присваивание mass [n-1] = mass [0]). Все остальные
элементы перемещаются на 1 влево (на рис.
жёлтые).
2. Создаётся копия массива, содержащая (n – 1)
элементов с индексами от 0 до (n – 1).
3. Для неё выполняются шаги 1 и 2 описанного
алгоритма: выстраивается новое дерево (на рис. на
1 вершину меньше) и проводится просеивание.
При достижении размера копии массива 1 происходит завершение.
Крючков А.В.
18

19.

Вопрос 1.3. Пирамидальная сортировка. Оценка
В лучшем и в худшем случае число
сравнений будет равно n*log2(n), где n
– число элементов массива.
Крючков А.В.
19

20.

Вопрос 1.4. Быстрая сортировка
В основу алгоритма данного метода
сортировки положен принцип
разбиения массива на 2 части с
помощью некоторого элемента
массива, который называется пивотом.
Выбрав его положение следует в левую
часть перемещать элементы, значения
которых меньше его, а в правую часть –
элементы, значения которых больше
или равны его значению.
Крючков А.В.
20

21.

Вопрос 1.4. Быстрая сортировка
В случае если пивот выбирается произвольно, алгоритм
называют рандомизированным. Выбор пивота важен для
получения приемлемых оценок итоговой сложности алгоритма
по данному методу сортировки, но обоснованных
предложений по тому, как именно это делать нет.
В простейшем случае пивотом может быть первый или
последний элементы массива. Получив 2 половинки массива,
мы для каждой из них применяем ту же схему: выбор пивота и
перемещение меньших по значению элементов левее его и
больших или равных ему по значению элементов – правее.
Крючков А.В.
21

22.

Вопрос 1.4. Быстрая сортировка. Оценка
В лучшем случае число сравнений
равно n*log2(n) .
В худшем случае число сравнений
будет равно n2.
Крючков А.В.
22

23.

Вопрос 1.5. Сортировка слиянием
Метод основан на разбиении массива
на множество частей, содержащих
только 1 элемент. Такие массивы
считаются отсортированными. Если
размерность массива n, то мы имеем
при разбиении n подмассивов.
В алгоритме сортировки по данному
методу необходимо будет выполнить
минимум (n/2 + 1) проходов.
Крючков А.В.
23

24.

Вопрос 1.5. Сортировка слиянием
Первый проход
1. Если исходный массив (подаваемый на вход
программы) состоит из одного значимого элемента
– следует завершить работу.
2. Если значимых элементов больше одного – из
элементов массива следует получить равное
размерности массива число подмассивов, каждый
из которых состоит из одного значимого элемента.
3. Выполнить процедуру попарного слияния
соседних подмассивов: в полученном подмассиве
из двух элементов слева будет находится меньший.
4. Если число элементов нечётное, то последний
подмассив переходит на следующий проход без
слияния.
Крючков А.В.
24

25.

Вопрос 1.5. Сортировка слиянием
Второй и следующие проходы
1. Формируется массив размером, равным
сумме размеров подмассивов, участвующих
в слиянии.
2. Попарно сравниваются элементы
массивов. Самый маленький по значению
элемент сливающихся подмассивов
помещается в первый элемент
формируемого.
3. Если есть непарные подмассивы, то они
переносятся на следующий проход как есть
Крючков А.В.
25

26.

Вопрос 1.5. Сортировка слиянием
Естественное неймановское слияние
1. Всего используется три магнитные ленты — основная, на которой записаны неотсортированные данные
и две вспомогательные.
2. Данные последовательно считываются с основной ленты.
3. Пока последовательно считываемые данные представляют из себя упорядоченный подмассив, они
переписываются на одну из вспомогательных лент.
4. Как только завершается очередной отсортированный подмассив (т.е. на основной ленте встречается
элемент, меньший чем предыдущий), на вспомогательной ленте ставится указатель (конец подмассива)
и происходит переключение на другую вспомогательную ленту.
5. Пункты 2-4 повторяются снова, только данные переносятся уже на другую вспомогательную ленту. При
завершении очередного упорядоченного подмассива на основной ленте происходит поочерёдное
переключение то на одну вспомогательную ленту, то на другую.
6. Когда все данные с основной ленты считаны, происходит обработка вспомогательных лент.
7. С обеих вспомогательных лент поочерёдно считываются данные.
8. При этом очередные данные с двух лент сравниваются между собой. По результатам сравнения на основную ленту записывается меньший
элемент из пары.
9. Так как границы массивов на вспомогательных лентах отмечены указателями, считывание и сравнение происходит только в пределах
отсортированных подмассивов.
10.Если на одной из вспомогательных лент закончились элементы очередного подмассива, то с оставшейся ленты остаток подмассива просто
переносится на основную ленту.
11.Повторяем весь процесс заново до тех пор, пока данные на основной ленте не будут собой представлять полностью упорядоченный массив.
Крючков А.В.
26

27.

Вопрос 1.5. Сортировка слиянием. Оценка
Во всех случаях в методе будет выполнено
n* log2(n) сравнений.
Есть ещё ряд алгоритмов сортировки
слиянием, но их рассмотрение лежит за
пределами данного курса.
Крючков А.В.
27

28.

Вопрос 1.6. Сортировка подсчетом
В данном алгоритме сортировки используется некий диапазон чисел
сортируемого массива для определения количества совпадающих
элементов в нём. Предполагается, что массив или список содержат
только числа.
Если метод применяется для списков строк, то для них следует задать
числовые ключи и работать с ними. Если возможные значения
сортируемых чисел попадают в заданный диапазон, и при этом сам
диапазон достаточно мал по сравнению с размером массива, то данный
алгоритм целесообразно применять. В противном случае следует
использовать другие методы.
Примером удачного выбора данного метода является сортировка
подсчётом массива, содержащего миллион натуральных чисел меньших
1000.
Крючков А.В.
28

29.

Вопрос 1.6. Сортировка подсчетом. Реализация
Линейный вариант
Массив из n элементов (n целых чисел в диапазоне от 0 до
k-1, где k ∈ N, N – множество натуральных чисел, n ≥ k).
Шаг первый. Создадим «безразмерный» вспомогательный
массив (длина его 0 или 1). Изначально k неизвестно. Его
ищем на шаге два.
Шаг второй. Выполняем первый проход по исходному
массиву. Если нам попалось число k, то считаем, что
размер вспомогательного массива равен k. После этого
переходим к шагу три. Если попалось число меньшее k, то
увеличиваем число элементов во вспомогательном
массиве до размера этого числа. Выполняем операцию
пока не встретится k и переходим шагу 3.
Шаг третий. Заполняем вспомогательный массив нулями.
Крючков А.В.
29

30.

Вопрос 1.6. Сортировка подсчетом. Реализация
Линейный вариант
Шаг четвёртый. Проходим по исходному массиву сначала
до конца. Число, которое встречается в исходном массиве,
является индексом вспомогательного массива,
соответствующий элемент которого увеличивается на 1.
После выполнения данного шага вспомогательный массив
будет содержать в каждом из элементов количество
каждого из натуральных чисел в диапазоне от 0 до k-1.
Шаг пятый. Проходя по исходному массиву слева направо,
вписываем номера элементов вспомогательного массива в
исходный то количество раз, которое записано в
соответствующем элементе вспомогательного.
Крючков А.В.
30

31.

Вопрос 1.6. Сортировка подсчетом. Оценка
Во всех случаях в методе будет
выполнено (n + k) сравнений.
Крючков А.В.
31

32.

Вопрос 1.7. Блочная сортировка
Необходимо разбить массив на ряд блоков
(или карманов), размер которых
определяется характером значений в
массиве.
В одном предельном случае, аналогично
сортировке слиянием, используется число
блоков, равное числу элементов массива.
В другом – можно найти пивот и тогда метод
будет аналогичен методу быстрой
сортировки.
Крючков А.В.
32

33.

Вопрос 1.7. Блочная сортировка. Реализация
На первом шаге (первый проход исходного массива)
выявляются наименьший и наибольший по значению
элементы массива.
На втором шаге для них выбираются блоки, в которые
будут заносится значения. Наиболее простой способ
деления – деление на равные части. Так для массива из 20
элементов, в котором есть натуральные числа от 10 до 99,
можно выбрать 3 блока: от 10 до 40, от 41 до 69, от 70 до
99. Реализовывать данные блоки в программах следует в
виде динамических массивов, длина которых будет
меняться по мере записи в них значений из исходного
массива. Анализ разделения по блокам будет выполняться
условными операторами.
Крючков А.В.
33

34.

Вопрос 1.7. Блочная сортировка. Реализация
На последующих шагах алгоритма внутри блоков происходят те
же действия, которые были описаны в первых его двух шагах:
выявляются максимальны и минимальный элементы и исходя
из их значений формируются блоки (промежуточные данные
программы в виде динамических массивов), в которые будут
попадать значения из дополнительных массивов, созданных на
предыдущих шагах алгоритма. Действия в процессе
повторяются до тех пор, пока размер вспомогательных массивов
превышает 1.
На заключительном шаге данные из всех вспомогательных
динамических массивов переносятся в исходный в порядке
возрастания: сначала из минимальных блоков, затем из
средних, потом из наибольших.
Крючков А.В.
34

35.

Вопрос 1.7. Блочная сортировка. Оценка
Во всех случаях в методе будет
выполнено n2 сравнений.
Крючков А.В.
35

36.

Вопрос 1.8. Голубиная сортировка
Аналогична методу сортировки подсчётом. Но в отличие
от него в данном методе мы не сразу заводим счётчики
для всех возможных значений, которые не встретятся в
исходном массиве, а используем только те, которые
актуальны для исходного массива.
Для этого нужны либо двусвязный список, позволяющий
динамически добавлять элементы, либо динамически
формируемый массив, в котором элементы «сдвигаются»
в случае необходимости.
Иногда этот метод называют сортировкой Дирихле.
Крючков А.В.
36

37.

Вопрос 1.8. Голубиная сортировка. Оценка
Во всех случаях в методе будет
выполнено n + k сравнений.
Крючков А.В.
37

38.

Вопрос 1.9. Сортировка LSD
LSD – это least significant digit, или
наименьшая значащая цифра.
Метод лучше использовать для
сортировки чисел, переведённых
в строковые значения.
Исходный массив приведен на рис.
Крючков А.В.
38

39.

Вопрос 1.9. Сортировка LSD. Реализация
Шаг первый. Создадим вспомогательный
двумерный массив длины 10 (от 0 до 9) и
ширины, равной размерности исходного
массива.
Шаг второй. Выполняем первый проход по исходному
массиву. Определяем имеют ли его элементы
одинаковое количество разрядов. Если нет – вставляем
перед их значениями дополнительные нули в качестве
старших разрядов.
Крючков А.В.
39

40.

Вопрос 1.9. Сортировка LSD. Реализация
Шаг третий. Выполняем второй проход по исходному
массиву. Определяем цифру последнего разряда
элемента исходного массива и записываем его в
элемент вспомогательного массива с первым индексом,
равным данному номеру (если последний разряд равен
2, то в элемент 2:0, если 8 – то в 8:0 при нумерации
элементов с 0).
Если элементов с такими значениями больше одного – записываем
во вспомогательный массив рядом с первым второе значение (рис.).
Последний разряд равный 1 записан в элементы 1:0 и 1:1, а равный
3, в элементы 3:0 и 3:1.
Шаг четвёртый. Выполняем проход по вспомогательному массиву в
порядке: проход по длине (категории чисел), проход по строке.
Копируем значения, полученные на 3 шаге, в исходный массив.
Крючков А.В.
40

41.

Вопрос 1.9. Сортировка LSD. Реализация
Шаг пятый. Выполняем третий проход по
исходному массиву. Определяем цифру второго
с конца разряда элемента исходного массива
и записываем его в элемент вспомогательного массива с
первым индексом, равным данному номеру (если этот
разряд равен 2, то в элемент 2:0, если 8 – то в 8:0 при
нумерации элементов с 0).
Шаг шестой. Выполняем проход по вспомогательному
массиву в порядке: проход по длине (категории чисел),
проход по строке. Копируем значения, полученные на 5
шаге, в исходный массив.
Крючков А.В.
41

42.

Вопрос 1.9. Сортировка LSD. Реализация
Шаг седьмой. Выполняем четвёртый проход по исходному массиву.
Определяем цифру третьего с конца разряда элемента исходного
массива и записываем его в элемент вспомогательного массива с
первым индексом, равным данному номеру.
Шаг восьмой. Выполняем проход по вспомогательному массиву и
копируем значения, полученные на 7 шаге, в исходный массив.
Результат на рис.
В случае, если разрядов будет больше, то и шагов будет больше.
Крючков А.В.
42

43.

Вопрос 1.9. Сортировка LSD. Оценка
Во всех случаях в методе будет
выполнено n сравнений.
Крючков А.В.
43

44.

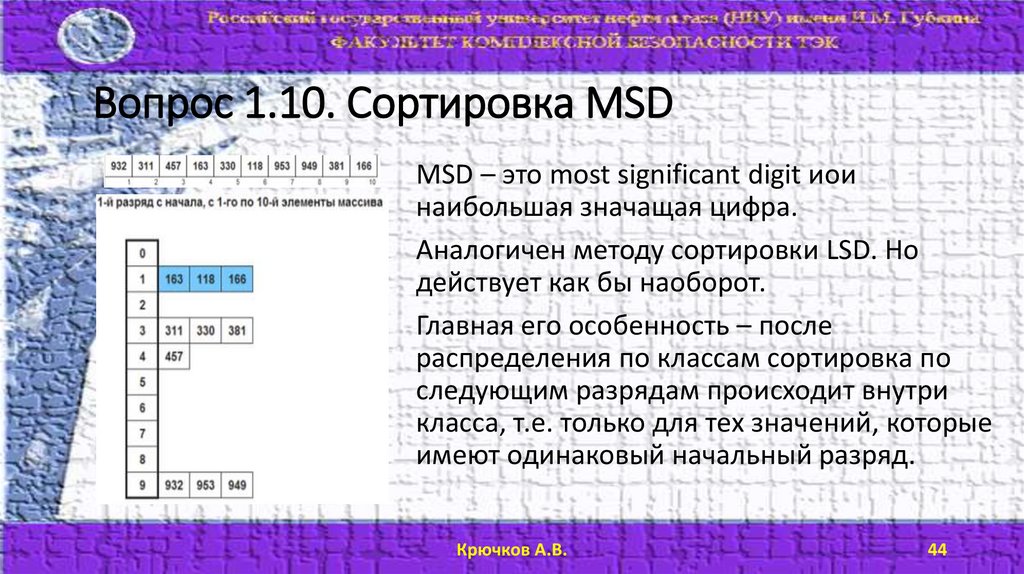
Вопрос 1.10. Сортировка MSD
MSD – это most significant digit иои
наибольшая значащая цифра.
Аналогичен методу сортировки LSD. Но
действует как бы наоборот.
Главная его особенность – после
распределения по классам сортировка по
следующим разрядам происходит внутри
класса, т.е. только для тех значений, которые
имеют одинаковый начальный разряд.
Крючков А.В.
44

45.

Вопрос 1.10. Сортировка MSD. Реализация
Шаги алгоритма метода MSD такие же, как для метода LSD. На
рисунках дано их отражение в реальном процессе (см. [6]).
Крючков А.В.
45

46.

Вопрос 1.10. Сортировка MSD. Оценка
Во всех случаях в методе будет
выполнено n сравнений.
Крючков А.В.
46

47.

Вопрос 1.11. Битонная сортировка
Этот метод сортировки выстроен на основе битонных
последовательностей и операций над ними. Это параллельный
алгоритм сортировки данных, называемый иначе, как метод
создания сортировочной сети.
Битонной (битонической) последовательностью называют такой
конечный упорядоченный набор вещественных чисел, в котором
они сначала монотонно возрастают, а затем монотонно
убывают, или набор, который приводится к такому виду путем
циклического сдвига.
Крючков А.В.
47

48.

Вопрос 1.11. Битонная сортировка
Последовательности
Последовательности, которые полностью включены в битонную, как и
последовательности, состоящие из одного или двух элементов, является
битонными.
Монотонные последовательности, для которых элементы с увеличением
номера не убывают, или, не возрастают, также считаются битонными.
Массив из одного элемента битонной последовательностью не является,
а из двух – является. Учитывая это, любое множество из двух
неотсортированных элементов можно считать битонной
последовательностью.
Битонными являются последовательности {3,5,10,4,1}, {1,5}, {10,14,5,-1,4}. Почему {4,6,1,9,2} таковой не является?
Крючков А.В.
48

49.

Вопрос 1.11. Битонная сортировка. Реализация
Шаг первый. Перед тем, как сделать первый проход
исходного массива определяем число элементов в
нём. Если он содержит один или два элемента, работа
программы завершается. Далее на первом проходе
ищем минимальный (Nmin) и максимальный (Nmax)
элементы массива, выполняя сравнение и запоминая
их номера (ключи или индексы).
Шаг второй. Создаём два вспомогательных массива,
разделив исходный массив на две примерно равные
части (вспоминаем пивот). Размер каждого из
вспомогательных массивов равен примерно
половине исходного.
Крючков А.В.
49

50.

Вопрос 1.11. Битонная сортировка. Реализация
Шаг третий. Выбираем точку «отсечения»: Nотс = (Nmax
- Nmin) / 2. Выполняем второй проход исходного
массива. Сравнивая со значением точки отсечения его
элементы, помещаем в первый вспомогательный
массив те элементы исходного, которые меньше
(Nотс), а во второй те, которые больше.
Шаг четвёртый. Выполняем шаги 1-3 для всех
вспомогательных массивов как для исходного.
Остановкой этой части алгоритма будет размер
вспомогательных массивов. Процесс остановится,
когда в них будет 2 элемента.
В отдельных случаях может появится массив с одним
элементом. Этот элемент следует присоединить к
одному из «ближайших» вспомогательных массивов.
Крючков А.В.
50

51.

Вопрос 1.11. Битонная сортировка. Реализация
В завершении алгоритма значения элементов
вспомогательных массивов, полученных на
последней итерации перед остановкой,
последовательно переписываются в исходный
массив.
На рис. показан вариант действий по ходу
сортировки в процессе работы программы,
реализующей данный метод. В показанном
варианте массив содержит число элементов,
кратное 3-й степени числа 2. Поэтому на рис.
показано 3 итерации работы со
вспомогательными массивами.
Крючков А.В.
51

52.

Вопрос 1.11. Битонная сортировка. Оценка
Во всех случаях в методе будет
выполнено n + k сравнений.
Крючков А.В.
52

53.

Вопрос 1.12. Сортировка Timsort
Метод сортировки Timsort поддерживает
гибридный алгоритм, соединяющий
сортировку вставками и слиянием.
Изобретен был в 2002 году Тимом Петерсом
(в честь него и назван). С тех пор он уже
стал стандартным алгоритмом сортировки в
Python, OpenJDK 7 и Android JDK 1.5.
Обычно состоит из двух шагов: разбиения на подмассивы и слияние.
Крючков А.В.
53

54.

Вопрос 1.12. Сортировка Timsort. Реализация
Принципы работы алгоритма:
- исходный массив делится на
подмассивы;
- подмассивы сортируются вставками;
- сортировкой слиянием подмассивы
попарно объединяются до тех пор,
пока не останется всего 2 из них;
Крючков А.В.
54

55.

Вопрос 1.12. Сортировка Timsort. Реализация
- отсортированные элементы последних
двух подмассивов записываются в
исходный массив, используя сортировку
слиянием.
Если общее число элементов в исходном
массиве меньше 64, выполняется только
сортировка вставками.
Крючков А.В.
55

56.

Вопрос 1.12. Сортировка Timsort. Оценка
В лучшем случае будет
выполнено n сравнений.
В среднем и худшем случаях
n* log2(n) сравнений.
Крючков А.В.
56

57.

Вопрос 2. Оценка методов сортировки
Частично оценки методам сортировки уже были даны в виде
числа сравнений и перемещений элементов.
Условия выполнения оценок.
Железо и система. Процессор: Intel Core i7-3770 CPU 3.40 GHz,
ОЗУ: 8 ГБ
Тестирование проводилось на почти чистой системе Windows 10
x64, установленной за несколько дней до запуска.
Использованная IDE – Microsoft Visual Studio 2015.
Крючков А.В.
57

58.

Вопрос 2. Оценка методов сортировки. Тесты
Все тесты поделены на четыре группы.
Первая группа – массив случайных чисел по разным модулям (10,
1000, 105, 107 и 109).
Вторая группа – массив, разбивающийся на несколько
отсортированных подмассивов. Фактически брался массив
случайных чисел по модулю 109, а далее отсортировывались
подмассивы: последовательность констант – 10, 100, 1000 и т.д.
Третья группа – изначально отсортированный массив случайных
чисел с некоторым числом «свопов» — перестановок двух
случайных элементов.
Крючков А.В.
58

59.

Вопрос 2. Оценка методов сортировки. Тесты
Четвёртая группа состоит из нескольких тестов с полностью
отсортированным массивом (в прямом и обратном порядке),
нескольких тестов с исходным массивом натуральных чисел от 1
до n, в котором несколько чисел заменены на случайное, и тестов
с большим количеством повторений одного элемента (10%, 25%,
50%, 75% и 90%).
Тесты позволяют посмотреть, как сортировки работают на
случайных и частично отсортированных массивах.
Крючков А.В.
59

60.

Вопросы для закрепления материала
1. С чем связано улучшение алгоритма гномьей сортировки?
2. Опишите правила построения двоичного дерева в алгоритме
пирамидальной сортировки.
3. Что такое просеивание?
4. Что такое пивот?
5. В каком случае алгоритм быстрой сортировки называют
рандомизированным?
6. Какой первый шаг алгоритма сортировки слиянием?
7. Сколько магнитных лент применялось в «Естественном неймановском
слиянии»?
8. Каково количество сравнений в методе сортировки слиянием?
9. На чём основан алгоритм сортировки подсчётом?
Крючков А.В.
60

61.

Вопросы для закрепления материала
10. Назовите основное отличие голубиной сортировки от сортировки
подсчётом.
11. Что такое LSD?
12. Что такое МSD?
13. Что такое битонная последовательность?
14. В каком случае процесс битонной сортировки остановится?
15. При каком минимальном размере массива метод сортировки Timsort
заменяется методом сортировки вставками?
16. Комбинацией каких методов сортировки является метод сортировки
Timsort?
17. Каковы значения числа проходов для метода сортировки Timsort в
лучшем, среднем и худшем случаях?
Крючков А.В.
61

62.

Литература
1. Кнут Д., Искусство программирования, том.3, Сортировка и поиск: Пер. с
англ. – М. ООО «И.Д. Вильямс», 2018. — 832 с.
2. Глупая сортировка и некоторые другие, поумнее: электронный ресурс –
Режим доступа: https://habr.com/ru/articles/204968/. мультики (28.06.2023)
3. Описание алгоритмов сортировки и сравнение их производительности:
электронный ресурс – Режим доступа: https://habr.com/ru/articles/335920/.
(28.06.2023).
4. Методы сортировки: электронный ресурс, режим доступа –
https://habr.com/ru/articles/415935. мультики (28.06.2023)
5. Сортировки слиянием: электронный ресурс, режим доступа –
https://habr.com/ru/companies/edison/articles/431964/. мультики (28.06.2023)
6. Сортировки распределением: электронный ресурс, режим доступа –
https://habr.com/ru/companies/edison/articles/472466/. мультики (28.06.2023)
7. Алгоритм сортировки Timsort: электронный ресурс, режим доступа –
https://habr.com/ru/companies/infopulse/articles/133303/. (28.06.2023)
.
Крючков А.В.
62