Similar presentations:
Алгоритм сортировки TimSort
1. Алгоритм сортировки TimSort
Работу выполнил:Ивлев Илья 11103
2. Timsort – гибридный алгоритм сортировки основанный на Insertion Sort и Merge Sort. Timsort сначала анализирует список, который
Что такоеTimSort?
Timsort – гибридный алгоритм сортировки
основанный на Insertion Sort и Merge Sort.
Timsort сначала анализирует список, который он
пытается отсортировать, и на его основе выбирает
наилучший подход. С момента его появления он
используется в качестве алгоритма сортировки по
умолчанию в Python, Java, платформе Android и
GNU Octave.
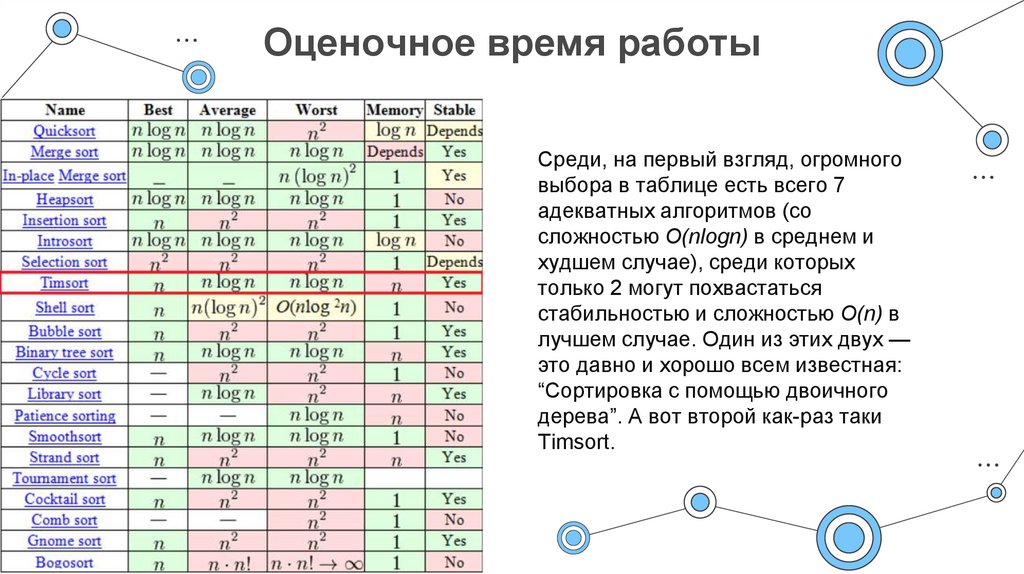
3. Оценочное время работы
Среди, на первый взгляд, огромноговыбора в таблице есть всего 7
адекватных алгоритмов (со
сложностью O(nlogn) в среднем и
худшем случае), среди которых
только 2 могут похвастаться
стабильностью и сложностью O(n) в
лучшем случае. Один из этих двух —
это давно и хорошо всем известная:
“Сортировка с помощью двоичного
дерева”. А вот второй как-раз таки
Timsort.
4. Основные понятия
N — размер входного массива
run — упорядоченный
подмассив во входном
массиве. Причём
упорядоченный либо нестрого
по возрастанию, либо строго
по убыванию. Т.е или «a0 <=
a1 <= a2 <= ...», либо «a0 > a1
> a2 > ...»
minrun — как было сказано
выше, на первом шаге
алгоритма входной массив
будет поделен на подмассивы.
minrun — это минимальный
размер такого подмассива.
Это число рассчитывается по
определённой логике из
Основные
понятия
5. Как работает данный алгоритм?
Начнем с того, что алгоритм состоитиз трех частей:
Вычисление minr
un.
Входной массив
разделяется на
подмассивы
фиксированной длины,
вычисляемой
определённым образом.
Разбиение на
подмассивы и их
сортировка.
Каждый подмассив
сортируется сортировкой
вставками, пузырьком или
любой другой устойчивой
сортировкой.
Слияние.
Отсортированные
подмассивы объединяются в
один массив с помощью
модифицированной
сортировкой слиянием.
6. Вычисление minrun
Число minrun определяется наоснове N исходя из следующих
принципов:
Вычисление
minrun
1.
Оно не должно быть слишком
большим, поскольку к подмассиву
размера minrun будет в дальнейшем
применена сортировка вставками, а
она эффективна только на небольших
массивах
2.
Оно не должно быть слишком
маленьким, поскольку чем меньше
подмассив — тем больше итераций
слияния подмассивов придётся
выполнить на последнем шаге
алгоритма.
3.
Хорошо бы, чтобы N \ minrun было
степенью числа 2 (или близким к нему).
Это требование обусловлено тем, что
алгоритм слияния подмассивов
наиболее эффективно работает на
подмассивах примерно равного
размера.
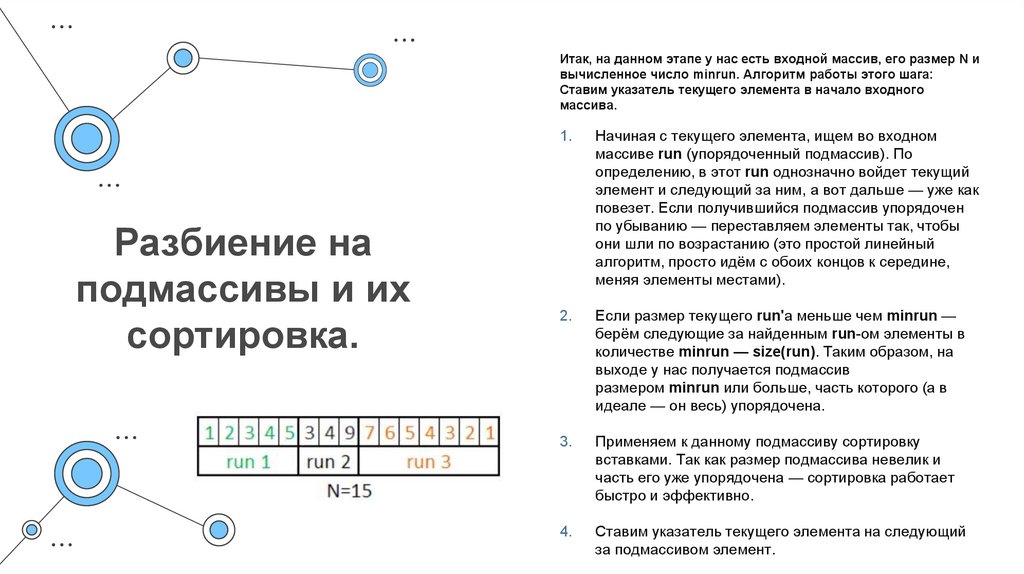
7. Разбиение на подмассивы и их сортировка.
Итак, на данном этапе у нас есть входной массив, его размер N ивычисленное число minrun. Алгоритм работы этого шага:
Ставим указатель текущего элемента в начало входного
массива.
Разбиение на
подмассивы и их
сортировка.
1.
Начиная с текущего элемента, ищем во входном
массиве run (упорядоченный подмассив). По
определению, в этот run однозначно войдет текущий
элемент и следующий за ним, а вот дальше — уже как
повезет. Если получившийся подмассив упорядочен
по убыванию — переставляем элементы так, чтобы
они шли по возрастанию (это простой линейный
алгоритм, просто идём с обоих концов к середине,
меняя элементы местами).
2.
Если размер текущего run'а меньше чем minrun —
берём следующие за найденным run-ом элементы в
количестве minrun — size(run). Таким образом, на
выходе у нас получается подмассив
размером minrun или больше, часть которого (а в
идеале — он весь) упорядочена.
3.
Применяем к данному подмассиву сортировку
вставками. Так как размер подмассива невелик и
часть его уже упорядочена — сортировка работает
быстро и эффективно.
4.
Ставим указатель текущего элемента на следующий
за подмассивом элемент.
8. Слияние.
Нужно объединить полученные подмассивы для получениярезультирующего упорядоченного массива. Для достижения
эффективности, нужно объединять подмассивы примерно
равного размера и cохранять стабильность алгоритма.
Слияние.
Описание процедуры слияния:
Шаг 0. Создается временный массив в размере меньшего из сливаемых
подмассивов.
Шаг 1. Меньший из подмассивов копируется во временный массив, но
надо учесть, что если меньший подмассив — правый, то ответ
(результат сливания) формируется справа налево. Дабы избежать
данной путаницы, лучше копировать всегда левый подмассив во
временный. На скорости это практически не отразится.
Шаг 2. Ставятся указатели текущей позиции на первые элементы
большего и временного массива.
Шаг 3. На каждом шаге рассматривается значение текущих элементов в
большем и временном массивах, берется меньший из них, копируется в
новый отсортированный массив. Указатель текущего элемента
перемещается в массиве, из которого был взят элемент.
Шаг 4. Предыдущий пункт повторяется, пока один из массивов не
закончится.
Шаг 5.Все элементы оставшегося массива добавляются в конец
9. Модификация слияния.
Модификация слияния.
Вышеуказанная процедура для них сработает, но каждый раз на
её четвёртом пункте нужно будет выполнить одно сравнение и
одно копирование. В итоге 10000 сравнений
и 10000 копирований. Timsort предлагает в этом месте
модификацию, которая получила называет галоп. Алгоритм
следующий:
Шаг 0. Начинается процедура слияния.
Шаг 1. На каждой операции копирования элемента
из временного или большего подмассива в
результирующий запоминается, из какого именно
подмассива был элемент.
Шаг 2. Если уже некоторое количество элементов
(например, в JDK 7 это число равно 7) было взято из
одного и того же массива — предполагается, что и
дальше придётся брать данные из него. Чтобы
подтвердить эту идею, алгоритм переходит в
режим галопа, то есть перемещается по массивупретенденту на поставку следующей большой
порции данных бинарным поиском (массив
упорядочен) текущего элемента из второго
соединяемого массива.
Шаг 3. В момент, когда данные из текущего массивапоставщика больше не подходят (или был достигнут
конец массива), данные копируются целиком.
10. Тестирование на сгенерированных входных данных
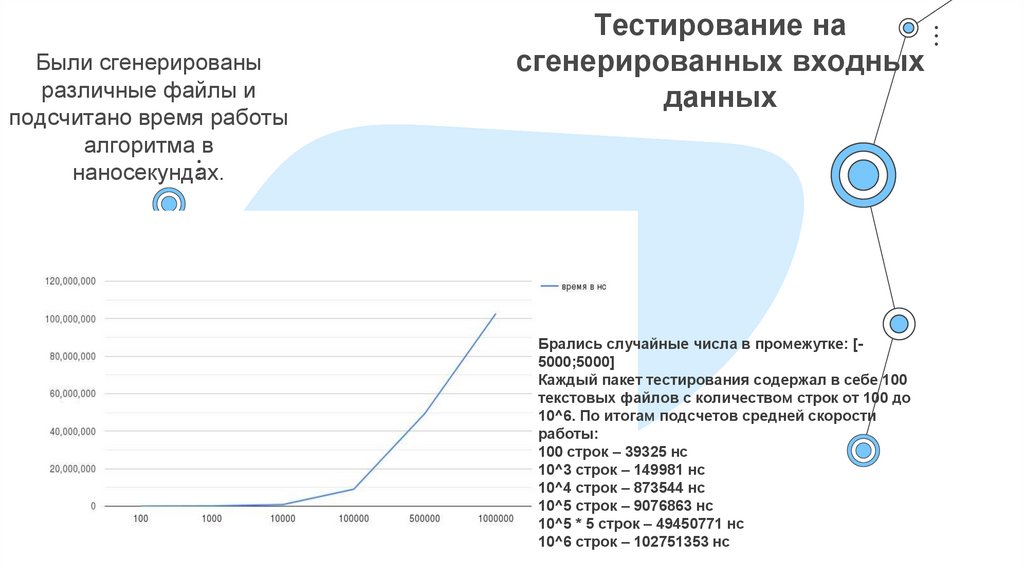
Были сгенерированыразличные файлы и
подсчитано время работы
алгоритма в
наносекундах.
Тестирование на
сгенерированных входных
данных
Брались случайные числа в промежутке: [5000;5000]
Каждый пакет тестирования содержал в себе 100
текстовых файлов с количеством строк от 100 до
10^6. По итогам подсчетов средней скорости
работы:
100 строк – 39325 нс
10^3 строк – 149981 нс
10^4 строк – 873544 нс
10^5 строк – 9076863 нс
10^5 * 5 строк – 49450771 нс
10^6 строк – 102751353 нс
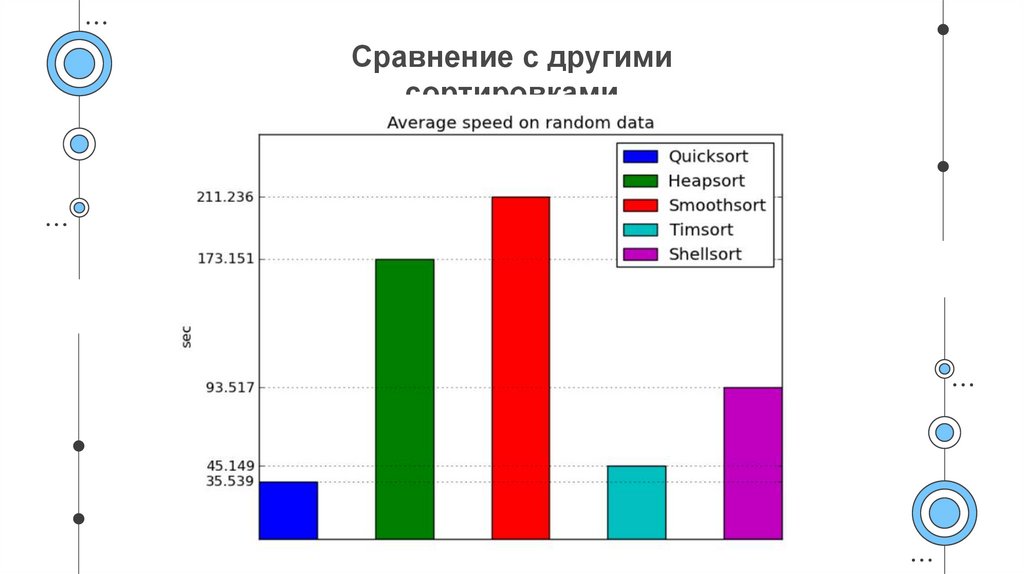
11. Сравнение с другими сортировками
12. Заключение
Данный алгоритм относительно новый, идействительно неплохо себя показывает в любых
условиях, сравнительно с другими сортировками.






 programming
programming








