Алгоритмы и программы. Тестирование. Аналитическая верификация

1. ОСНОВЫ ПРОГРАММИРОВАНИЯ

Лекция 1
Алгоритмы и программы. Тестирование.
Аналитическая верификация
1

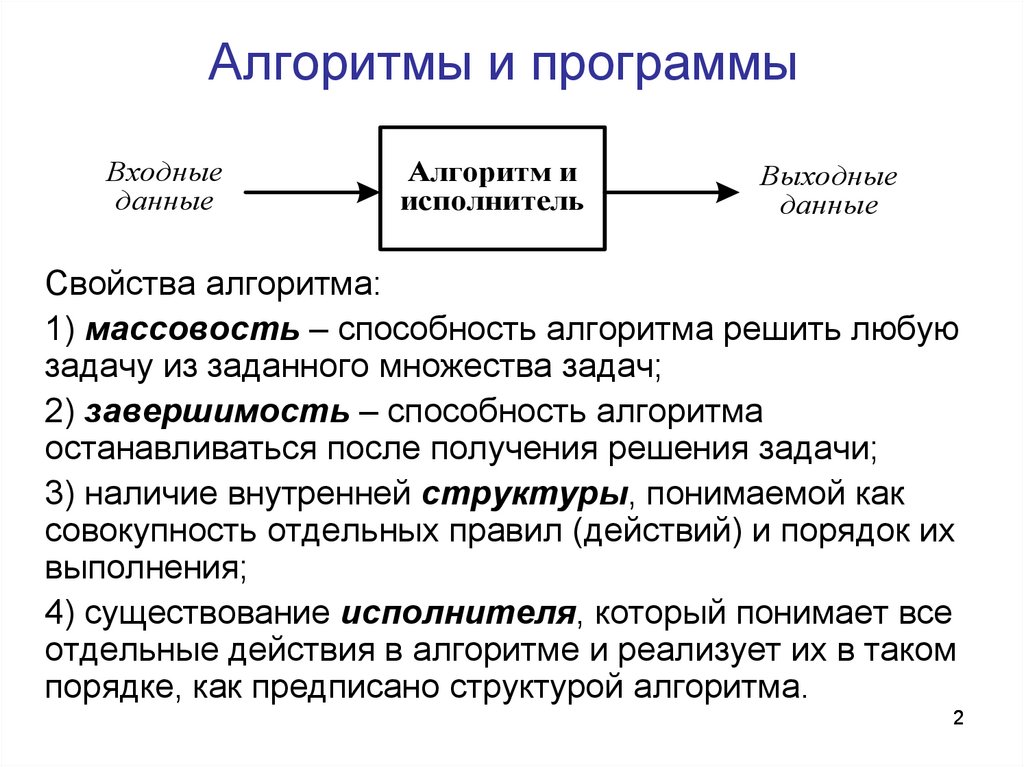
2. Алгоритмы и программы

Входные
данные
Алгоритм и
исполнитель
Выходные
данные
Свойства алгоритма:
1) массовость – способность алгоритма решить любую
задачу из заданного множества задач;
2) завершимость – способность алгоритма
останавливаться после получения решения задачи;
3) наличие внутренней структуры, понимаемой как
совокупность отдельных правил (действий) и порядок их
выполнения;
4) существование исполнителя, который понимает все
отдельные действия в алгоритме и реализует их в таком
порядке, как предписано структурой алгоритма.
2

3.

Если исполнитель алгоритма – человек, то
алгоритм может быть задан не очень строго и
полно: человек может домыслить то, чего
недостает в его описании.
Если исполнитель алгоритма – компьютер, то
алгоритм должен быть определен абсолютно
точно на строгом языке.
Программа – алгоритм, записанный на какомлибо языке программирования, например, на
языке Паскаль.
Компьютер понимает только язык машинных
команд, однако на нем очень трудно писать
программы.
3

4. Трансляция программы

Транслятор (компилятор) – это такая
программа, на вход которой подается текст
алгоритма на языке программирования –
исходный модуль, а на выходе (после
трансляции) получается программа на
машинном языке – исполняемый модуль.
Транслятор действует по строго формальным
правилам: если транслируемая программа
содержит хотя бы одну формальную
(синтаксическую) ошибку, то трансляция не
может завершиться!
После исправления всех синтаксических
ошибок транслятор создает исполняемый
модуль
4

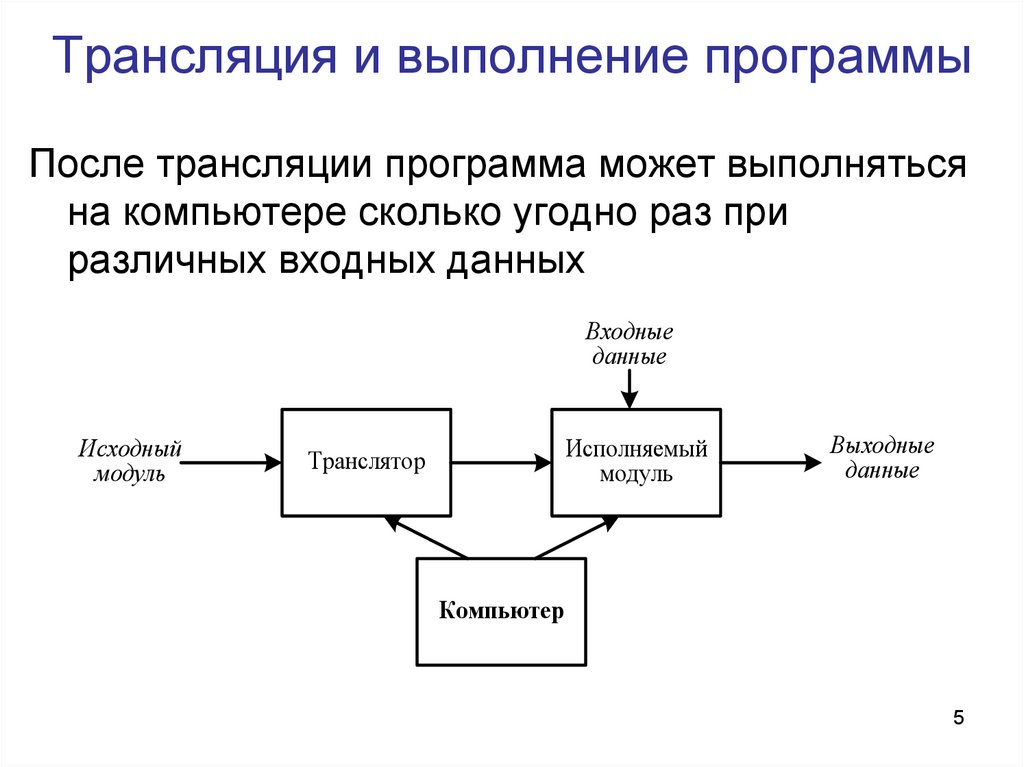
5. Трансляция и выполнение программы

После трансляции программа может выполняться
на компьютере сколько угодно раз при
различных входных данных
Входные
данные
Исходный
модуль
Исполняемый
модуль
Транслятор
Выходные
данные
Компьютер
5

6. Тестирование программы

После успешной трансляции в программе могут
остаться смысловые (семантические) ошибки.
Для их обнаружения программу необходимо
тестировать:
т.е. подготовить некоторые входные данные, подать
их на вход при выполнении программы, и сравнить
получившиеся выходные данные с ожидаемыми
выходными данными.
Чтобы выявить все возможные ошибки, тестировать
необходимо на большом количестве различных
входных данных!
Цель тестирования: выявить как можно
больше возможных ошибок!
6

7. Примеры на языке Паскаль

program ex1;
{имя программы
}
var a,b,c: integer;{описание переменных}
begin
{начало программы
}
read(a,b);
{ввод переменных a,b}
c := a + b;
{сложение a,b и
}
{ присваивание c
}
writeln(’c=’,c);
{вывод надписи и
}
{вывод результата
}
end.
{конец программы
}
Пример ввода: 39 -14
вывод: с=25
7

8. Программа вычисления корней квадратного уравнения a∙x2+b∙x+c=0

program ex2;
{имя программы
}
var a,b,c,d,x1,x2: real;{описание переменных}
begin
{начало программы
}
read(a,b,c);
{ввод переменных a,b,c
}
d := b*b – 4*a*c; {вычисление дискриминанта }
x1 := (-b – sqrt(d))/(2*a); {вычисление
}
x2 := (-b + sqrt(d))/(2*a); { корней
}
writeln(’x1=’,x1:7:3,’ x2=’,x2:7:3);
{вывод надписей и вывод результата }
end.
{конец программы
}
Пример ввода: 1 -3.5 -1
вывод: x1= -0.500 x2=
4.000
8

9. Исчерпывающее тестирование программы

Тест: экземпляр входных данных p и ожидаемые
выходные данные q, необходимые для проверки
правильности результата вычислений
Пример: программа сложения двух целых чисел
(тип – integer), диапазон каждого из чисел
от –2147483648 до +2147483647, всего их 232.
Количество всех возможных тестов, т.е.
различных пар слагаемых, 264 = 18446744073709551616.
При 109 (миллиард) проверках в секунду для исчерпывающего тестирования потребуется более 500 лет!
Закон Э. Дейкстры: «Тестированием можно доказать
наличие ошибок в программе, но никогда – их
отсутствие».
9

10. Методы тестирования программы

Тестирование методом черного ящика: при
создании тестов внутренняя структура
программы не принимается во внимание.
Тестирование методом белого ящика: тесты
создаются на основе внутренней структуры
программы, так, чтобы все компоненты
программы выполнялись в разных тестах.
Пошаговое тестирование: выполнение
программы в интерактивном режиме с
отслеживанием промежуточных значений
переменных. Возможно для тестов, когда
количество шагов не слишком большое.
10

11. Аналитическая верификация программ

(Доказательство правильности программ)
Предусловие – логическое условие для входных данных.
Постусловие – логическое условие для выходных данных.
1) доказательство завершимости;
2) доказательство истинности постусловия после
завершения программы.
Теорема. Любой алгоритм можно записать, используя
только следующие действия (операторы):
- присваивание, арифметические операции,
- последовательность действий,
- ветвление (конструкция if – then – else),
- цикл (конструкция while – do).
11

12.

Присваивание. Если имеется некоторое логическое
условие P(x), в запись которого входит
переменная x, то для присваивания
x:=w
предусловие: P(w), постусловие: P(x).
Сокращенно: {P(w)} x:=w {P(x)}
Здесь х – переменная, w – формула, в ней
арифметические операции и функции
применяются к переменным и константам.
После выполнения всех действий в формуле w
результат вычислений присваивается
переменной х.
12

13.

Формула записывается подряд, в строку.
Переменные и константы в формуле: целые или
вещественные (приближенные).
Переменная – последовательность букв и (или)
цифр, начинается всегда с буквы.
Операции: +, –, * (умножение), / (вещественное
деление), div (деление для целых), mod (остаток
от деления для целых).
Функции: sqrt (квадратный корень), abs
(абсолютное значение ), sin (синус), cos
(косинус), exp (экспонента) и др.
Порядок вычислений: слева-направо, но вначале
операции *, /, div, mod, а затем + и – .
Круглые скобки изменяют порядок вычислений.
13

14.

Последовательность операторов (действий)
A
B
Если А и В – операторы, для которых
выполняются пред- и постусловия:
{P} А {Q} и {Q} В {R},
То:
{P} А; В {R}
постусловие для А есть предусловие для В
Последовательность операторов, взятая в
«скобки» begin и end, – это единый оператор.
14

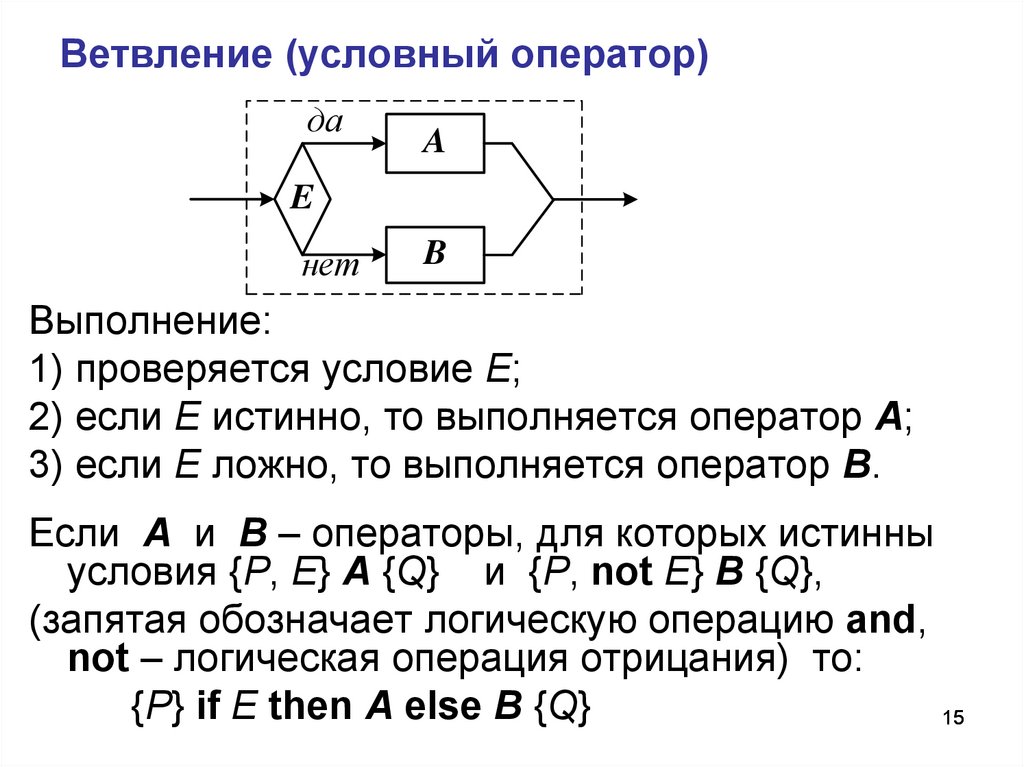
15. Ветвление (условный оператор)

да
A
E
нет
B
Выполнение:
1) проверяется условие Е;
2) если Е истинно, то выполняется оператор А;
3) если Е ложно, то выполняется оператор В.
Если А и В – операторы, для которых истинны
условия {P, Е} А {Q} и {P, not Е} В {Q},
(запятая обозначает логическую операцию and,
not – логическая операция отрицания) то:
{P} if E then A else B {Q}
15

16.

Цикл (с условием)
да
E
A
нет
Выполнение:
1) проверяется условие Е;
2) если Е истинно, то выполняется оператор А, после
чего переход к п.1;
3) если Е ложно, то выполнение цикла заканчивается.
Если A – оператор, для которого выполняется условие
{P, E} A { P },
то: {P} while E do A { P, not E }.
Условие P, которое не изменяется в процессе
выполнения цикла, называется инвариантом цикла.
16

17. Методы доказательства

1) последовательное перечисление
выполняемых действий;
2) перечисление вариантов,
применяется для ветвлений;
3) метод математической индукции,
применяется для циклов и рекурсивных
процедур;
4) инвариант, также применяется для
циклов и рекурсивных процедур;
5) метод эквивалентов;
6) метод абстракции.
17

18. Примеры

1. Предусловие: x=a, y=b
z:=y; y:=x; x:=z
Постусловие: x=b, y=a
Доказательство: проверка по шагам
___________________________________
2. Предусловие x=a, y=b
if x<y then
begin
z:=y; y:=x; x:=z
end
Постусловие x≥y, x=max(a,b), y=min(a,b)
Доказательство (перечисление вариантов):
1) на входе: x≥y, на выходе: x≥y
2) на входе: x<y, на выходе: x≥y
18

19. Программа вычисления корней квадратного уравнения с проверкой

program ex3;
{имя программы
}
var a,b,c,d,x1,x2: real;{описание переменных}
begin
{начало программы
}
read(a,b,c);
{ввод переменных a,b,c
}
d := b*b – 4*a*c; {вычисление дискриминанта }
if d>=0 then begin {проверка того, что d≥0
}
x1 := (-b – sqrt(d))/(2*a); {вычисление }
x2 := (-b + sqrt(d))/(2*a); { корней
}
writeln(’x1=’,x1:7:3,’ x2=’,x2:7:3);
end
else writeln(’error!’); {если d<0 то ошибка }
end.
{конец программы
}
19

20.

Доказательство для оператора if
(метод - перечисление вариантов):
1. d>=0 вычисляются и выводятся x1,x2
2. d<0 выводится error!
Пример теста 1.
Ввод: 1 -2 3
вывод: error!
Пример теста 2.
Ввод: 2 -10 12
вывод: x1= 2.000
x2=
3.000
20

21. Метод математической индукции

1) базис, 2) предположение, 3) индуктивный вывод.
На этапе базиса проверяют, что доказываемое
утверждение P(n) относительно параметра
индукции n справедливо при n = n0.
На втором этапе делается предположение, что
утверждение P(n) справедливо для всех
значений n, не бóльших, чем некоторое k,
k ≥ n ≥ n 0.
На этапе индуктивного вывода доказывается, что
P(n) будет справедливо при n = k + 1 > n0. Из
этого следует, что утверждение P(n)
справедливо для любого n ≥ n0.
21

22. Пример математической индукции Sn = 12 + 22 + … + n2 , ≈ n3 / 3 при n → ∞

Пример математической индукции
Sn = 12 + 22 + … + n2 ,
2n 3 3n 2 n
≈ n3 / 3 при n → ∞
Sn
6
Базис. При n = 0 сумма Sn = 0, с другой
стороны, при n = 0 формула верна.
Предположение. Пусть при n ≥ 0 формула
верна.
Индуктивный вывод. При n + 1:
3
2
2n 3 3n 2 n
2
(
n
1
)
3
(
n
1
)
(n 1)
2
S n 1
(n 1)
6
6
22

23.

Предусловие: n≥1.
f:=1; i:=2;
while i<=n do
begin f:=f*i;
i:=i+1
end
Постусловие: f=1*2*...*n, i=n+1.
Базис. Если n=1, то f=1,i=2 .
Предположение: при n=k, n≥1 постусловие
f=1*2*...*k, i=k+1.
Индуктивный вывод: дополнительный шаг цикла
при i=k+1 : f=(1*2*...*k)*(k+1), i=k+2.
Т.е. постусловие справедливо при n=k+1.
23

24. Инвариант

Инвариант – такое логическое условие,
которое истинно как до выполнения
алгоритма, так и после его завершения.
Доказательство для цикла:
1. Доказать завершимость цикла.
2. Проверить что условие истинно до
выполнения цикла.
3. Проверить, что условие истинно при
однократном выполнении цикла.
Тогда: согласно математической индукции
следует, что условие будет истинным
после завершения цикла.
24

25. Пример. Инвариант

предусловие: n≥1.
f:=1; i:=2;
while i<=n do
begin f:=f*i;
i:=i+1
end
постусловие: f=1*2*...*n, i=n+1.
Полное предусловие: n≥1, i=2, f=1, т.е.
справедливо: f=1*...*(i-1)
Полное постусловие: n≥1, i=n+1,
f=1*...*n,т.е. справедливо: f=1*...*(i-1).
Инвариант: f=1*...*(i-1).
25

26. Примеры тестов.

Тесты по методу черного ящика:
- минимально возможное n=0;
- на 1 больше минимально возможного n, n=1;
- значение n, несколько большее, например, n=6.
Тесты по методу белого ящика:
- такое n, чтобы цикл ни разу не выполнялся, n=1;
- такое n, чтобы цикл выполнился 1 раз, n=2;
- значение n, несколько большее, например, n=6.
Т.е. все тесты: n=0, n=1, n=2, n=5
На выходе соответственно: f=1, f=1, f=2, f=120
26

27. Метод эквивалентов

Если две программы в процессе выполнения
изменяют все переменные из набора х1, . . . , хn
одинаковым образом, то эти две программы
эквивалентны относительно этого набора
переменных.
Тогда доказательство для одной из программ
справедливо и для другой программы.
При этом в программах могут выполняться другие
действия над другими переменными, не
входящими в набор х1, . . . , хn.
27

28. Примеры эквивалентных программ

Цикл
for i:=a to b do D;
Эквивалентен циклу
i:=a;
while i<=b do begin D; i:=i+1 end;
_____________________________________________________________________________________________________________
Предусловие для обоих циклов: i=a, a<=b+1.
После завершения цикла while: i=b+1.
После завершения цикла for по правилам языка
Паскаль значение i не определено, но в постусловии его следует считать равным b+1.
28

29. Примеры эквивалентных программ

Цикл
for i:=a downto b do D;
Эквивалентен циклу
i:=a;
while i>=b do begin D; i:=i-1 end;
_____________________________________________________________________________________________________________
Предусловие для обоих циклов: i=a, a>=b-1.
После завершения цикла while: i=b-1.
После завершения цикла for по правилам языка
Паскаль значение i не определено, но в постусловии его следует считать равным b-1.
29

30. Примеры эквивалентных программ

Если S1 и S2 – операторы, в которых используются
различные переменные, то эквивалентны
последовательности
S1; S2
и
S2; S1
_______________________________________________
Эквивалентны операторы
case i of
a1:S1;
a2:S2
else S3
end
и
if i=a1 then S1
else if i=a2 then S2
else S3
30

31. Массивы (индексируемые переменные)

Пример описания массива M с одним индексом
(одномерного), элементы массива нумеруются от 1 до
100 и имеют тип real:
var M: array[1..100]of real;
Пример описания массива M2 с двумя индексами
(двумерного), элементы массива нумеруются от 1 до
10 первым и от 0 до 49 вторым индексом и имеют тип
integer:
var M2: array[1..10,0..49]of integer;
Всего в массиве М2 – 500 элементов.
Примеры индексирования элементов массива М:
M[5], M[i], M[i+5] (i такое, чтобы индекс был в
диапазоне от 1 до 100).
Примеры индексирования элементов массива М2:
M2[5,0], M2[i,j], M2[i+5,j-1].
31

32. Программа ввода массива из 10 элементов и их вывода

program ex4;
{имя программы}
var i: integer;
{описание переменных}
M: array[1..10]of integer;
begin
{начало программы}
for i:=1 to 10 do
{ввод элементов массива М}
read(M[i]);
for i:=10 downto 1 do
{вывод элементов}
write(M[i],’ ’); {массива М в обратном порядке}
writeln;
{переход к новой строчке вывода}
end.
{конец программы}
Пример ввода: 1 3 21 4 -9 10 125 33 31 2
вывод: 2 31 33 125 10 -9 4 21 3 1
32

33. Пример. Инвариант (с учетом эквивалентов)

предусловие: i=2, min=A[1].
min:=A[1];
for i:=2 to n do
if min>A[i] then min:=A[i];
постусловие:
i=n+1, min = min{A[1],...,A[n]}.
Инвариант: min = min{A[1],...,A[i-1]}.
33

34. Примеры тестов.

Тесты по методу черного ящика:
- минимальное n=1, массив А: А[1]=10;
- n на 1 больше минимального, n=2, два варианта массива А:
1) А[1]=10, А[2]=5;
{убывание}
2) А[1]=5, А[2]=10;
{возрастание}
- n несколько большее, например, n=4, массив А, например:
1) А[1]=10, А[2]=5, А[3]=1, А[4]=-2; {убывание}
2) А[1]=-5, А[2]=0, А[3]=1, А[4]=7; {возрастание}
3) А[1]=5, А[2]=5, А[3]=5, А[4]=5;
{равенство}
Тесты по методу белого ящика:
- такое n, чтобы цикл ни разу не выполнялся, n=1;
- n=2, чтобы цикл выполнился 1 раз,
1) такой массив А, чтобы условие min>A[i] было истинным;
2) такой массив А, чтобы условие min>A[i] было ложным;
- n несколько большее, например, n=4, массив А такой, чтобы:
1) условие min>A[i] всегда было истинным;
2) условие min>A[i] всегда было ложным;
Здесь тесты по обоим методам могут быть почти одинаковыми.
34

35. Пример. Инвариант (с учетом эквивалентов)

предусловие: i=2, k=1.
min:=A[1]; k:=1;
for i:=2 to n do
if min>A[i] then
begin min:=A[i]; k:=i end;
постусловие:
i=n+1, k = argmin{A[1],...,A[n]}.
Инвариант:
k = argmin{A[1],...,A[i-1]}.
Тесты такие же, как для предыдущего алгоритма
35

36. Метод абстракции

Применяется для доказательства сложных программ:
отдельные её части – это программы со своими входами и
выходами, т.е. со своими пред- и постусловиями.
Каждая такая часть доказывается независимо (абстрагируясь)
от других частей.
Вся программа в целом доказывается абстрагируясь от её
отдельных частей в предположении их правильности.
Применяется также при разработке сложных программ (метод
поэтапной разработки, метод сверху-вниз):
- вначале создаётся общая программа (на первом уровне), в
которой операторы – это программы второго уровня;
- затем создаются программы второго уровня, в которых
операторы – это программы третьего уровня и т.д.
36

37.

Пример. Вычисление всех простых чисел от 2 до n:
for i:=2 to n do
begin j:=2; p:=0;
while (j<i)and(p=0) do
if i mod j = 0
then p:=1
else j:=j+1;
if p=0 then writeln(i)
end;
Предусловие для внешнего цикла: i=2
Постусловие: i=n+1
Инвариант: «вычислены все простые числа от 2 до i-1
Предусловие для внутреннего цикла: j=2,p=0
Постусловие: j=n,p=0,тогда число i простое ,
или: j<n,p=1,тогда число i не простое
Инвариант: «число не делится на числа от 2 до j-1
и: (число не делится на j,p=0)
или: (число делится на j,p=1)
37

38. Анализ трудоёмкости

Трудоёмкость: функция зависимости количества элементарных
действий в программе (следовательно, времени вычислений) от
размера входных данных n, при n →∞.
Чаще всего оценивают трудоёмкость в наихудшем, когда реальная
трудоёмкость не больше трудоёмкости в наихудшем. Иногда
оценивают трудоёмкость в наилучшем или в среднем.
Пример – вычисление номера элемента массива X, который
содержит наибольшее значение:
k:=1;
for i:=2 to n do
if X[k]>X[i] then k:=i;
Трудоёмкость T(n) = A·n + B. При n →∞ величиной B можно
пренебречь. Коэффициент A зависит от быстродействия
компьютера, от качества транслятора, поэтому пишут:
T(n) = O(n). Здесь O(n) – (порядок трудоёмкости) линейный.
38

39.

Пример. Вычисление суммы S элементов квадратной
матрицы D размером n x n:
S:=0;
for i:=1 to n do
for j:=1 to n do
S:=S+D[i,j];
Здесь трудоёмкость T(n) = A·n2 + B·n + C. При n →∞
величинами B и С можно пренебречь. Порядок
трудоёмкости O(n2) – квадратичный.
39

40.

Пример. Вычисление всех простых чисел от 2 до n:
for i:=2 to n do
begin j:=2; p:=0;
while (j<i)and(p=0) do
if i mod j = 0
then p:=1
else j:=j+1;
if p=0 then writeln(i)
end;
Здесь трудоёмкость в наихудшем T(n) = A·n2 + B·n + C.
Общее количество выполнений внутреннего цикла не
превышает:
1 + 2 + 3 + . . . + (n − 2) = (n − 1)· (n − 2) / 2 ≈ n2 / 2
Т.е. порядок трудоёмкости O(n2) – квадратичный.
40

41.

Пример. Ускорение программы вычисления всех
простых чисел, не превышающих n:
for i:=2 to n do
begin j:=2; p:=0; x=sqrt(i);
while (j<x)and(p=0) do
if i mod j = 0
then p:=1
else j:=j+1;
if p=0 then writeln(i)
end;
Трудоёмкость в наихудшем T(n) = A·n3/2 + B·n + C.
Общее количество выполнений внутреннего цикла не
превышает:
1 2 3 ... n n n
Т.е. порядок трудоёмкости O(n3/2).
41

42.

При сравнении двух алгоритмов (решающих одну и
ту же задачу): тот алгоритм лучше (имеет
меньшую трудоёмкость), у которого порядок
трудоёмкости меньше.
Например, O(n) – линейная трудоёмкость лучше,
чем O(n2) – квадратичная трудоёмкость.
Так, при увеличении n в 10 раз время работы
алгоритма с линейной трудоёмкостью увеличится
в 10 раз, алгоритма с трудоёмкостью O(n3/2) – в 31
раз, а алгоритма с квадратичной трудоёмкостью –
в 100 раз!
Если же у алгоритмов порядок трудоёмкости
одинаков, то лучше тот алгоритм, у которого
множитель А перед функцией меньше.
42