Similar presentations:
Рекуррентные алгоритмы. Основы программирования
1. ОСНОВЫ ПРОГРАММИРОВАНИЯ
Лекция 2Рекуррентные алгоритмы
1
2. РЕКУРРЕНТНАЯ ПОСЛЕДОВАТЕЛЬНОСТЬ
Числовая последовательность {xk}называется рекуррентной ранга p,
если
k 0, 1, ..., p 1,
xk ak ,
xk f (k , xk 1 , xk 2 ,..., xk p ), k p, p 1, ...
где a0, a1, …, ap – 1 – константы,
f – функция.
2
3.
Сумма элементов ai – рекуррентнаяпоследовательность ранга 1:
S 0 0,
Si Si 1 ai ,
i 1, 2, ..., n .
S:=0;
for i:=1 to n do
S:=S + a(i);
a(i)- некоторая формула или функция
3
4. ПРИБЛИЖЕННОЕ ВЫЧИСЛЕНИЕ ПРЕДЕЛА ПОСЛЕДОВАТЕЛЬНОСТИ
Последовательность может иметь предел приn → ∞. Пусть
S1 f1 ,
S k S k 1 f k , k 2, 3, ...
а слагаемые fk стремятся к нулю при k → ∞.
f 1 a,
f k p(k , f k 1 ), k 2, 3, ...
4
5. ВЫЧИСЛЕНИЕ ПРЕДЕЛА ПОСЛЕДОВАТЕЛЬНОСТИ
S:=a; f:=a; k:=2;while abs(f)>=eps do
begin
f:= p(k,f);
S:=S+f;
k:=k+1
end;
Инвариант: f = fk-1, S = Sk-1
Трудоёмкость программы, т.е. количество k
выполнений цикла, определяется из формулы:
fk+1 < eps,
где eps – заданная точность вычисления
последовательности.
5
6. Пример. Приближенное значение функции sin x
Пример. Приближенное значениефункции sin x
3
5
2 k 1
x
x
x
k 1
sin x x
...( 1)
3! 5!
(2k 1)!
Рекуррентное соотношение для элементов суммы
f 1 x,
2
x
f f
, k 2, 3, ...
k
k
1
(2k 1)(2k 2)
6
7.
S:=x; f:=x; k:=2;while abs(f)>=eps do
begin
f:=-f*x*x/((2*k-1)*(2*k-2));
S:=S+f;
k:=k+1
end;
количество k выполнений цикла определяется
из неравенства:
2 k 1
x
f k 1
(2k 1)!
7
8. Рекуррентная последовательность Герона
s 0 1,s 1 s a , k 1, 2, ...
k 2 k 1 s k 1
Докажем, что lim s k a при a ≥ 0.
k
Доказательство. Пусть s k a ek , где
ek – ошибка k-го приближения. Тогда
1
a
sk a ek 1
2
a ek 1
2
k 1
1
e
a
a ek
2 a ek 1
8
9.
( a 1)1
e1 s1 a 1 a a
0
2
2
2
2
e
1
k 1
ek
0,
2 a ek 1
1
ek ek 1 ,
2
k 2, ...
Т.е. e1 /e2 ≥ 2, e1/e3 ≥ 4, …, e1/ek ≥ 2k – 1,
откуда:
1 a
k log 2
2ε
9
10. Вычисление квадратного корня по формуле Герона
s:=(1+a)/2; e:=eps;while e>=eps do
begin s1:=(s+a/s)/2;
e:=s-s1; s:=s1
end;
Трудоемкость: O(log (1+a)/ɛ)
10
11. МЕТОД ДИХОТОМИИ ВЫЧИСЛЕНИЯ КОРНЯ ФУНКЦИИ
На интервале [a, b] задана непрерывнаяфункция y = f(x), значения функции на концах
интервала f(a) и f(b) имеют разные знаки.
Требуется найти такое z, что | x0 – z | ≤ ε / 2 .
Рекуррентная последовательность пар чисел
{ui , vi}:
u0 a, v0 b,
ui 1 ui , vi 1 (ui vi ) / 2, sign f (ui ) sign f ((ui vi ) / 2)
u (u v ) / 2, v v , sign f (u ) sign f ((u v ) / 2),
i
i
i 1
i
i
i
i
i 1
11
12.
u:=a; v:=b; x:=(u+v)/2;while (v-u)>=eps do
begin
if f(u)*f(x)<=0 then v:=x
else u:=x;
x:=(u+v)/2
end;
b a
Трудоемкость: k log 2
ε
12
13. Полином от x степени n в виде формулы Горнера
Pn ( x) an x n an 1x n 1 ... a1x a0(...(an x an 1 ) x ... a1 ) x a0
где an, an - 1, …, a1, a0 – коэффициенты
Вычисление полинома
P0 a n ,
Pi Pi 1 x a n i , i 1, 2, ..., n .
P:=a[n];
for i:=1 to n do
P:=P*x+a[n-i];
13
14. Вычисление цифр a0, a1, …, an неотрицательного целого числа Pn при заданном значении основания x:
Вычисление цифр a0, a1, …, an неотрицательногоцелого числа Pn при заданном значении основания x:
ai Pn i mod x,
Pn i 1 Pn i div x,
i 0, 1, ..., n, Pn i 0,
i:=0;
while P>0 do
begin
a[i]:=P mod x;
P:=P div x;
i:=i+1
end;
n:=i-1;
14
15. Числа Фибоначчи задаются рекуррентной последовательностью ранга 2
f 0 0, f 1 1,f k f k 1 f k 2 , k 2, 3, ... ,
f1:=0; f2:=1;
for k:=2 to n do
begin
f3:=f2+f1;
f1:=f2; f2:=f3
end;
15
16. Формула Муавра для чисел Фибоначчи
nn
1 5
1 1 5
fn
5 2
2
Доказательство.
Базис. При n = 0 и n = 1 проверяем простой подстановкой.
Предположение. Пусть при n ≥ 0 формула верна.
Вывод. При n + 1 получаем:
n 1
n 1
n
n
1 5
1 1 5 1 5 1 1 5
f n 1
5 2
2
5 2 2
n 1
n 1
1 5
1 1 5
5 2
2
16
17.
учитывая, чтоЧисло
2
1 5
1 5
1
2
2
lim ( f k 1 / f k ) (1 5 ) / 2 1,618
k
называют золотым сечением
17
18. Алгоритм Евклида
Вычисляет наибольший общий делитель НОД(a, b)двух целых чисел a ≥ 0, b ≥ 0, основан на
инвариантных соотношениях:
1) НОД(a, 0) = a;
2) НОД(a, b) = НОД(b, a);
3) НОД(a, b) = НОД(a mod b, b), a ≥ b > 0.
Последнее следует из: 4) НОД(a, b) = НОД(a – b, b).
Докажем 4-е. Пусть НОД(a, b) = d, НОД(a – b, b) = c.
a b a b
a b b
Тогда
, причем
,
– целые, и тогда
c
c c
c
c
a
может быть целым лишь в случае, если c = d.
c
18
19. Последовательность пар {xi, yi} такова, что:
Последовательность пар {xi, yi} такова, что:НОД(xi, yi) = НОД(a, b), max(xi, yi) > max(xi+1 , yi+1)
x 0 a, y 0 b,
xi 1 xi mod y i , y i 1 y i , при xi y i 0,
y y mod x , x x , при y x 0.
i 1
i
i
i 1
i
i
i
x:=a; y:=b;
while (x>0)and(y>0) do
if x>=y then x:=x mod y
else y:=y mod x;
if x>0 then nod:=x else nod:=y;
19
20. Трудоемкость алгоритма Евклида
Наихудший случай: если при fk ≥ max(a, b) > fk – 1 ,где fk , fk – 1 – числа Фибоначчи, выполняется условие:
max(a, b) = fk , min(a, b) = fk – 1 .
Тогда k – количество выполнений цикла. Пренебрегая
вторым слагаемым в формуле Муавра:
1 1 5
fn
5 2
n
и логарифмируя левую и правую части, получим:
k log ( 5 f k ) log 2 log 2 ( 5 f k )
k log 2 log 2 ( 5 max( a, b)) 1.4 log 2 max( a, b)
Т.е. трудоемкость имеет порядок O(log max(a, b)).
20
21.
Возведение числа x в положительнуюцелую степень p. Результат – число z.
z:=1; s:=p; y:=x;
while s>0 do
begin
if odd(s) then
begin s:=s-1; z:=z*y end;
s:=s div 2; y:=y*y
end;
Функцию odd(s)можно заменить на(s and 1)=1
Присваивание s:=s div 2;
можно заменить на s:=s shr 1;
21
22.
Предусловие цикла: z=1, s=p, y=x;постусловие: s=0.
Инвариант: z*ys = xp.
z*ys = (z*y)*ys-1 = z*(y*y)s/2
После очередного шага цикла степень s уменьшается
как минимум в 2 раза. Пусть вначале выполняется:
s = p, 2k ≤ p < 2k+1,
то после k =└log2 p┘+ 1 шагов (максимум) степень s
уменьшится до 0.
Т.е. всего шагов цикла: └log2 p┘+ 1, количество
умножений не более 2∙(└log2 p┘+ 1),
22
порядок трудоемкости O(log p).








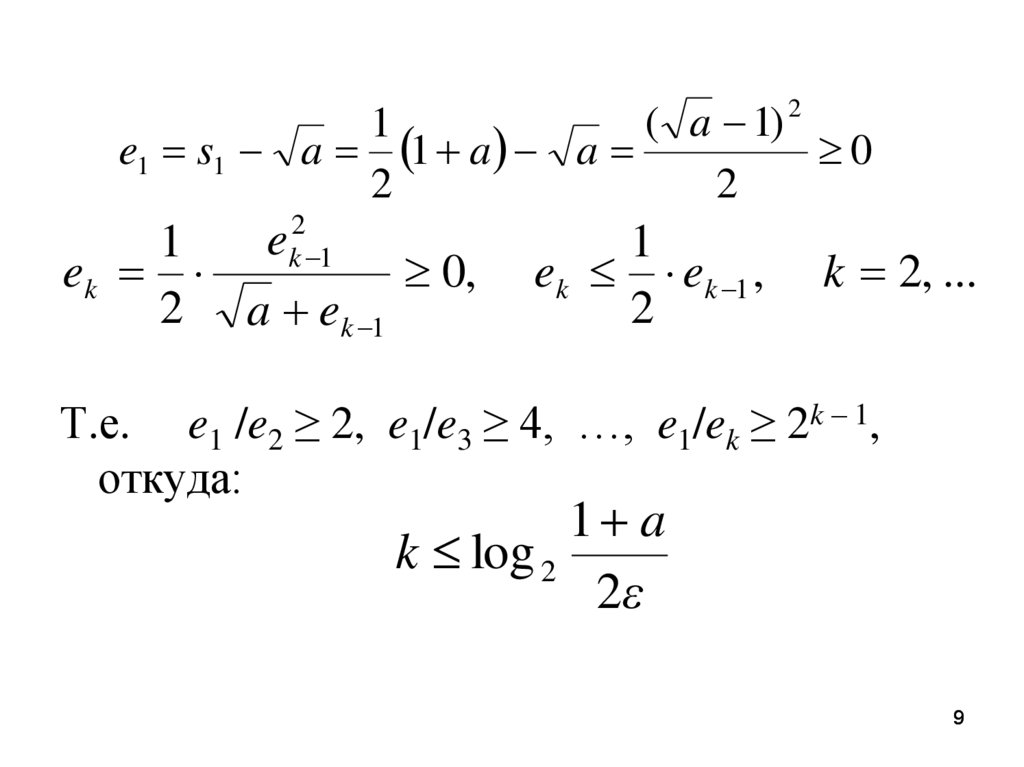













 programming
programming








