Similar presentations:
Уравнения. Корень уравнения
1. Уравнения.
Уравнение – равенство, содержащее неизвестноеобозначенное буквой, значение которого надо найти.
число,
Корень
уравнения
–
значение
неизвестного,
при
подстановке
которого уравнение обращается в верное числовое равенство.
Решить уравнение – найти все его корни или установить, что их нет.
2. Типы уравнений
3. Линейные уравнения
4. Уравнения, сводящиеся к линейным
5. Уравнения, сводящиеся к линейным
6. Уравнения, сводящиеся к линейным
7. Неполные квадратные уравнения
8. Неполные квадратные уравнения
9.
10. Полные квадратные уравнения
11. Полные квадратные уравнения
12. Неравенства
13. Неравенства
14. Системы неравенств
15. Системы неравенств
16. Квадратные неравенства
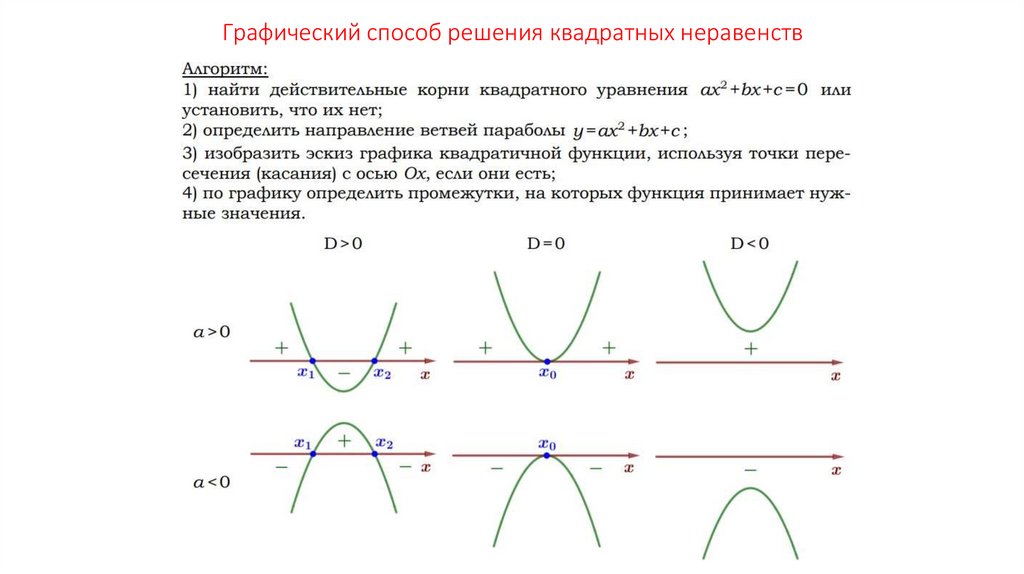
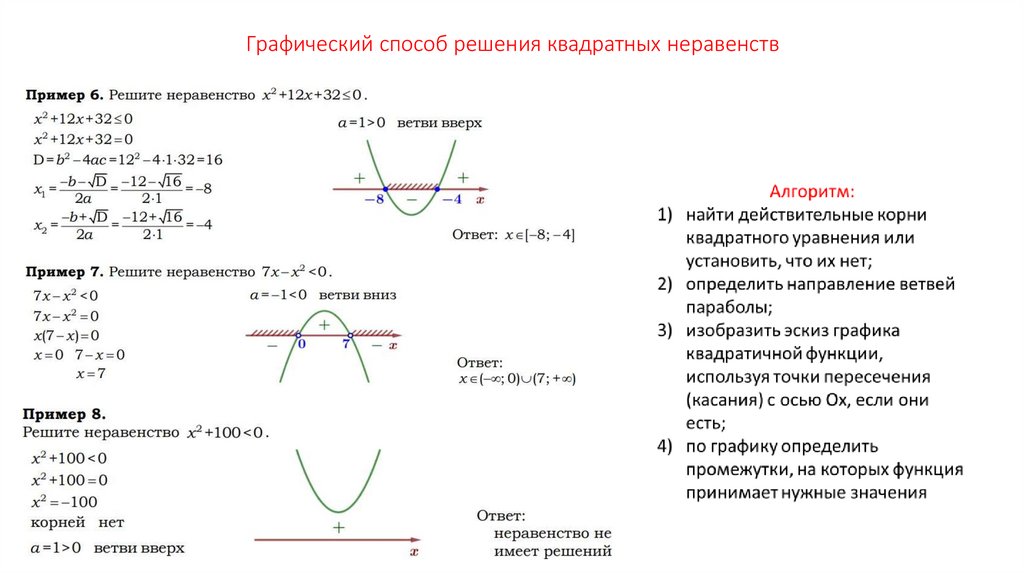
17. Графический способ решения квадратных неравенств
18. Графический способ решения квадратных неравенств
19. Метод интервалов
20. Метод интервалов
1) найти нули функции,решив квадратное
уравнение;
2) отметить положение
нулей на оси Ox;
3) определить знаки
функции в промежутках
между нулями;
A. вычислить значение
функции в точке x =0 (или,
например, x =1 ), отметить
знак в соответствующем
промежутке,
B. определить знаки в
остальных промежутках
по правилу
21. Метод интервалов
22. Рациональные уравнения
Рациональное уравнение – это такое уравнение, в обеих частях которого содержатсярациональные выражения.
Рациональное уравнение будет являться целым в том случае, если в записи левой и
правой его частей содержатся целые рациональные выражения.
Рациональное уравнение будет являться дробным в том случае, если одна или обе
его части содержат дробь.
23. Дробно-рациональные уравнения Уравнение вида называется дробно-рациональным. Его решение сводится к решению системы
Дробно-рациональные уравненияУравнение виданазывается дробнорациональным. Его решение сводится к
решению системы
24. Иррациональные уравнения Иррациональное уравнение имеет вид:
25.
26. Иррациональные уравнения
27. Рациональные неравенства
28.
3. Решите неравенство:29.
Полезные материалы, ресурсы:• Материалы курса «Система подготовки к ЕГЭ по математике» : лекции 5–8. – М. :
Педагогический университет «Первое сентября», 2009. – 80 с.
• Распечатай и реши: Математика ОГЭ 2021 (time4math.ru)
• Открытый банк заданий ОГЭ (fipi.ru)



























 mathematics
mathematics








