Similar presentations:
Теория принятия решений. Практика №1
1. ТЕОРИЯ ПРИНЯТИЯ РЕШЕНИЙ ПРАКТИКА №1
ДАЛЬНЕВОСТОЧНЫЙ ФЕДЕРАЛЬНЫЙ УНИВЕРСИТЕТИнститут математики и компьютерных технологий
Департамент информационных и компьютерных систем
ТЕОРИЯ ПРИНЯТИЯ РЕШЕНИЙ
ПРАКТИКА №1
Достовалов В.Н.
© 2023
Владивосток
2023
2. Задача о «двух картошках»
Постановка задачиНекоторая фирма специализируется на производстве пищевых
полуфабрикатов. Подвергая определенной обработке
картофель, она производит три различных продукта:
Д - картофельные дольки
K картофельные кубики
X картофельные хлопья
В начале технологического процесса необработанный картофель
сортируется по размеру и качеству, затем распределяется по
различным поточным линиям. Фирма может закупать картофель
у двух различных поставщиков А и Б. При этом объемы
продуктов Д, K и X, которые можно получить из одной тонны
картофеля первого поставщика, отличаются от объемов
продуктов Д, K и X, получаемых из того же количества картофеля
второго поставщика.
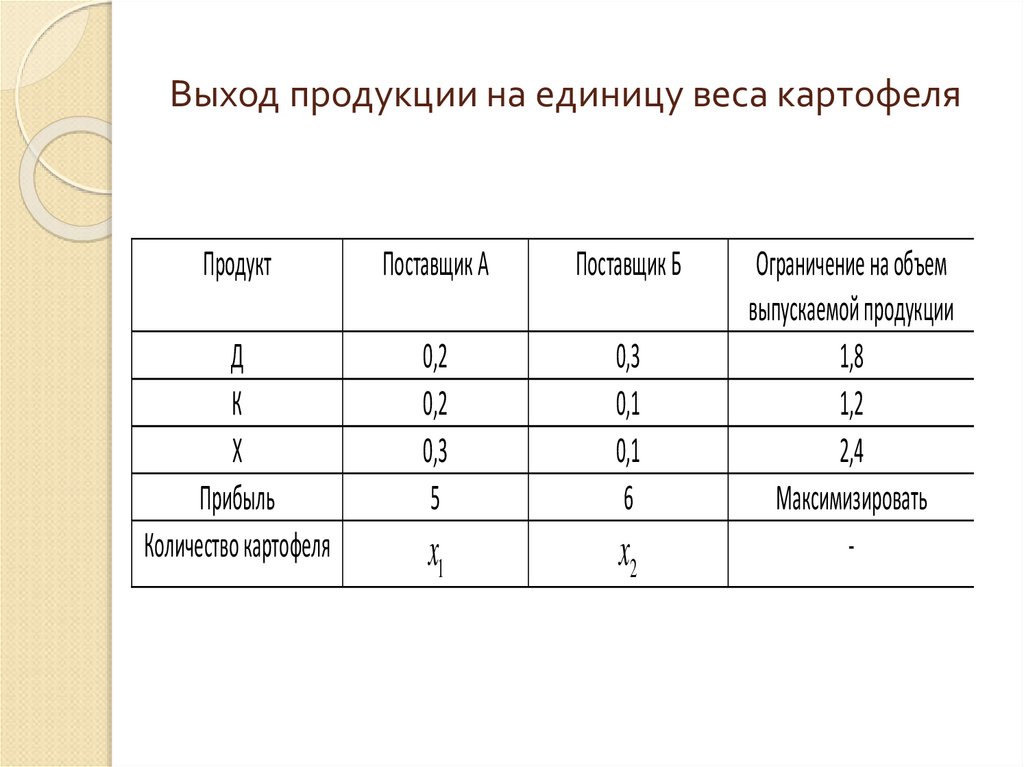
3. Выход продукции на единицу веса картофеля
ПродуктПоставщик А
Поставщик Б
Д
К
Х
Прибыль
Количество картофеля
0,2
0,2
0,3
5
0,3
0,1
0,1
6
x1
x2
Ограничение на объем
выпускаемой продукции
1,8
1,2
2,4
Максимизировать
-
4.
Ограниченияпродукт Д не может выпускаться в количестве, превышающем 1,8 т
продукт К не может выпускаться в количестве, превышающем 1,2 т
продукт Х не может выпускаться в количестве, превышающем 2,4 т
Управляемые переменные
План закупок: ( x1, x2 )
Целевой функционал:
П 5x1 6x2 max
Управляющему фирмой нужно решить следующую задачу: какое
количество картофеля следует закупить у каждого из поставщиков, с
тем, чтобы получить максимально возможную прибыль
5. Ограничения
Продукт Д:Продукт К:
Продукт Х:
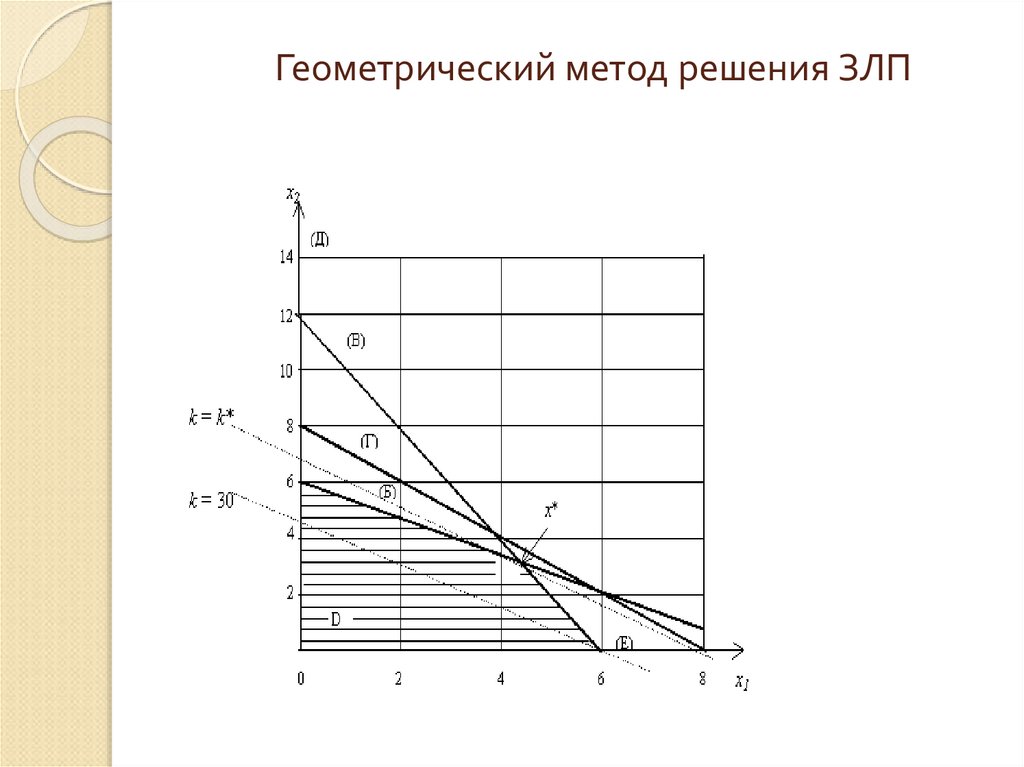
6. Математическая задача
7. Линейные неравенства с двумя переменными
Решением линейного неравенствас двумя переменными называется такая упорядоченная
пара чисел
, которая при подстановке в
неравенство соответственно, обращает его в верное
числовое неравенство.
Решить линейное неравенство с двумя неизвестными
означает найти множество всех его решений.
8. Алгоритм графического метода решения линейных неравенств с двумя неизвестными
В исходном неравенстве заменить знак неравенства на равенство.Получится линейное уравнение с двумя неизвестными,
соответствующее исходному неравенству
Построить на координатной плоскости прямую, которая служит
графиком полученного уравнения.
Определить, какая из полученных полуплоскостей является
множеством решений исходного неравенства. Для этого взять
произвольную точку плоскости, не принадлежащую данной
прямой. Удобно брать в качестве такой точки начало координат,
если построенная прямая не проходит через нее. Подставить
координаты выбранной точки в исходное неравенство, проверить
истинность полученного числового неравенства. Если
неравенство истинно, то решением неравенства является
полуплоскость, содержащая выбранную точку, в противном случае
-полуплоскость, не содержащая выбранную точку. Показать
штриховкой графическое решение неравенства.
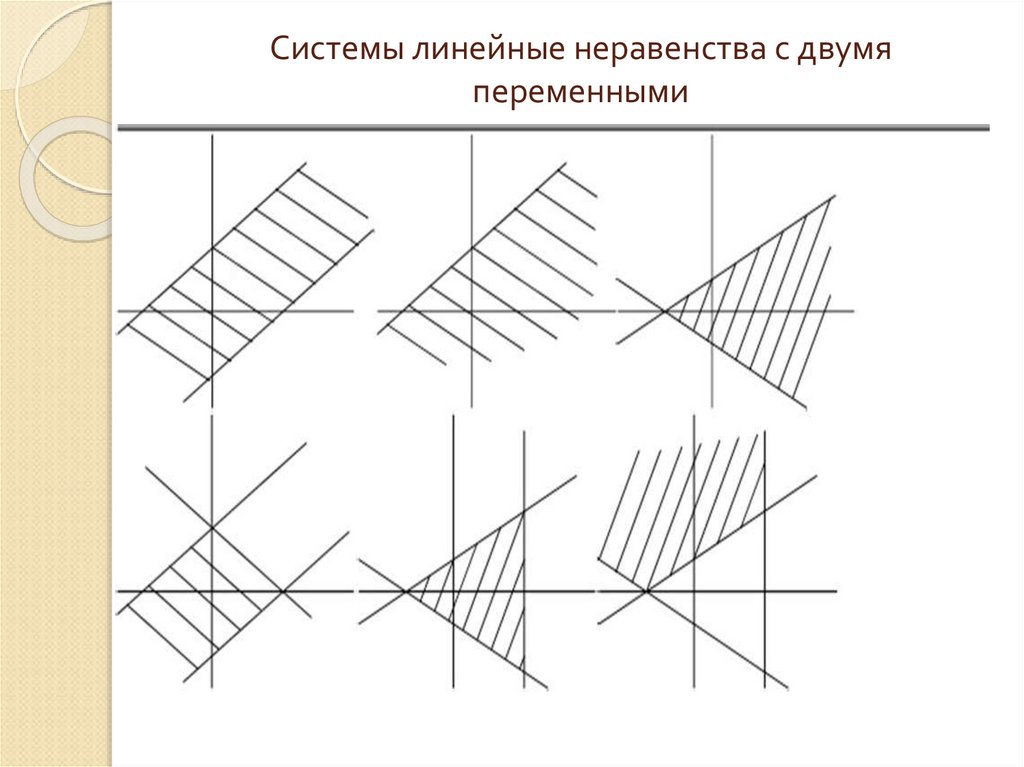
9. Системы линейные неравенства с двумя переменными
Решением системы линейных неравенствс двумя переменными называется такая упорядоченная
пара чисел
, которая при подстановке в
неравенства соответственно, обращает их в верные
числовые неравенства.
Решить систему линейных неравенств с двумя
неизвестными означает найти множество всех его
решений (полиэдр)
Графический метод решения системы неравенств подразумевает построение
на координатной плоскости множества решений каждого неравенства.
Пересечение этих множеств решений и дает решение системы неравенств.








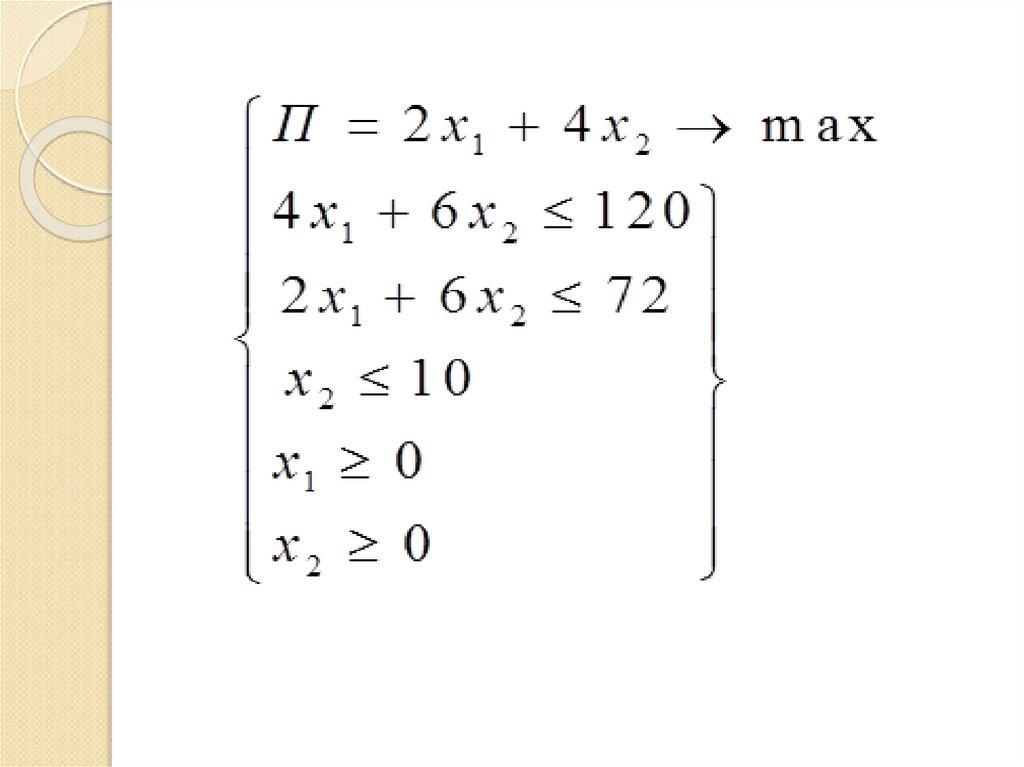
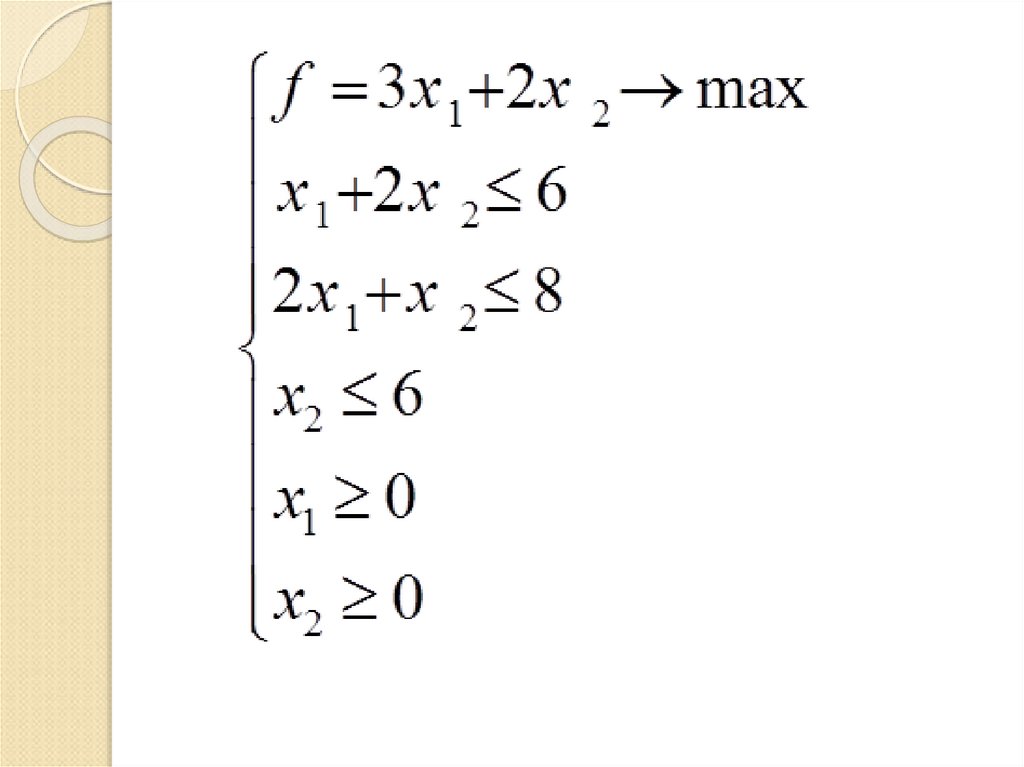
 management
management








