Similar presentations:
Математика Средневековой Европы. Математика эпохи Возрождения
1.
Математика Средневековой Европы.Математика эпохи Возрождения.
Работу выполнила Стрепятская С.С.
Группа: Б-3101
Направление: Дизайн интерьера
2.
Математика Средневековой ЕвропыВключала изучение природы, математики и естественной
философии в средневековой Европе. После падения
Западной Римской империи и снижения уровня знаний
греческого языка христианская Западная Европа была
отрезана от важного источника древних знаний. Однако ко
времени Высокого Средневековья регион сплотился и был на
пути к тому, чтобы вновь занять лидирующие позиции в
области научных открытий .
Свое название «средние века» данный исторический период
получил от своих современников в христианской Европе, как
период между первым и вторым пришествиями Бога.
Ожидание скорого конца света накладывало отпечаток на
образ жизни и мышления людей.
Исторический период: 500-1500 гг.
3.
Математика эпохи ВозрожденияВек XV и XVI, вошли в историю Европы под названием «эпохи
Возрождения», при этом имеется в виду возрождение того высокого
уровня культуры, который был достигнут в античном мире. На самом
же деле эта эпоха характеризуется гораздо более глубокими
преобразованиями в жизни всего общества: именно в это время еще в
недрах феодального строя возникает новый общественный строй —
буржуазное общество.
В промышленности появляются мануфактуры, требующие
технических усовершенствований и изобретений. Тогда же появляются
в Европе компас, часы и порох, дешевая бумага и книгопечатание.
Гигантски возрастает торговля, приведшая к исключительному росту
мореплавания и к великим географическим открытиям. Бумага и
книгопечатание делают научные знания необходимым элементом
общественной жизни.
Исторический период: 1500-1600 гг.
4.
Тезисы5.
Леонардо ПизанскийПервым крупным математиком средневековой
Европы стал в XIII веке Леонардо Пизанский,
известный под прозвищем Фибоначчи.
Невозможно представить современный
бухгалтерский и вообще финансовый учет без
использования десятичной системы счисления
и арабских цифр, начало использования
которых в Европе было положено Фибоначчи.
Основной его труд: «Книга абака». Также
известны числа Фибоначчи.
1170-1250
6.
«Книга абака»Книга абака — посвящена
изложению и
пропаганде десятичной
арифметики. Книга вышла
в 1202г.
Далее идут разнообразные
приложения и решение
уравнений.
Часть задач — на суммирование
рядов. В связи с контролем
вычислений по
модулю приводятся признаки
делимости на 2, 3, 5, 9. Изложена
содержательная теория
делимости, в том
числе наибольший общий
делитель и наименьшее общее
кратное.
7.
Числа ФибоначчиЧисла Фибоначчи-элементы числовой последовательности:
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987,
1597, 2584, 4181, 6765, 10946…
В которой каждое последующее число равно сумме двух
предыдущих цифр. Последовательность чисел Фибоначчи
{Fn} задается линейным рекуррентным
соотношением:
8.
Использование золотого сечения интерьере9.
Лука ПачолиНаибольших успехов математики Европы
XV—XVI вв. добились и в
области алгебры. Крупнейшим
Европейским алгебраистом XV в. был
итальянец Лука Пачоли . Основным трудом
Пачоли была «Сумма знаний по арифметике,
геометрии, отношениям
и пропорциональности»,
изданная в Венеции в 1494 г.
1445-1517
10.
В первой половине XVI в. благодаря усилиям итальянскихматематиков в алгебре происходят крупные сдвиги,
сопровождаемые весьма драматическими событиями.
Профессор Болонского университета Сципион Даль Ферро
(1465-1526) находит общее решение уравнения третьей
степени но держит его в секрете, ибо оно представляет
большую ценность на соревнованиях по решению задач,
которые тогда широко практиковались в Италии. Перед
смертью он открывает секрет своему ученику Фиоре. В 1535
Фиоре вызывает на соревнование талантливейшего
математика Никколо Тарталью (1499-1557), который, зная,
что Фиоре обладает способом решения кубического
уравнения, прилагает максимум усилий и сам находит
решение! Тарталья побеждает на соревновании, но также
держит свое открытие в секрете. Наконец, на сцене
появляется Джероламо Кардано (1501-1576).
11.
Он тщетно пытается найти алгоритм решения кубическогоуравнения и в 1539 г. обращается к Тарталье с просьбой поведать
ему тайну. Взяв с Кардано «священную клятву» молчания,
Тарталья частично и в не слишком вразумительной форме
приоткрывает для него завесу. Кардано не удовлетворяется и
прилагает усилия, чтобы ознакомиться с рукописью покойного
Даль Ферро. Это ему удается, и в 1545 г. он публикует книгу, в
которой сообщает алгоритм, сводящий решение кубического
уравнения к радикалам («формула Кардано»). В этой же книге
содержится еще одно открытие, сделанное учеником Кардано
Луиджи (Лудовико) Феррари (1522-1565), а именно решение в
радикалах уравнения четвертой степени. Тарталья обвиняет
Кардано в нарушении клятвы, завязывается острая и
продолжительная полемика.
12.
Франсуа ВиетВажнейший шаг к новой
математике сделал
француз Франсуа Виет. Он
окончательно сформулировал
1540-1603
символический метаязык
арифметики — буквенную.
Главным трудом его жизни было
«Введение в искусство анализа»
Виет показал примеры мощи
нового метода, найдя
знаменитые Формула Виета. (формулы, выражающие
коэффициенты многочлена через его корни).
13.
Джон НеперВеликое открытие
XVI века —
изобретение логарифмов (функция, обратная
возведению в степень)
Джоном Непером.
Сложные расчёты
упростились во много раз,
а математика получила
новую неклассическую
функцию с широкой
областью применения.
1550-1617
«Палочки Непера»
14.
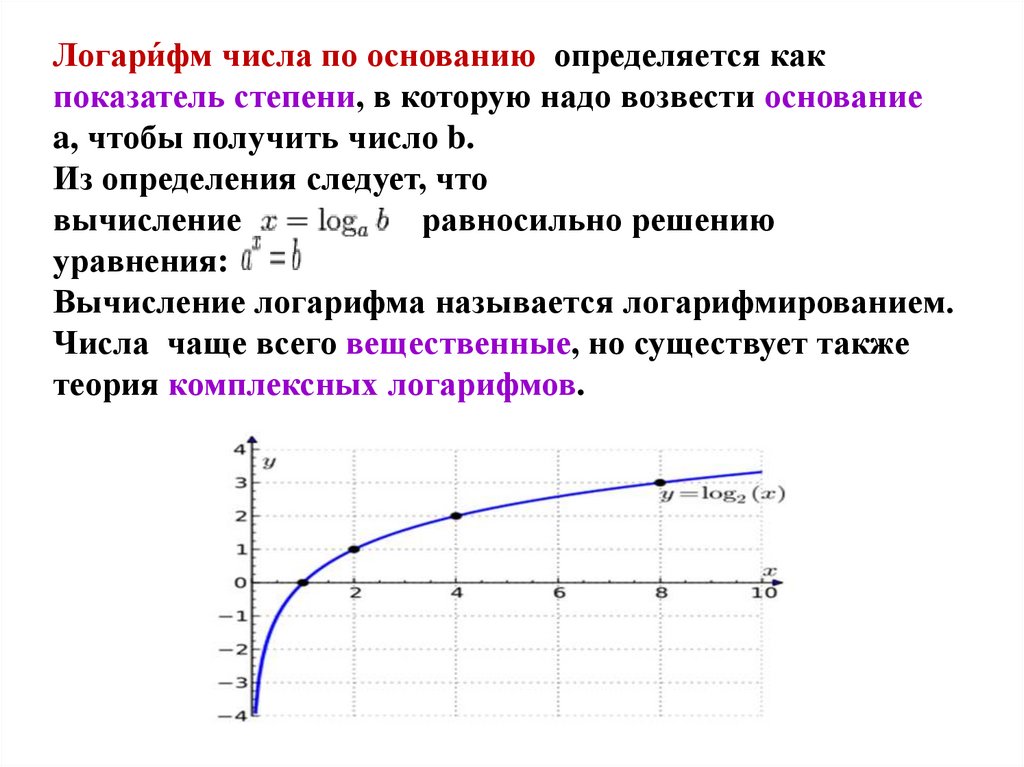
Логари́фм числа по основанию определяется какпоказатель степени, в которую надо возвести основание
a, чтобы получить число b.
Из определения следует, что
вычисление
равносильно решению
уравнения:
Вычисление логарифма называется логарифмированием.
Числа чаще всего вещественные, но существует также
теория комплексных логарифмов.
15.
Создание логарифмической линейкиУильям Отред изобрел в 1630 году два типа
логарифмических линеек-прямоугольную и круглую.
16.
Термины• Арифме́тика— раздел математики, изучающий числа, их
отношения и свойства.
• Линейной рекуррентной последовательностью называется
всякая числовая последовательность, задаваемая линейным
рекуррентным соотношением. Линейные рекуррентные
последовательности иногда называют также возвратными
последовательностями.
• Пропорциональными называются две взаимно зависимые
величины, если отношение их значений остаётся неизменным.
• Метаязы́к — язык, предназначенный для описания другого
языка, называемого объектным языком.
• Вещественные числа — это числа, у которых есть дробная
часть.
17.
Термины• Буржуази́я— социальный класс, владеющий капиталом (в
форме денег, средств производства, земли, патентов или
иного имущества) и существующий за счёт доходов от
этой собственности, в том числе в форме прибыли от
предпринимательской деятельности.
• Анти́чность (от лат. antiquitas «древность, старина») —
термин, означающий греко-римскую древность —
цивилизации Древней Греции и Древнего Рима.
• Логарифмирование – это перевод чисел или уравнений в
логарифмический масштаб или, попросту говоря,
«навешивание» логарифмов.
• Комплексный логарифм — аналитическая функция,
получаемая распространением вещественного логарифма
на всю комплексную плоскость (кроме нуля).
18.
Список литературы• Ю.В.Шевцова Математика в средние века / Ю.В.Шевцова
[Электронный ресурс] // Математика средних веков и эпохи
возрождения. Математика 17 века. : [сайт]. — URL:
http://elibrary.sgu.ru/uch_lit/2225.pdf (дата обращения: 11.09.2023).
• МАТЕМАТИКА ЕВРОПЕЙСКОГО СРЕДНЕВЕКОВЬЯ И ЭПОХИ
ВОЗРОЖДЕНИЯ / [Электронный ресурс] // Студопедия : [сайт]. —
URL: https://studopedia.ru/10_173543_matematika-evropeyskogosrednevekovya-i-epohi-vozrozhdeniya.html (дата обращения:
11.09.2023).
• Математика европейского средневековья и эпохи Возрождения /
[Электронный ресурс] // Helpiks : [сайт]. — URL: https://helpiks.org/1131998.html (дата обращения: 11.09.2023).
• Математика эпохи Возрождения / [Электронный ресурс] // allbest :
[сайт]. — URL: https://revolution.allbest.ru/mathematics/00528759_0.html
(дата обращения: 17.09.2023).
19.
Разгадайте ребус20.
Правильный ответ:Теорема Виета
21.
Разгадайте ребус22.
Правильный ответ:Золотое сечение
23.
Филворд24.
Филворд25.
Математика Средневековой Европы.Математика эпохи Возрождения.
Работу выполнила Стрепятская С.С.
Группа: Б-3101
Направление: Дизайн интерьера
























 mathematics
mathematics history
history








