Вступ до математичного аналізу. Лекція 1

1.

ЛЕКЦІЯ 1
Вступ до математичного аналізу
1. Основні означення і формули
1.1. Поняття та основні характеристики функцій
Одним із основних математичних понять є поняття функції, або функціональної залежності одних величин від інших.
Якщо кожному елементу x із множини X
n
за певним правилом пос-
тавлено у відповідність єдиний елемент y із множини Y
m
, то ця відповід-
ність називається функцією і позначається
y f x .
При цьому функція називається
функцією однієї дійсної змінної, якщо X
,Y
функцією кількох дійсних змінних, якщо X
n
вектор-функцією дійсної змінної, якщо X
,Y
вектор-функцією векторного аргументу, якщо X
;
, n 2, Y
m
n
;
, m 2;
, n 2, Y
m
,m 2.
Якщо X множина комплексних чисел, тоді f дійсна або комплекснозначна функція комплексного аргументу. Взагалі, X та Y не обов’язково числові множини. Якщо X множина функцій, а Y
, то f називають фун-
кціоналом.
Множину X називають областю визначення функції і позначають D f ,
множину всіх у, таких, що y f x називають областю значень функції і позначають E f .
У вступі до математично аналізу розглядають функції однієї дійсної змінної.

2.

Способи задання функцій
1. Аналітичний спосіб, у вигляді формули або рівняння. Прикладом
такого задання є елементарні функції, також функції задані неявно, параметрично або більш складним чином за допомогою різних формул для різних значень
аргументу. Наприклад:
y 3sin 2 x 1,
y 5 y x 1 0,
2 x 8, x 4,
y x 4, 4 x 5,
ln x 4 , x 5.
x 2cos t ,
y 5sin t , t параметр,
2. Графічний спосіб, коли заданий графік функції, тобто множина точок
x, f x площини Oxy , абсциси яких належать області визначення D f функції y f x , а ординати дорівнюють відповідним її значенням. Найчастіше
графіки викреслюються автоматично самописними пристроями або зображуються на екрані дисплея. Такий спосіб задання функції є наглядним, але неточним.
Не для кожної функції можна зобразити її графік. Наприклад, функція
Діріхле
1, якщо х раціональне число,
D x
0, якщо х ірраціональне число
не припускає графічного зображення.
3. Табличний спосіб, коли залежність між змінними задається у вигляді
таблиці, яка містить значення аргументу і відповідні їм значення функції. Наприклад,
х
2
у
0,5 0,476 0,454 0,435 0,417 0,4 0,385 0,37 0,357 0,345 0,333
2,1
2,2
2,3
2,4
2,5
2
2,6
2,7
2,8
2,9
3

3.

Таблицями значень функцій , отриманих дослідним шляхом або в результаті експерименту часто користуються на практиці. Але таблиця не дає всіх
значень функції. Проміжні її значення, які не входять в задану таблицю, можна
найти наближено за допомогою так званої операції інтерполяції функції. Тобто можна побудувати наближену формулу, причому не одну, а от знайти точний аналітичний вираз для функції, заданої таблицею в загальному випадку неможливо.
4. Алгоритмічний (або програмний) спосіб задання функцій широко
використовують у програмуванні. Як правило, цим способом задаються такі
функції, які є розв’язками складних математичних задач. Жодним з попередніх
способів подібні функції задати не можна.
5. Словесний спосіб полягає в тому, що закон, за яким залежно від х обчислюється значення у, виражається словами. Наприклад, функцію у задано
умовою: кожному дійсному числу х ставиться у відповідність найбільше ціле
число, яке не перевищує х. Ця функція, визначена на множині дійсних чисел, називається цілою частиною х і позначається
y x
(читається «ент’є від ікс» від французького слова entire – цілий).
Основні характеристики функцій
Основними характеристиками функції є область визначення
D f , множина значень E f , парність чи непарність, періоди чність, монотонність, опуклість.
Перш за все при дослідженні функції потрібно знайти її область визначення. Якщо для функції, заданої аналітично, D f явно не вказана, тоді її розуміють як множину всіх значень x
, при яких формула y f x має зміст.
Для цього потрібно пам’ятати, що
3

4.

1) y
1
f x 0;
f x
2) y
f x f x 0 ;
3) y log a f x
f x 0 ;
4) y arcsin f x або y arccos f x
f x 1.
Функція y f x називається парною, якщо її область визначення симетрична відносно нуля і для будь-якого x D f виконується рівність
f x f x .
Функція y f x називається непарною, якщо її область визначення симетрична відносно нуля і для будь-якого x D f виконується рівність
f x f x .
Графік парної функції симетричний відносно осі OY , а графік непарної
функції симетричний відносно початку координат. Функція, яка не є парною
або непарною називається функцією загального виду.
Функція y f x називається періодичною з періодом T 0 , якщо для
будь-якого
x D f
значення
x T D f
і
має
місце
рівність:
f x f x kT , k . Найменший із додатних періодів функції називається
основним періодом функції. Наприклад, періодом sin x і cos x є T 2 , а
функції tg x і ctg x мають період T . Функція може бути періодичною, а основного періоду не мати, наприклад, стала функція f x c, c const .
Функція y f x називається обмеженою на проміжку Х, якщо існує таке число M 0 , що f x M для будь-якого x X . Графік обмеженої функції
лежить між прямими y M та y M .
4

5.

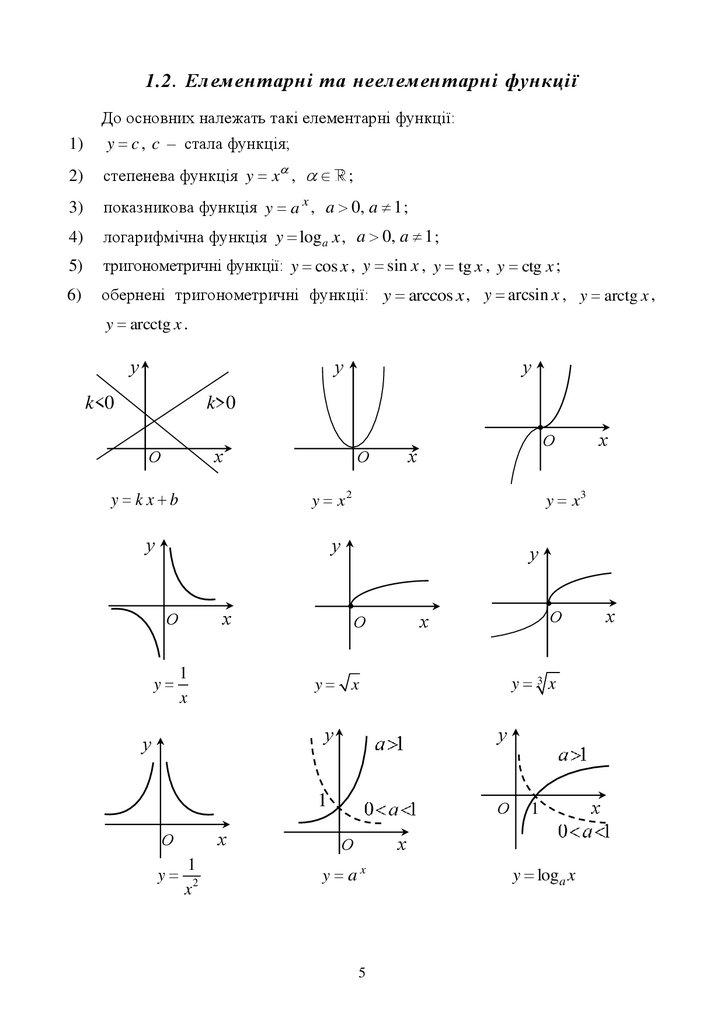
1.2. Елементарні та неелементарні функції
До основних належать такі елементарні функції:
1)
y c , c – стала функція;
2)
степенева функція y x , ;
3)
показникова функція y a x , a 0, a 1 ;
4)
логарифмічна функція y log a x , a 0, a 1 ;
5)
тригонометричні функції: y cos x , y sin x , y tg x , y ctg x ;
6)
обернені тригонометричні функції: y arccos x , y arcsin x , y arctg x ,
y arcctg x .
у
у
k<0
у
k>0
х
О
y x2
у
у
х
О
y
1
x
х
y
1
x2
х
y x3
у
y 3 x
у
у
1
О
1
х
О
y ax
5
х
О
х
О
y x
у
О
х
О
y k x b
О
y log a x
х

6.

у
у
1
1
х
О
-1
y sin x
у
х
О
-1
y cos x
у
у
х
О
y tg x
у
у
х
-1 О
y arctg x
х
1
y arcsin x
y ctg x
у
О
-1 О
х
О
1
х
y arccos x
О
х
y arcctg x
Функція вважається елементарною, якщо вона визначена одним аналітичним виразом, утвореним з основних елементарних функцій за допомогою скінченного числа арифметичних дій та суперпозицій (операцій взяття функції від
функції – утворення складених функцій). Наприклад, функції
y kx b,
y x x , y ln sin x ,
2
cos3 x
y
arcsin 5 x 1
x
є елементарними.
Елементарними також є гіперболічні функції (гіперболічний синус,
гіперболічний косинус, гіперболічні тангенс і котангенс відповідно):
sh x
e x e x
e x e x
sh x
, ch x
, th x
,
2
2
ch x
6
cth x
ch x
.
sh x

7.

Має місце основна гіперболічна тотожність:
ch 2 x sh 2 x 1, x .
у
Наведемо приклади неелементарних функцій:
1
1, x 0,
1) y sgn x 0, x 0,
1, x 0
О
х
х -1
сігнум (знак) числа.
2) y x найбільше ціле число, що не перевищує x (“ентьє” від x ).
3) y x x x дробова частина числа x .
0, x 0,
4) y 1 x
одинична функція Гевісайда.
1, x 0
В більшості випадків значення функції
у
1
в точці x 0 не є важливим.
О
Зазвичай її довизначають значенням 1.
x 2 x3
5) y x
2
3
суми.
xn
n
− функція задана у вигляді
7
х
нескінченої

8.

Теоретичні запитання
1. Що називається функцією однієї дійсної змінної? Що називається областю
визначення та множиною значень функції y f x ?
2. Охарактеризувати основні способи задання функцій. Навести приклади.
3. Записати аналітичний вираз функції, для якої не можна побудувати графік.
4. Перелічити основні характеристики функцій.
5. Які функції називаються парними, непарними? Які особливості цих функцій?
6. Яка функція називається періодичною? Що називається її основним періодом?
Навести приклади періодичних функцій, вказати їх основний період.
7. Яка функція називається обмеженою? Навести приклади обмежених функцій.
8. Перелічити основні елементарні функції.
9. Яка функція називається елементарною а яка неелементарною? Навести приклади.
10. Як визначається функція сігнум ікс? Як визначається функція Гевісайда? Побудувати їх графіки.
Домашнє завдання.
Вміти відповідати на теоретичні запитання.
Розв’язати задачі 1, 2, 3 свого варіанту з індивідуальних завдань РГР.
Зразки розв’язання задачі 1 з РГР
Задача 1. Знайти область визначення функцій
а) y ln x 10 3
1
x 5
,
б) y
Розв’язання. а) y ln x 10 3
arcsin x 3
1
x 5
9 x2
.
Функція визначена за умов, що аргумент логарифма має бути додатним, а
також має бути виключене ділення на нуль. Зауважимо, що корінь кубічний
можна вилучати з будь-якого числа. Ці дві умови мають виконуватись одночасно, тому складемо і розв’яжемо систему:
8

9.

x 10 0,
x 10,
x 5 0
x 5.
Отже, область визначення функції має вид:
D f 10; 5
б) Функція
y
5; .
arcsin x 3
9 x2
визначена, якщо одночасно виконуються дві умови:
1) аргумент арксинуса змінюється в межах від - 1 до 1 включно, тобто
1 x 3 1.
Якщо додати число 3 до всіх частин нерівності, то отримаємо
2 x 4
x 2; 4 .
2) Підкореневий вираз у знаменнику дробу має бути строго додатним:
9 x 2 0.
2
Тобто, x 9 0 x 3 x 3 0 x 3; 3 .
Отже, функція визначена на множині, що є перетином отриманих множин
x 2; 4
3; 3 .
Остаточно отримаємо: D f 2;3 .
Зразки розв’язання задачі 2 з РГР
Задача 2. Дослідити функції на парність та непарність:
1) f x
x3
.
x2 1
Розв’язання. Оскільки знаменник дробу при будь-яких значеннях незалежної змінної х відмінний від нуля, функція визначена на всій числовій осі
D f ; .
9

10.

Замінимо в аналітичному виразі функції кожний x на x :
x 3
x3
x3
f x
f x .
x 2 1 x 2 1 x 2 1
Оскільки отримали, що f x f x , то задана функція є непарною. Її
графік симетричний відносно початку координат.
2) y
3
x arcsin x 1 .
Розв’язання. Легко бачити, що область визначення даної функції не є симетричною відносно нуля, тому функція не може бути парною або непарною.
3
Дійсно, множник
x визначений при будь-якому значенні x , а arcsin x 1
визначений за умови 1 x 1 1 , тобто 0 x 2 . Оскільки D f 0; 2 , то
задана функція загального виду.
3) f x
3 3 .
2
1
x
x
Розв’язання. Область визначення даної функції симетрична відносно нуля: D f ; . Замінимо x на x :
f x
1
2
2
2
1
1
x
3 x 3 3 x 3x 3x 3 x f x .
Виконується рівність f x f x , тому функція є парною.
4) f x ln x x 2 1 .
Розв’язання. Знайдемо область визначення D f заданої функції:
x x 2 1 0,
2
x 1 0.
Оскільки x 2 1 0 для x
, то з урахуванням
x 2 | x | отримаємо
x x 2 1 x x 2 x | x | 0 .
10

11.

Тобто нерівність x x 2 1 0 також виконується для x
. Це означає, що
D f ; є симетричною відносно нуля.
Замінимо x на x :
x 1 x x 1 x
f x ln x x 1 ln x 1 x ln
x 1 x
2
2
2
2
2
ln
x2 1 x2
x2 1 x
ln
1
x2 1 x
ln
x 1 x ln x x 1 f x .
1
2
2
Отже, f x f x , а це означає, що функція є непарною.
Зразки розв’язання задачі 3 з РГР
Задача 3. Побудувати графіки функцій:
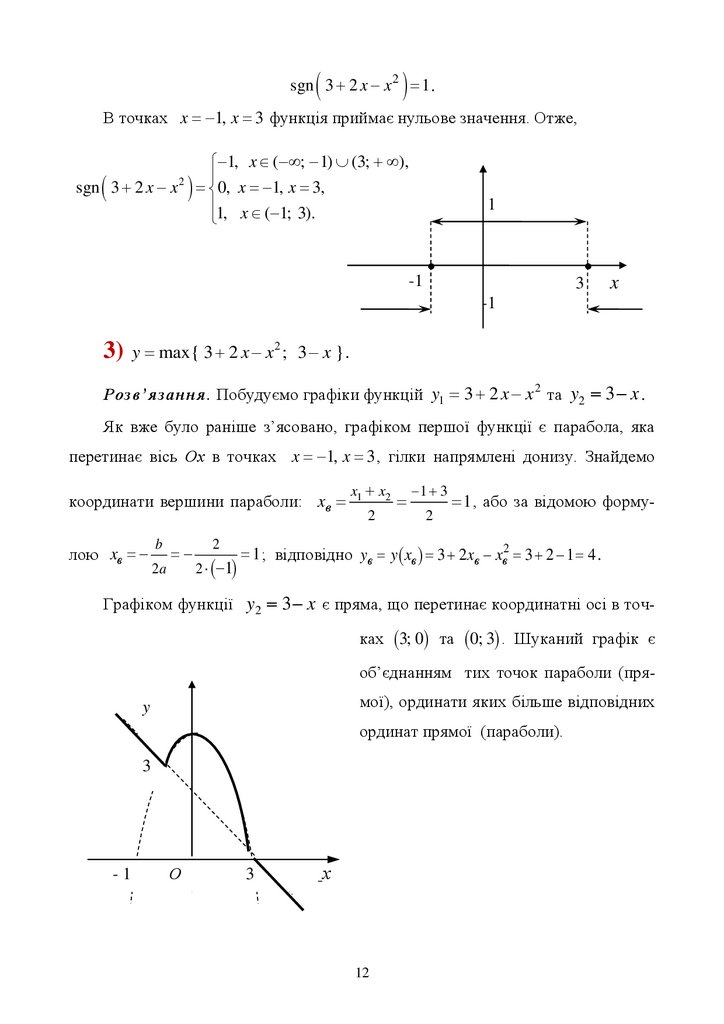
1) y sgn 3 2 x x2 .
Розв’язання. Виходячи з означення функції сігнум (знак числа)
1, x 0,
y sgn x 0, x 0,
1, x 0
потрібно з’ясувати проміжки знакосталості квадратного тричлена 3 2 x x 2 .
Для цього знайдемо його корені:
3 2 x x 2 0 x 2 2 x 3 0 за теоремою Вієта при x 1, x 3.
Графіком функції y 3 2 x x 2 є парабола, яка перетинає вісь Ох в точках x 1, x 3 . Гілки параболи напрямлені донизу, оскільки у квадратному
тричлені коефіцієнт при x 2 від’ємний a 1 0 .
Звідси при x ( ; 1)
(3; ), виконується нерівність 3 2 x x 2 0 , тому
sgn 3 2 x x 2 1 .
При x ( 1; 3) виконується нерівність 3 2 x x 2 0, і тому
11

12.

sgn 3 2 x x 2 1 .
В точках x 1, x 3 функція приймає нульове значення. Отже,
1, x ( ; 1) (3; ),
sgn 3 2 x x 2 0, x 1, x 3,
1, x ( 1; 3).
y
1
-1
3
x
-1
3) y max{ 3 2 x x 2 ; 3 x } .
Розв’язання. Побудуємо графіки функцій y1 3 2 x x 2 та y2 3 x .
Як вже було раніше з’ясовано, графіком першої функції є парабола, яка
перетинає вісь Ох в точках x 1, x 3 , гілки напрямлені донизу. Знайдемо
x x2
координати вершини параболи: xв 1
лою xв
b
2a
2
2 1
2
1 3
2
1 , або за відомою форму-
1 ; відповідно yв y xв 3 2 xв xв2 3 2 1 4 .
Графіком функції y2 3 x є пряма, що перетинає координатні осі в точках 3; 0 та 0; 3 . Шуканий графік є
об’єднанням тих точок параболи (прямої), ординати яких більше відповідних
y
ординат прямої (параболи).
3
-1
О
3
х
12

13.

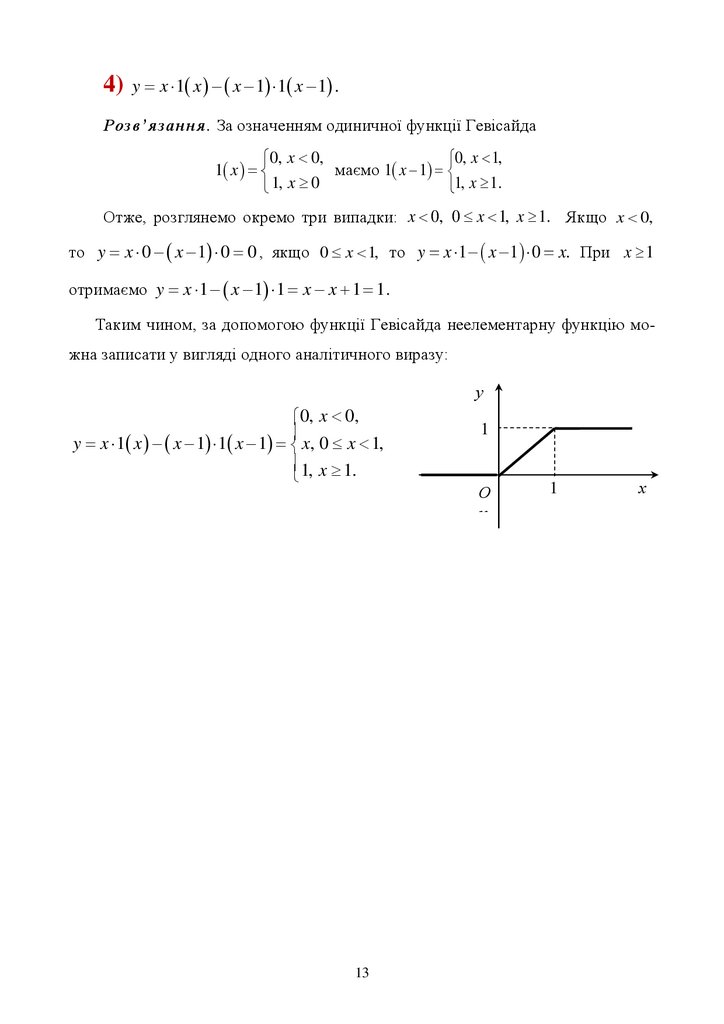
4) y x 1 x x 1 1 x 1 .
Розв’язання. За означенням одиничної функції Гевісайда
0, x 0,
0, x 1,
маємо 1 x 1
1 x
1, x 0
1, x 1.
Отже, розглянемо окремо три випадки: x 0, 0 x 1, x 1. Якщо x 0,
то y x 0 x 1 0 0 , якщо 0 x 1, то y x 1 x 1 0 x. При x 1
отримаємо y x 1 x 1 1 x x 1 1 .
Таким чином, за допомогою функції Гевісайда неелементарну функцію можна записати у вигляді одного аналітичного виразу:
у
0, x 0,
y x 1 x x 1 1 x 1 x, 0 x 1,
1, x 1.
1
О
х
13
1
х