Статика. Связи и реакции связей

1. СТАТИКА

2.

Статика – это раздел теоретической механики, в котором изучаются условия равновесия материальных объектов
(тел) под действием прилагаемых сил и методы эквивалентного преобразования систем сил, приведения их к более
простому виду.
Под равновесием понимают состояние покоя или равномерное, прямолинейное и поступательное движение по
отношению к неподвижной системе координат.
Все разнообразие материальных объектов моделируется: материальной точкой, системой материальных точек и
абсолютно твердым телом.
Материальной точкой называют простую модель материального объекта, размеры которого настолько малые,
что ими можно пренебрегать при изучении того или иного движения. То есть – это геометрическая точка, которая
имеет массу.
Система материальных точек – это совокупность материальных точек, движение и положение каждой из
которых зависит от движения и положения всех остальных точек.
Абсолютно твердым телом (в дальнейшем твердым телом) называют систему материальных точек,
расстояния между которыми остаются все время неизменными.

3.

Сила – это векторная величина, которая является мерой механического взаимодействия между
материальными объектами.
Она характеризуется:
•модулем,
•направлением,
•точкой приложения.
Точка приложения силы и ее направление определяют линию действия силы.

4.

.
Связи и реакции связей
Свободное
тело
–
свобода
перемещений
ограничивается никакими другими телами.
Несвободное
телами.
тело
–
его
движение
ограничено
тела
не
другими
Связь – тело, ограничивающее свободу перемещений объекта.
Реакция связи – сила, действующая на объект со стороны
связи.
Принцип освобождаемости от связи – несвободное тело можно
рассматривать как свободное, если отбросить связи и
заменить их действие соответствующими реакциями

5.

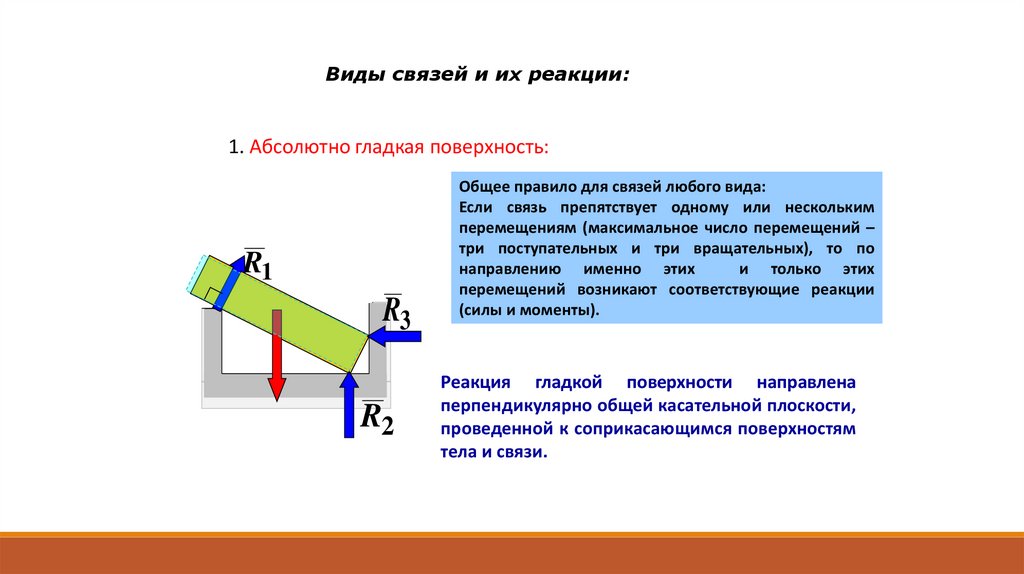
Виды связей и их реакции:
1. Абсолютно гладкая поверхность:
R1
R3
R2
Общее правило для связей любого вида:
Если связь препятствует одному или нескольким
перемещениям (максимальное число перемещений –
три поступательных и три вращательных), то по
направлению именно этих
и только этих
перемещений возникают соответствующие реакции
(силы и моменты).
Реакция гладкой поверхности направлена
перпендикулярно общей касательной плоскости,
проведенной к соприкасающимся поверхностям
тела и связи.

6.

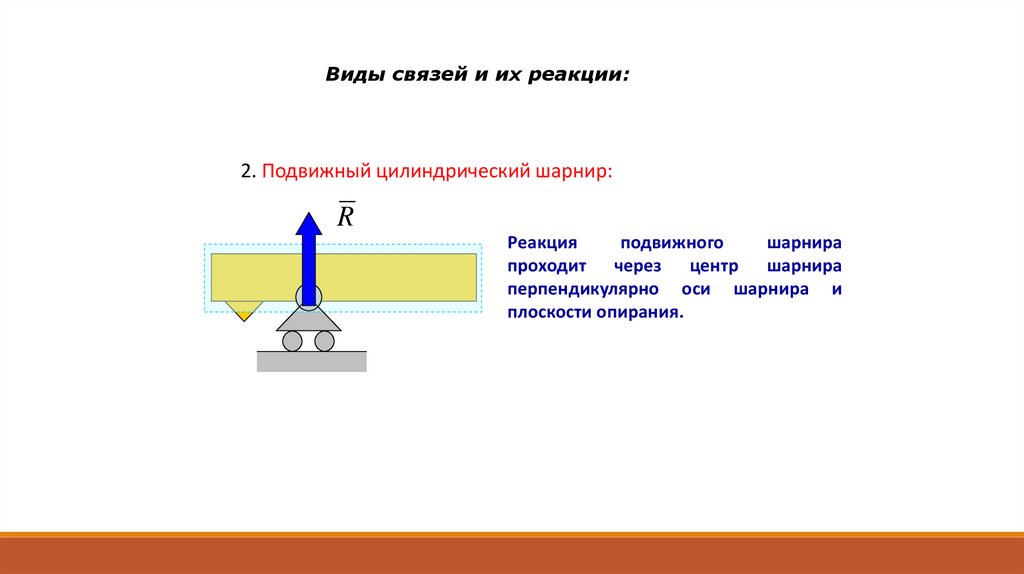
Виды связей и их реакции:
2. Подвижный цилиндрический шарнир:
R
Реакция
подвижного
шарнира
проходит через центр шарнира
перпендикулярно оси шарнира и
плоскости опирания.

7.

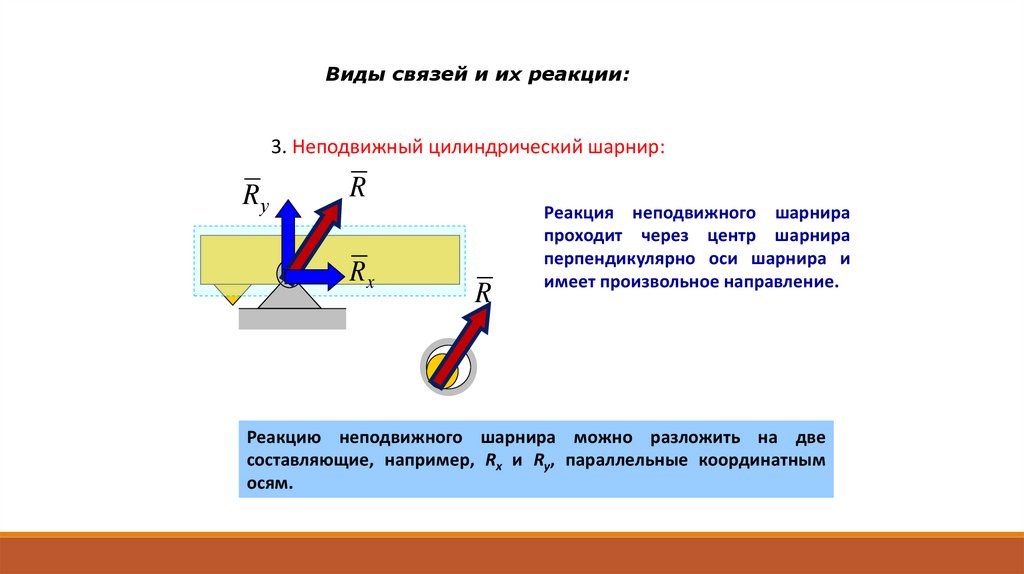
Виды связей и их реакции:
3. Неподвижный цилиндрический шарнир:
Rу
R
Rx
R
Реакция неподвижного шарнира
проходит через центр шарнира
перпендикулярно оси шарнира и
имеет произвольное направление.
Реакцию неподвижного шарнира можно разложить на две
составляющие, например, Rx и Ry, параллельные координатным
осям.

8.

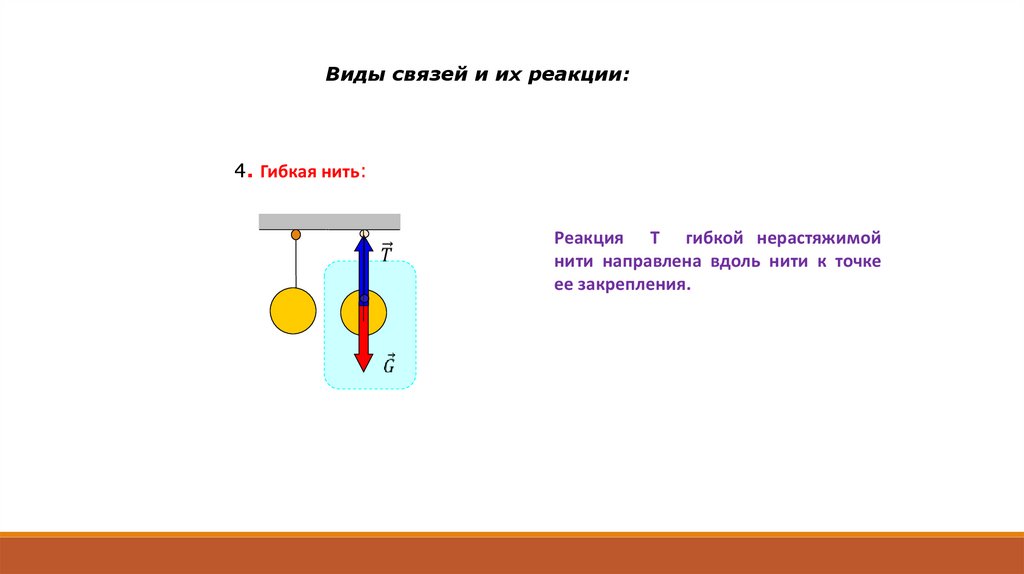
Виды связей и их реакции:
4. Гибкая нить:
Реакция T гибкой нерастяжимой
нити направлена вдоль нити к точке
ее закрепления.

9.

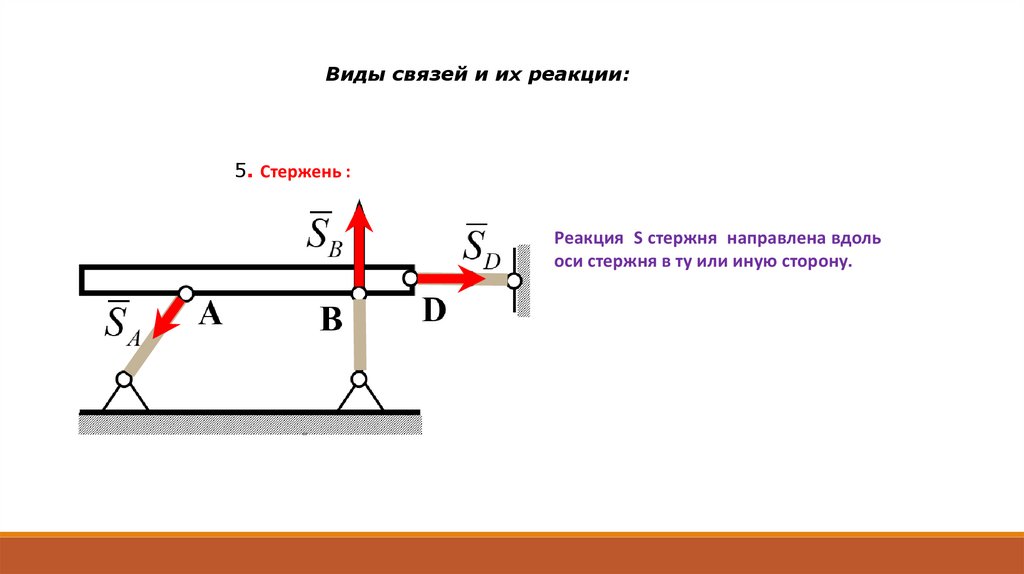
Виды связей и их реакции:
5. Стержень :
Реакция S стержня направлена вдоль
оси стержня в ту или иную сторону.

10.

Виды связей и их реакции:
6. Неподвижный сферический шарнир:
Rz
R
Реакция неподвижного сферического
шарнира проходит через центр
шарнира и имеет произвольное
направление в пространстве.
Ry
Rx
Реакцию неподвижного сферического
шарнира можно разложить на три
составляющие, например, Rx, Ry, Rz,
параллельные координатным осям.

11.

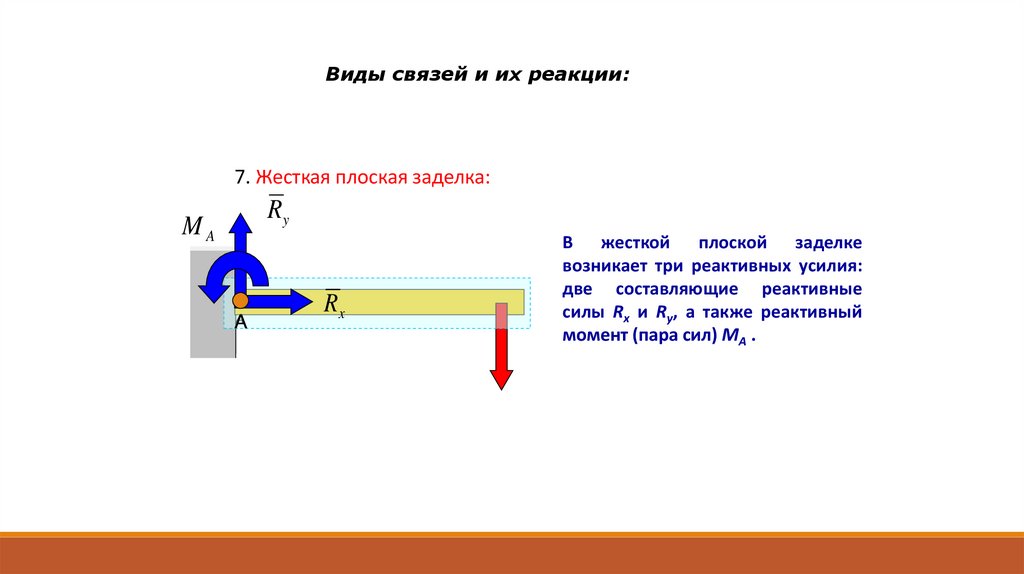
Виды связей и их реакции:
7. Жесткая плоская заделка:
Ry
MA
A
А
Rx
В жесткой плоской заделке
возникает три реактивных усилия:
две составляющие реактивные
силы Rx и Ry, а также реактивный
момент (пара сил) MA .

12.

Система сходящихся сил (ССС) − это система сил, линии действия которых пересекаются в одной точке
F2
F1
F3
F4

13.

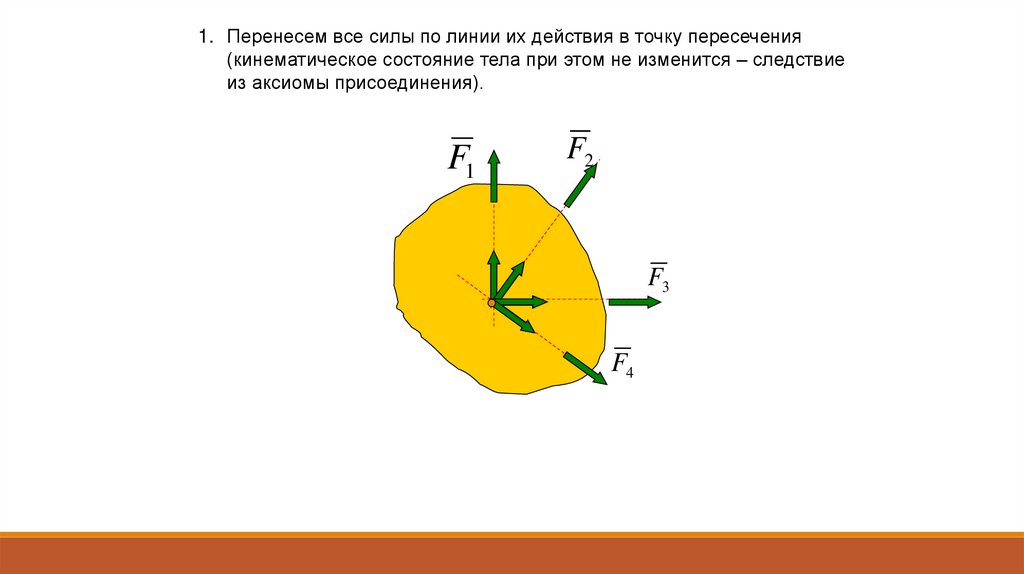
1. Перенесем все силы по линии их действия в точку пересечения
(кинематическое состояние тела при этом не изменится – следствие
из аксиомы присоединения).
F1
F2
F3
F4

14.

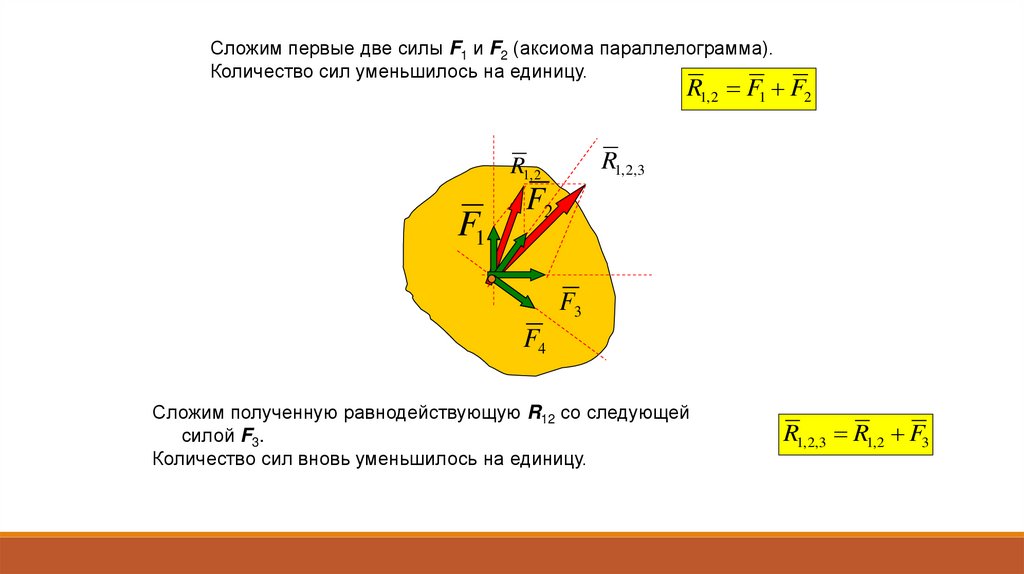
Сложим первые две силы F1 и F2 (аксиома параллелограмма).
Количество сил уменьшилось на единицу.
R1, 2 F1 F2
R1, 2,3
R1, 2
F1
F2
F3
F4
Сложим полученную равнодействующую R12 со следующей
силой F3.
Количество сил вновь уменьшилось на единицу.
R1, 2,3 R1, 2 F3

15.

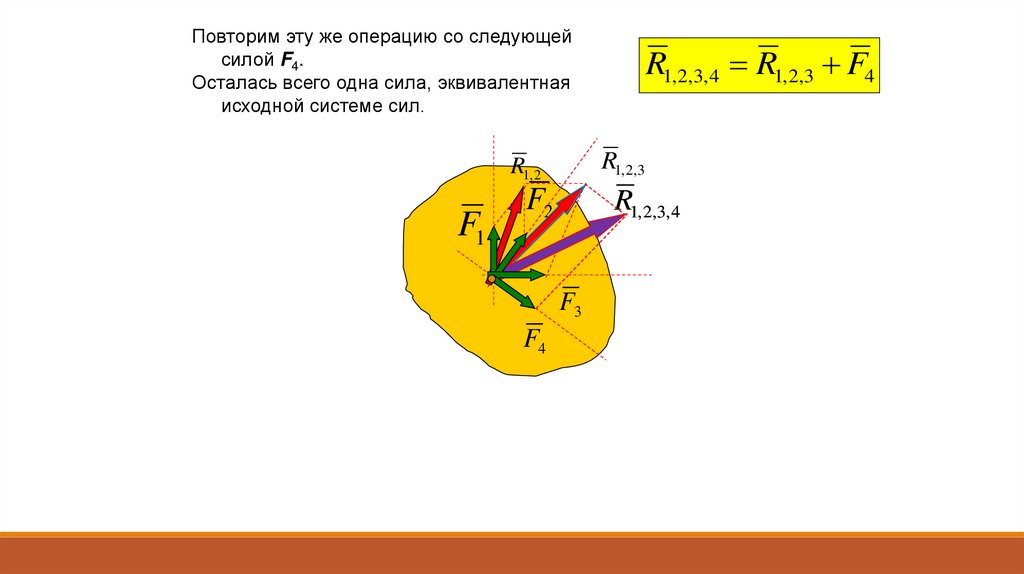
Повторим эту же операцию со следующей
силой F4.
Осталась всего одна сила, эквивалентная
исходной системе сил.
F1
R1, 2,3, 4 R1, 2,3 F4
R1, 2
R1, 2,3
F2
R1, 2,3, 4
F3
F4

16.

F2
F1
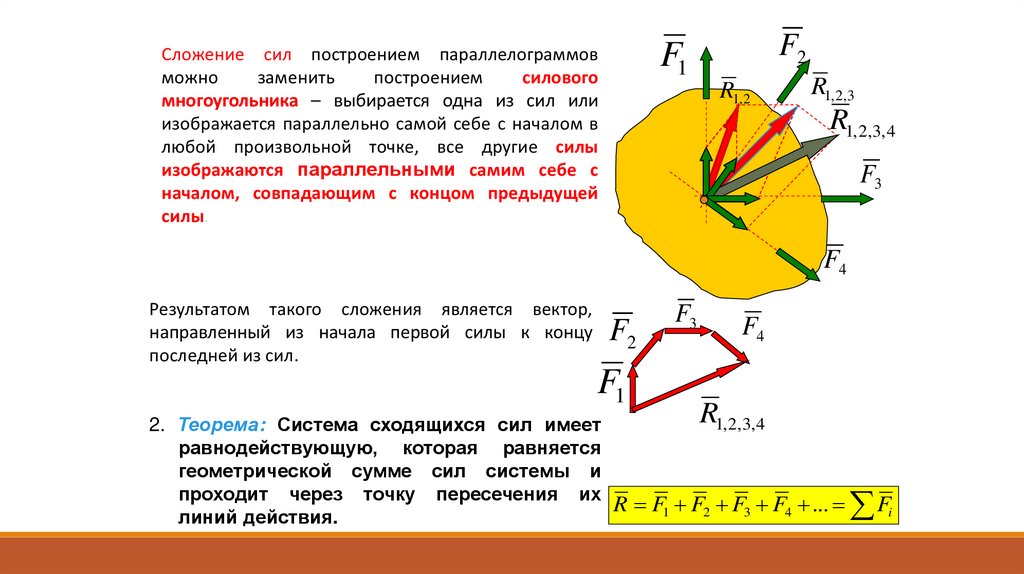
Сложение сил построением параллелограммов
можно
заменить
построением
силового
многоугольника – выбирается одна из сил или
изображается параллельно самой себе с началом в
любой произвольной точке, все другие силы
изображаются параллельными самим себе с
началом, совпадающим с концом предыдущей
силы.
R1, 2
R1, 2,3
R1, 2,3, 4
F3
F4
Результатом такого сложения является вектор,
направленный из начала первой силы к концу
последней из сил.
F2
F3
F4
F1
R1, 2,3, 4
2. Теорема: Система сходящихся сил имеет
равнодействующую, которая равняется
геометрической сумме сил системы и
проходит через точку пересечения их
R F1 F2 F3 F4 ...
линий действия.
F
i

17.

Плоская произвольная система сил – силы лежат в одной плоскости и их
линии действия не пересекаются в одной точке.
Момент силы относительно точки на плоскости – алгебраическая
величина, равная
произведению модуля силы на плечо, взятая
со знаком + (плюс), если вращение плоскости
под действием
силы происходит против часовой стрелки,
и со знаком – (минус)
в противном случае.
Плечо силы – длина перпендикуляра, опущенного из точки на линию действия силы.
F
h
A
M A (F ) F h

18.

В общем случае плоская произвольная система сил приводится к одной силе,
называемой главным вектором и к паре с моментом, равным главному моменту всех сил
системы относительно центра приведения:
- главный вектор,
*
R Fi
- главный момент.
M M A M iA
Уравнения равновесия (I форма) получаются
в виде системы трех уравнений из условий
равновесия с использованием выражений
для проекций главного вектора:
X i 0;
Yi 0;
M iA 0
Существуют еще две формы уравнений
равновесия (II и III формы):
X i 0;
M iB 0;
M iA 0
M iC 0;
M iB 0;
M iA 0

19.

Определение равнодействующей системы сходящихся сил методом проекций и расчет реакций связи
Последовательность действий
1.Расставить реакции связей
2.Найти проекции всех сил
3.Составить уравнения равновесия системы
4.Рассчитать реакции связей
5.Выполнить проверку расчетов

20.

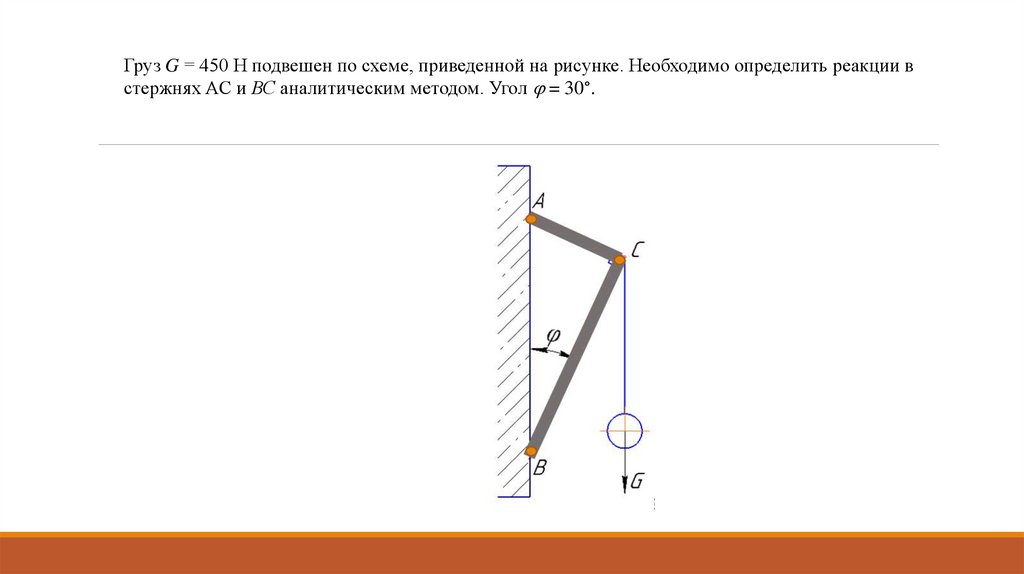
Груз G = 450 Н подвешен по схеме, приведенной на рисунке. Необходимо определить реакции в
стержнях АС и ВС аналитическим методом. Угол = 30°.

21.

1. Расставить реакции связей

22.

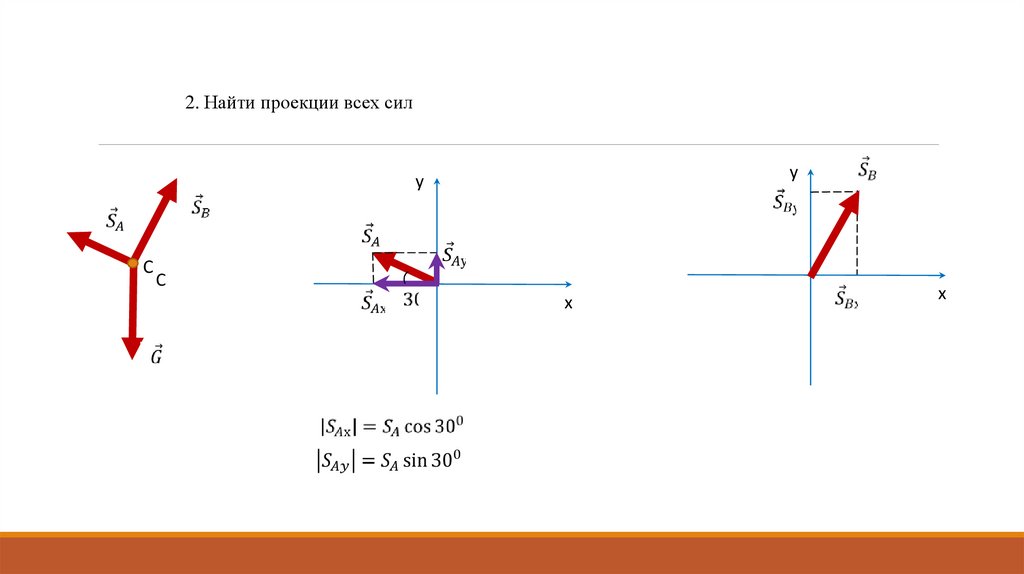
2. Найти проекции всех сил
у
у
С
С
х
х

23.

2. Найти проекции всех сил
у
х

24.

3. Составить уравнения равновесия системы
у
х

25.

4. Рассчитать реакции связей

26.

4. Рассчитать реакции связей

27.

5. Выполнить проверку расчетов

28.

Расчет балочных систем
1. Расставить реакции связей
2. Найти проекции сил при необходимости
3. Рассчитать силу Q
4. Составить расчетную схему
5. Составить уравнения равновесия
6. Рассчитать реакции опор
7. Выполнить проверку расчетов

29.

Балка с шарнирными опорами в точках А и В нагружена, как показано на рисунке, моментом
М=50 Нм, сосредоточенной силой F=25 Н и равномерно распределенной нагрузкой
интенсивностью q= 10 Н/м Определить реакции опор.
6м
5м
4м

30.

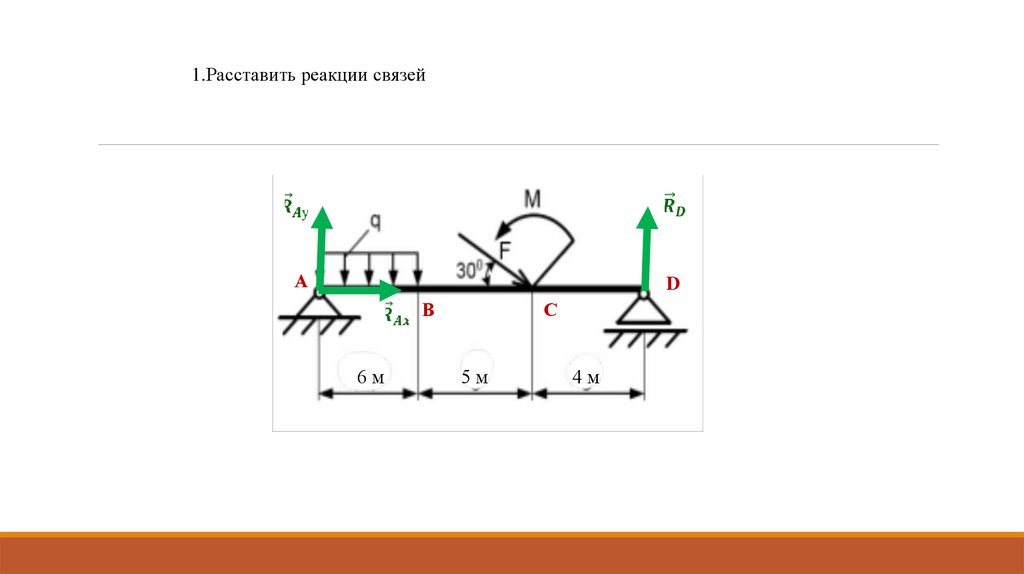
1.Расставить реакции связей
А
D
В
6м
С
5м
4м

31.

2. Найти проекции сил при необходимости
у
х

32.

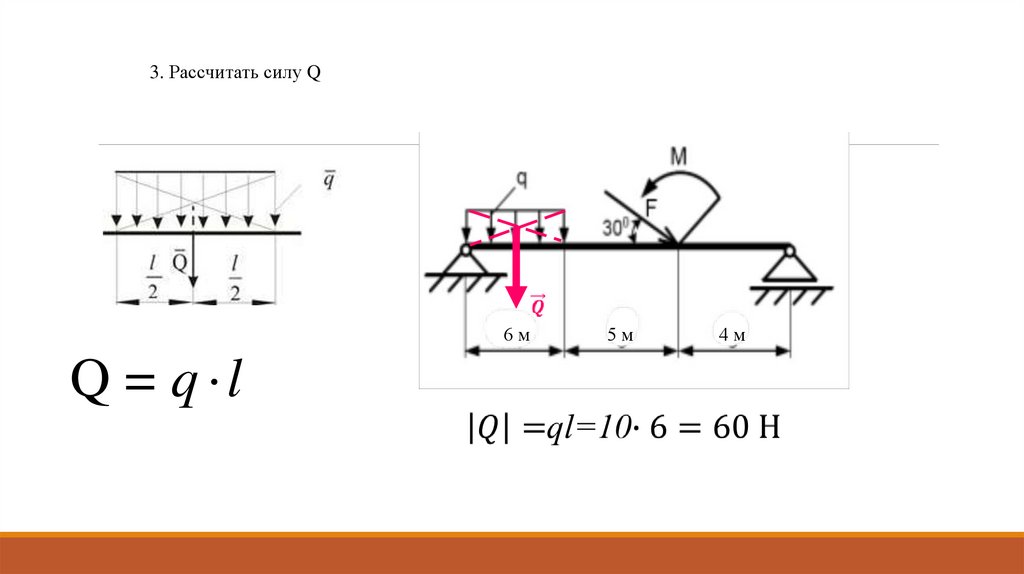
3. Рассчитать силу Q
Q = q l
6м
5м
4м

33.

4. Составить расчетную схему
М
А
D
В
6м
С
5м
4м

34.

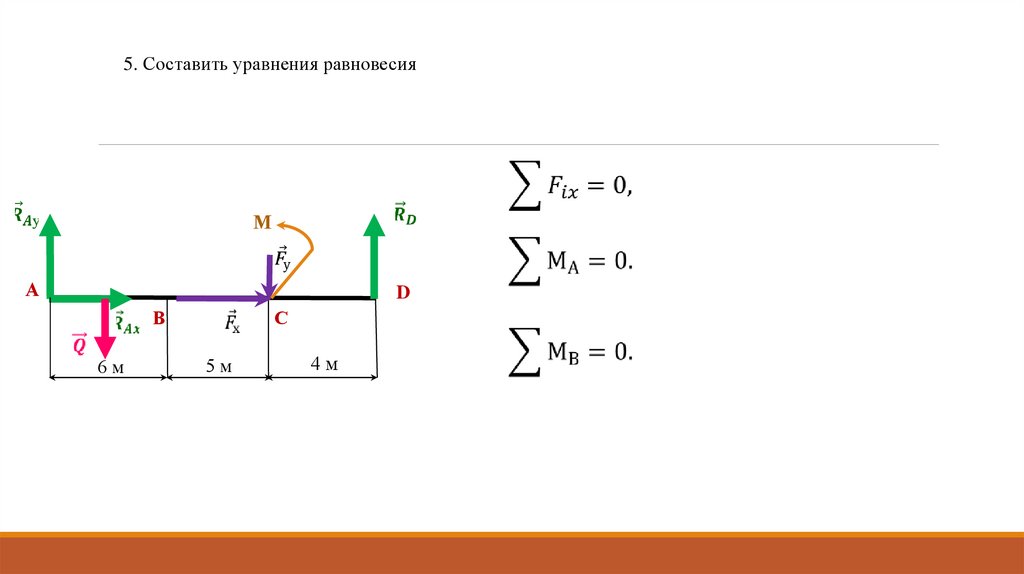
5. Составить уравнения равновесия
М
А
D
В
6м
С
5м
4м

35.

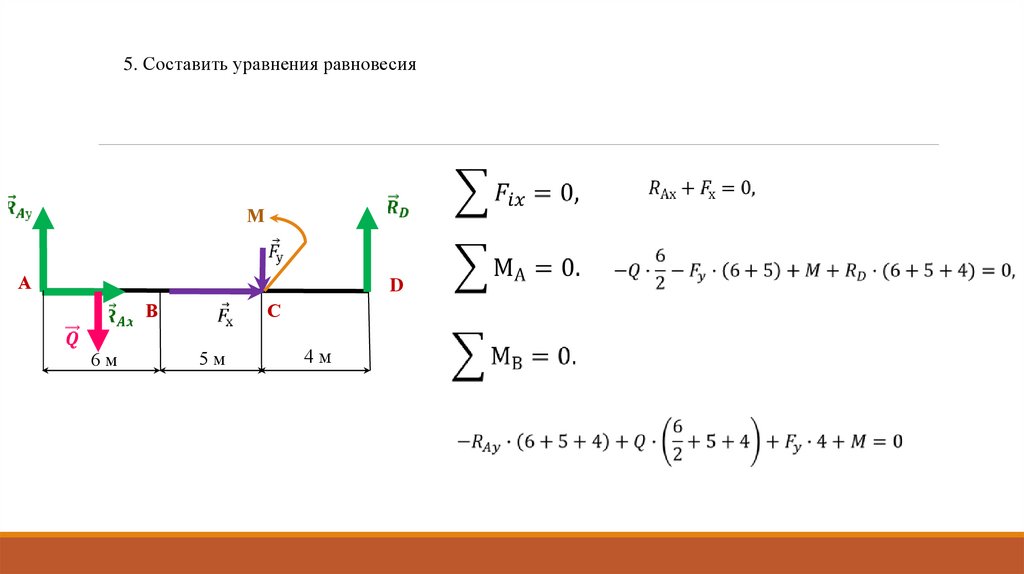
5. Составить уравнения равновесия
М
А
D
В
6м
С
5м
4м

36.

6. Рассчитать реакции опор

37.

7. Выполнить проверку расчетов
М
А
D
В
6м
С
5м
4м