Similar presentations:
Рациональные числа. Закрепление темы
1.
2.
3.
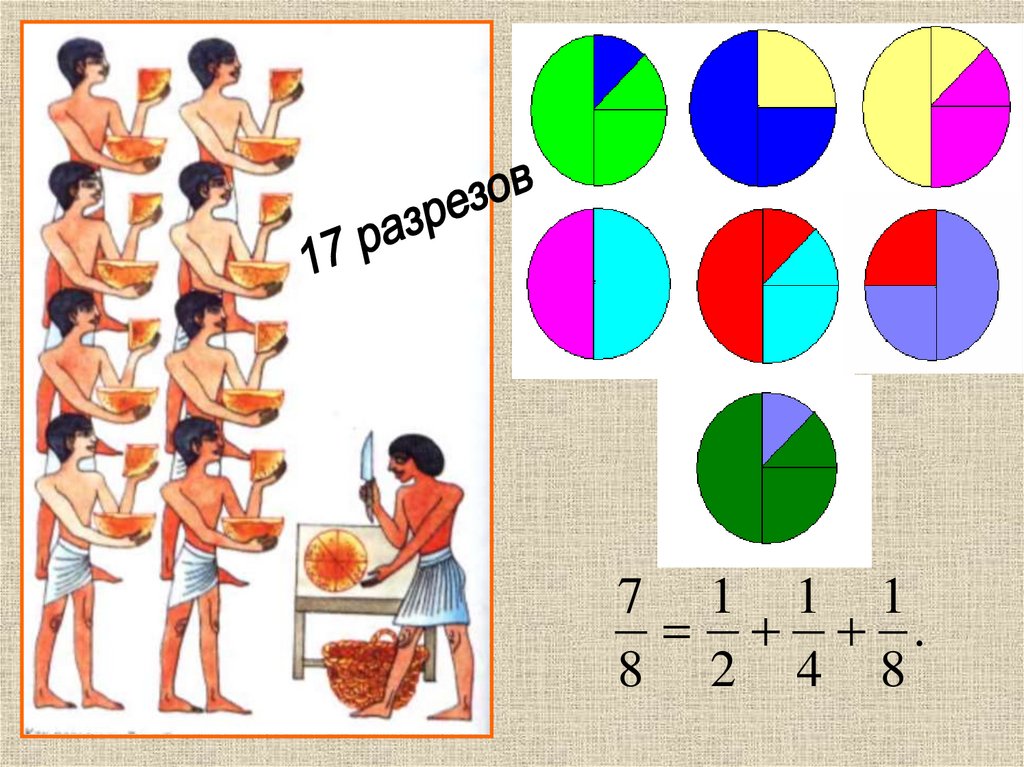
7 1 1 1.
8 2 4 8
4.
1)2)
3)
4)
1
2
2
2:6
2 11
3
2
4
5)
6)
7)
8)
2
2
3
2 2,5
2
2:
7
5
2
6
1. Какие числа называют рациональными?
2. Покажите, что числа 0,33; 3,5; 1 3 ; 7 5 ; 11
4
6
являются рациональными.
5.
№ 1193 (устно)6.
1) № 1179 (б,в)2) №1181 (устно)
3) № 1184
4) 1182 (б, г, е)
5) Выразить числа
8
19
4 в виде приближенного значения
,
, 5
15 36
33
дроби до тысячных (самост.)
6) С помощью МК перевести обыкновенную дробь в десятичную
7) Преобразовать бесконечную периодическую десятичную дробь в
обыкновенную :
0, (5), 0, (7), 0, (37), 0, (338).
7.
(преобразование бесконечных периодическихдесятичных дробей в обыкновенные)
1) нужно в числитель «поставить» «период»
бесконечной десятичной периодической дроби;
2) в знаменатель – число девяток, равное
количеству цифр периода.
5
7
37
338
0, (5) , 0, (7) , 0, (37)
, 0, (338)
.
9
9
99
999
8.
Выразите в виде десятичной или периодическойдроби числа
1 вариант –
2 вариант –
3
7
16
7
3
; 0,35,; 0,(048),
; 1 1,3(18),
;
. 0,024
0,6,
5 20 333
22 125
1 19
29
17
3
;
; 0,1(306),
; 1 1,(51),
;
. 0,012
0,2, 0,475,
5 40 222
33 250
9.
1. Когда обыкновенную дробь можно записать в видеконечной десятичной дроби?
2. Когда несократимую обыкновенную дробь нельзя
записать конечной десятичной дробью? Какой
десятичной дробью можно выразить данную
обыкновенную дробь?
3. Не выполняя деления, скажите, конечной или
бесконечной десятичной дробью можно выразить
данные обыкновенные дроби?
3
7
1
13
41
17
а) ; б ) ; в) ; г )
; д)
; е)
;
5
4
6
26
49
20
31
2
6
1
8
ж) ; з) ; и ) ; к )
; л) .
80
6
9
123
75
10.
п.37, №№ 1197, 1199, 1200(б).Дополнительное задание:
1. Сравните дроби
23 2323 232323
,
,
.
99 9999 999999
2. Запишите в порядке возрастания дроби
3001
,
5001
3
,
5
301
,
501
31
.
51










 mathematics
mathematics