Обратная задача дифракции

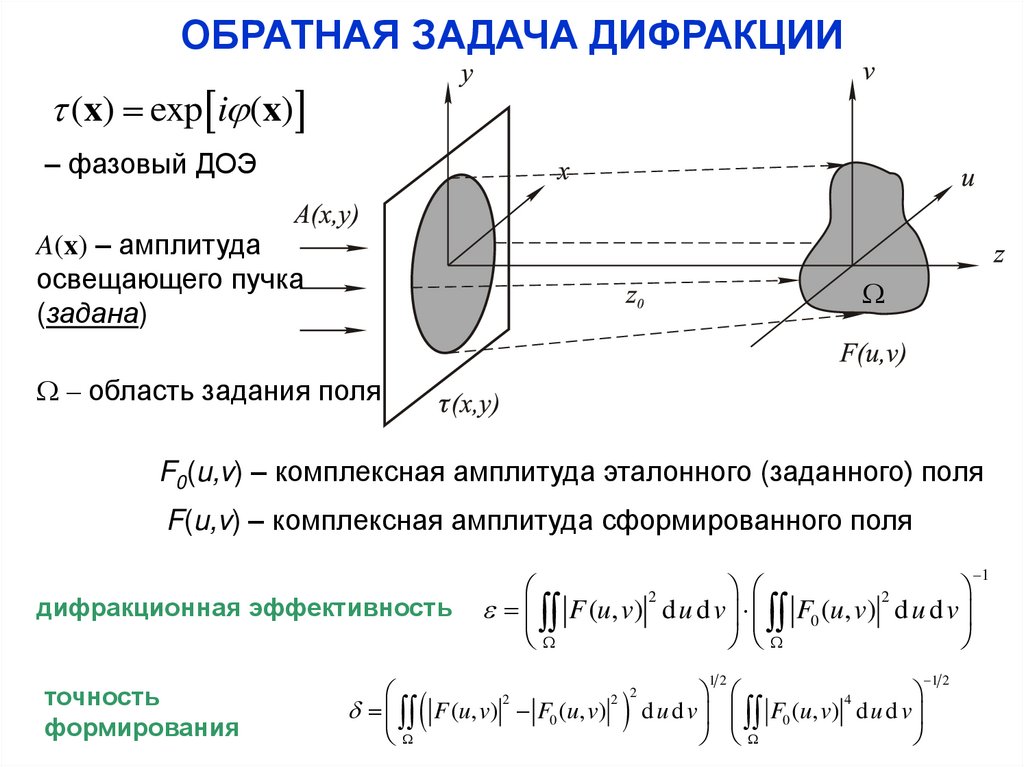
1. ОБРАТНАЯ ЗАДАЧА ДИФРАКЦИИ

(x) exp i (x)
– фазовый ДОЭ
A(x) – амплитуда
освещающего пучка
(задана)
– область задания поля
F0(u,v) – комплексная амплитуда эталонного (заданного) поля
F(u,v) – комплексная амплитуда сформированного поля
дифракционная эффективность
точность
формирования
2
2
12
2
2 2
4
F (u, v) F0 (u, v) d u d v F0 (u, v) d u d v
F (u, v) d u d v F0 (u, v) d u d v
1 2
1

2. ИТЕРАЦИОННЫЕ АЛГОРИТМЫ РАСЧЕТА ФАЗОВЫХ ДОЭ

Шаги расчета фазы ДОЭ (x) на k-ой итерации:
(0)(x) – случайная начальная оценка
1. Выполнение прямого
преобразования .
F ( k ) (u) A(x) exp i ( k ) (x)
Наложение условий DB на
2. формируемое
распределение
Fˆ ( k ) ( u) DB F ( k ) ( u)
Выполнение
3.
обратного
преобразования 1 .
( k ) ( x ) 1 Fˆ ( k ) ( u)
4. Наложение условий DA на ДОЭ
(чисто фазовый)
( k 1) (x) arg ( k ) (x)
5.
Переход к 1.
[ ] – оператор распространения

3. ИТЕРАЦИОННЫЕ АЛГОРИТМЫ РАСЧЕТА ФАЗОВЫХ ДОЭ

[ ] – преобразование
?
Фурье
Условие DA в объектной плоскости - ДОЭ д.б. чисто фазовым:
1
(k )
(k )
DA : ˆ( k ) (x) A(x) (x) (x) , x A ,
0, x A.
A(x) – заданный
освещающий пучок
A – форма апертуры ДОЭ
Условие DB в плоскости формирования - д.б. заданная интенсивность:
DB : Fˆ
I ( u) F ( k ) (u) F ( k ) ( u) , u ,
B
( u) 0
0, u B ,
1
(k )
I0(u) – заданная
интенсивность,
В – область задания
формируемого
распределения

4. ИТЕРАЦИОННЫЕ АЛГОРИТМЫ РАСЧЕТА ФАЗОВЫХ ДОЭ

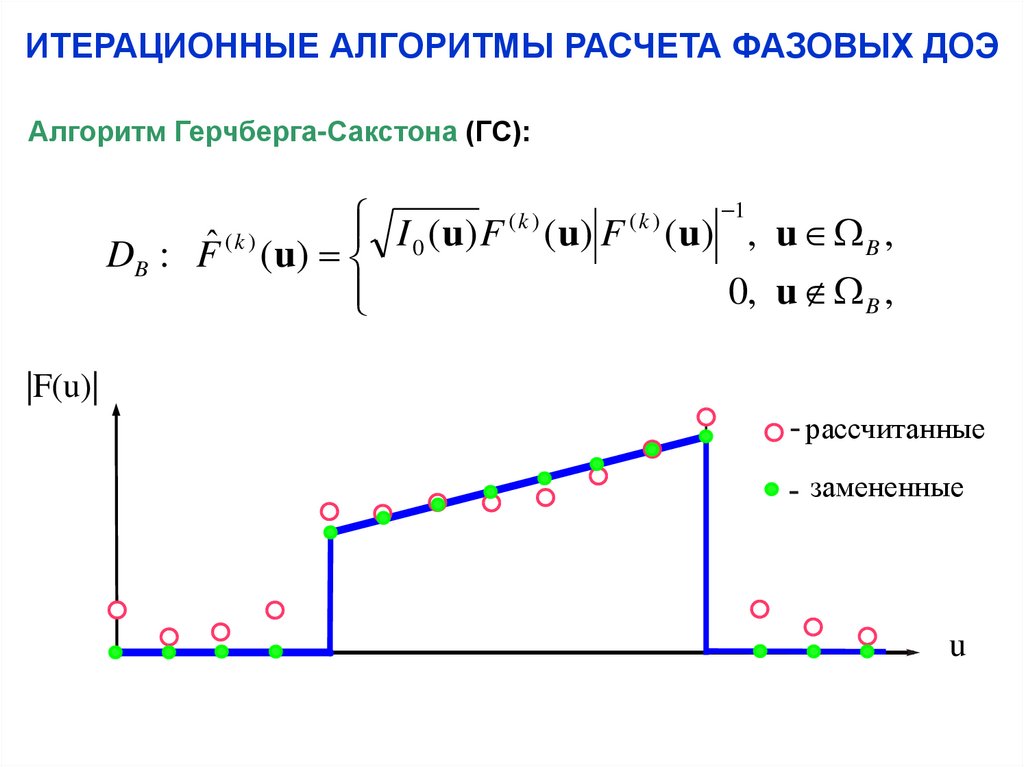
Алгоритм Герчберга-Сакстона (ГС):
1
(k )
(k )
I ( u) F ( u) F ( u) , u B ,
DB : Fˆ ( k ) (u) 0
0, u B ,
|F(u)|
рассчитанные
замененные
u

5. ИТЕРАЦИОННЫЕ АЛГОРИТМЫ РАСЧЕТА ФАЗОВЫХ ДОЭ

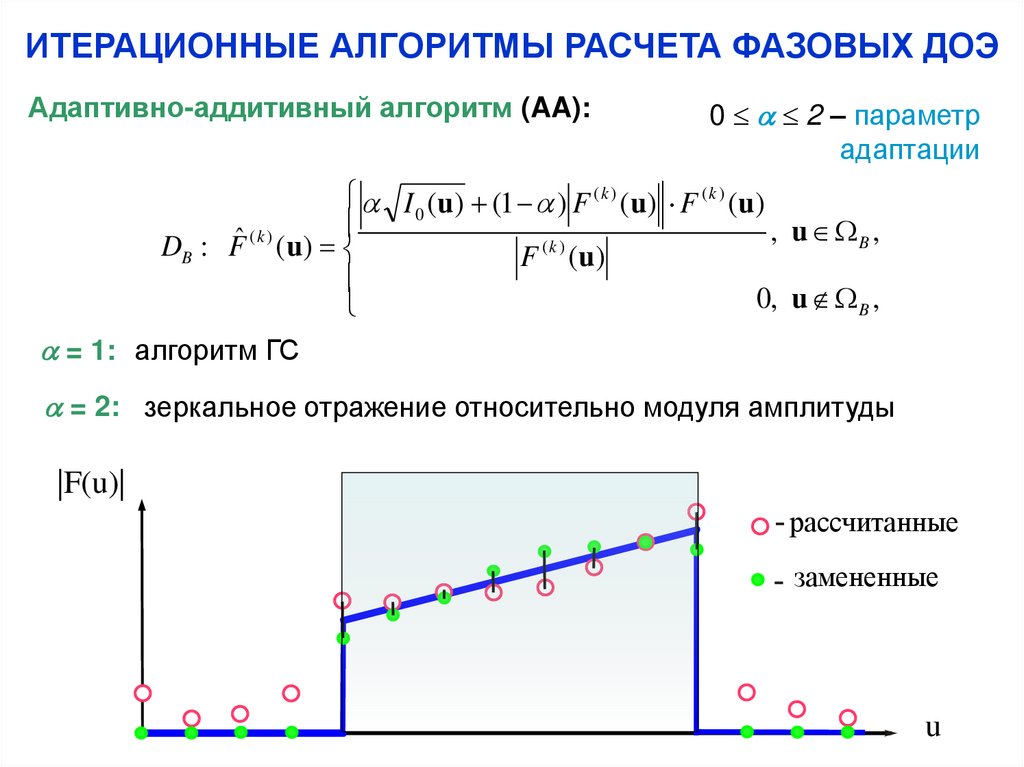
Адаптивно-аддитивный алгоритм (AA):
0 2 – параметр
адаптации
I 0 (u) (1 ) F ( k ) ( u) F ( k ) (u)
, u B ,
(k )
ˆ
(k )
DB : F ( u )
F ( u)
0, u B ,
= 1: алгоритм ГС
= 2: зеркальное отражение относительно модуля амплитуды
|F(u)|
рассчитанные
замененные
u

6. ИТЕРАЦИОННЫЕ АЛГОРИТМЫ РАСЧЕТА ФАЗОВЫХ ДОЭ

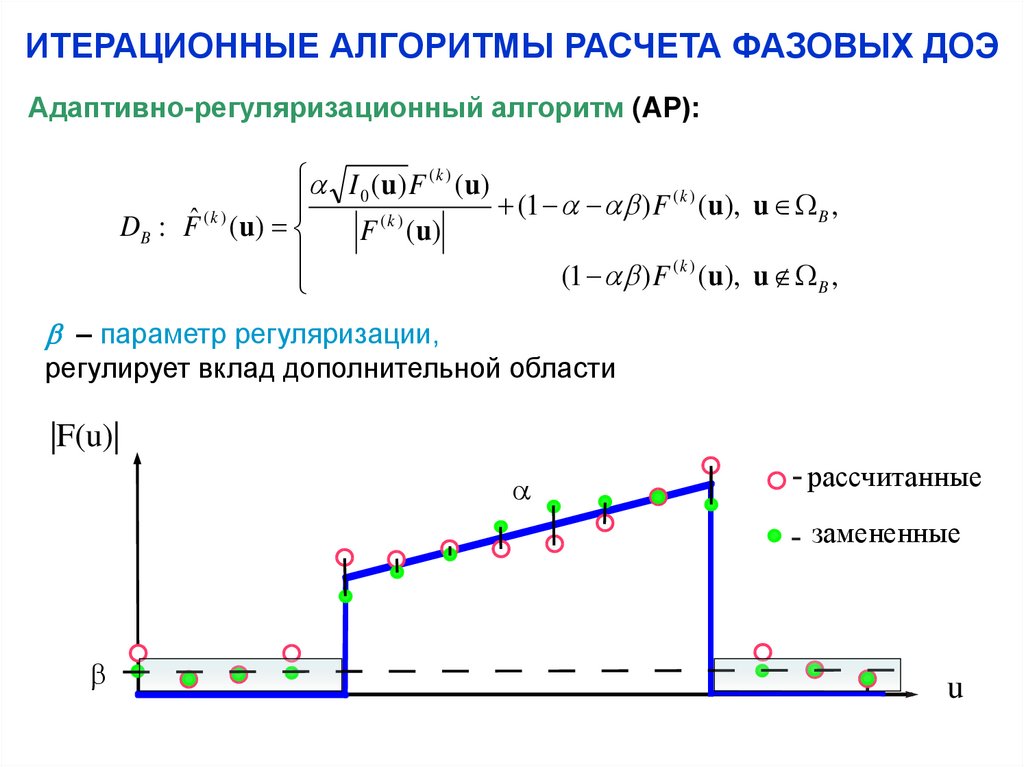
Адаптивно-регуляризационный алгоритм (AР):
I 0 ( u ) F ( k ) ( u )
(k )
(
1
)
F
( u), u B ,
(k )
(k )
ˆ
DB : F ( u )
F ( u)
(k )
(
1
)
F
( u), u B ,
– параметр регуляризации,
регулирует вклад дополнительной области
|F(u)|
рассчитанные
замененные
u

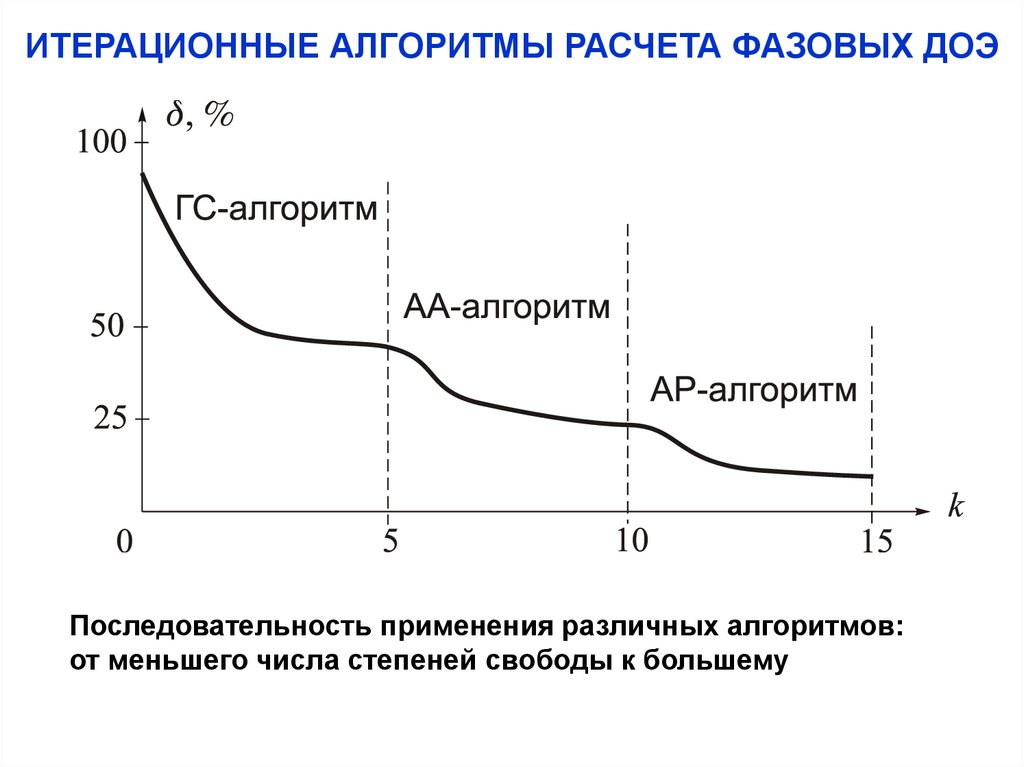
7. ИТЕРАЦИОННЫЕ АЛГОРИТМЫ РАСЧЕТА ФАЗОВЫХ ДОЭ

Последовательность применения различных алгоритмов:
от меньшего числа степеней свободы к большему