Берілістер

1.

Дәріс 10
БЕРІЛІСТЕР
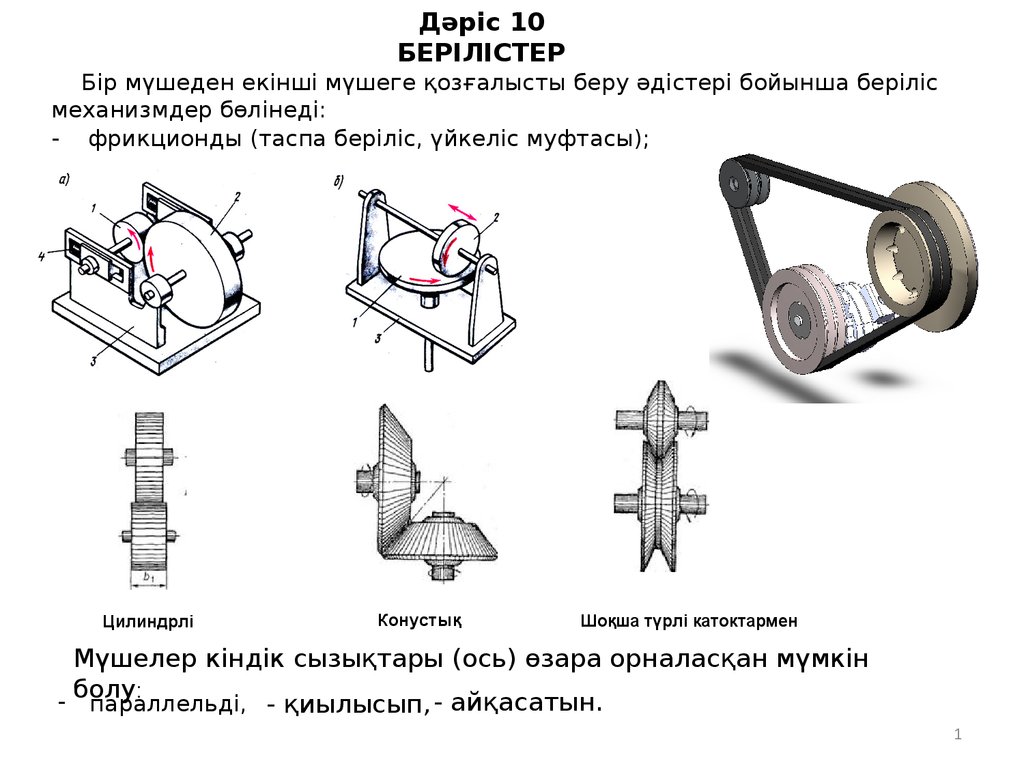
Бір мүшеден екінші мүшеге қозғалысты беру әдістері бойынша беріліс
механизмдер бөлінеді:
- фрикционды (таспа беріліс, үйкеліс муфтасы);
Цилиндрлі
Конустық
Шоқша түрлі катоктармен
Мүшелер кіндік сызықтары (ось) өзара орналасқан мүмкін
- болу:
параллельді, - қиылысып, - айқасатын.
1

2.

ілініс (шынжырлы, тісті).
Қарапайым механизм екі қозғалмалы және бір қозғалмайтын
мүшелерден тұрады, оны саты деп атайды.
2

3.

Беріліс механизмдегі негізгі кинематикалық қатынастар
– беріліс қатынасы,
U ij
n1 1 мұндағы: 1, n1
U12
айналу
n2 2
- сәйкес өлшенетін мүшелердің
жиілігі, айн./мин. және с-1.
Кіндік сызықтары параллельді механизмдер
U 12 0,
1
3
r 1
1
1
Р12
2
U 34 0
Р34
r 3
3
3
2
r 4
r 2
2
U12
1 r 2
2 r 1
4
V p 1 V p 2 , 1 r 1 2 r 2
4
U 34
4
3 r 4
4 r 3
3

4.

Мүше кіндік сызықтары қиылысып орналасқан
механизмдер
1 2 90o
1
U12
мұндағы:
1 Sin 2
2 Sin 1
2
1және 2конусты құраушы бұрыштар
O
Мүшелер кіндік сызықтары айқасатын механизмдер
Бұрамдықты беріліс
4

5.

Тісті берілістер
цилиндрлі, мүшелер кіндік сызықтары параллель орналасқан;
-
конустық, мүшелер кіндік сызықтары қиылысатын;
5

6.

гиперболоидты, мүшелер кіндік сызықтары айқас орналасқан.
6

7.

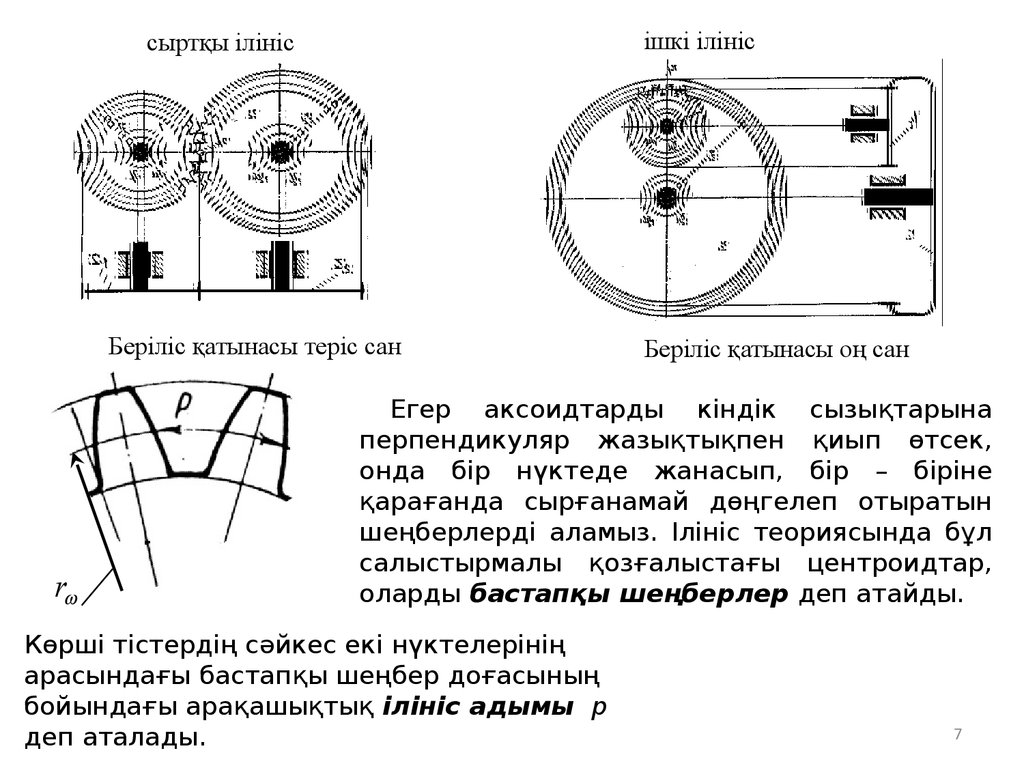
ішкі ілініс
сыртқы ілініс
Беріліс қатынасы теріс сан
r
Беріліс қатынасы оң сан
Егер аксоидтарды кіндік сызықтарына
перпендикуляр жазықтықпен қиып өтсек,
онда бір нүктеде жанасып, бір – біріне
қарағанда сырғанамай дөңгелеп отыратын
шеңберлерді аламыз. Ілініс теориясында бұл
салыстырмалы қозғалыстағы центроидтар,
оларды бастапқы шеңберлер деп атайды.
Көрші тістердің сәйкес екі нүктелерінің
арасындағы бастапқы шеңбер доғасының
бойындағы арақашықтық ілініс адымы р
деп аталады.
7

8.

Екі тісті доңғалақтар бірге жұмыс істеуінің шарты:
p1 p2
Бастапқы шеңбердің ұзындығы: d
2 r pz,
мұндағы:
d
p
z
z
d
- бастапқы шеңбердің диаметрі
- тістер саны.
р
m - модуль деп атаймыз, мм
Сондықтан, екі дөңгелектің ілінісі мұмкін
d mz
егер,
m1 = m2
Модулі рационалды мәндер қатардағы бірінің мәнімен сәйкес
келген шеңберді бөлгіш шеңбер деп атайды.
Осымен, беріліс қатынасын анықтайтын тағы бір өрнек
r
шықты:
d
z
U12 2 2 2
r 1
d1
z1
8

9.

Көп сатылы беріліс
да 2 және 2', 3 және 3', 4 және 4', 5 және 5' дөңгелектері өзара біліктермен
лғасқан. Олар бірімен – бірі қатаң байланыста, яғни бір мүше, сондықтан
1
2 2' , 3 3' ,
4
4 4' , 5 5'
Жеке сатылардың беріліс
қатынастары:
'
1 U 2 ,
U12 , 2'3
3
2
4'
U 4 '5
,
5
U 5 '6
U12 U 2 '3 U 3' 4 U 4 '5 U 5'6
6
U 3' 4
2/
2
4
/
3'
,
4
5'
6
5
3
3/
/
5
1 2' 3' 4' 5'
2 3 4 5 6
U12 U 2'3 U 3'4 U 4'5 U 5'6
1
( 1) 4 Көп сатылы механизмнің беріліс
6
қатынасы :
k
U 12 U 2'3 U 3'4 U 4'5 U 5'6 1 U 16
4
U1n U12 U 2'3 U 3'4 U n 1 n 1
1
n
( 1) k
мүнда k – сыртқы ілініс сатылар
саны
9