Проект «Удивительный мир чисел»

1.

ПРОЕКТ
«УДИВИТЕЛЬНЫЙ МИР
ЧИСЕЛ»

2.

ПИФАГОР
Числа
древними греками,
а вместе с ними Пифагором
и пифагорейцами мыслились
зримо, в виде камешков,
разложенных на песке или на счетной доске –
абаке.
Пифагорейские числа в современной
терминологии - это натуральные числа.
Числа-камешки раскладывались в виде
правильных геометрических фигур, эти
фигуры классифицировались. Так возникли
числа, сегодня именуемые фигурными.

3.

ЛИНЕЙНЫЕ ЧИСЛА
Линейные
числа - самые простые числа,
которые делятся только на единицу и
на самих себя и вследствие этого могут
быть изображены в виде линии,
составленной из последовательно
расположенных точек. Примером
линейного числа является - число 5

4.

РЕШЕТО ЭРАТОСФЕНА
Более двух тысяч лет назад в Греции знаменитый
математик Эратосфен придумал очень остроумный
способ выискивать простые числа. Он предложил для
этого применять особое решето, сквозь которое все
ненужные числа будут просеиваться, а все нужные –
простые
оставаться.
Чудесное
решето
назвали решетом Эратосфена.

5.

ПЛОСКИЕ ЧИСЛА. ТЕЛЕСНЫЕ ЧИСЛА.
Плоские
числа – числа, представимые в виде
произведения двух сомножителей, (или
составные): 4; 6; 8; 10; . . .
(число 6)
(число 10)
Эти числа можно расположить в две линии.
Телесные числа – числа, представимые в виде
произведения трёх сомножителей: 8; 12; 16;
18; . . .

6.

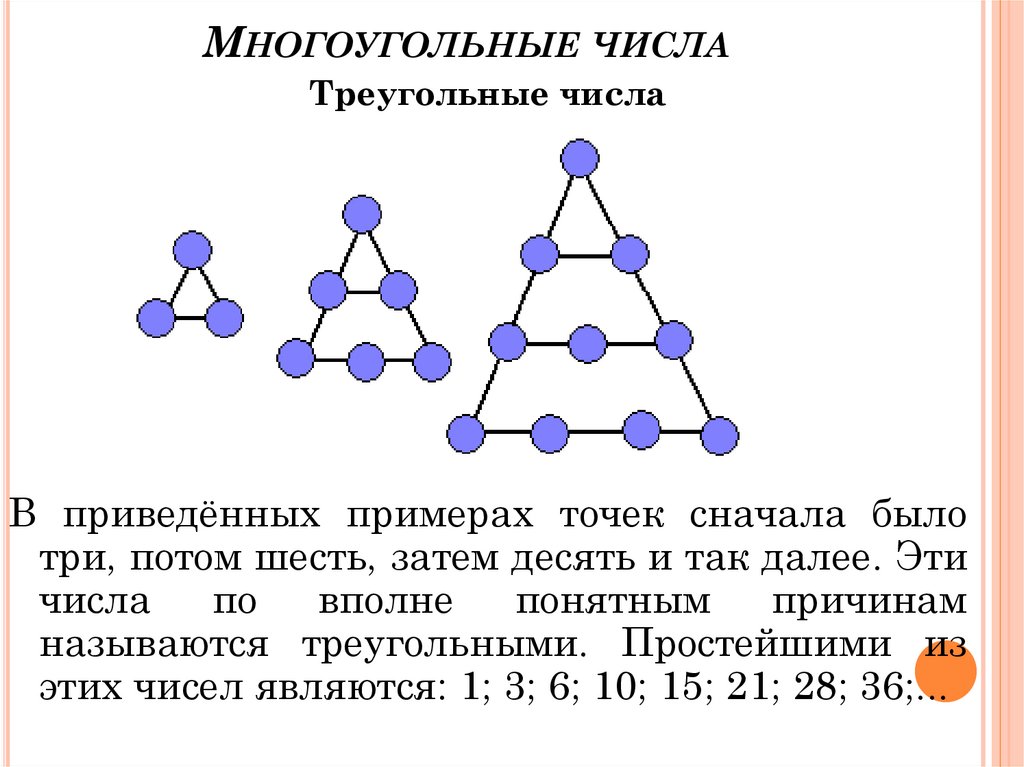
МНОГОУГОЛЬНЫЕ ЧИСЛА
Треугольные числа
В приведённых примерах точек сначала было
три, потом шесть, затем десять и так далее. Эти
числа
по
вполне
понятным
причинам
называются треугольными. Простейшими из
этих чисел являются: 1; 3; 6; 10; 15; 21; 28; 36;...

7.

1
3=1+2
6=1+2+3
10=1+2+3+4
15=1+2+3+4+5
21=1+2+3+4+5+6 и т.д.
Любое треугольное число
представить в виде ,
можно
где n – порядковый номер числа.

8.

КВАДРАТНЫЕ ЧИСЛА
Нарисованные точки образуют правильную
геометрическую фигуру – квадрат. Квадратными
числами называются числа ряда: 1; 4; 9; 16; 25; 36; 49;
64; 81; 100; . .
1
1=1х1
4
4=2х2
9
16
9=3х3
25
16=4х4….

9.

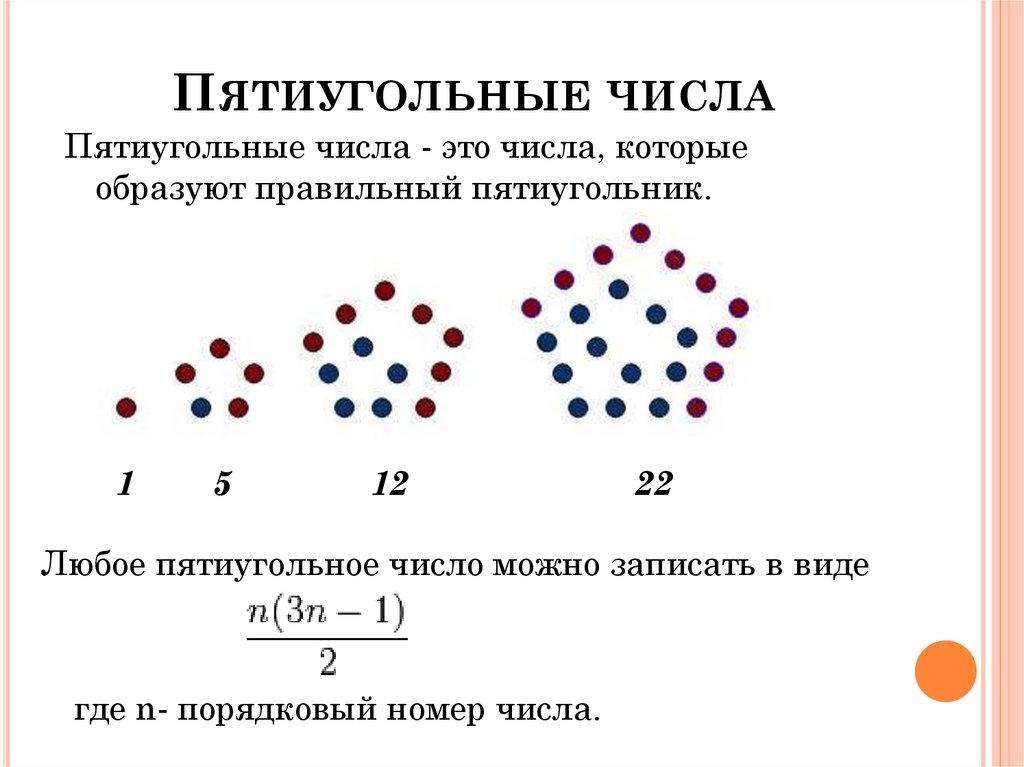
ПЯТИУГОЛЬНЫЕ ЧИСЛА
Пятиугольные числа - это числа, которые
образуют правильный пятиугольник.
1
5
12
22
Любое пятиугольное число можно записать в виде
где n- порядковый номер числа.

10.

СОВЕРШЕННЫЕ ЧИСЛА
Совершенное число — натуральное число, равное сумме
всех своих собственных делителей (т. е. всех положительных
делителей, отличных от самого числа). По мере того как
натуральные числа возрастают, совершенные числа
встречаются всё реже.
6 — шесть. Делители числа 6 - 1; 2; 3 – собственные
делители.
6=1+2+3
28 — двадцать восемь. Делители числа 28 - 1; 2; 4; 7; 14 собственные делители.
28=1+2+4+7+14
496 — четыреста девяносто шесть.
Четвёртое совершенное число — 8128,
Пятое — 33 550 336,
Шестое — 8 589 869 056,
Седьмое — 137 438 691 328 . . .
В диапазоне от 1 до 100 всего 2 числа- 6 и 28

11.

12.

28 сентября число 28 решило пригласить в
гости всех своих делителей, меньших, чем
оно само. Первой прибежала единица, за ней
двойка, за ней 4; 7; 14. Когда все гости
собрались, число 28 увидело, что их
немного. Оно огорчилось и предложило,
чтобы каждый из гостей привел ещё и своих
делителей. (Сколько придет новых гостей?).
Единица объяснила числу 28, что новые
гости не придут.

13.

Чтобы утешить число 28 , его гости соединились
знаком "+". И, о чудо, сумма оказалась равной самому
числу 28! Единица сказала, что всякое число, которое
равно
сумме
своих
меньших
делителей,
называется совершенным. Число обрадовалось и
спросило, какие числа есть ещё совершенные.
Всезнающая единица ответила, что совершенных
чисел очень мало: среди чисел до миллиона их всего
четыре: 6, 28, 496 и число 8128. К сожалению,
совершенных чисел всего двадцать четыре: 6, 28,
496,8128, 130 816… Дальше они растут всё быстрее
и быстрее, а вычислять их всё сложнее и сложнее.
Может быть вам доведётся найти новое совершенное
число.

14.

ДРУЖЕСТВЕННЫЕ ЧИСЛА
Это пара чисел, обладающих таким свойством: сумма
собственных делителей (не считая самого числа) первого из
них равна второму числу, а сумма собственных делителей
второго числа равна первому числу. Они открыты
древнегреческими учеными - последователями Пифагора.
Недаром знаменитый греческий математик Пифагор
сказал: «Друг – это второе я!» – и при этом сослался на
числа 220 и 284. Они замечательны тем, что каждое из них
равно сумме младших делителей другого числа. Какие
делители у числа 284?
1, 2, 4, 71, 142.
А у числа 220 делители:
1, 2, 4, 5, 10, 11, 20, 22, 44, 55, 110.
Попробуем сложить делители каждого числа:
1 + 2 + 4 + 71 + 142 = 220,
1 + 2 + 4 + 5 + 10 + 11 + 20 + 22 + 44 + 55 + 110 = 284.

15.

16.

И
З
В
Найд Б
И
и
24 О
слова С
Т
Д
И
А
М
Е
О
Е
Е
С
С
К
О
Ь
А
К
С
И
Т
Р
И
Д
Е
К
Р
Н
О
П
Р
Е
О
Р
П
Н
Е
Р
Т
У
Ж
Е
Л
Е
Д
М
А
С
А
К
И
С
А
И
Н
Г
И
П
О
Т
А
Т
Е
Л
У
Ч
Е
М
Е
Д
И
А
Е
Н
Ь
Л
П
В
О
Т
Р
А
В
А
Н
Н
А
А
Т
Е
Ы
С
А
И
Д
Е
Т
З
У
Я
Н
А
Р
Г
Е
С
У
Т
К
Р
А
К
И
Е
П
Т
К
С
Р
О
Н
А
Г
Е
О
Д
Н
Д
А
Р
Е
К
П
С
И
Р
О
О
Р
К
И
Я
А
Щ
У
О
Р
Т
Е
М
Я
Л
У
К
Р
О
Р
Н
И
Е
Р
Т
К
Р
О
Р
А
У
С
А
Я
О
О
И
Я
О
Т
Е
Е
М
Г
Ь
С
С
Т
Т
Р
Е
З

17.

Вы сумеете угадать день рождения
даже незнакомого вам человека,
если получите у него ответы на
ваши вопросы.
Угадывание дня
рождения

18.

Допустим он родился 7 октября.
1.) Запишите день своего рождения, т.е. число (например 7)
2.) умножьте его на 2 (7 * 2 = 14)
3.) к полученному числу припишите 0 (140)
4.) к результату прибавьте 73 (140 + 73 = 213)
5.) полученное число умножьте на 5 (213 * 5 = 1065)
6.) прибавьте к полученному числу номер месяца, в котором
вы родились (1065 + 10 = 1075)
7.) назовите свой ответ, а я назову день и месяц вашего
рождения …
Для получения ответа нужно из полученного результата
вычесть 365
(1075 – 365 = 710). В полученном числе первые две цифры или
одна, если число трехзначное, - день рождения, другие две номер месяца
У нас получилось: 710
7 - день рождения
10 - номер месяца
Результат: 7 октября

19.

ЗАДАЧИ - ШУТКИ
Летели утки: одна впереди и две позади, одна
позади и две впереди, одна между двумя и три в
ряд. Сколько всего летело уток?
2. Сколько концов у палки? У двух палок? У двух
с половиной?
От стола отпилили угол. Сколько углов
осталось?
Что это может быть: две головы, две руки и
шесть ног, а при ходьбе только четыре?

20.

ЗАДАЧИ В СТИХАХ
По тропинке вдоль кустов
шло
Одиннадцать хвостов
Сосчитать я также смог,
Что шагало тридцать ног,
А теперь вопрос таков:
Сколько было петухов?
И узнать я был бы рад,
Сколько было поросят?
Акробат и собачонка
Весят два пустых бочонка.
Шустрый пес без акробата
Весит два мотка шпагата.
А с одним мотком ягненок
Весит, видите, бочонок.
Сколько весит акробат
В пересчете на ягнят?
(33 : 3 + 3 – 3 =11)

21.

ПРОВЕРЬ СЕБЯ!
(7 петухов, 4 поросенка)
(акробат весит как два ягненка)