356.90K

Category:

informatics

Нечеткие нейронные сети

2.

Нечеткие модели вывода
Фазификация
Вычисление посылки
Импликация
Агрегация
Дефазификация

3.

Нейронные модели вывода
Предобработка
Обучение
Подать образец
Изменить W
Интерпретация

4.

Нейро-нечеткие модели
Нейронная модель нечеткого вывода
Нечеткие нейроны

5.

фазификация
(x)
Нейроны RBF
C
C
-
(x)
Z
X
+
Exp(-Z2/(2 ))
X

6.

Нейроны И, ИЛИ
И – нейрон (T-норма (+), кТ-норма (*) )
ИЛИ – нейрон (kT-норма (+), Т-норма (*) )
Производные Т-нормы и кТ-нормы
y 1, y xi
xi 0, y xi

7.

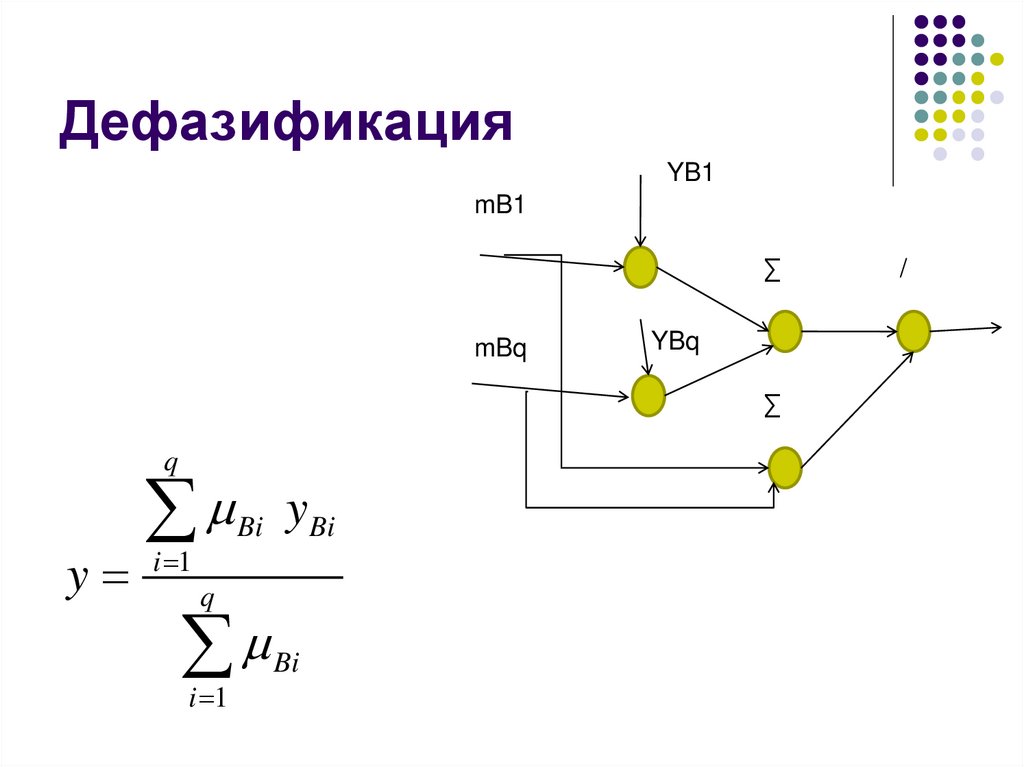
Дефазификация
YB1
mB1
∑
mBq
YBq
∑
q
y
i 1
Bi
yBi
q
i 1
Bi
/

9.

Сеть Такаги-Сугено-Канга
Слой 1
слой 2/слой 3/слой 4/слой 5

Функции слоев
1. Первый слой выполняет фазификацию каждой переменной. Это
параметрический слой с параметрами , подлежащими адаптации в
процессе обучения.
2. Второй слой выполняет агрегирование отдельных переменных,
определяя результирующее значение коэффициента
принадлежности для вектора (непараметрический слой).
3. Третий слой - генератор функции TSK, рассчитывает значения. В
этом слое также производится умножение на , сформированные в
предыдущем слое. Здесь адаптации подлежат веса ,
определяющие функцию следствия модели TSK.
4. Четвертый слой составляют два нейрона-сумматора, один из
которых рассчитывает взвешенную сумму сигналов , а второй сумму весов (непараметрический слой).
5. Пятый слой из одного нейрона - это нормализующий слой, в
котором выходной сигнал сети агрегируется.

11.

Обучение
первом этапе при фиксации определенных
значений параметров функции
принадлежности
При Р обучающих выборках (Х(l),d(l)),
l=1,2,…, P

12.

Обучение
- псевдоинверсия

13.

Обучение
второй этап (линейные параметры фиксированы) рассчитываются
фактические выходные сигналы
y=W*p
вектор ошибки
E=y-d

14.

Обучение

15.

Обучение
После уточнения нелинейных параметров
вновь запускается процесс адаптации
линейных параметров TSK (первый этап)
и нелинейных параметров (второй этап).
Цикл повторяется вплоть до стабилизации
всех параметров процесса.

16.

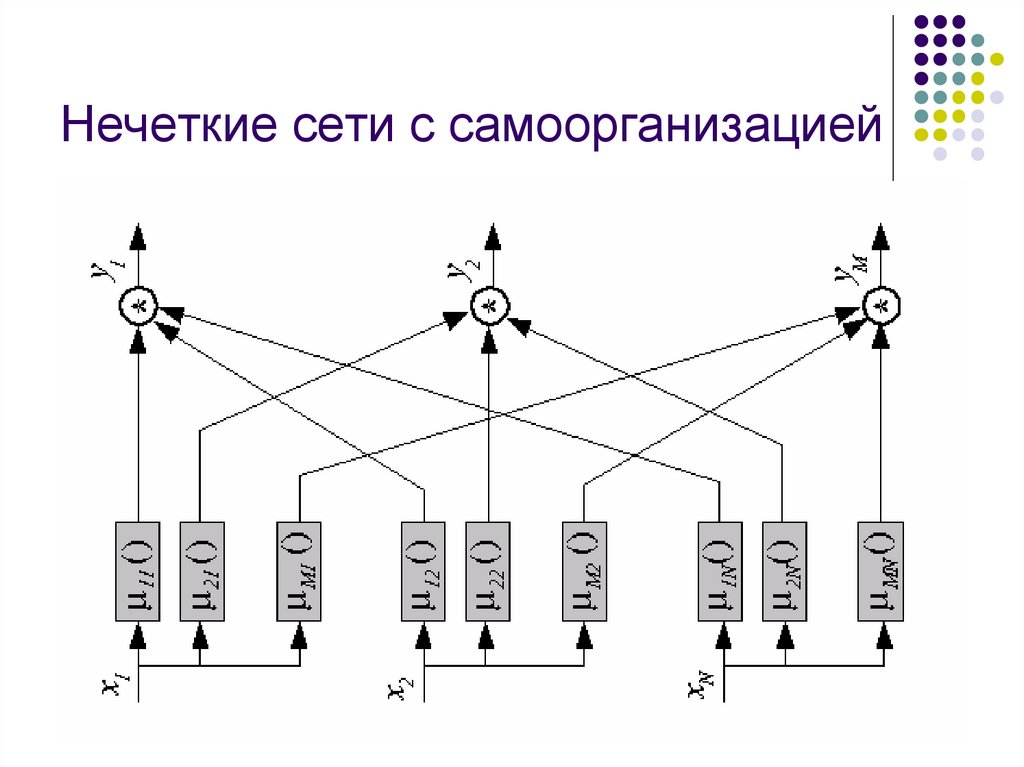
Нечеткие сети с самоорганизацией

17.

архитектура
первый слой обобщенная функция Гауcса
:
ij(xj)=1/(1+((xj-cij)/sij)2*bij).
второй слой характеризуется
центром Ci=[u1i, u2i, ..., uNi, ]T.

18.

Алгоритм нечеткой
самоорганизации К-means
подаваемый на вход очередной
обучающий вектор Xk принадлежит
различным кластерам (представленным
своими центрами Ci, i=1, 2, ..., M) в
степени uki, 0<uki<1, при соблюдении
условия
(uki)=1, i=1:M
uki тем больше, чем ближе Xk к Ci

19.

Обучение
min(E)
E=
u
ki
m
X k -Ci
2
i=1,M k=1,p
,
Ci= ((uki)m*Xk / (uki)m,
k=1:p
uki=1/ (((dki)2/(dkl)2))1/(m-1)),
l=1:M
dki=|Xk-Ci|2 - эвклидово расстояние между
X k и C i.

20.

Обучение
Выполнить случайный выбор коэффициентов uki
из диапазона [0,1] при соблюдении условия
(uki)=1, i=1:M.
2. Вычислить все M центров Ci .
3. Рассчитать значение погрешности E. Если это
значение меньше установленного порога или
незначительно изменилось относительно
предыдущей итерации, то закончить вычисления.
Иначе перейти к п. 4.
4. Рассчитать новые значения uki и перейти к п. 2

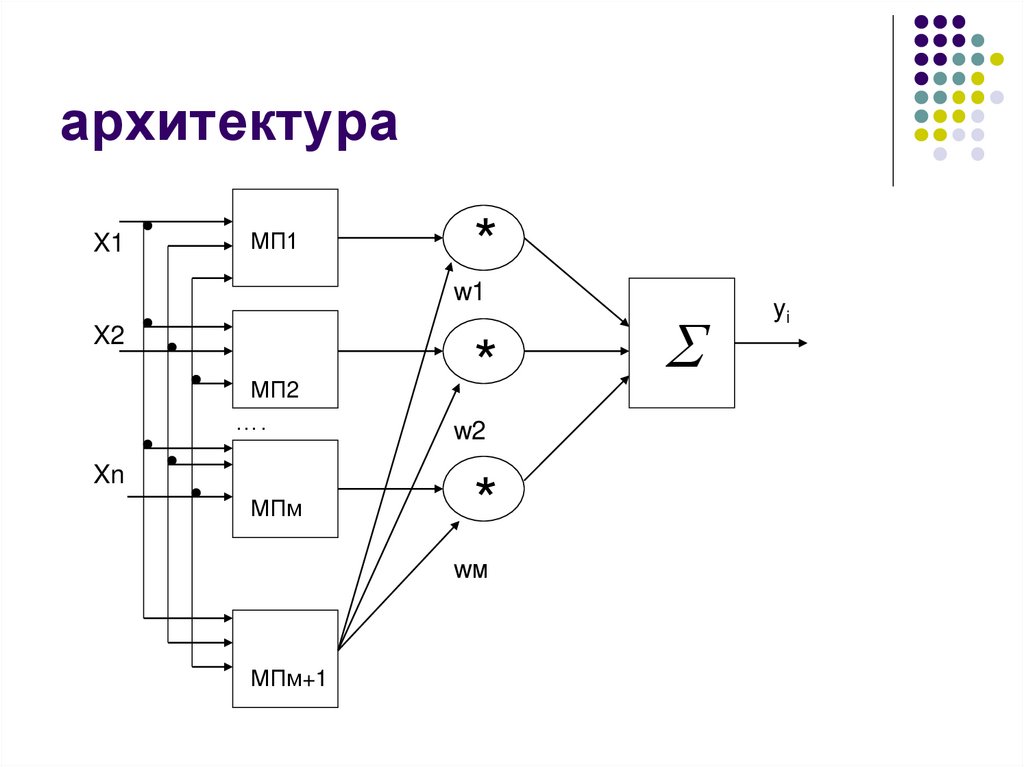
21.

архитектура
X1
МП1
*
w1
X2
МП2
….
Xn
МПм
*
w2
*
wм
МПм+1
yi

22.

обучение
Шаг 1.
Удалить неинформативные переменные
Обучить МПi – отдельно.
Обучить все МПi вместе.
Модиифцировать веса и проверить
ошибку сети

23.

обучение
Шаг 2.
Эвристически определяем количество
кластеров Х.
МП учить на выделение кластеров Х.
Если Хк принадлежит Aj, то wj(Xk)=1-yМП
иначе wj=0.

24.

обучение
Шаг 3.
Обучить МПi – отдельно по ВР
Шаг 4.
Исключение слабых МПi.
Получим схему
Если X=A1, то МП1(Х1, Х2, …, Хn)
Если X=A2, то МП2(Х1, Х2, …, Хn)
….
Если X=Am, то МПm(Х1, Х2, …, Хn)

25.

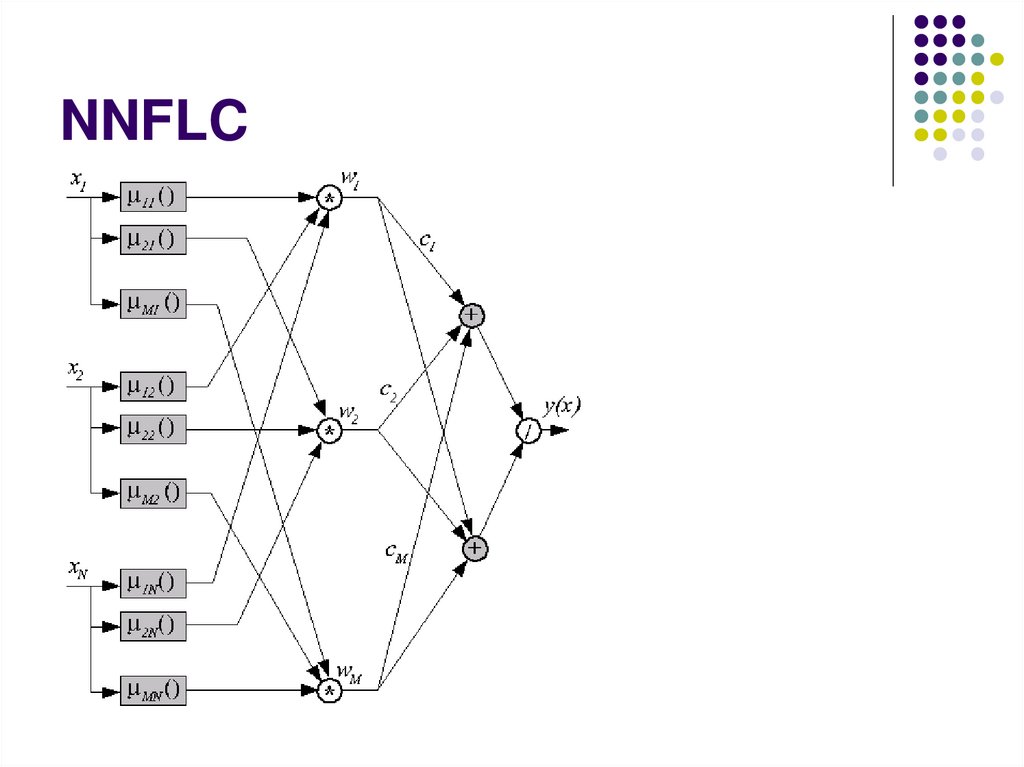
NNFLC

26.

NNDFR
Neural Network Driven Fuzzy Reasoning
Нейронная сеть для нечетких
рассуждений
Первый слой – NN – многослойные
перцептроны (правила «ЕСЛИ - ТО»)
Второй слой - комбинирование правил

27.

GARIC
Generalized Approximate Reasoning Based
on Intelligent Control
Состоит из 2-х связанных нечетких сетей
(управления и оценки)
Реализует вывод Цукамото
Yj(t+1)=f( aij*xi)
f(s)=1/(1+e-s)

28.

архитектура
НС оценки
Линейный
Многослойный
персептрон
r
=r-rp
Х
НС управления
у
V
объект
У’

29.

Сеть управления
x1
Softmin
y
Softmin
defuzz
xn
Softmin
Softmin

30.

ANFIS
Adaptive Network based Fuzzy Inference
System
Вывод Сугено

31.

IF x1 is A1 .and. X2 is B1 THEN
y1=c11*x1+c12*x2
IF x1 is A1 .and. X2 is B2 THEN
y2=c21*x1+c22*x2
Выход ANFIS
Y=(w1*y1+w2*y2)/(w1+w2)

32.

<w1>
ANFIS модель
c11
µA1(x1)
х1
µA2(x1)
<w1>y1’
w1
.and.
.and.
y1
c12
y
х2
µB1(x1)
.and.
.and.
y1
µB2(x1)
<w2>y2’
w2
<w2>
слой 1
слой 2
слой 3
слой 4
слой 5

33.

Реализация ANFIS
x = (0:0.1:10)';
y = sin(2*x)./exp(x/5);
trnData = [x y]; //данные
numMFs = 5; //число входов
mfType = 'gbellmf'; // тип функций принадлежности
epoch_n = 20;
//число эпох тренировки
% генерация сети
in_fismat = genfis(trnData,numMFs,mfType);
% обучение сети
out_fismat = anfis(trnData,in_fismat,20);
plot(x,y,x,evalfis(x,out_fismat));
legend('Training Data','ANFIS Output');

34.

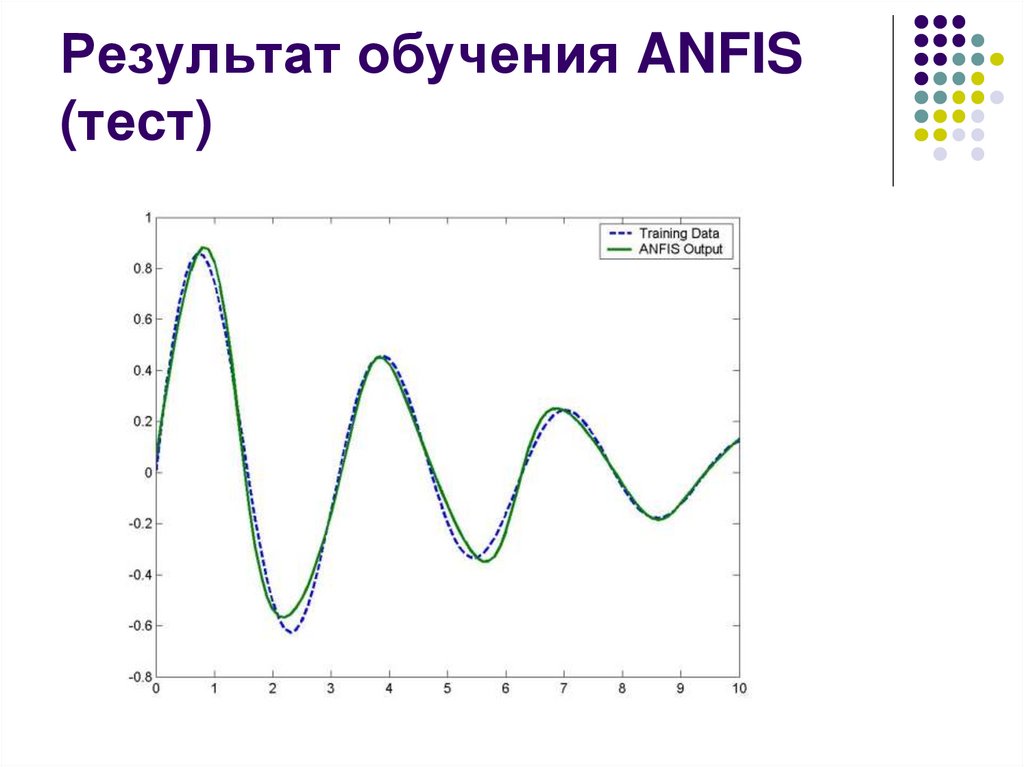
Результат обучения ANFIS
(тест)

35.

Результат обучения ANFIS
(сеть)
out_fismat =
name: 'anfis'
type: 'sugeno'
andMethod: 'prod'
orMethod: 'max'
defuzzMethod: 'wtaver'
impMethod: 'prod'
aggMethod: 'max'
input: [1x1 struct]
output: [1x1 struct]
rule: [1x5 struct]

36.

Результат обучения ANFIS
(входы)
out_fismat.input(1).mf(1)
[x,mf] = plotmf(out_fismat,'input',1);
subplot(2,1,1), plot(x,mf);

37.

Результат обучения ANFIS
(вход 1 )
name: 'in1mf1'
type: 'gbellmf'
params: [1.3970 2.0053 0.1369]

38.

Описание правила
out_fismat.rule(1)
out_fismat.rule(2)
antecedent: 1 %посылка
consequent: 1 %следствие
weight: 1
%значимость
connection: 1 %число связей
antecedent: 2
consequent: 2
weight: 1
connection: 1

39.

5 входов
x = (0:0.1:10)';
y = sin(20*x)./exp(x/5);
trnData = [x y]; %данные
numMFs = 5; %число входов
epoch_n = 20;

40.

50 входов
x = (0:0.01:10)';
y = sin(20*x)./exp(x/5);
trnData = [x y]; %данные
numMFs = 50; %число входов
mfType = 'gbellmf'; % тип
функций принадлежности
epoch_n = 20;

41.

x = (0:0.1:10)';
y = sin(20*x)./exp(x/5);
trnData = [x y]; %данные
numMFs = 50; %число входов
epoch_n = 20;

42.

Темы рефератов
Применение нечетких нейронных сетей в
регуляторах.
Применение нечетких нейронных сетей в
распознавании образов.
Методы формирования нечетких сетей на основе
вывода Мамдани.
Методы формирования нечетких нейронных
сетей на основе вывода Сугено
Нечеткие нейроны: модели и их реализация.

43.

Литература
Интернет-Университет информационных Технологий.
http://www.INTUIT.ru Нейрокомпьютерные системы. Лекция 15:
Нечеткие и гибридные нейронные сети
Комарцова Л.Г. Максимов А.В. Нейрокомпьютеры. 2004

English Русский Rules