Прикладная универсальная алгебра

1.

Прикладная
универсальная алгебра

2.

Универсальная алгебра занимается изучением
общих свойств множеств с заданными на них
функциями и отношениями, которые называются
алгебраические системы.
Множеств с заданными на них функциями
называются алгебрами.
Множества с заданными на них отношениями
называются релятивами или моделями.
Основана в 30-х годах ХХ века Г.Биркгофом.

3.

Содержание дисциплины
1. Введение в
отношений.
универсальную
алгебру.
Алгебра
2. Упорядоченные множества и решетки.
3. Универсальные алгебры и основные конструкции.
4. Теория моделей.
5. Теория конечных автоматов.
6. Полугруппы, автоматы и языки.
7. Комбинаторная теория групп.
8. Комбинаторная теория полей.
9. Алгебраическое распознавание языков.

4.

Алгебра отношений

5.

Способы задания
бинарных отношений

6.

Бинарные
отношения
как
множества задаются с помощью 2-местных
предикатов
по формуле:

7.

1. Графом бинарного отношения на
множестве A {a1 ,...,an } называется плоская
фигура, которая состоит из n выделенных точек,
a1 ,..., a n
изображающих
элементы
и
называющихся вершинами графа, и у которой
вершины ai , a j , удовлетворяющие условию
(ai , a j ) , соединяются стрелкой, направленной
от a i к a j и называемой дугой графа.

8.

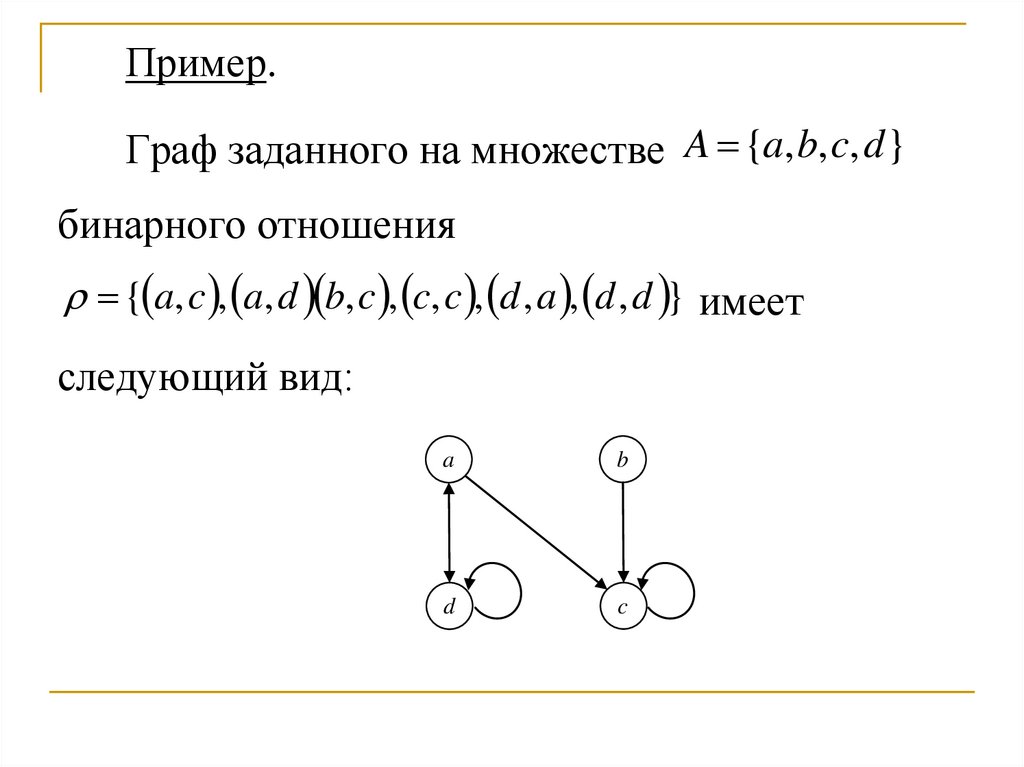
Пример.
Граф заданного на множестве A {a, b, c, d }
бинарного отношения
{ a, c , a, d b, c , c, c , d , a , d , d } имеет
следующий вид:
a
b
d
c

9.

2. Матрицей бинарного отношения между
элементами множеств A {a1 ,..., am } и B {b1 ,...,bn }
M ( ) ,
называется прямоугольная таблица
состоящая из m строк и n столбцов, в которой на
пересечении i-ой строки и j-го столбца стоит
[ M ( )]ij
элемент
из
множества
{0,1},
определяемый по правилу:
если (ai , b j ) ,
1,
[ M ( )]ij
0, в противном случае.

10.

Пример.
Матрица
заданного
A {a, b, c, d }
на
бинарного
множестве
отношения
{ a, c , a, d b, c , c, c , d , a , d , d }
следующий вид:
a
M ( ) b
c
d
a b
0 0
0 0
0 0
1 0
c d
1 1
1 0
1 0 .
0 1
имеет

11.

Свойства матриц бинарных отношений:
1) [M ( )]ij [M ( )]ij для всех
1 i m, 1 j n ;
2) элементы M ( ) вычисляются
[ M ( )]ij [ M ( )]ij [ M ( )]ij ;
3) элементы M ( ) вычисляются
[ M ( )]ij max{[ M ( )]ij , [ M ( )]ij } ;
4) если A B и B C для множества
C {c1 ,...,c p } , то элементы M ( ) вычисляются
[ M ( )]ij max {[ M ( )]ik [ M ( )]kj} .
1 k n

12.

Примеры.
1. Пусть A – множество студентов, сдающих
экзамены
( A A )
по
-
алгебре
бинарное
и
геометрии,
отношение
A A
сравнения
успеваемости студентов по алгебре (геометрии).
Отношения , , - транзитивны, но отношение
транзитивным может не быть.

13.

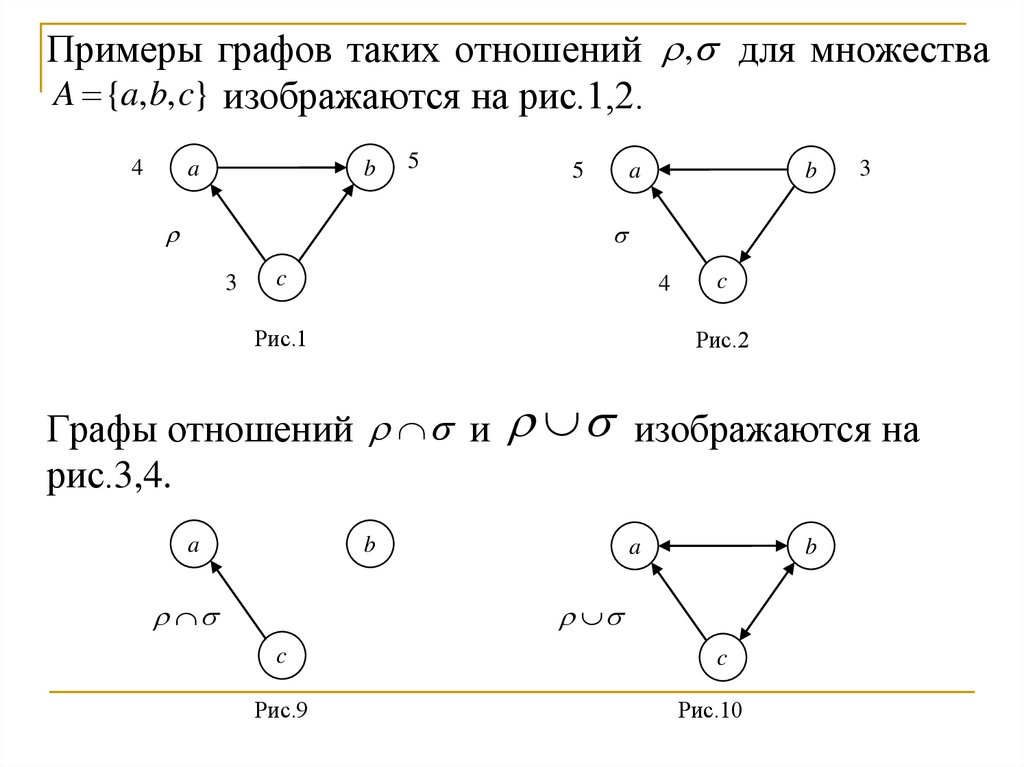
Примеры графов таких отношений , для множества
A {a, b, c} изображаются на рис.1,2.
4
a
b
5
5
a
b
3
3
c
4
Рис.1
Рис.2
Графы отношений и
рис.3,4.
a
b
c
изображаются на
a
b
c
Рис.9
c
Рис.10

14.

Очевидно, что данные бинарные отношения
представляются матрицами:
0 1 0
0 0 0
M ( ) 0 0 0 , M ( ) 1 0 1 ,
1 1 0
1 0 0
0 0 0
0 1 0
M ( ) 0 0 0 , M ( ) 1 0 1 .
1 0 0
1 1 0

15.

A, B, C, D
2.
Пусть
четыре
города
обслуживаются двумя авиакомпаниями «Ро» и
«Сигма». При этом авиакомпания «Ро» выполняет
прямые рейсы: из A в B, из B в C и D, из C в B, и
авиакомпания «Сигма» выполняет прямые рейсы:
из A в B, из B в C, из D в C. Тогда отношения и
связи городов из множества X { A, B, C, D}
прямыми рейсами соответственно авиакомпаний
«Ро» и «Сигма» имеют вид:
{( A, B), ( B, C ), ( B, D), (C, B)} и {( A, B), ( B, C ), ( D, C )}.

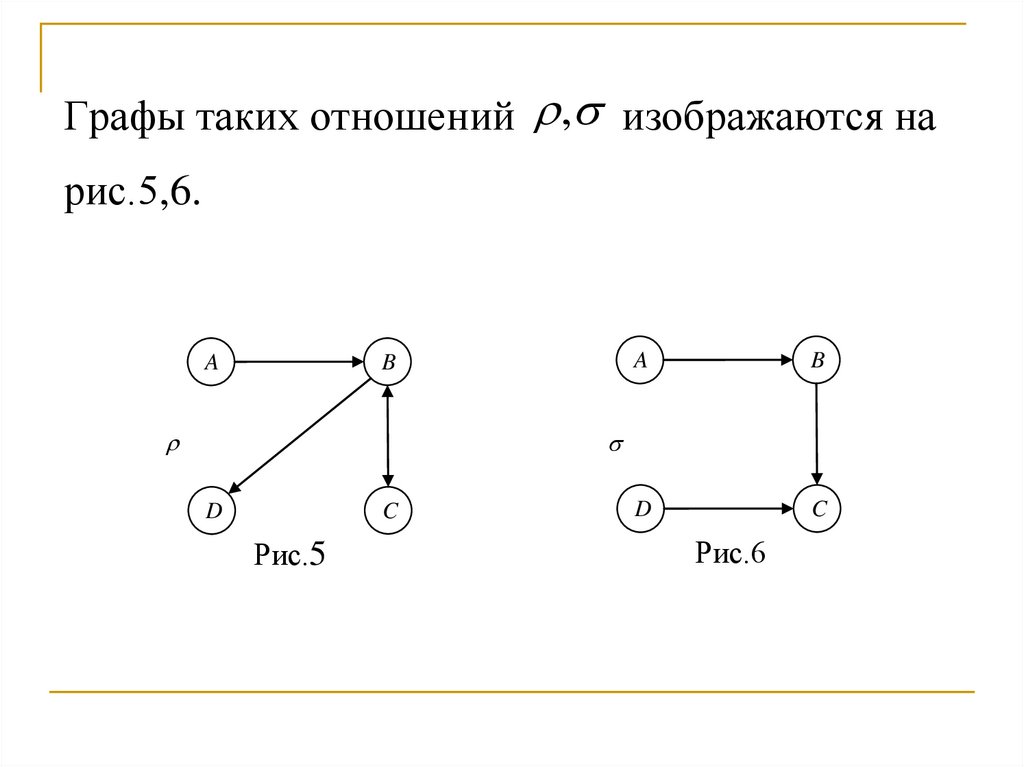
16.

Графы таких отношений , изображаются на
рис.5,6.
A
B
A
B
D
C
D
C
Рис.5
5
Рис.6

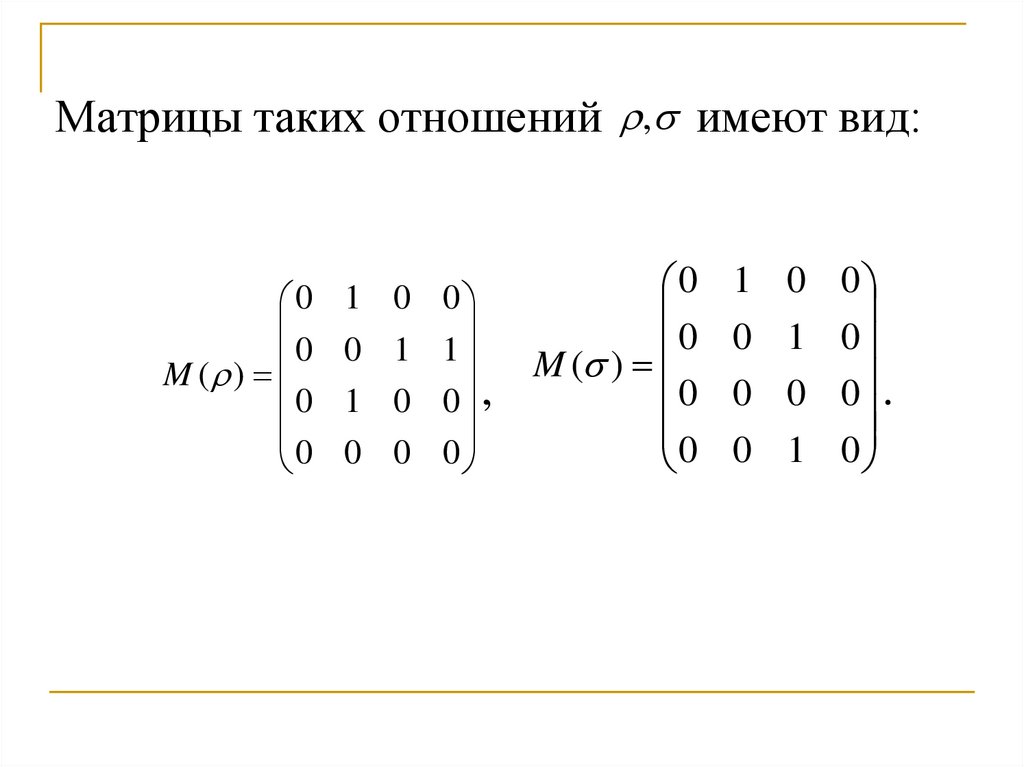
17.

Матрицы таких отношений , имеют вид:
0
0
M ( )
0
0
1
0
1
0
0
1
0
0
0
1
0 ,
0
0
0
M ( )
0
0
1
0
0
0
0
1
0
1
0
0
0 .
0

18.

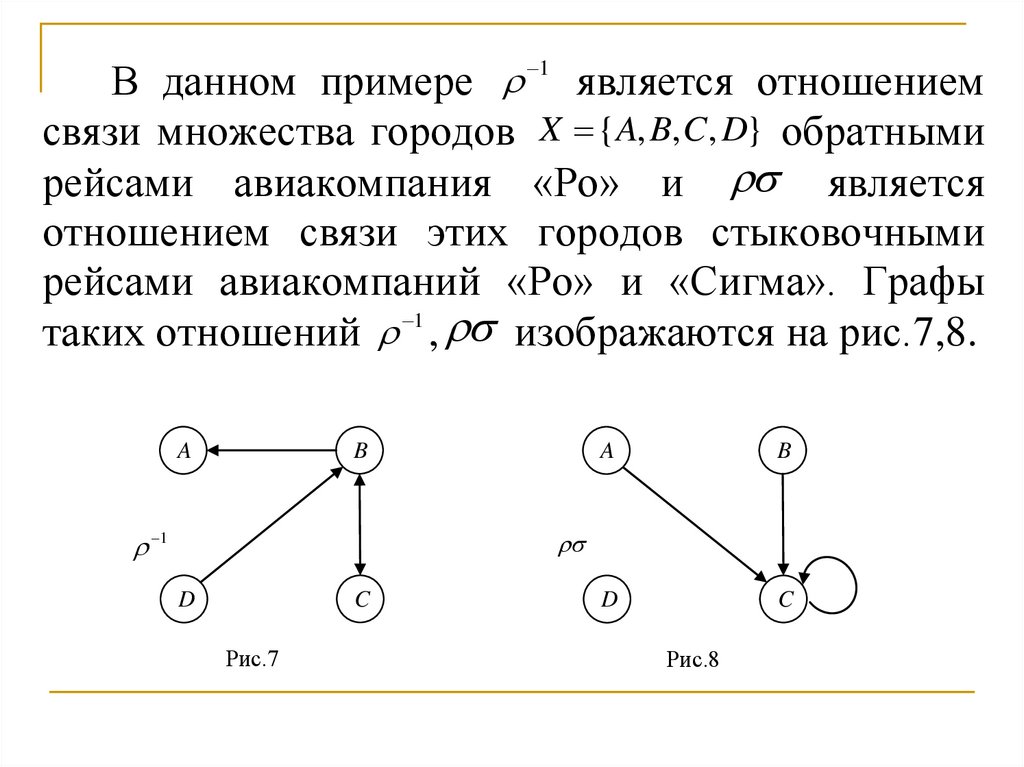
В данном примере 1 является отношением
связи множества городов X {A, B, C, D} обратными
рейсами авиакомпания «Ро» и является
отношением связи этих городов стыковочными
рейсами авиакомпаний «Ро» и «Сигма». Графы
таких отношений 1 , изображаются на рис.7,8.
A
B
A
B
D
C
1
A
B
D
C
D
C
Рис.7
Рис.8

19.

1
Матрицы таких отношений , имеют вид:
0
1
1
M ( )
0
0
0
0
1
1
0
1
0
0
0
0
0 ,
0
0
0
M ( )
0
0
0
0
0
0
1
1
1
0
0
0
0 .
0

20.

Отношение эквивалентности
и фактор-множество

21.

Определение.
Бинарное отношение на множестве A
называется отношением эквивалентности (или
просто
эквивалентностью),
если
оно
рефлексивно, симметрично и транзитивно.
Для
обозначения
эквивалентности
используется инфиксная запись с помощью
символа :
вместо (a, b) пишут a b( ) или просто a b читается «a эквивалентно b относительно
эквивалентности » или просто «a эквивалентно
b».

22.

(a)
Cрезы
называются
классами
эквивалентности по отношению и сокращенно
обозначаются символом [a] .
Множество всех таких классов эквивалентности
{[a] : a A}
называется
фактор-множеством
множества A по эквивалентности
и
обозначается символом A/ .
Характерное свойство: для любых элементов
a,b A условие [a] [b] влечет [a] [b] .

23.

Множество A/ ={[a] : a A} образует семейство
непересекающихся подмножеств множества A,
объединение которого дает все множество A и
которое называется разбиением множества A .
Теорема. Непустое семейство { Ai : i I } подмножеств
множества A в том и только том случае является
разбиением множества A, если это семейство
является фактор-множеством некоторого отношения
эквивалентности на множестве A.
Доказательство.

24.

Определение. Ядром отображения : A B
называется бинарное отношение ker
на
множестве A, которое определяется по формуле
ker {(a, b) A2 : (a ) (b)}.
Определение. Каноническим отображением
эквивалентности называется отображение nat
множества A на фактор множество A/ , которое
каждому элементу a A ставит в соответствие
содержащий его класс эквивалентности [a] .
Легко видеть, что ker nat = .

25.

Определение. Подмножество T A называется
полной системой представителей классов
эквивалентности на множестве A, если:
1) (T ) A ,
2) из условия t1 t 2 ( ) следует t1 t 2 .
Классы эквивалентности [t ] A / могут быть
отождествлены со своими представителями t и
фактор-множество A/ может быть отождествлено
с множеством T.

26.

Примеры.
1. Пусть A – множество шаров в коробке, состоящее из 7
красных, 5 синих и 8 зеленых шаров. Определим на множестве A
отношение по формуле: для любых шаров a,b A условие a b( )
означает, что шары a,b одного цвета.
Отношение рефлексивно, симметрично и транзитивно, т.е.
является эквивалентностью на множестве A. Любой красный шар
aк A определяет класс эквивалентности [ a к ] , состоящий из 7
красных шаров, любой синий шар aс A определяет класс
эквивалентности [aс ] , состоящий из 5 синих шаров и любой
зеленый шар a з A определяет класс эквивалентности [a з ] ,
состоящий из 8 зеленых шаров. Значит, фактор-множество A/
состоит из трех элементов [aк ] , [aс ] , [a з ] и может быть
отождествлено с полной системой представителей классов
эквивалентности на множестве A, состоящей из трех
разноцветных шаров {aк , aс , a з } , или просто с множеством трех
цветов {красный, синий, зеленый}.

27.

2. Пусть A=Z – множество целых чисел. Определим на
множестве Z отношение по формуле: для любых a,b Z
условие a b( ) означает, что числа a,b имеют одинаковые
остатки при делении на число 3, т.е. разность a b кратна
числу 3.
Отношение рефлексивно, симметрично и транзитивно,
т.е. является эквивалентностью на множестве Z. Ясно, что
число 0 определяет класс эквивалентности [0] {0, 3, 6,...},
число
1
–
класс
эквивалентности
[1] {1,1 3,1 6,...} {..., 5, 2,1,4,7,...} ,
число
2
–
класс
эквивалентности [2] {2,2 3,2 6,...} {..., 4, 1,2,5,8,...}. Так как
этими множествами исчерпываются все классы данной
эквивалентности , то фактор-множество Z/ состоит из трех
элементов [0] , [1] , [2] и может быть отождествлено с полной
системой представителей классов эквивалентности на
множестве Z - трехэлементным множеством {0,1,2} .

28.

Задача
представления данных

29.

Постановка задачи:
Имеется множество объектов A , на котором
задано отношение эквивалентности .
Требуется
найти
полную
систему
представителей классов T A эквивалентности
на множестве A , т.е. в каждом классе
эквивалентных объектов выбрать единственного
представителя этого класса.

30.

Примеры задач представления данных:
1) Представление целых чисел.
2) Представление
многочленов
с
одной
переменной.
3) Представление многочленов с несколькими
переменными.
4) Представление матриц.