Пересечение прямой линии с поверхностью

1.

Начертательная
геометрия

2.

Пересечение прямой
линии с поверхностью

3.

Пересечение прямой
линии с гранной
поверхностью

4.

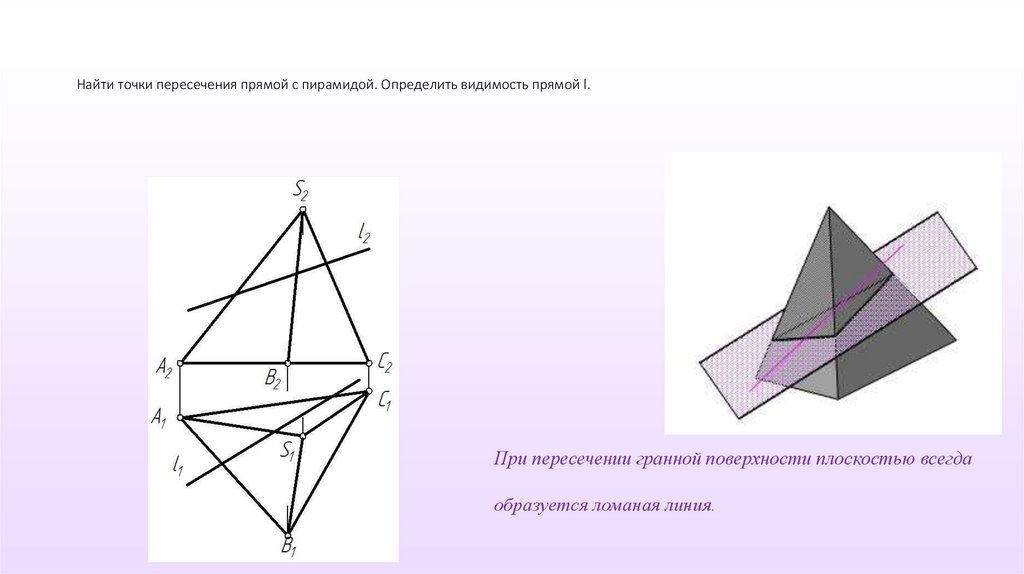
Найти точки пересечения прямой с пирамидой. Определить видимость прямой l.
При пересечении гранной поверхности плоскостью всегда
образуется ломаная линия.

5.

1.
2.
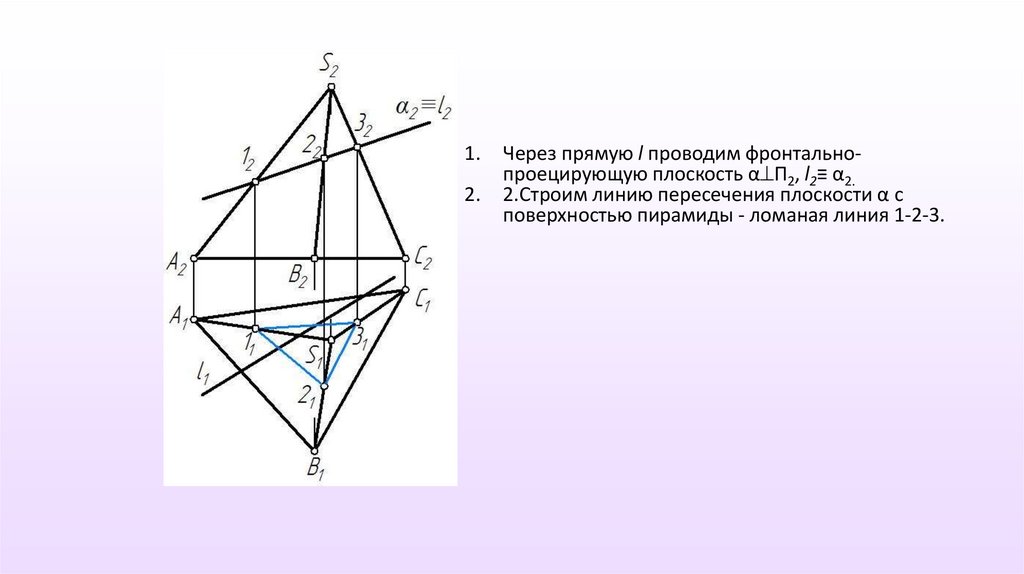
Через прямую l проводим фронтальнопроецирующую плоскость α П2, l2≡ α2.
2.Строим линию пересечения плоскости α с
поверхностью пирамиды - ломаная линия 1-2-3.

6.

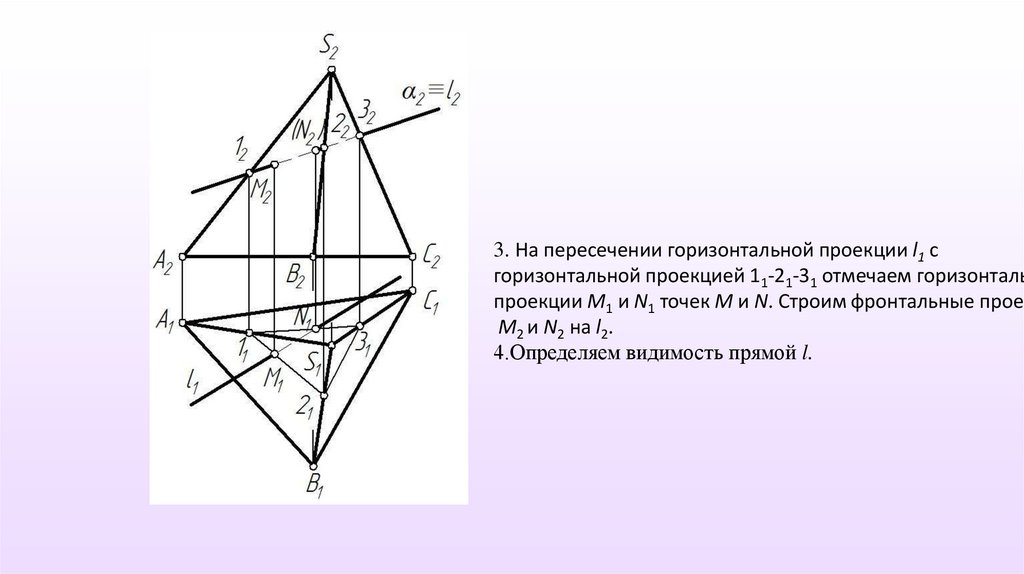
3. На пересечении горизонтальной проекции l1 с
горизонтальной проекцией 11-21-31 отмечаем горизонталь
проекции M1 и N1 точек М и N. Строим фронтальные проек
M2 и N2 на l2.
4.Определяем видимость прямой l.

7.

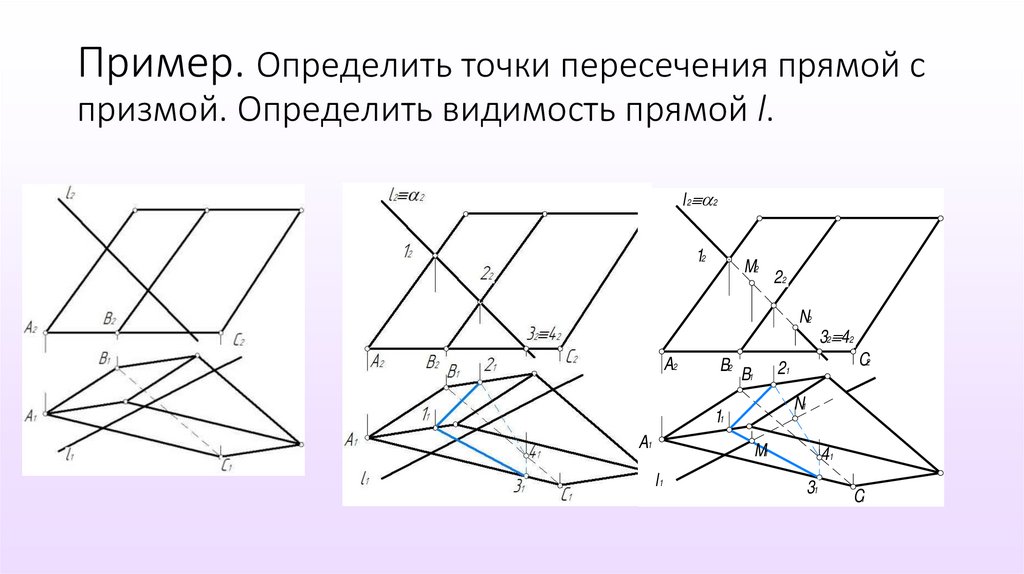
Пример. Определить точки пересечения прямой с
призмой. Определить видимость прямой l.
l 2 2
12
M2
22
N2
A2
B2
C2
21
B1
N1
11
A1
M1
l1
32 42
41
31
C1

8.

Пересечение прямой
линии с конической
поверхностью

9.

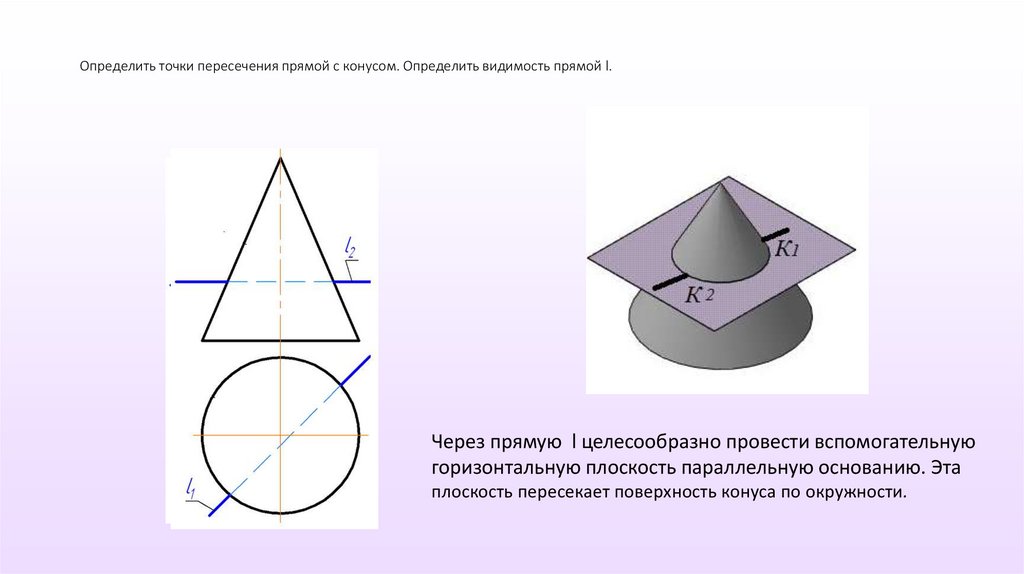
Определить точки пересечения прямой с конусом. Определить видимость прямой l.
Через прямую l целесообразно провести вспомогательную
горизонтальную плоскость параллельную основанию. Эта
плоскость пересекает поверхность конуса по окружности.

10.

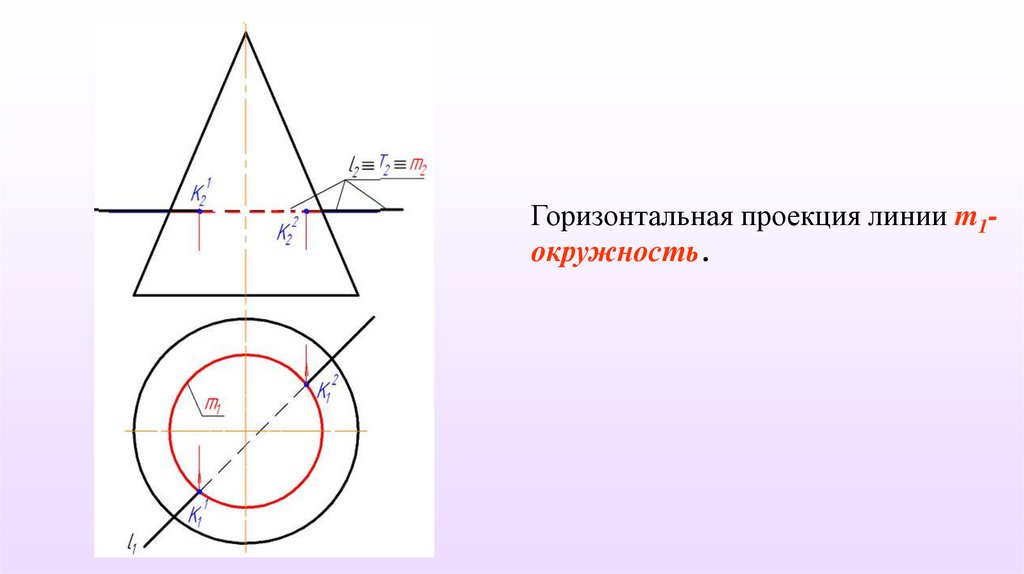
N2
Горизонтальная проекция линии m1окружность .
M2
M1
N1

11.

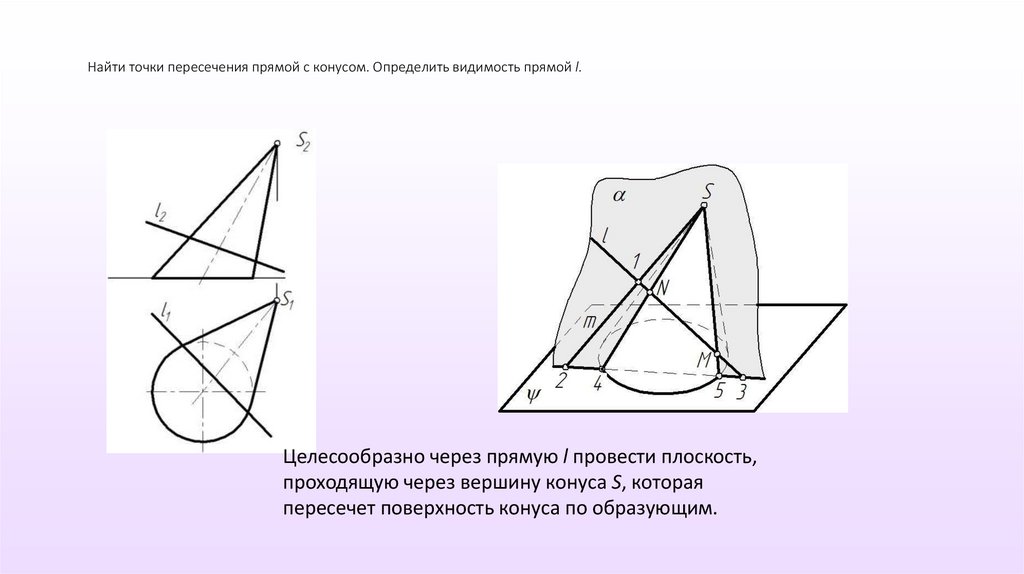
Найти точки пересечения прямой с конусом. Определить видимость прямой l.
Целесообразно через прямую l провести плоскость,
проходящую через вершину конуса S, которая
пересечет поверхность конуса по образующим.

12.

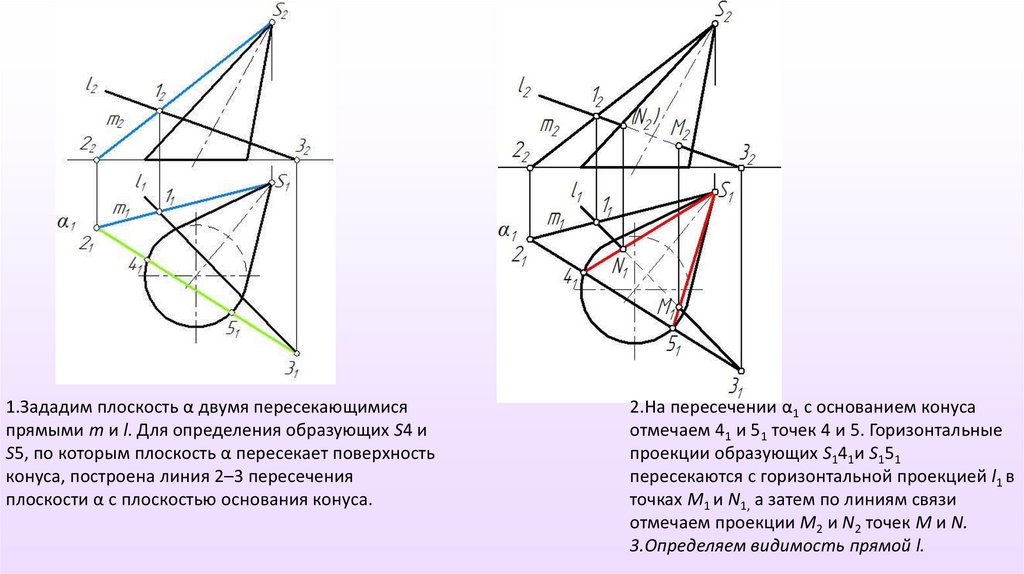
1.Зададим плоскость α двумя пересекающимися
прямыми m и l. Для определения образующих S4 и
S5, по которым плоскость α пересекает поверхность
конуса, построена линия 2–3 пересечения
плоскости α с плоскостью основания конуса.
2.На пересечении α1 с основанием конуса
отмечаем 41 и 51 точек 4 и 5. Горизонтальные
проекции образующих S141и S151
пересекаются с горизонтальной проекцией l1 в
точках М1 и N1, а затем по линиям связи
отмечаем проекции М2 и N2 точек М и N.
3.Определяем видимость прямой l.

13.

Пересечение прямой
линии с
цилиндрической
поверхностью

14.

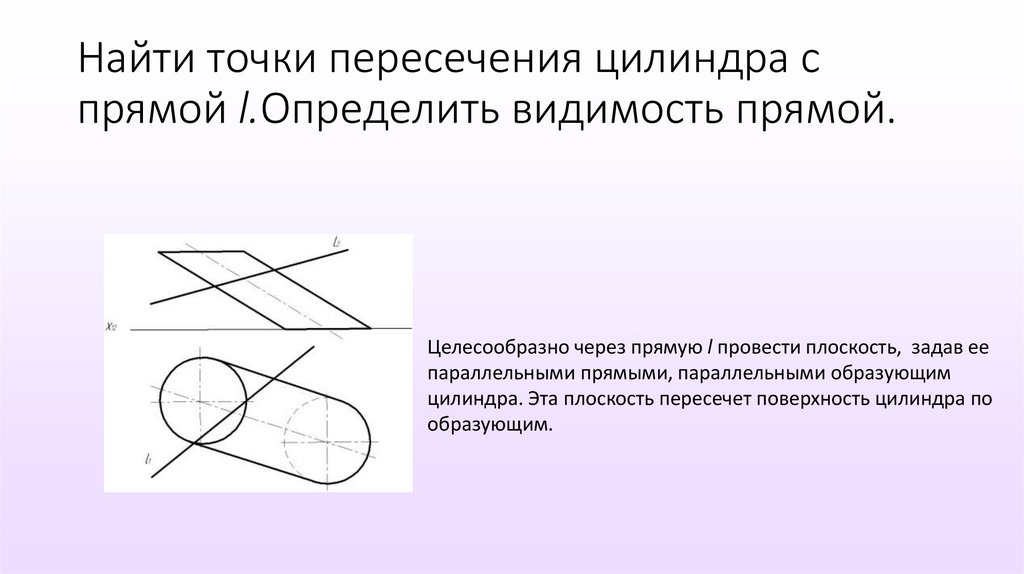
Найти точки пересечения цилиндра с
прямой l.Определить видимость прямой.
Целесообразно через прямую l провести плоскость, задав ее
параллельными прямыми, параллельными образующим
цилиндра. Эта плоскость пересечет поверхность цилиндра по
образующим.

15.

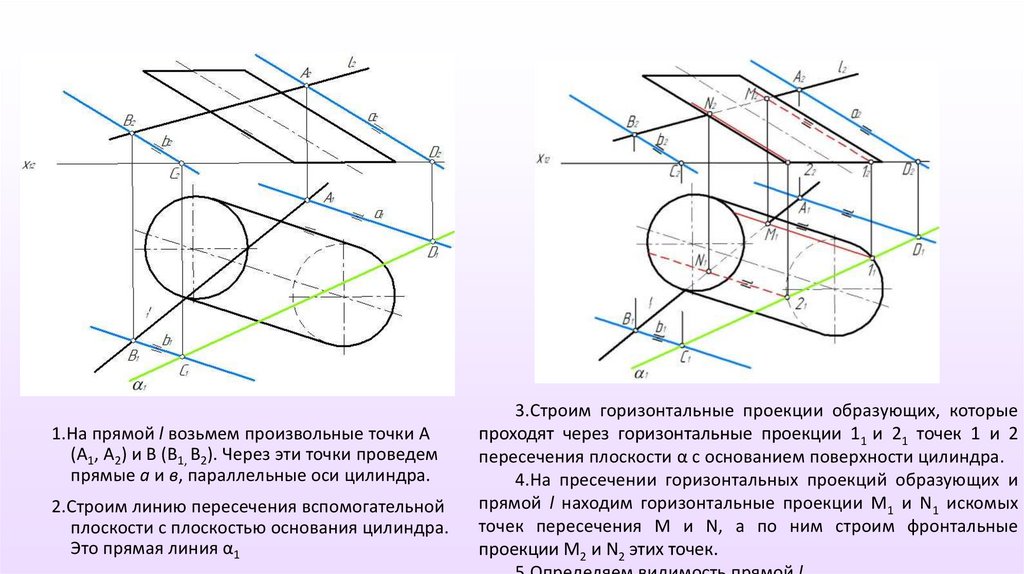
1.На прямой l возьмем произвольные точки А
(А1, А2) и В (В1, В2). Через эти точки проведем
прямые а и в, параллельные оси цилиндра.
2.Строим линию пересечения вспомогательной
плоскости с плоскостью основания цилиндра.
Это прямая линия α1
3.Строим горизонтальные проекции образующих, которые
проходят через горизонтальные проекции 11 и 21 точек 1 и 2
пересечения плоскости α с основанием поверхности цилиндра.
4.На пресечении горизонтальных проекций образующих и
прямой l находим горизонтальные проекции М1 и N1 искомых
точек пересечения М и N, а по ним строим фронтальные
проекции М2 и N2 этих точек.

16.

Пересечение прямой
линии со сферической
поверхностью

17.

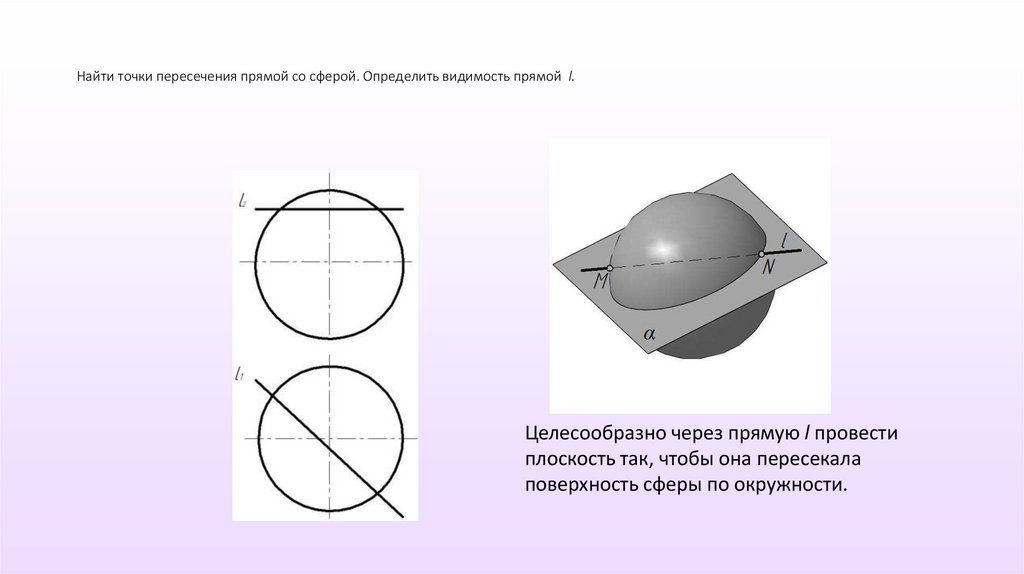
Найти точки пересечения прямой со сферой. Определить видимость прямой l.
Целесообразно через прямую l провести
плоскость так, чтобы она пересекала
поверхность сферы по окружности.

18.

1.
Рационально
провести
горизонтальную плоскость α, l2 ≡ α2
Плоскость α пересекает поверхность
сферы по окружности радиуса R.
2.На пересечении горизонтальной проекции l1
и окружности радиуса R отмечаем искомые
горизонтальные проекции M1 и N1. Фронтальные
проекции M2 и N2 строим на фронтальной проекции
l2 прямой l.
3.Определяем видимость прямой l.

19.

Построить точки пересечения прямой общего положения со сферой. Определить видимость прямой l.

20.

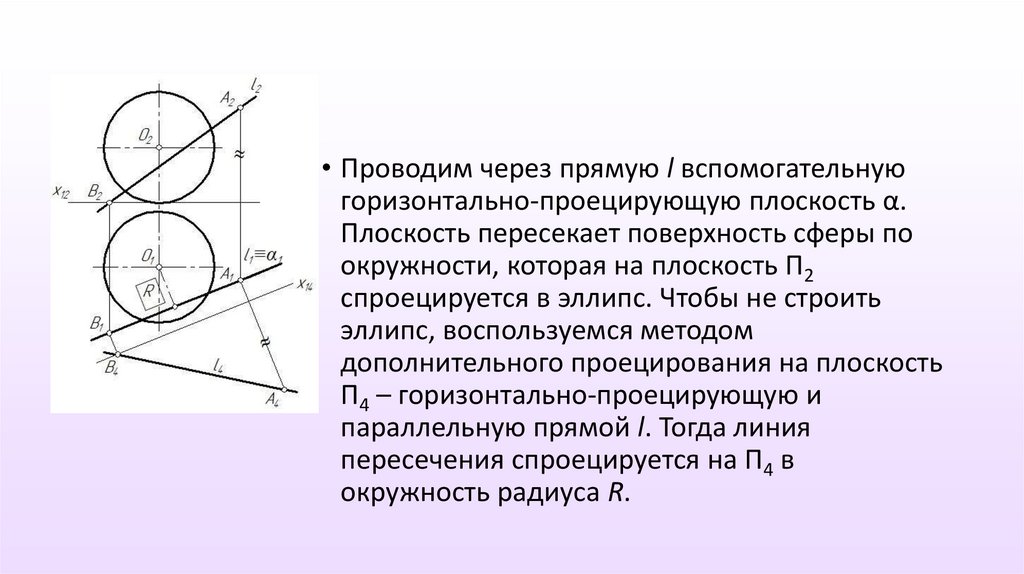
• Проводим через прямую l вспомогательную
горизонтально-проецирующую плоскость α.
Плоскость пересекает поверхность сферы по
окружности, которая на плоскость П2
спроецируется в эллипс. Чтобы не строить
эллипс, воспользуемся методом
дополнительного проецирования на плоскость
П4 – горизонтально-проецирующую и
параллельную прямой l. Тогда линия
пересечения спроецируется на П4 в
окружность радиуса R.

21.

• Строим дополнительную проекцию
прямой АВ на плоскость П4 . На
пересечении отмечаем
дополнительные проекции точек М4
и N4. Затем строим горизонтальную
и фронтальную проекции точек М и
N. Видимость прямой l установлена
по видимости точек М и N.