Множества. Комбинаторика

1.

МНОЖЕСТВА
Комбинаторика

2.

Понятие множества
В 70-х годах XIX века немецкий математик
Георг Кантор(1845-1918) предложил новое
математическое понятие – множество,
т.е.набор,совокупность объектов(или
предметов), объединенных каким-либо
общим признаком.
Например, множество городов России.
Элементом этого множества является
город Курск.

3.

Подмножество
Множество А называют подмножеством
множества В, если каждый элемент
множества А является элементом множества
В. Пустое множество считают подмножеством
любого другого множества.
Например, множество городов Курской
области (Курск, Льгов,
Железногорск,Рыльск…) является
подмножеством множества городов России

4.

5.

6.

Биография Леонарда Эйлера
Леона́рд Э́йлер (15) апреля
1707, Базель, Швейцария
— 7 (18) сентября
1783, Санкт-Петербург,
Российская империя) —
российский и
швейцарский математик,
внёсший значительный
вклад в развитие
математики, а также
механики, физики,
астрономии и ряда
прикладных наук.

7.

Почти полжизни провёл в
России, где внёс
существенный вклад в
становление российской
науки. В 1726 году он был
приглашён работать в
Санкт-Петербург. В 1731—
1741 и, начиная с 1766 года,
был академиком
Петербургской Академии
Наук (в 1741—1766 годах
работал в Берлине,
оставаясь почётным членом
Петербургской Академии).
Хорошо знал русский язык и
часть своих сочинений
(особенно учебники)
публиковал на русском.

8.

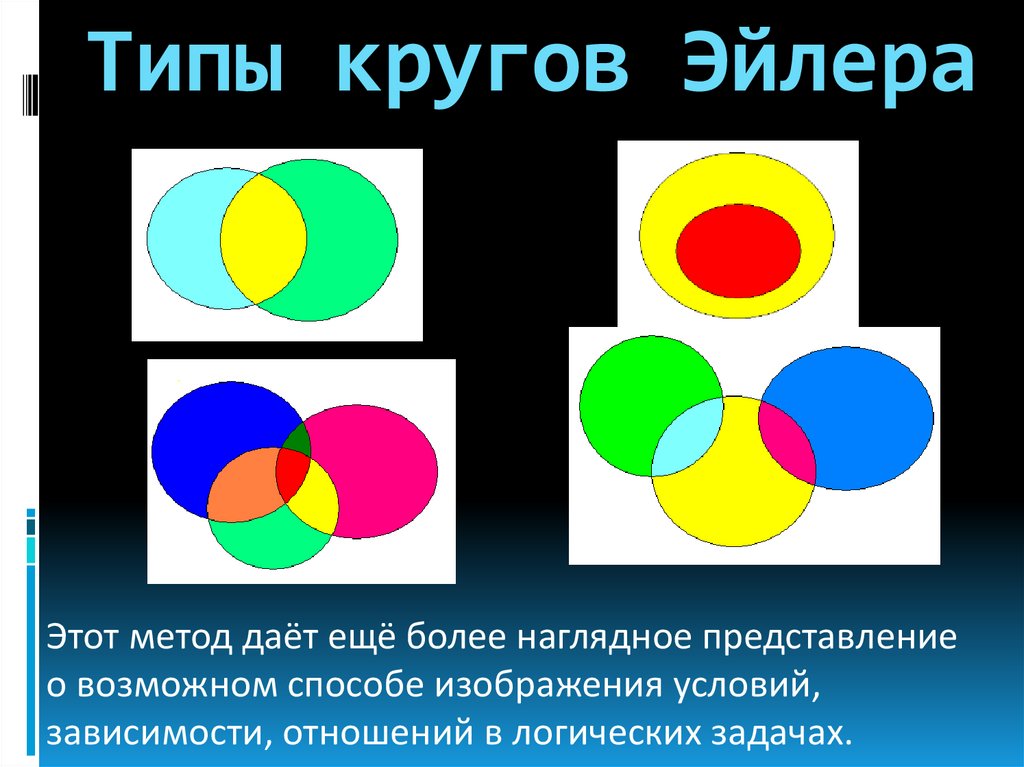
Типы кругов Эйлера
Этот метод даёт ещё более наглядное представление
о возможном способе изображения условий,
зависимости, отношений в логических задачах.

9.

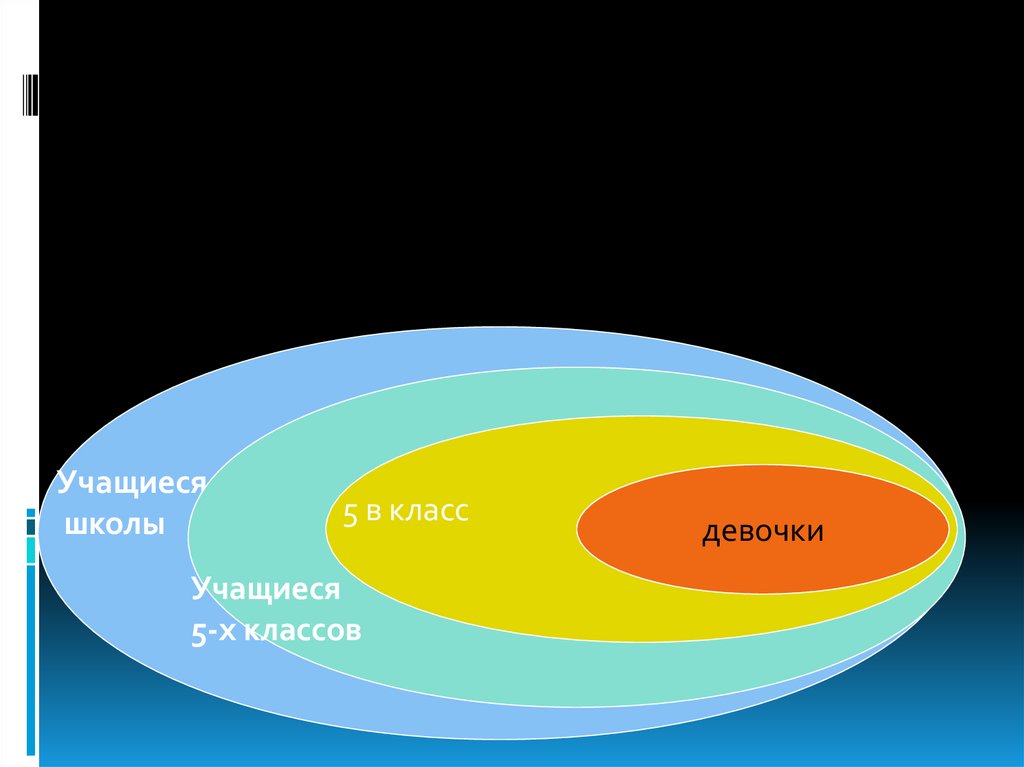
Учащиеся
школы
5 в класс
Учащиеся
5-х классов
девочки

10.

Все мои подруги выращивают в своих квартирах
какие-нибудь растения. Шестеро из них
разводят кактусы, а пятеро — фиалки. И только у
двоих есть и кактусы и фиалки. Угадайте,
сколько у меня подруг?
фиалки
Кактусы
4
2
кф
3
ОТВЕТ : 9 ПОДРУГ

11.

В классе 35 учеников. В математическом
кружке из них 12 занимаются, в
биологическом - 9, а 16 ребят не посещают
эти кружки. Сколько биологов увлекаются
математикой?

12.

Решение. Выполняем рисунок Количество учеников
изобразим с помощью большого круга, а внутри
поместим круги поменьше.
Б-9
М - 12
16
35
16===2719человек
- занимающихся
в каком
9
- биологи
19 -- 712
- ребят
биологи,
не посещающие
мат.
либо
кружке
кружок
увлекавшиеся
математикой

13.

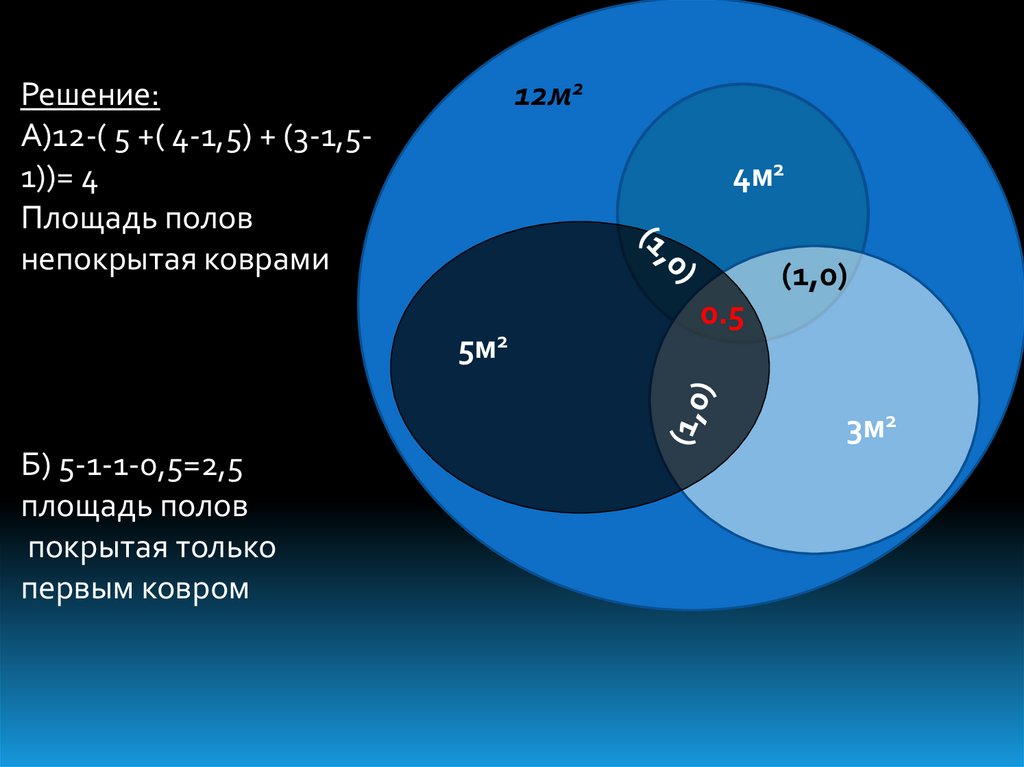
На полу площадью 12м2 лежат три ковра:
площадь одного 5м2, другого - 4м2 и
третьего - 3м2. Каждые два ковра
перекрываются на площади 1,5м2, причем
0,5м2 из этих полутора квадратных метров
приходится на участок пола, где
перекрываются все три ковра. а) Какова
площадь пола, не покрытая коврами? б)
Какова площадь пола, покрытая одним
только первым ковром?

14.

12м2
Решение:
А)12-( 5 +( 4-1,5) + (3-1,51))= 4
Площадь полов
непокрытая коврами
4м2
(1,0)
5м2
0.5
3м2
Б) 5-1-1-0,5=2,5
площадь полов
покрытая только
первым ковром

15.

Комбинаторика
раздел математики, в котором изучаются
вопросы о том, сколько различных
комбинаций, подчинённых тем или иным
условиям, можно составить из заданных
объектов

16.

Решить
комбинаторную задачу - это
значит выписать все возможные
комбинации, составленные из
чисел, слов, предметов и др.,
отвечающих условию задачи.

17.

Решение задачи методом полного перебора всех
возможных вариантов
№1
Сколько двузначных чисел можно
составить, используя цифры 1; 4; 7?
Решение: Для того, чтобы не пропустить и не
повторить ни одного из чисел, будем
выписывать их в порядке возрастания:
11;14;17;(начали с 1)
41;44;47;(начали с 4)
71;74;77;(начали с 7)
Таким образом, из трёх данных цифр
можно составить всего 9 различных
двузначных чисел.
Ответ: 9 чисел.

18.

Решение задач с помощью дерева
возможных вариантов
Существует более общий подход к решению
самых разных комбинаторных задач с
помощью составления специальных схем.
Внешне такая схема напоминает дерево,
отсюда название - дерево возможных
вариантов. При правильном построении
дерева ни один из возможных вариантов
решения не будет потерян.

19.

Дерево возможных вариантов
Никита, Борис, Виктор, и Григорий играли в
шахматы. Каждый сыграл по 1 партии.
Сколько сыграно партий?
Решение.
Никита
Борис
Виктор
Виктор
Григорий
Ответ. 6 партий.
Григорий
Григорий

20.

Таблица
Алла, Бэла, Валентина и Галина во время
майского праздника подарили друг другу по
одному цветку. Причём каждая девочка подарила
каждой по одному цветку. Сколько всего цветков
было подарено?
Решение.
Ответ: 12
цветков.
А
Б
В
Г
А
-----
+
+
+
Б
В
Г
+
+
+
___
+
+
+
---+
+
+
----

21.

Правило умножения
В меню в столовой предложены на выбор 3
первых блюда, 5 вторых и 4 третьих блюд.
Сколько различных вариантов обедов,
состоящих из 1 первого, 1 второго и 1 третьего
блюда, можно составить из предложенного
меню?
Решение.
3*5*4=60
Ответ: 60 блюд.

22.

Правило треугольника
• Встретились 5 приятелей и обменялись
рукопожатиями. Сколько всего сделано
рукопожатий?
• Решение.
1 2 3 4 5
1 - + + + +
2 - - + + +
3 - - - + +
4 - - - - +
5 - - - - - Ответ: 10 рукопожатий.

23.

С помощью графов
По окончанию деловой встречи 4
специалиста обменялись визитными
карточками (каждый вручил свою карточку
каждому). Сколько визитных карточек было
роздано?
Решение.
Ответ. 12 визиток
1
4
2
3

24.

Решите задачу несколькими
способами
Андрей, Борис, Виктор и Григорий после
возвращения из спортивного лагеря
подарили друг другу на память свои
фотографии. Причём каждый мальчик
подарил каждому по 1 фотографии.
Сколько всего фотографий было
подарено?