Аксиоматика Д. Гильберта

1.

Федеральное государственное образовательное учреждение высшего образования
Пензенский государственный университет
Педагогический институт им. В.Г. Белинского
Факультет физико-математических и естественных наук
Кафедра «Математическое образование»
Аксиоматика Д.Гильберта
Подготовили студентки группы
16ФПМ1
Анна Новичкова, Мария Жданова,
Ксения Цветкова, Марина Баранова.
Пенза, 2018

2.

Давид Гильберт (нем. David
Hilbert; 23 января 1862 — 14
февраля 1943) — немецкий
математик-универсал, внёс
значительный вклад в развитие
многих областей математики.
Член многих академий наук, в том
числе Берлинской, Гёттингенской,
Лондонского королевского
общества, иностранный почётный
член Академии наук СССР (1934).
В 1910—1920-е годы (после смерти Анри Пуанкаре) был
признанным мировым лидером математиков.

3.

Пробле́мы Ги́льберта — список из 23 кардинальных проблем математики,
представленный Давидом Гильбертом на II Международном конгрессе
математиков в Париже в 1900 году. Тогда эти проблемы (охватывающие
основания математики, алгебру, теорию чисел, геометрию, топологию,
алгебраическую геометрию, группы Ли, вещественный и комплексный анализ,
дифференциальные уравнения, математическую физику и теорию вероятностей, а
также вариационное исчисление) не были решены.
На данный момент решены 16 проблем из 23. Ещё две не являются корректными
математическими проблемами (одна сформулирована слишком расплывчато,
чтобы понять, решена она или нет, другая, далёкая от решения, — физическая, а
не математическая). Из оставшихся пяти проблем две не решены никак, а три
решены только для некоторых случаев.

4.

Гипотеза ГИЛЬБЕРТА
«А может ли быть все-таки плоскость Лобачевского реализована в
евклидовом трехмерном пространстве в виде полной поверхности
постоянной отрицательной кривизны без особенностей?»
Поставленный вопрос известен как проблема Гильберта.
Д. Гильберт сформулировал эту проблему, исследовал ее и показал,
что в евклидовом трехмерном пространстве таких поверхностей не
существует.

5.

Книга «Основания геометрии»
Свой аксиоматический подход
Гильберт изложил в книге
«Основания геометрии»,
которая появились в первом
издании в 1899 году.

6.

Система аксиом Гильберта ∑г определяет
математическую структуру
S ( M , M , M ; p , p , p , p , p ) + ∑г
1 2 3 1 2 3 4 5
- множество точек
- множество прямых
- множество плоскостей

7.

p1 - отношение принадлежности точки прямой
A a, B a
p2 - отношение принадлежности точки плоскости
A , B
p3 - отношение «лежать между» для трех точек
p4 - отношение конгруэнтности (равенства) отрезка отрезку
DE FG
p5 - отношение конгруэнтности (равенства) угла углу

8.

Система аксиом ∑г состоит из 5 групп
I группа (8 аксиом) содержит аксиомы соединения
(принадлежности), т.е описывает свойства отношений p1 и p2 .
II группа (4 аксиомы) содержит аксиомы порядка, т.е. описывает
отношение p3 и содержит аксиому Паша.
III группа (5 аксиом) содержит аксиомы конгруентности
(равенства), т.е. описывает свойства отношений p4, p5 .
IV группа (2 аксиомы) содержит аксиомы непрерывности:
1-ая аксиома – Аксиома Архимеда
2-ая аксиома – Аксиома Кантора
V группа (1 аксиома) содержит аксиому параллельности

9.

ЗАМЕЧАНИЕ
Д. Гильберт Основания геометрии, 1899г.
У Гильберта последняя аксиома находится в IV группе. А V
группа включает в себя 2 аксиомы непрерывности: аксиома
Архимеда и аксиома линейной полноты.
В большинстве книг по основаниям геометрии эти две
группы меняют местами, а аксиома линейной полноты
заменяется более естественной аксиомой Кантора.

10.

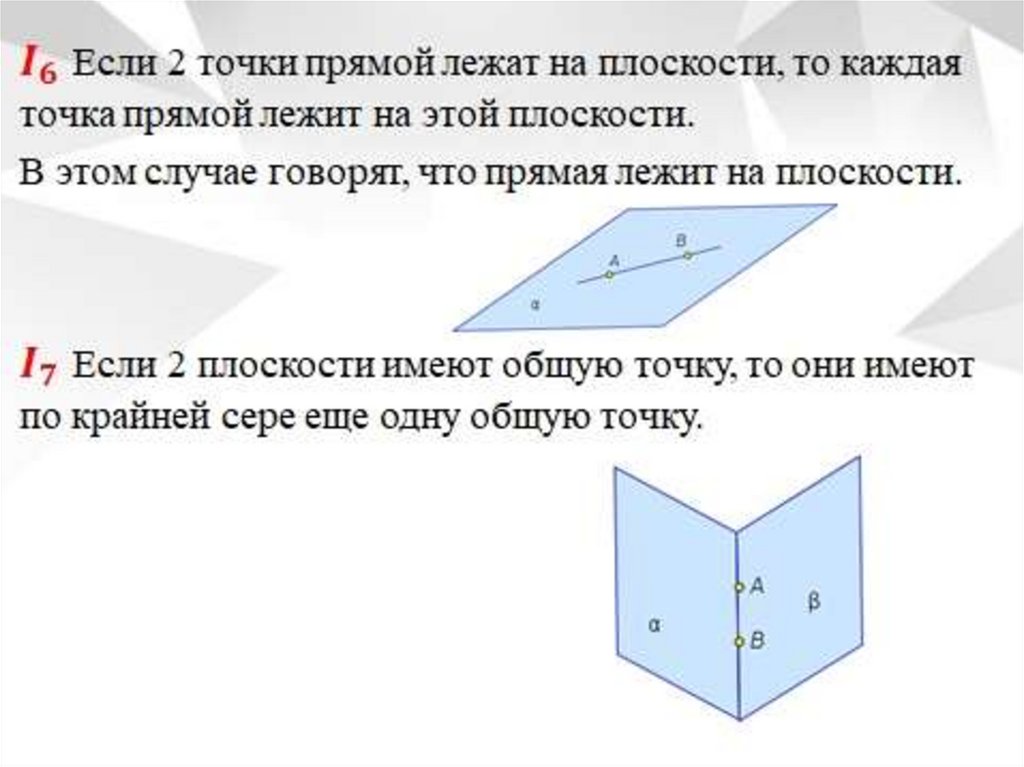
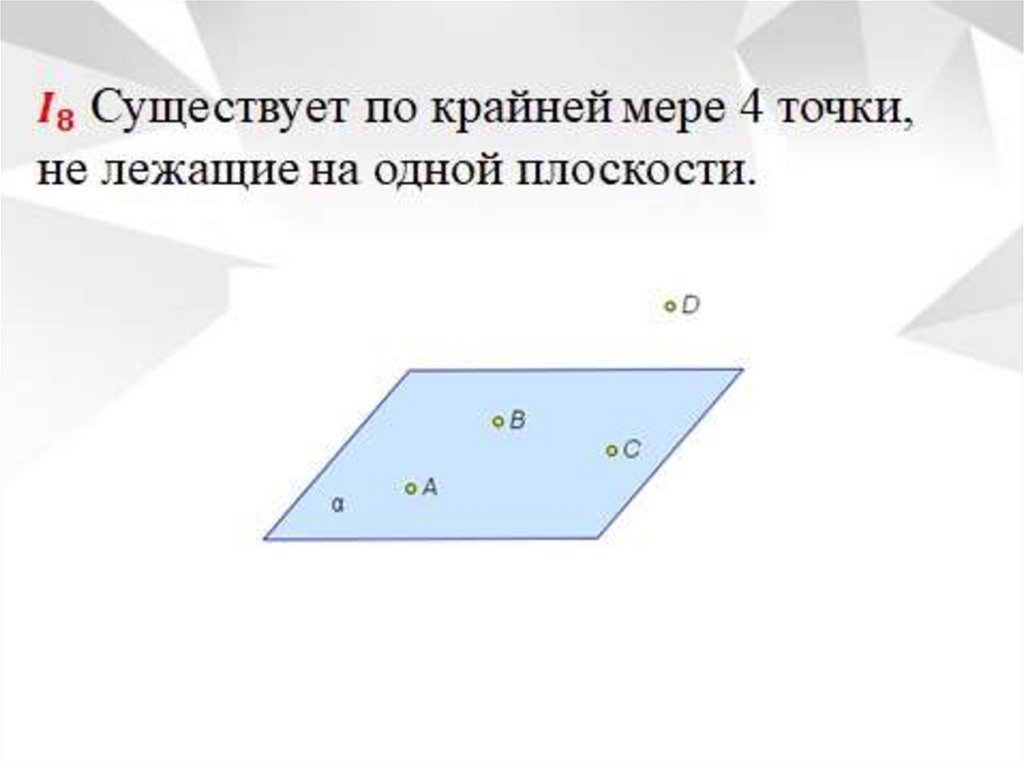
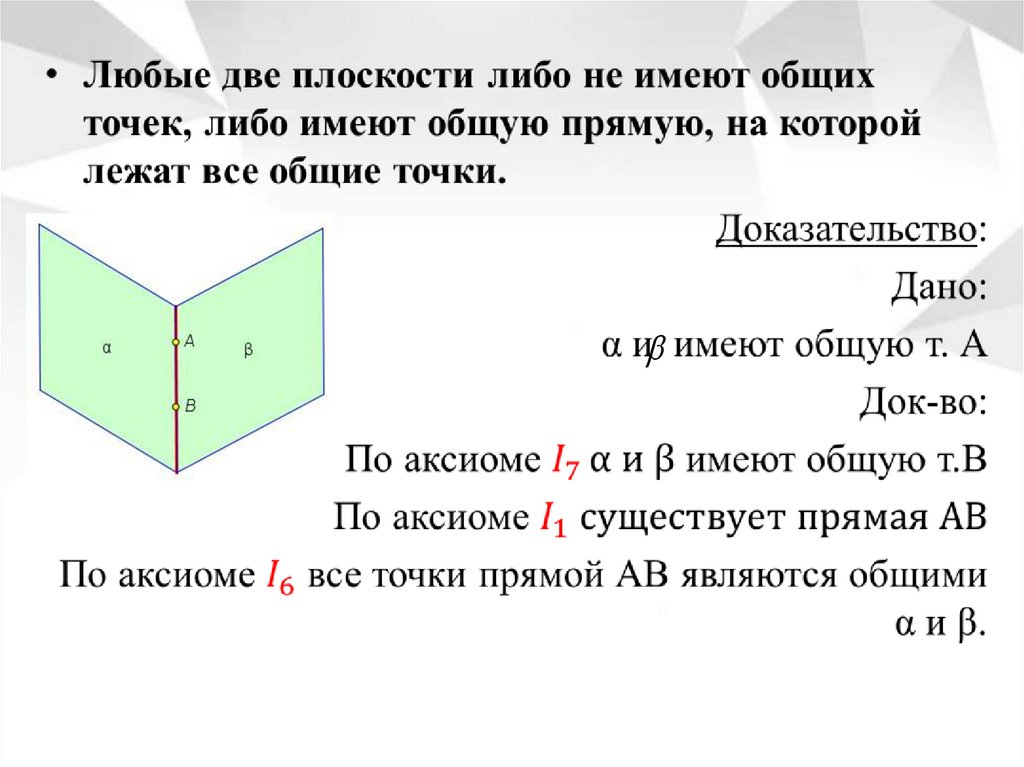
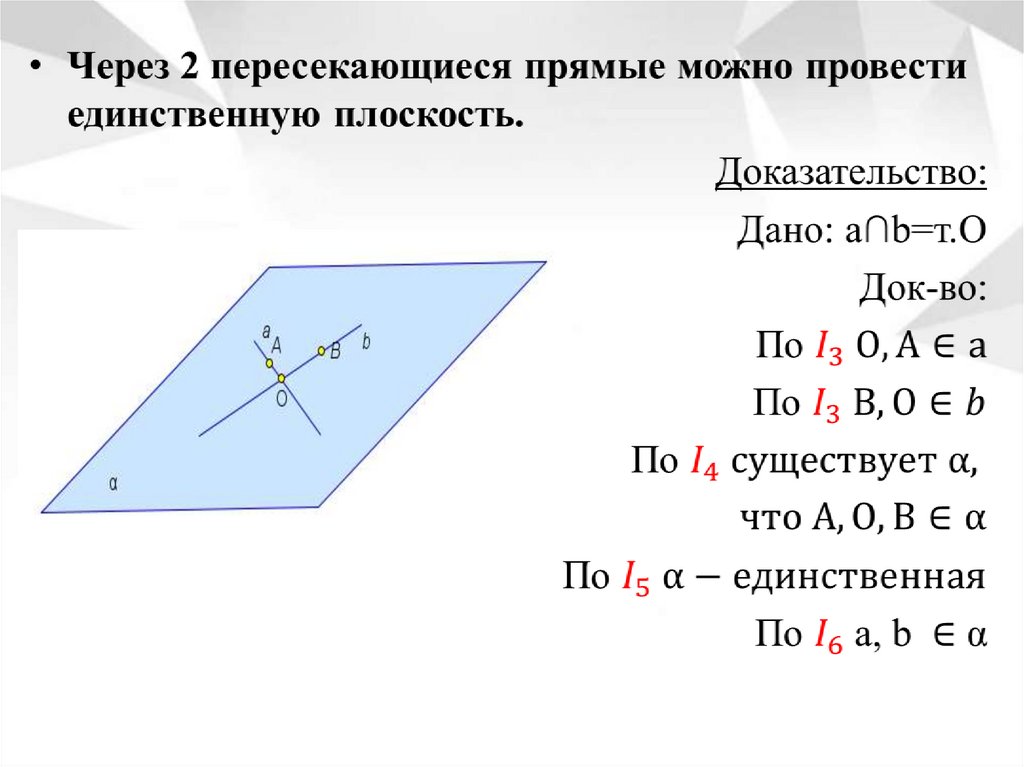
Аксиомы соединения

11.

12.

13.

14.

15.

16.

17.

18.

19.

20.

21.

II группа
Аксиомы порядка
Аксиомы этой группы определяют понятие
«между» трёх точек, что позволяет установить
порядок точек на прямой.

22.

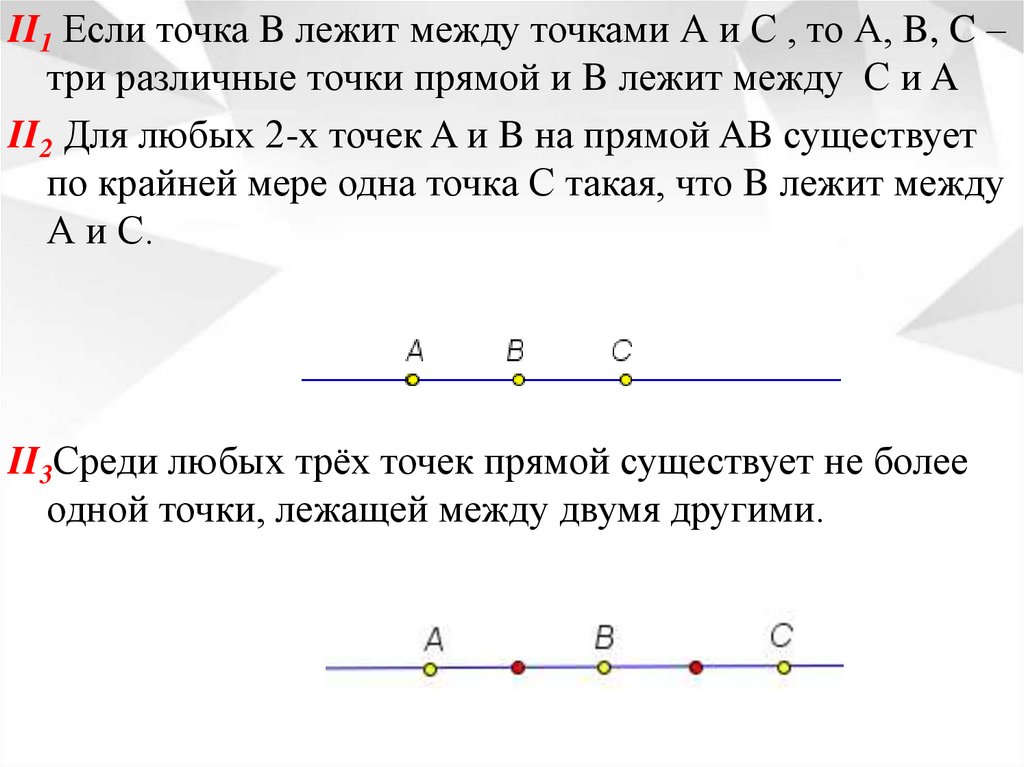
II1 Если точка B лежит между точками А и С , то А, B, C –
три различные точки прямой и B лежит между С и A
II2 Для любых 2-х точек A и B на прямой AB существует
по крайней мере одна точка С такая, что B лежит между
А и С.
II3Среди любых трёх точек прямой существует не более
одной точки, лежащей между двумя другими.

23.

Кроме этих аксиом порядка точек на прямой необходима
еще одна аксиома, относящаяся к порядку точек на
плоскости.
Предварительно Гильберт даёт следующее определение
отрезка:
Д. Гильберт Основания геометрии, 1899г.

24.

II4. Аксиома Паша
Пусть A, B, C –три точки, не лежащие на одной прямой, и
а –прямая в плоскости ABC, не проходящая ни через одну
из точек A,B,C. Если при этом прямая а проходит через
одну из точек отрезка AB, то она должна пройти через
одну из точек отрезка AC или через одну из точек отрезка
BC.
Следствия из аксиом связи и порядка:
Их аксиом II1-3 не следует, что между точками A и B
существуют другие точки. Однако этот факт можно
доказать , подключая аксиому Паша.

25.

Определение треугольника
Совокупность 3-х точек A, B, C не
лежащих на одной прямой и 3-х отрезков их
соединяющих называется треугольником.
Пусть ABC- треугольник, а- прямая в плоскости
∆ ABC , не проходящая ни через одну из вершин
треугольника, если при этом прямая а пересекает одну из
сторон ∆ ABC , например AB, то она должна пересечь либо
стороны AC, либо сторону BC.

26.

C помощью аксиомы Паша можно
доказать следующую теорему:
Теорема 2: Между любыми двумя
точками существует по крайней мере
одна точка. Иначе говоря, на каждом
отрезке существует хотя бы одна
внутренняя точка.
Пусть имеем отрезок AB. По аксиоме I3 существует С ∉ AB.
По аксиоме II2 существует D, C лежит между A и D.
По аксиоме II2 существует E, B лежит между D и E. По аксиоме I1
соединим CE.
Обозначим CE=a. а проходит через С. а пересекает AD. По II4
а пересекает AB или DB, но а не может пересекать DB, т.к. уже
пересекает в E. a ⋂ AB. F не совпадает ни с А, ни с B и Fвнутренняя точка AB.
лежит между A и B.
Применяя эту конструкцию несколько раз, получим между любыми
двумя точками лежит бесконечное число внутренних точек. Из
аксиомы II2 следует, что внешних точек у отрезка бесконечно
много.

27.

Порядок точек на прямой
Используя понятие «между», можем множество всех точек на
прямой упорядочить и превратить это множество во вполне
упорядоченное множество.
Пусть а- прямая, О- некоторая точка. Возьмём A ∈ а , B ∈ a.
Будем говорить, что точки A и B лежат по одну сторону от О,
если, либо А лежит между О и B , либо B лежит между О и А.
Будем говорить, что A, B лежат по разные стороны от О, если О
лежит между А и B.

28.

Возьмем О ∈ а. А ∈ а. Тогда определим луч [O, A).
О- начало луча.
Луч [O, A) –часть прямой а, которая содержит О и
А и все точки лежащие по одну сторону (вместе с
А) точки О.
Возьмём B такую, что O AB
Рассмотрим часть прямой, которая содержит точки О и B и все
точки лежащие вместе с B по одну сторону от О, то получим луч
[O, B) ( полупрямая). О- общее начало.
Лучи ОА и ОВ называются дополняющими до прямой.

29.

О - любая точка делит все оставшиеся точки прямой на
два класса (непустых) непересекающихся, обладающих
следующими свойствами:
1. Если точки A, B принадлежат одному классу, то эти
точки лежат по одну сторону от О.
2. Если точки A, B принадлежат разным классам, то лежат
по разные стороны от О.

30.

Возьмём О ∈ а, тогда О все оставшиеся точки делит на два класса.
Пусть A,B ∈ I.
Будем говорить, что точка А предшествует B, если B AO
С предшествует D, если С OD
I
II
Все точки I класса предшествуют всем точкам второго класса.
Т.о. ввели понятие предшествовать для любых 2-х точек на прямой,
т.е. установили порядок точек на прямой.
Множество точек на прямой является вполне упорядоченным
множеством.
Любые две точки сравнимы A<B.
Порядок определяет направление. Прямая имеет двустороннее
направление.

31.

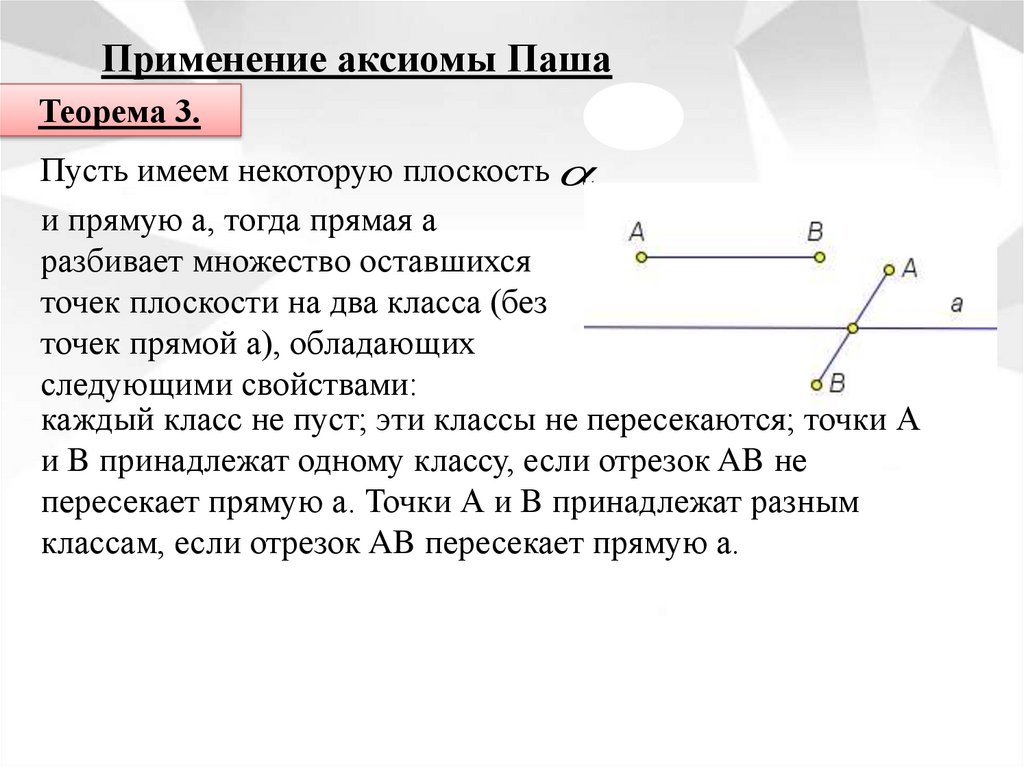
Применение аксиомы Паша
Теорема 3.
Пусть имеем некоторую плоскость
и прямую а, тогда прямая а
разбивает множество оставшихся
точек плоскости на два класса (без
точек прямой а), обладающих
следующими свойствами:
каждый класс не пуст; эти классы не пересекаются; точки А
и B принадлежат одному классу, если отрезок AB не
пересекает прямую а. Точки А и B принадлежат разным
классам, если отрезок AB пересекает прямую а.

32.

Доказательство :
Пусть P не лежит на а, в первый класс собёрем все точки,
такие, что отрезок PA не пересекает прямую а.
Нужно доказать, что если соединить любые две точки I
класса, то отрезок AA не пересекает а.
PA не
пересекает а, PA’ не пересекает а. Следовательно по
аксиоме Паша AA’не пересекает а. Если
предположить, что AA’ пересекает а, то прямая а
должна пересекать либо PA, либо PA’ ( по аксиоме
Паша), но в первый класс мы собрали такие точки A,
что PA не пересекает а и PA’ не пересекает а, поэтому
AA’ не пересекает а.
На прямой а есть хотя бы одна т.О.
На прямой PO есть точка Q такая, что О лежит между P и
Q (По аксиоме II2 ).
Отрезок PQ пересекает а. Точка Q не принадлежит I
классу и не лежит на прямой а, следовательно она
определит II класс.
Действуя аналогично соберем все точки B , B’ такие , что QB, QB’ не пересекают прямую
а. По аксиоме Паша BB’ не пересекает а, нужно доказать, что AB пересекает а.
Рассмотрим ∆QBP прямая а пересекает PQ в т.О, значит прямая а пересекает PB (аксиома
Паша).
Рассмотрим ∆APB а пересекает PB, значит она пересечет AB ( аксиома Паша). A и B в
разных классах.

33.

Полуплоскость α1 - часть плоскости, которая
содержит прямую а (граница) и все точки, лежащие по
одну сторону вместе с первым классом.
Полуплоскость α2 - часть плоскости, которая содержит
все точки, лежащие по другую сторону (II класс) и
общую границу (прямая а)

34.

Эквивалентность теоремы 3 и аксиомы Паша
Используя аксиому Паша мы доказали, что прямая разбивает
плоскость на две полуплоскости. Теорема 3 эквивалентна аксиоме
Паша. Для того, чтобы в этом убедиться, достаточно доказать, что
если принять теорему 3 за аксиому, то утверждение Паша будет
теоремой.
Действительно,
Дано: треугольник ABC.
l ⋂ AB (прямая l проходит через внутреннюю точку отрезка AB).
Доказать: прямая l пересечет BC либо AC.

35.

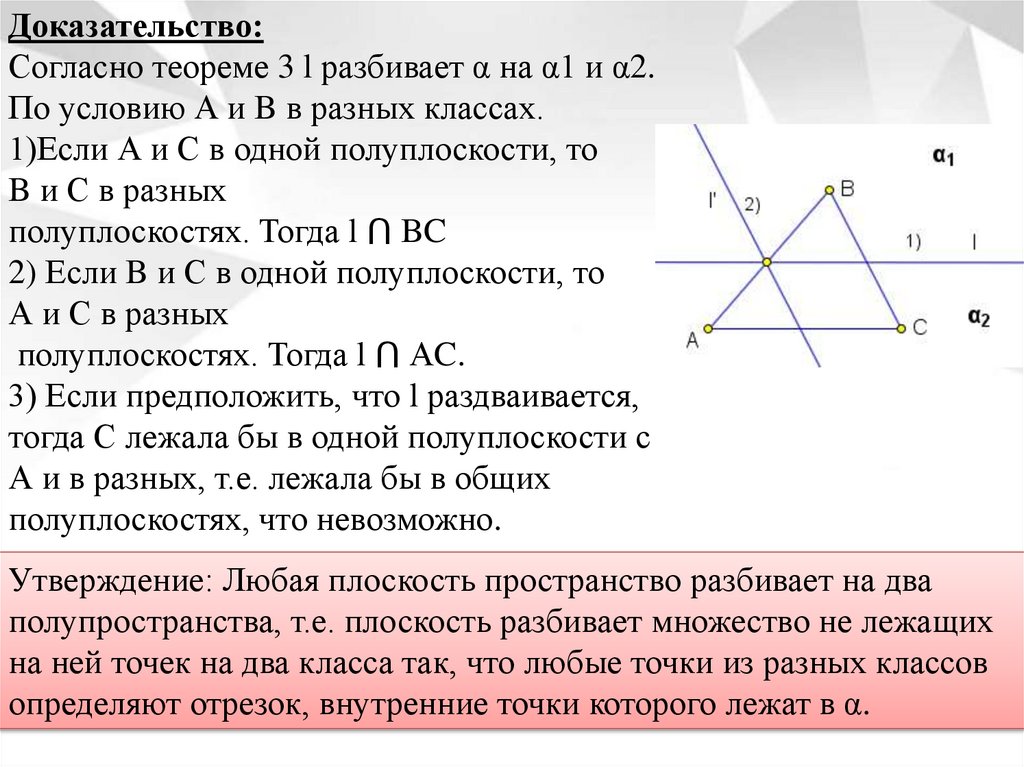
Доказательство:
Согласно теореме 3 l разбивает α на α1 и α2.
По условию А и B в разных классах.
1)Если А и С в одной полуплоскости, то
B и С в разных
полуплоскостях. Тогда l ⋂ BC
2) Если B и С в одной полуплоскости, то
А и С в разных
полуплоскостях. Тогда l ⋂ АC.
3) Если предположить, что l раздваивается,
тогда С лежала бы в одной полуплоскости с
А и в разных, т.е. лежала бы в общих
полуплоскостях, что невозможно.
Утверждение: Любая плоскость пространство разбивает на два
полупространства, т.е. плоскость разбивает множество не лежащих
на ней точек на два класса так, что любые точки из разных классов
определяют отрезок, внутренние точки которого лежат в α.

36.

III группа аксиом
Аксиомы конгруэнтности
(равенства)
В данной группе аксиом перечисляются простейшие
свойства основных отношений: отношения
равенства (конгруэнтности) отрезков и отношения
равенства (конгруэнтности) углов.

37.

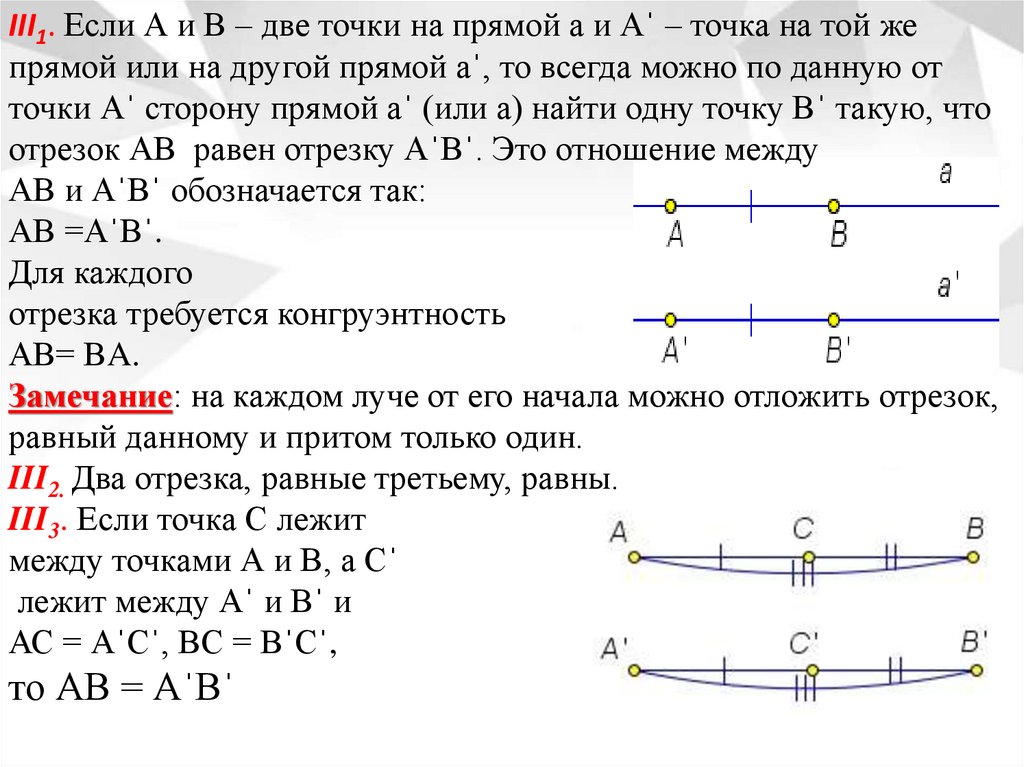
III1. Если А и В – две точки на прямой а и Аˈ – точка на той же
прямой или на другой прямой аˈ, то всегда можно по данную от
точки Аˈ сторону прямой аˈ (или а) найти одну точку Вˈ такую, что
отрезок АВ равен отрезку АˈВˈ. Это отношение между
АВ и АˈВˈ обозначается так:
АВ =АˈВˈ.
Для каждого
отрезка требуется конгруэнтность
АВ= ВA.
Замечание: на каждом луче от его начала можно отложить отрезок,
равный данному и притом только один.
III2. Два отрезка, равные третьему, равны.
III3. Если точка С лежит
между точками А и В, а Сˈ
лежит между Аˈ и Вˈ и
АС = АˈСˈ, ВС = ВˈСˈ,
то АВ = АˈВˈ

38.

Угол – совокупность двух лучей с общим началом,
лежащих на двух разных прямых.
Вершина угла – общее начало угла, а лучи – стороны угла.
НЕ УГОЛ
A
K
Угол, определяемый вершиной О и сторонами h и k,
обозначается так: ∠hOk или ∠АОК
Говорят, что угол отложен от данного луча в заданную от него
в полуплоскость, если второй его луч имеет то же начало и
лежит в заданной полуплоскости.

39.

Пусть hˈ – полупрямая,
дополняющая h до прямой а, а kˈ –
дополняющая k до прямой b.
Плоскость, содержащая прямые а и b,
разбивается прямой a на две
полуплоскости α₁ и α₂.
Прямая b ту же плоскость разбивает так же на две полуплоскости β₁
и β₂. Пусть α₁ - та полуплоскость, которая содержит сторону k ∠hOk,
а β₁ - полуплоскость, содержащая сторону h. Пересечение этих
полуплоскостей называют также углом (плоским углом).
При таком определении угол является «частью плоскости». Точки
плоского угла, не принадлежащие сторонам угла, определяют
внутреннюю область угла. Все остальные точки, не принадлежащие
углу, определяют внешность области угла.

40.

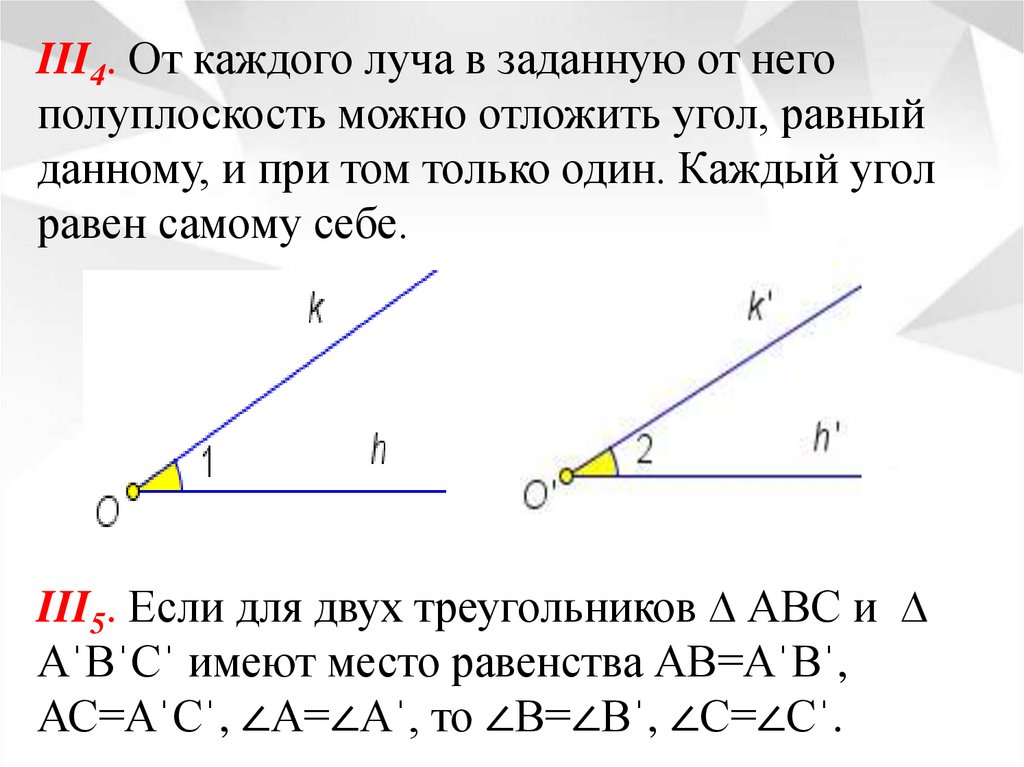
III4. От каждого луча в заданную от него
полуплоскость можно отложить угол, равный
данному, и при том только один. Каждый угол
равен самому себе.
III5. Если для двух треугольников ∆ АВС и ∆
АˈВˈСˈ имеют место равенства АВ=АˈВˈ,
АС=АˈСˈ, ∠А=∠Аˈ, то ∠В=∠Вˈ, ∠С=∠Сˈ.

41.

Равенство треугольников
Два треугольника называются равными, если между
их вершинами можно установить взаимно
однозначное соответствие так, что соответствующие
стороны и соответствующие углы равны.
Запись ∆ АВС = ∆ АˈВˈСˈ означает, что вершины
А и Аˈ, В и Вˈ, С и Сˈ соответствуют друг другу и
справедливы равенства АВ=АˈВˈ, ВС=ВˈСˈ,
АС=АˈСˈ, ∠А=∠Аˈ, ∠В=∠Вˈ, ∠С=∠Сˈ.

42.

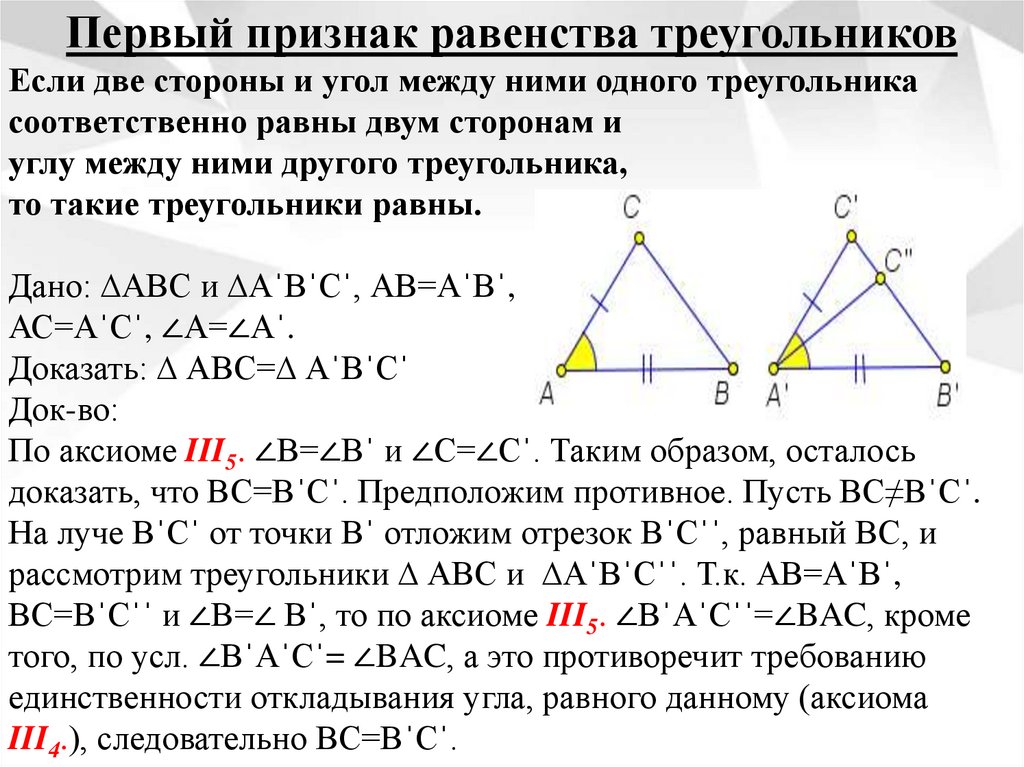
Первый признак равенства треугольников
Если две стороны и угол между ними одного треугольника
соответственно равны двум сторонам и
углу между ними другого треугольника,
то такие треугольники равны.
Дано: ∆АВС и ∆АˈВˈСˈ, АВ=АˈВˈ,
АС=АˈСˈ, ∠А=∠Аˈ.
Доказать: ∆ АВС=∆ АˈВˈСˈ
Док-во:
По аксиоме III5. ∠В=∠Вˈ и ∠С=∠Сˈ. Таким образом, осталось
доказать, что ВС=ВˈСˈ. Предположим противное. Пусть ВС≠ВˈСˈ.
На луче ВˈСˈ от точки Вˈ отложим отрезок ВˈСˈˈ, равный ВС, и
рассмотрим треугольники ∆ АВС и ∆АˈВˈСˈˈ. Т.к. АВ=АˈВˈ,
ВС=ВˈСˈˈ и ∠В=∠ Вˈ, то по аксиоме III5. ∠ВˈАˈСˈˈ=∠BAC, кроме
того, по усл. ∠ВˈАˈСˈ= ∠BAC, а это противоречит требованию
единственности откладывания угла, равного данному (аксиома
III4.), следовательно ВС=ВˈСˈ.

43.

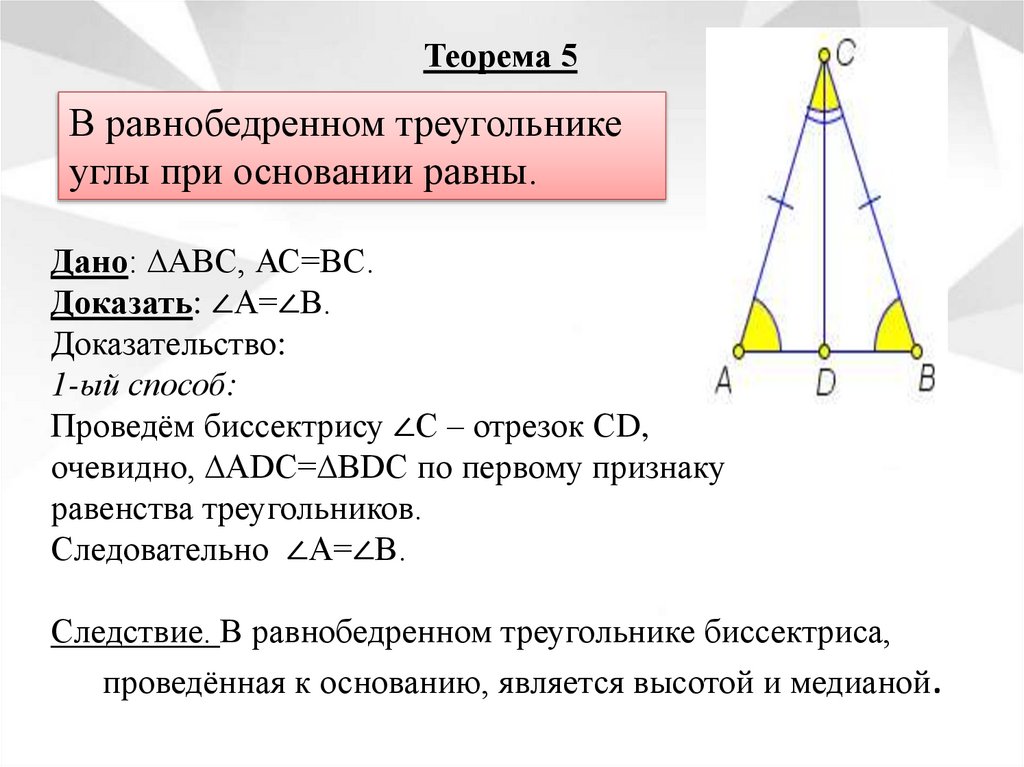
Теорема 5
В равнобедренном треугольнике
углы при основании равны.
Дано: ∆АВС, АС=ВС.
Доказать: ∠А=∠В.
Доказательство:
1-ый способ:
Проведём биссектрису ∠С – отрезок СD,
очевидно, ∆АDC=∆BDC по первому признаку
равенства треугольников.
Следовательно ∠А=∠В.
Следствие. В равнобедренном треугольнике биссектриса,
проведённая к основанию, является высотой и медианой.

44.

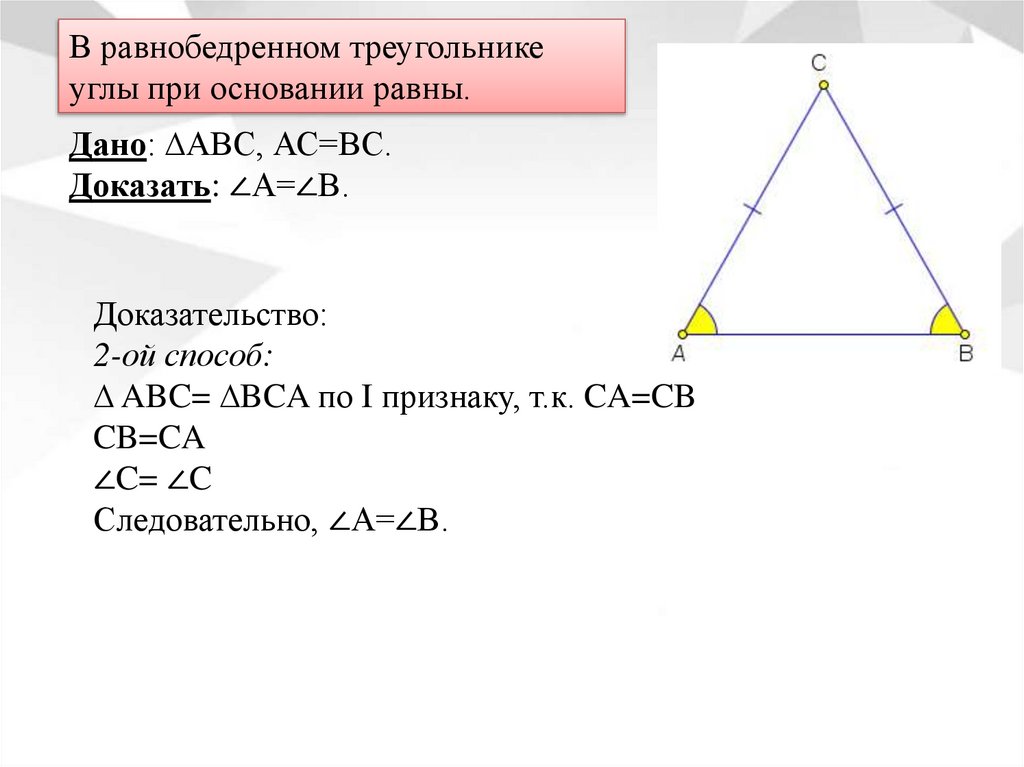
В равнобедренном треугольнике
углы при основании равны.
Дано: ∆АВС, АС=ВС.
Доказать: ∠А=∠В.
Доказательство:
2-ой способ:
∆ ABC= ∆BCA по I признаку, т.к. CA=CB
CB=CA
∠C= ∠C
Следовательно, ∠А=∠В.

45.

46.

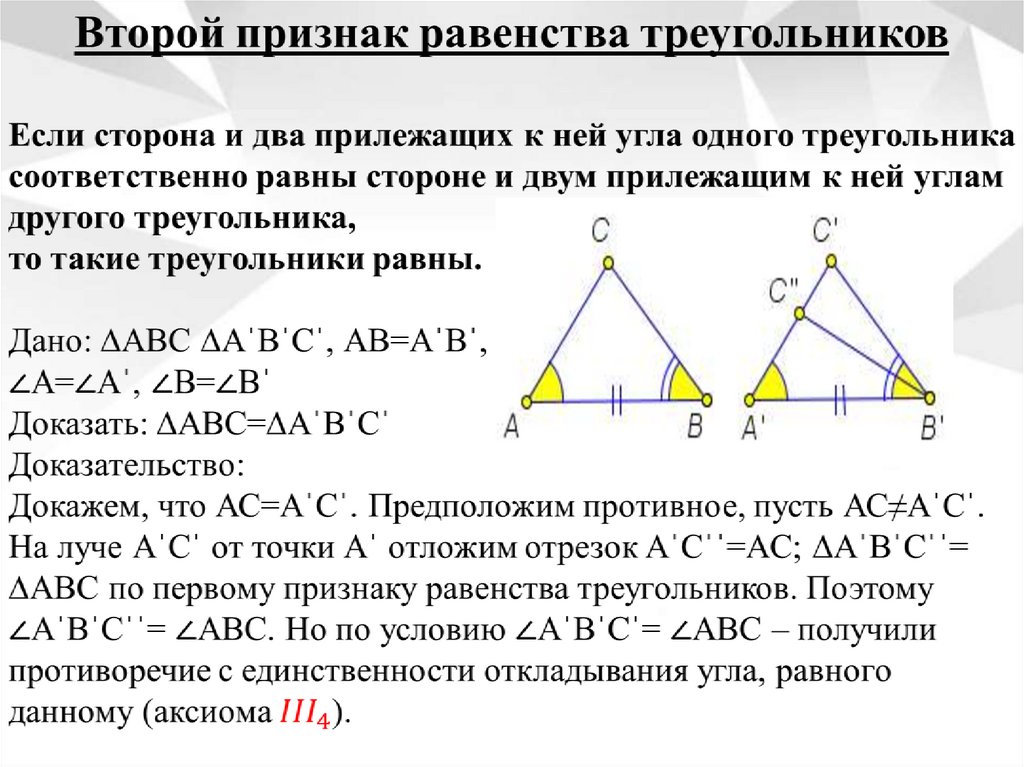
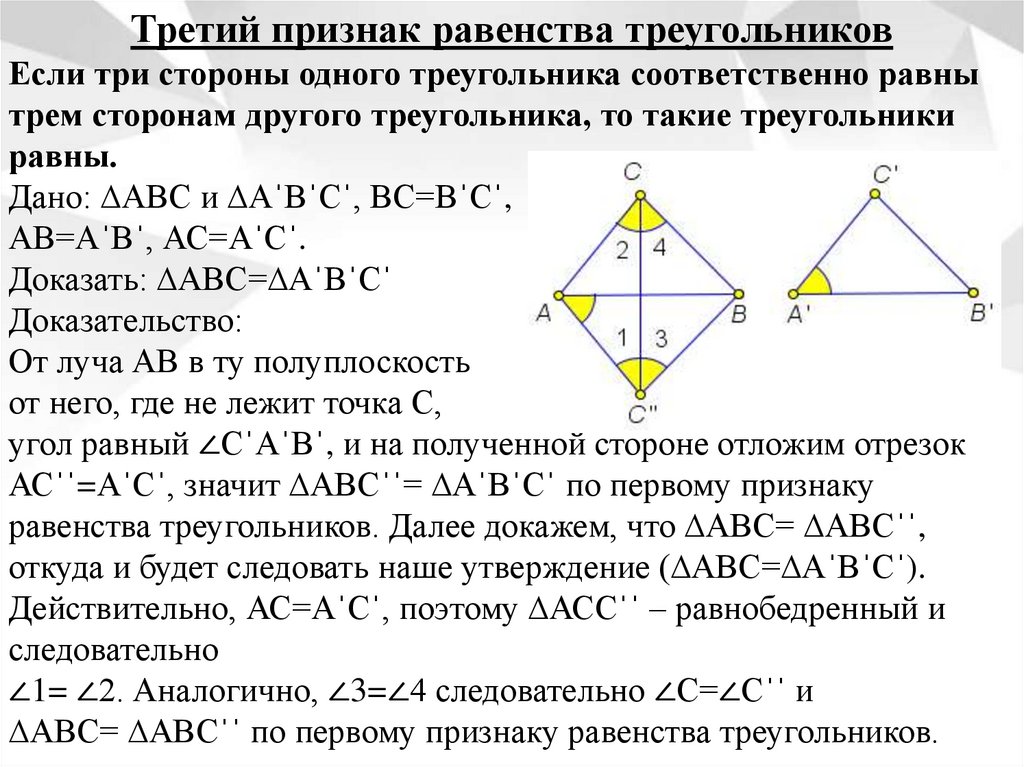
Третий признак равенства треугольников
Если три стороны одного треугольника соответственно равны
трем сторонам другого треугольника, то такие треугольники
равны.
Дано: ∆АВС и ∆АˈВˈСˈ, ВС=ВˈСˈ,
АВ=АˈВˈ, АС=АˈCˈ.
Доказать: ∆АВС=∆АˈВˈСˈ
Доказательство:
От луча АВ в ту полуплоскость
от него, где не лежит точка С,
угол равный ∠СˈАˈВˈ, и на полученной стороне отложим отрезок
АСˈˈ=AˈCˈ, значит ∆АВСˈˈ= ∆АˈВˈСˈ по первому признаку
равенства треугольников. Далее докажем, что ∆АВС= ∆АВСˈˈ,
откуда и будет следовать наше утверждение (∆АВС=∆АˈВˈСˈ).
Действительно, АС=АˈСˈ, поэтому ∆АССˈˈ – равнобедренный и
следовательно
∠1= ∠2. Аналогично, ∠3=∠4 следовательно ∠С=∠Сˈˈ и
∆АВС= ∆АВСˈˈ по первому признаку равенства треугольников.

47.

48.

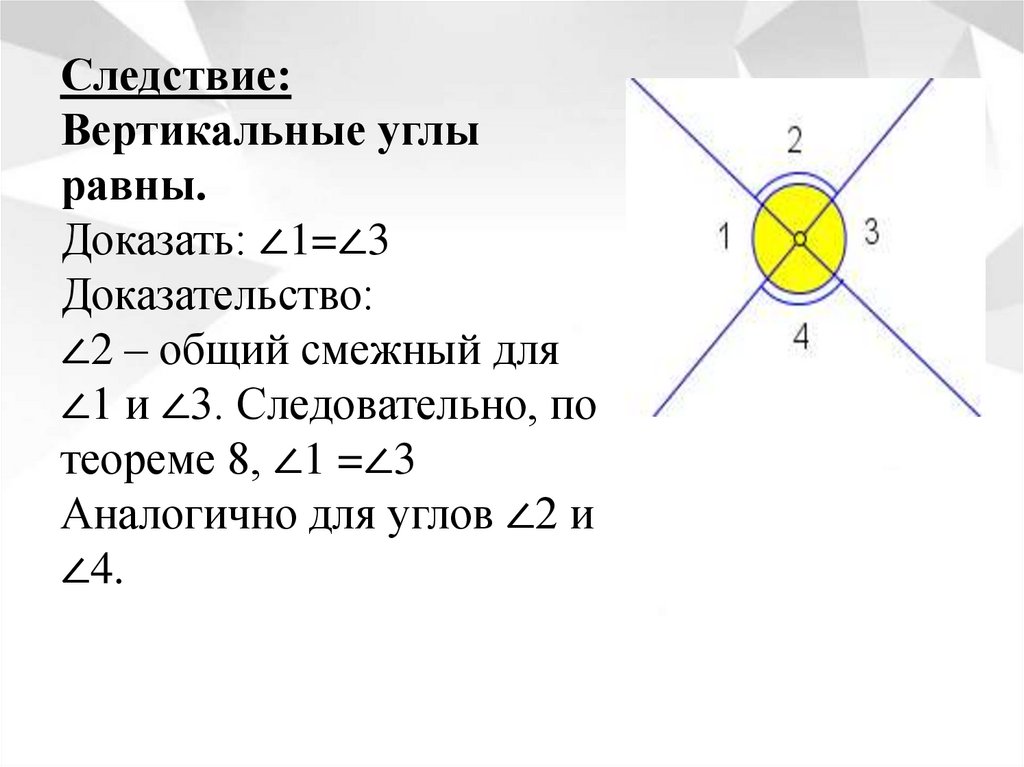
Следствие:
Вертикальные углы
равны.
Доказать: ∠1=∠3
Доказательство:
∠2 – общий смежный для
∠1 и ∠3. Следовательно, по
теореме 8, ∠1 =∠3
Аналогично для углов ∠2 и
∠4.

49.

Теорема 9 (Часть I)
Из любой точки можно опустить на данную прямую один и
только один перпендикуляр.
II. Из каждой точки на прямой можно восстановить
единственный перпендикуляр.
I. Дано: а, А
Док-ть: ∃! АА₀ ⊥а .
Док-во:
1.Существование.
Пусть В∈а, ∠1=∠2, ВС=ВА, ∆АВА₀=∆ВА₀С (по первому признаку)
⇒ ∠АА₀В=∠ВА₀С – смежные ⇒ ∠АА₀В=∠ВА₀С – прямые ⇒ АА₀ ⊥а
2.Единственность.
АА₀ ⊥а и АА₁ ⊥а
∆АА₀А₁=∆СА₀А₁ (по первому признаку) ⇒ ∠АА₁А₀= ∠А₀А₁С
⇒∠А₀А₁С – прямой ⇒∠А₀А₁Р – прямой
∠А₀А₁А =∠А₀А₁С
∠А₀А₁Р =∠А₀А₁С
⇒противоречие с аксиомой III4
I.

50.

Теорема 9 (Часть II)
II. Дано: а, А а
Док-ть: ∃! АА₀ ⊥а .
По доказанному, прямой угол есть, по аксиоме III4
можно отложить только один угол, равный данному.
Следствие: Две прямые перпендикулярные
третьей не пересекаются.
Прямые, которые
лежат в одной плоскости и не
пересекаются, называются параллельными.
Дано: а b, с а
Доказать: b‖c
Доказательство:
Методом от противного. Пусть b и с пересекаются, т.е. b⋂c=P, т.е. из
P мы опустили на прямую а два перпендикуляра, РH₁ a, РН а –
противоречие с Т.9.

51.

Сравнение отрезков
Мы можем ввести понятия: «больше» и «меньше» для сравнения
отрезков.
Возьмём два отрезка AʹBʹ и АВ, по аксиоме III1 на АВ существует
С, такая что АС=АʹВʹ.
Если С лежит между А и В,
то будем говорить, что АВ
больше АʹВʹ (AB˃AʹBʹ)
Если В лежит между А и С,
то будем говорить,
что АВ меньше АʹВʹ (АВ˂АʹВʹ)

52.

Сравнение углов
Мы можем ввести понятия: «больше» и «меньше» для
сравнения углов.
Возьмём два угла:
На луче ОА от точки О
в ту полуплоскость,
где лежит точка В отложим угол ∠АОС=∠АʹОʹВʹ.
Если ОС лежит внутри ∠АОВ, тогда ∠АОВ > ∠AʹOʹBʹ
Если ОС лежит вне ∠АОВ, тогда ∠АОВ < ∠AʹOʹBʹ
• Для любых двух отрезков: либо равны между собой,
либо один больше другого и наоборот.
• Для любых двух углов: либо равны между собой, либо
один больше другого и наоборот.

53.

Теорема 10
Все прямые углы равны между собой.
Дано: ∠kOh – прямой ,
∠kʹOʹhʹ – прямой
Доказать: ∠kOh = ∠kʹOʹhʹ
Доказательство:
Предположим,
что ∠kOh ≠ ∠kʹOʹhʹ
По аксиоме III4. отложим ∠1=∠kOh и ∠2= ∠kOh
∠kOh₁ - смежный для ∠kOh
∠kOh₁=∠3
∠3 – смежный для ∠1
Т.к. ∠kOh - прямой, ∠kOh₁=∠kOh,
∠2=∠3 ∠3 =∠kOh,
противоречие с
∠2= ∠kOh
аксиомой III4.
⇒ ∠kOh = ∠kʹOʹhʹ

54.

IV группа аксиом
Аксиомы непрерывности
IV1 аксиома Архимеда
IV2 аксиома Кантора
В большинстве учебников по основаниям геометрии четвертая и
пятая группы аксиом меняются местами. Такой порядок
перечисления аксиом удобен при изложении проблемы V
постулата Евклида и геометрии Лобачевского.
Геометрия первых четырех групп аксиом называется
абсолютной геометрией. Факты абсолютной геометрии
справедливы как в геометрии Евклида, так и в геометрии
Лобачевского.

55.

IV1
(аксиома Архимеда). Пусть AB и CD –
произвольные отрезки. Тогда на прямой AB
существует конечное число точек A1, A2,… , An ,
расположенных так, что точка A1 лежит между
точками A и A2 , точка A2 лежит между A1 и A3 и т.д.,
причем отрезки AA1, A1A2,… , An-1 An равны отрезку
CD, а точка В лежит между A и An .
n CD AB

56.

IV2 (аксиома Кантора). Пусть на прямой а дана любая
бесконечная последовательность отрезков
A1B1, A2B2 ,…, из которых каждый последующий лежит
внутри предыдущего, и какой бы ни был отрезок,
найдется n, что отрезок AnBn меньше этого отрезка.
Тогда существует точка X, лежащая внутри всех этих
отрезков.
[
A
1
[
[
A
2
X
] ]B ]B
2
1

57.

Докажем, что точка X единственная.
Доказательство проведем методом от противного.
Пусть существует еще одна точка Y, которая принадлежит
всем отрезкам последовательности. Тогда отрезок XY
принадлежит всем отрезкам. Но по условию, какой бы ни
был отрезок, найдется такое n, что AnBn меньше этого
отрезка. В данном случае отрезок AnBn при любом n
больше отрезка XY, что исключается условием теоремы.
[
A
1
[
[
A
2
Y
X
] ]B ]B
2
1
Прямая является непрерывной (связной), т.к. если бы такой
точки X не существовало, то в этом месте был бы «разрыв»
прямой, она не была бы «сплошной».

58.

Длина отрезка
Пусть каждому отрезку соответствует некоторое положительное
число так, что выполняются следующие условия:
1. Равным отрезкам соответствуют равные числа.
2. Если точка B лежит между точками А и С и отрезкам АВ
и ВС соответствуют числа a и b, то отрезку AC
соответствует число a+b.
3. Некоторому отрезку PQ соответствует число 1.
Тогда число, соответствующее отрезку, называется длиной этого
отрезка, а отрезок PQ называется единицей измерения.

59.

Процесс измерения
Примем отрезок CD в качестве единичного отрезка (единица
измерения). Будем измерять AB, используя отрезок CD. |CD|=1.
CD откладываем от точки A, получим AA1
An
A1
A2
Если A1 совпало с B, то |AB|=1
Если не совпало, то снова откладываем от точки A1 отрезок
A1A2 = СD
По аксиоме Архимеда число таких точек An будет конечно.
Возможны два случая:
1) An = B. Тогда |AB|= n

60.

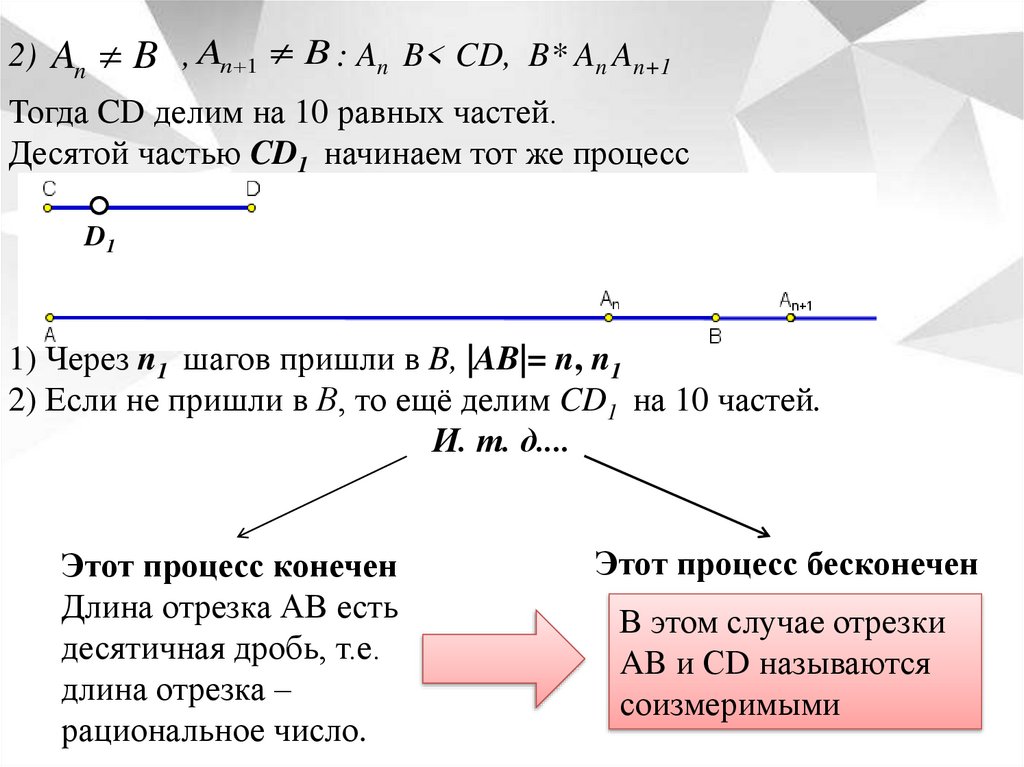
2) An B , An 1 B : An B< CD, B* An An+1
Тогда CD делим на 10 равных частей.
Десятой частью CD1 начинаем тот же процесс
D1
1) Через n1 шагов пришли в B, |AB|= n, n1
2) Если не пришли в В, то ещё делим CD1 на 10 частей.
И. т. д....
Этот процесс конечен
Длина отрезка АВ есть
десятичная дробь, т.е.
длина отрезка –
рациональное число.
Этот процесс бесконечен
В этом случае отрезки
AB и СD называются
соизмеримыми

61.

Процесс измерения бесконечен
В результате получим бесконечную последовательность
десятичных дробей: n
n,n1
n,n1n2
………….
В силу аксиомы Кантора эта последовательность должна сходится.
Предел этой последовательности будем называть длиной отрезка
|AB|. А это число будем называть иррациональным числом.
В этом случае отрезок AB и CD несоизмеримые.
Описанный нами процесс измерения одного отрезка другим
доказывает, что длина отрезка существует и обладает свойствами 1,
2,3 основного определения.

62.

Система координат
Можно ввести систему координат на прямой.
Пусть a – произвольная прямая. Точка O разбивает точки этой
прямой на два класса и прямую – на две полупрямые. Порядок
точек – слева направо. На прямой возьмем точку E1.
O E1 – единичный отрезок
I
II
O
Итак точка O(0) и точка O E1(1).
Таким образом мы установили
взаимно однозначное
соответствие между точками и
числами.
E1
a
P II : P( x) x | OP |
'
'
' x ' | OP ' |
P I : P (x )
Порядок точек на прямой и
порядок в поле действительных
чисел будет совпадать.
С помощью IV группы аксиом можно доказать, что для каждого
положительного числа существует отрезок, длина которого равна
этому положительному числу.

63.

Принцип Дедекинда
В теории действительного числа имеет место известный принцип
Дедекинда.
Т.к. система координат на прямой устанавливает взаимно
однозначное и взаимно непрерывное соответствие между точками
прямой и действительными числами, то для прямой имеет место
аналогичный принцип Дедекинда.
Каждая точка прямой разбивает множество всех точек прямой на 2
класса так, что каждый класс не пуст и каждая точка I класса будет
предшествовать каждой точке II класса
I
II
O
Точка O либо является последней точкой I класса, либо первой
точкой II класса.
Если принцип Дедекинда принять за аксиому, то аксиому Архимеда
и аксиому Кантора можно доказать. Т.е. эти утверждения
эквивалентны.

64.

V группа аксиом
Аксиома параллельных
Пусть а- произвольная прямая, А- произвольная точка вне
прямой а.
Тогда в плоскости α, определяемой прямой а и т.А,
существует не более одной прямой, проходящей через т.А и не
пересекающей прямую а.

65.

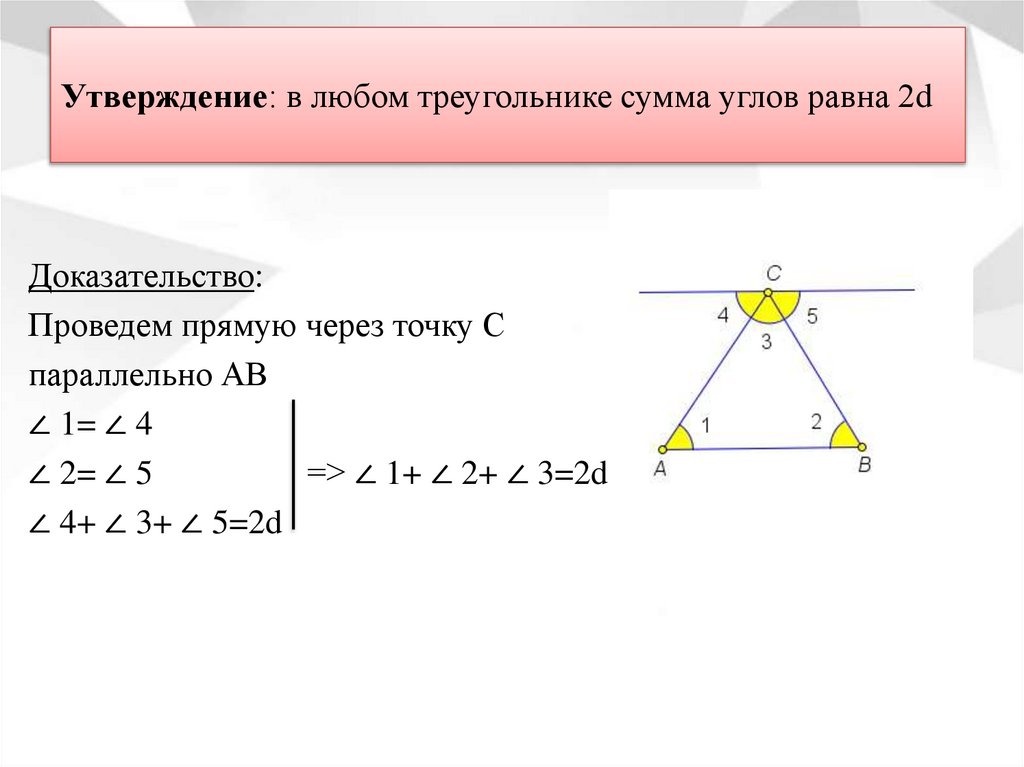
Утверждение: в любом треугольнике сумма углов равна 2d
Доказательство:
Проведем прямую через точку С
параллельно АВ
∠ 1= ∠ 4
∠ 2= ∠ 5
=˃ ∠ 1+ ∠ 2+ ∠ 3=2d
∠ 4+ ∠ 3+ ∠ 5=2d

66.

Теорема 11: если в треугольнике сумма углов 2d, то через точку
проходит одна прямая, параллельная данной.
Дано: сумма углов в любом треугольнике равна 2d.
Доказать: через точку проходит единственная прямая,
параллельная данной

67.

68.

69.

Замечание
Если ограничится аксиомами планиметрии, то III
группу аксиом можно заменить на аксиомы движения.
И получим ту же самую аксиоматику.
Аксиомы планиметрии
Аксиомы соединения
I1. Каковы бы не были 2 точки, существует прямая проходящая через эти
точки.
I2. Каковы бы не были 2 точки, существует не более 1 прямой, проходящей
через
I3. На каждой прямой лежат по крайней мере 2 точки. Существует по
крайней мере 3 точки, не лежащие на одной прямой.

70.

Аксиомы порядка
II1 Если точка B лежит между точками А и С , то А, B, C –три различные
точки прямой и B лежит между С и A
II2 Для любых 2-х точек A и B на прямой AB существует по крайней мере
одна точка С такая, что B лежит между А и С.
II3Среди любых трёх точек прямой существует не более одной точки,
лежащей между двумя другими.
II4. Аксиома Паша
Пусть A, B, C –три точки, не лежащие на одной прямой, и а –прямая, не
проходящая ни через одну из точек A,B,C. Если при этом прямая а проходит
через одну из точек отрезка AB, то она должна пройти через одну из точек
отрезка AC или через одну из точек отрезка BC.

71.

Аксиомы непрерывности
IV1 (аксиома Архимеда). Пусть AB и CD – произвольные отрезки. Тогда на
прямой AB существует конечное число точек A1, A2,… , An , расположенных
так, что точка A1 лежит между точками A и A2 , точка A2 лежит между A1 и
A3 и т.д., причем отрезки AA1, A1A2,… , An-1 An равны отрезку CD, а точка В
лежит между A и An .
n CD AB
IV2 (аксиома Кантора). Пусть на прямой а дана любая бесконечная
последовательность отрезков
A1B1, A2B2 ,…, из которых каждый последующий лежит внутри предыдущего,
и какой бы ни был отрезок, найдется n, что отрезок AnBn меньше этого
отрезка. Тогда существует точка X, лежащая внутри всех этих отрезков.

72.

Аксиома параллельных
Пусть а- произвольная прямая, А- произвольная точка вне прямой а.
Тогда существует не более одной прямой, проходящей через т.А и не
пересекающей прямую а.

73.

Аксиомы движения (наложения)
1. Наложение сопоставляет каждой точке точку, переводя
прямую в прямую, сохраняя при этом отношение
«лежать между» для трёх точек прямой.
2. Два последовательных наложения дают в результате
наложение и для всякого наложения найдётся обратное
ему наложение.
Совокупность Ф=(А,h,α) точки А, луча h с
началом в А и полуплоскости α,
ограниченной прямой, содержащей h
называется флагом.

74.

3. Для любых двух флагов Ф=(А,h,α) и существует
Ф ' ( A' , B ' , C ' ) единственное наложение,
переводящее Ф в Ф
Два отрезка называются равными, если существует
наложение, переводящий один отрезок в другой.
Аналогично для углов и других фигур.