Similar presentations:
Информатика. Описание графов
1.
Описание графов2.
Первая работа по теории графов1736 год
Санкт-Петербургская академия наук
Леонард Эйлер
Задача о кенигсбергских мостах –
"Можно ли, пройдя все городские мосты
ровно по одному разу, вернуться в
исходную точку?"
3.
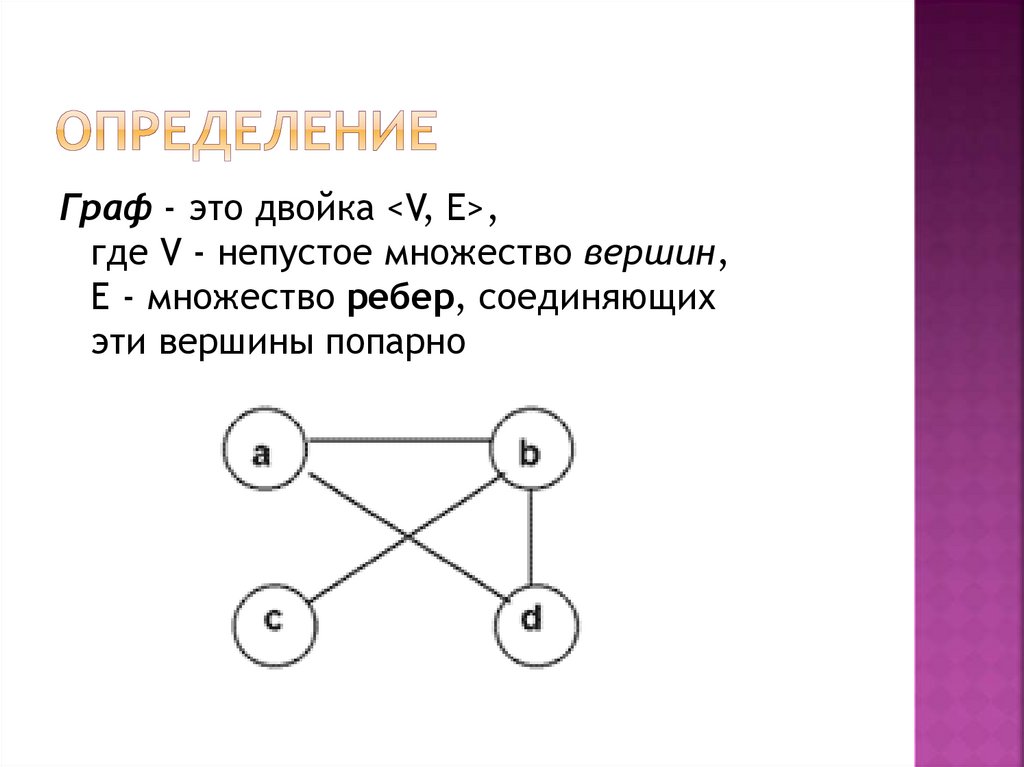
Граф - это двойка <V, E>,где V - непустое множество вершин,
Е - множество ребер, соединяющих
эти вершины попарно
4.
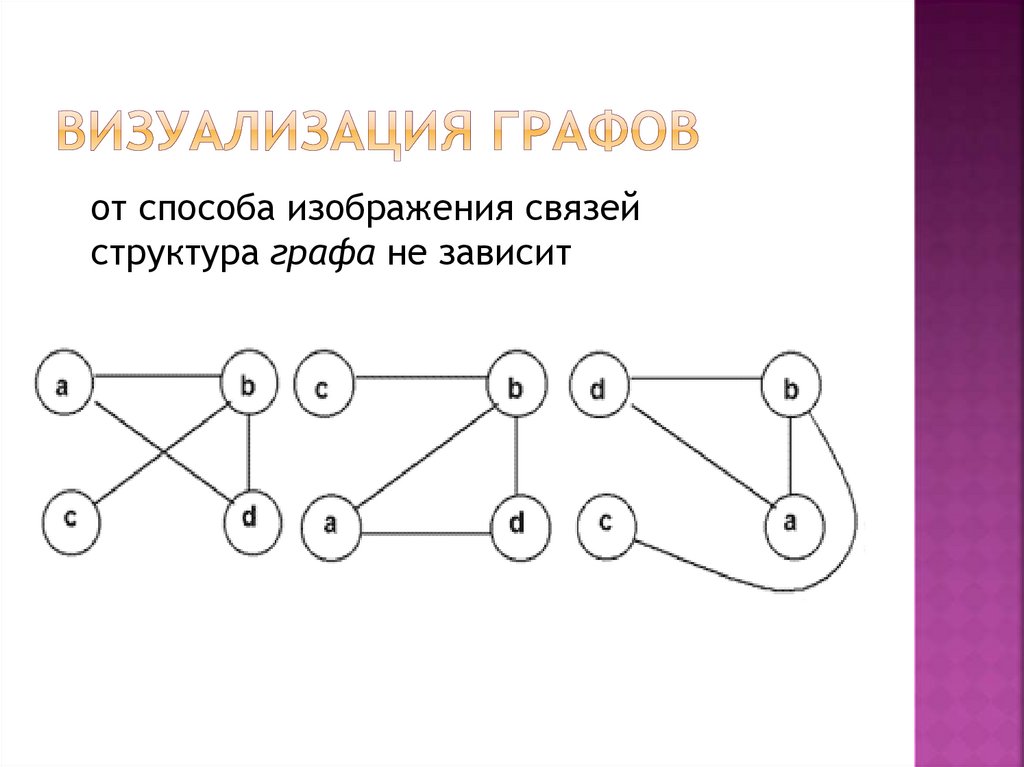
от способа изображения связейструктура графа не зависит
5.
ГрафВершины
Ребра
Семья
Люди
Родственные связи
Город
Перекрестки
Улицы
Сеть
Компьютеры
Кабели
Домино
Костяшки
Возможность
Дом
Квартиры
Соседство
Лабиринт
Развилки и тупики
Переходы
Метро
Станции
Пересадки
Листок в клеточку
Клеточки
Наличие общей границы
6.
НеориентированныеОриентированные
Взвешенные
7.
ребро – связь в обе сторонынет никакой разницы между "началом" и
"концом" ребра
8.
ГрафВершины
Ребра
Семья
Люди
Родственные связи
Город
Перекрестки
Улицы
Сеть
Компьютеры
Кабели
Домино
Костяшки
Возможность
Дом
Квартиры
Соседство
Лабиринт
Развилки и тупики
Переходы
Метро
Станции
Пересадки
Листок в клеточку
Клеточки
Наличие общей границы
9.
Ребро е и вершина v называются инцидентнымидруг другу, если вершина v является одним из
концов ребра е.
Две вершины называются смежными, если они
инцидентны одному ребру.
Аналогично, два ребра называются смежными,
если они инцидентны одной вершине.
Путь в графе - это последовательность вершин
(без повторений), в которой любые две соседние
вершины смежны.
Длина пути - количество ребер, из которых
этот путь состоит.
10.
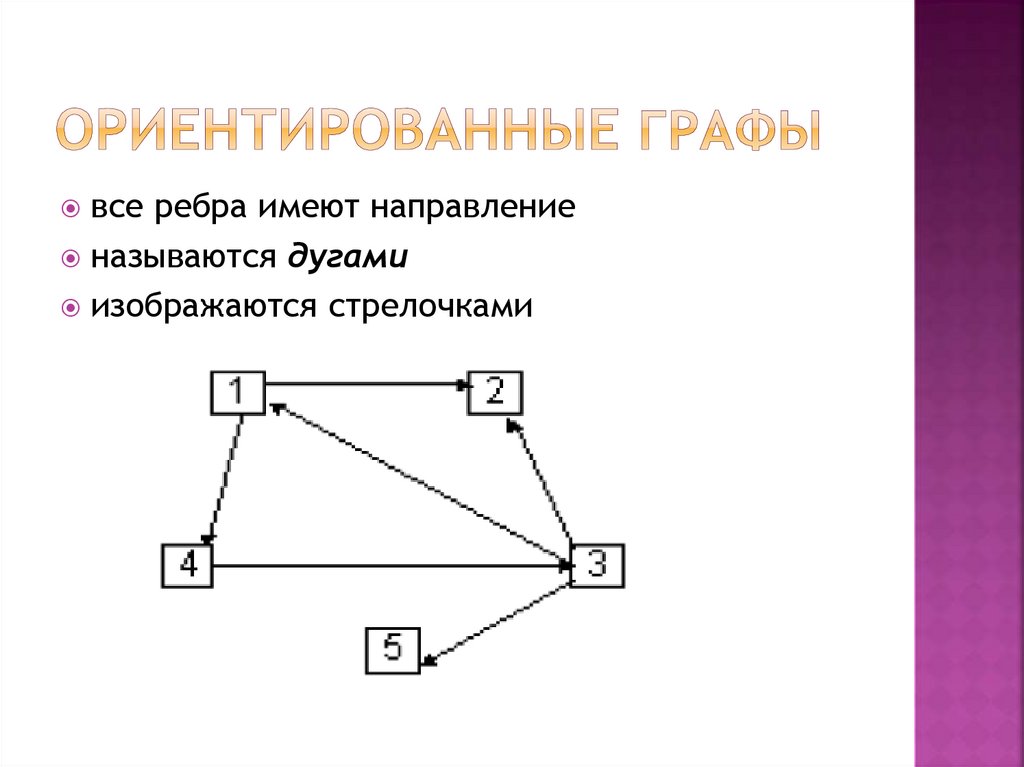
все ребра имеют направлениеназываются дугами
изображаются стрелочками
11.
ОрграфВершины
Дуги
Чайнворд
Слова
Совпадение последней и первой букв
(возможность связать два слова в цепочку)
Стройка
Работы
Необходимое предшествование (например,
стены нужно построить раньше, чем крышу,
т. п.)
Обучение
Курсы
Необходимое предшествование (например,
курс по языку Pascal полезно изучить
прежде, чем курс по Delphi, и т.п.)
Одевание
ребенка
Предметы
гардероба
Необходимое предшествование (например,
носки должны быть надеты раньше, чем
ботинки, и т.п.)
Европейский
город
Перекрестки
Узкие улицы с односторонним движением
Организация
Сотрудники
Иерархия (начальник - подчиненный)
12.
Путь в орграфе - это последовательностьвершин (без повторений), в которой любые две
соседние вершины смежны, причем
каждая вершина является одновременно концом
одной дуги и началом следующей дуги.
"Двигаться" по орграфу можно только в
направлениях, заданных стрелками.
13.
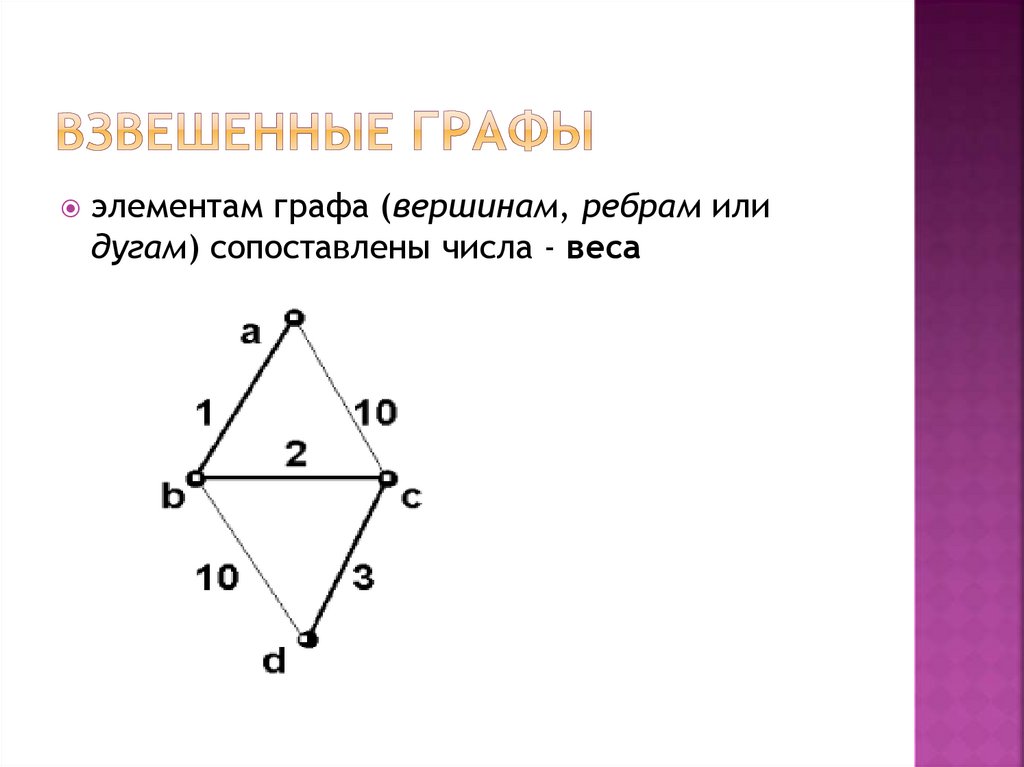
элементам графа (вершинам, ребрам илидугам) сопоставлены числа - веса
14.
ГрафВершины
Вес вершины
Ребра (дуги)
Вес ребра (дуги)
Таможни
Государства
Площадь
территории
Наличие
Стоимость
наземной границы получения визы
Переезды
Города
Стоимость
ночевки в
гостинице
Дороги
Суперчайнворд
Слова
-
Совпадение конца Длина
и начала
пересекающихся
слов(возможность частей
"сцепить" слова)
Карта
Государства
Цвет на карте
Наличие общей
границы
-
Сеть
Компьютеры -
Сетевой кабель
Стоимость
кабеля
Длина дороги
15.
Длина пути во взвешенном графе - это суммадлин (весов) всех ребер, из которых состоит
путь.
16.
Матрица смежностиСписок ребер
Списки смежности
Иерархический список
17.
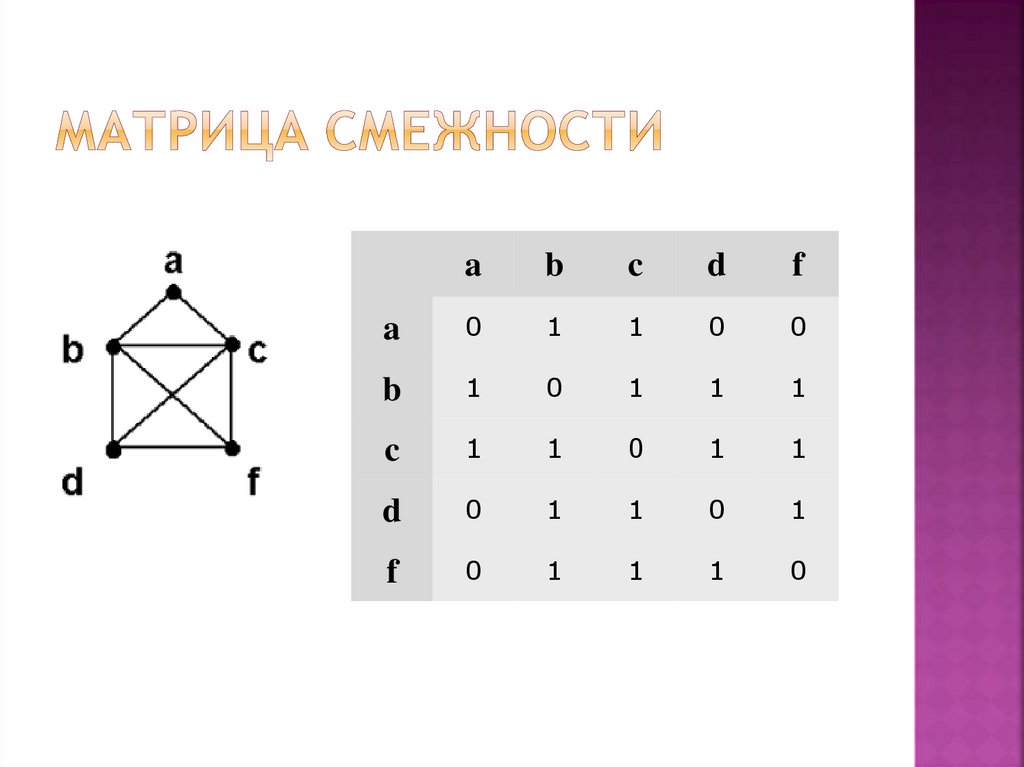
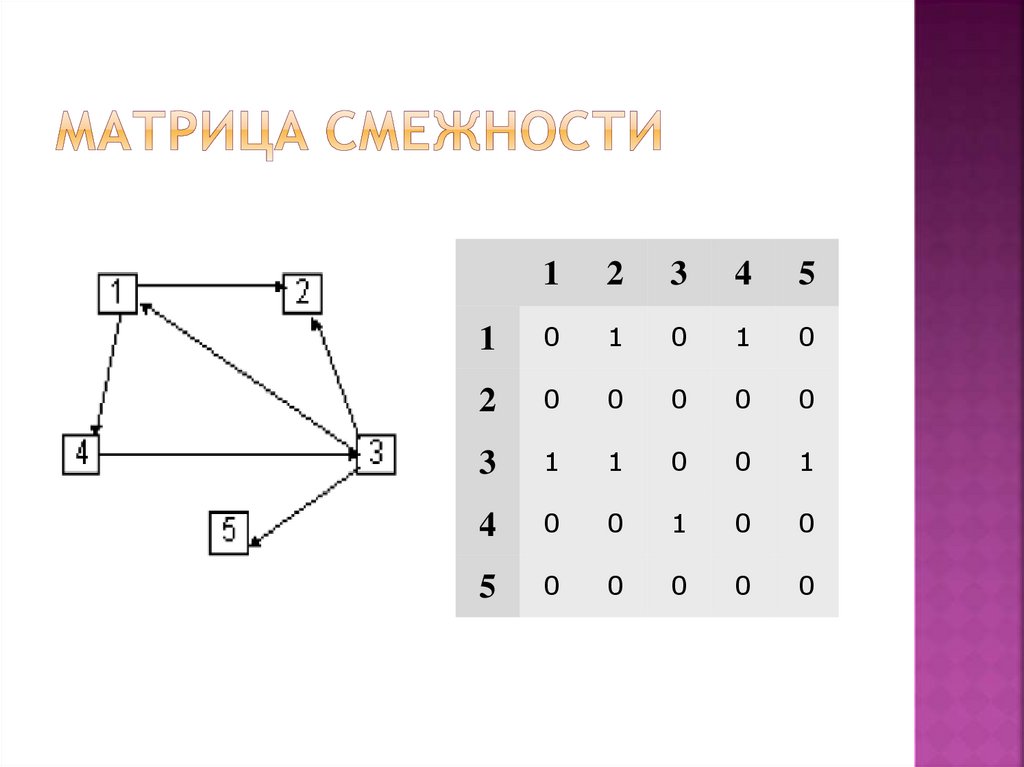
Матрица смежности Sm - это квадратнаяматрица размером NxN (N количество вершин в графе), заполненная
единицами и нулями по следующему
правилу:
Если в графе имеется ребро e,
соединяющее вершины u и v,
то Sm [u,v] = 1,
в противном случае Sm [u,v] = 0
18.
для неориентированного графасимметрична относительно своей главной
диагонали,
для орграфа - несимметрична
для взвешенного вместо 1 содержит
значения весов
19.
ab
c
d
f
a
0
1
1
0
0
b
1
0
1
1
1
c
1
1
0
1
1
d
0
1
1
0
1
f
0
1
1
1
0
20.
12
3
4
5
1
0
1
0
1
0
2
0
0
0
0
0
3
1
1
0
0
1
4
0
0
1
0
0
5
0
0
0
0
0
21.
ab
c
d
a
0
1
10
0
b
1
0
2
10
c
10
2
0
3
d
0
10
3
0
22.
+ наглядность и прозрачность алгоритмов,основанных на ее использовании
— избыточность данных: если граф далек от
полного, то матрица смежности, хранит
много "пустых мест" (нулей).
=> применяется для внутреннего
представления данных, а не для
пользовательского ввода
23.
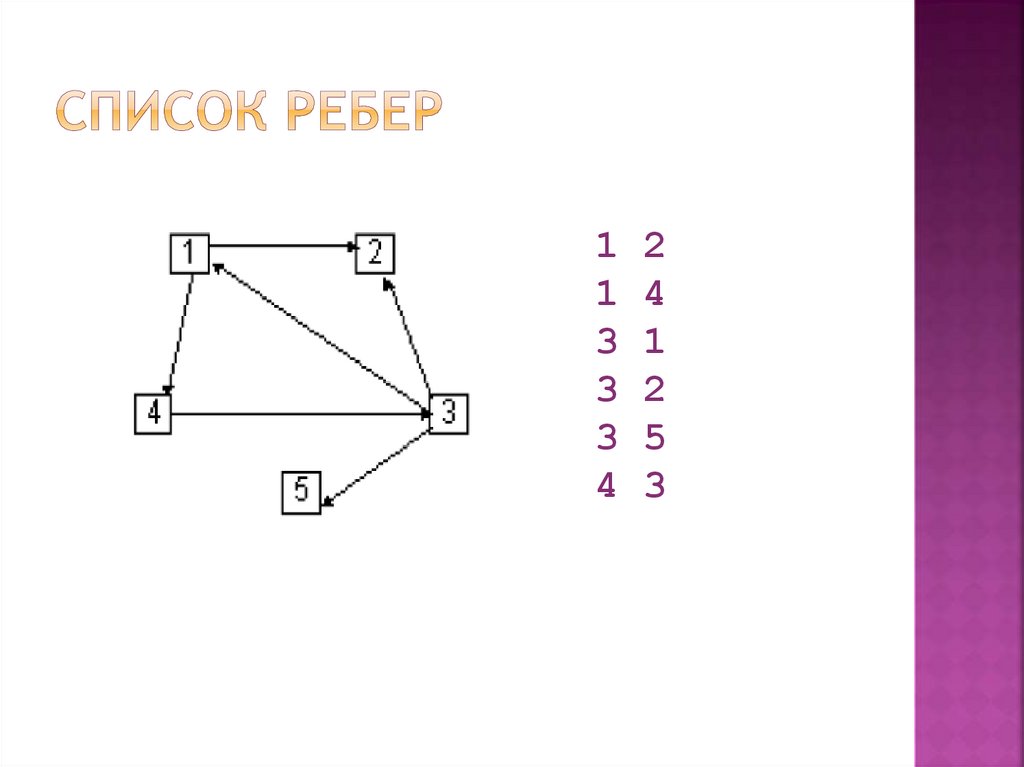
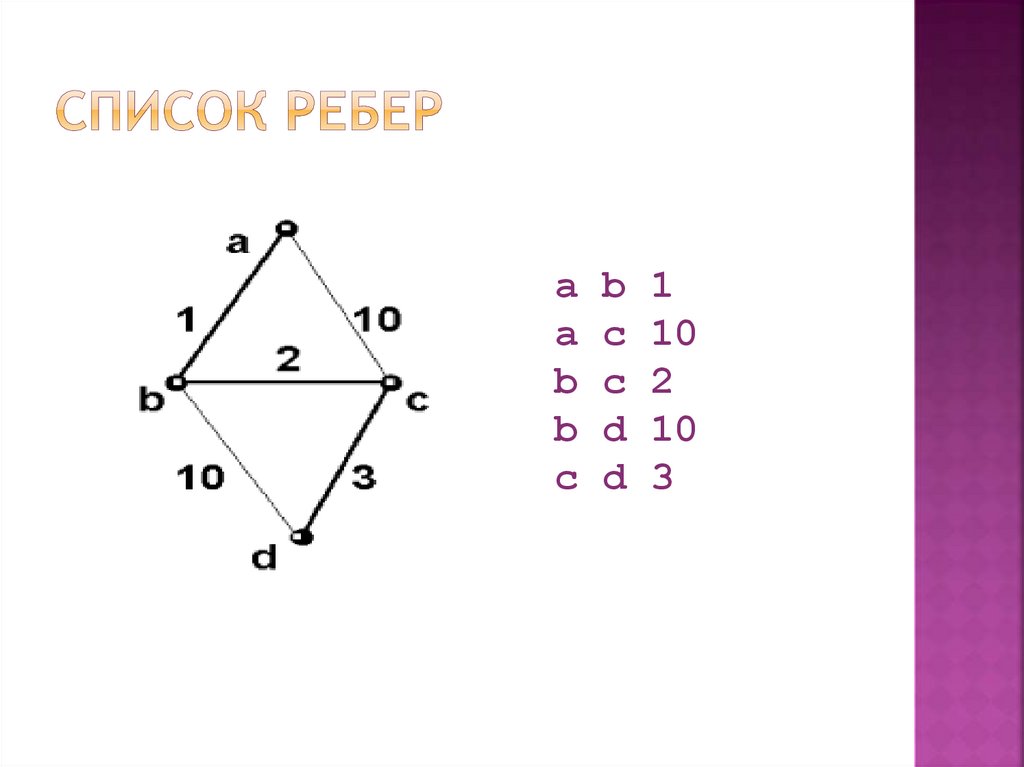
каждая строка списка ребер содержитинформацию об одном ребре (дуге):
<номер_начальной_вершины>
<номер_конечной_вершины>
[<вес_ребра>]
24.
для орграфа номера вершин понимаютсякак упорядоченная пара
если граф неориентированный - как
неупорядоченная
25.
a ba c
b c
b d
c d
c f
f d
b f
26.
1 21 4
3 1
3 2
3 5
4 3
27.
a b 1a c 10
b c 2
b d 10
c d 3
28.
+ неудобства в построении алгоритмов— неизбыточность данных
=> применяется для представления данных
пользователем
29.
для каждой вершины будет указан списоквсех смежных с нею вершин :
<номер_начальной_вершины>:
<номера_смежных_вершин>
Наиболее естественно применять этот
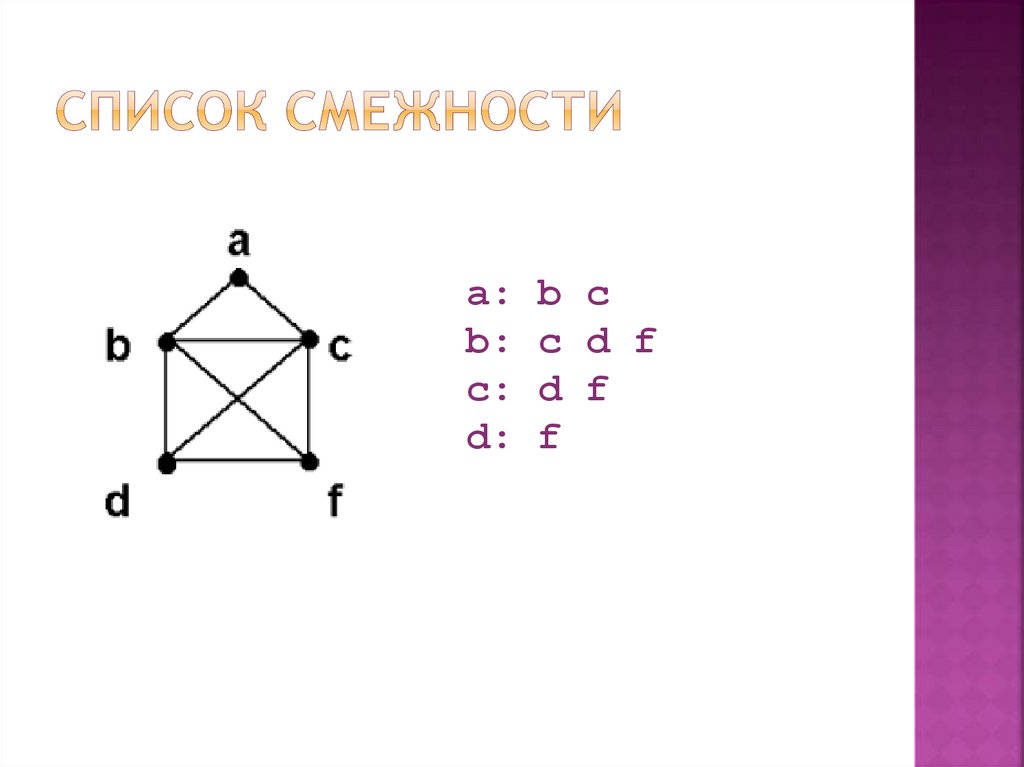
способ для задания орграфов, однако и
для остальных вариантов он тоже
подходит.
30.
a: b cb: c d f
c: d f
d: f
31.
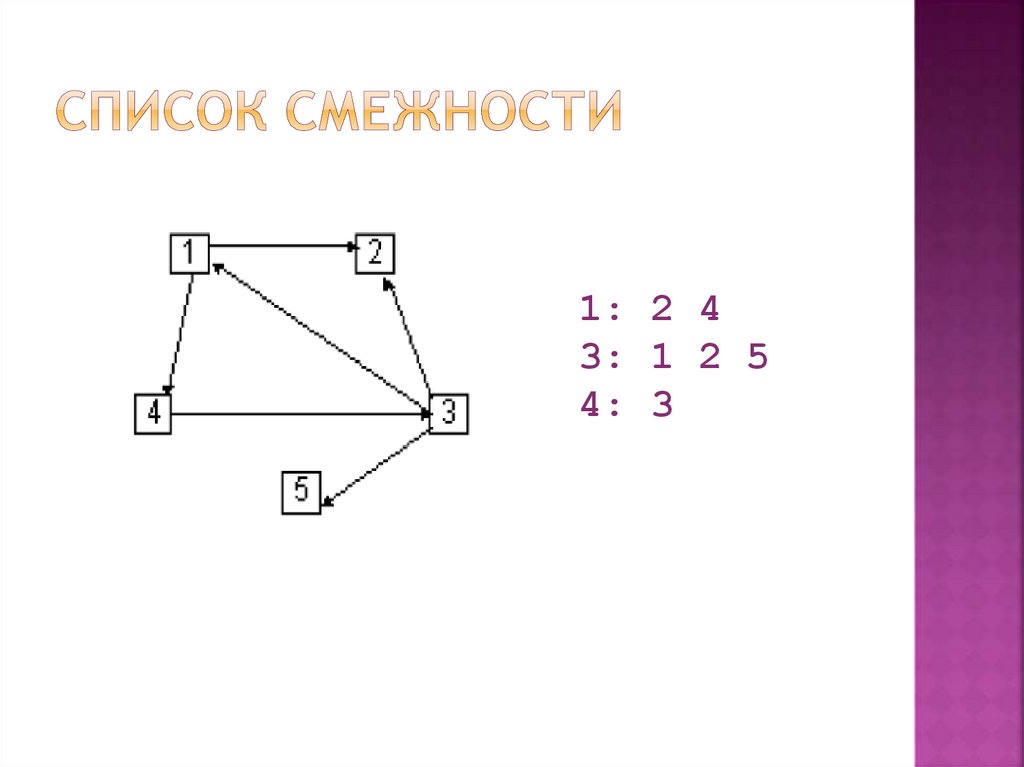
1: 2 43: 1 2 5
4: 3
32.
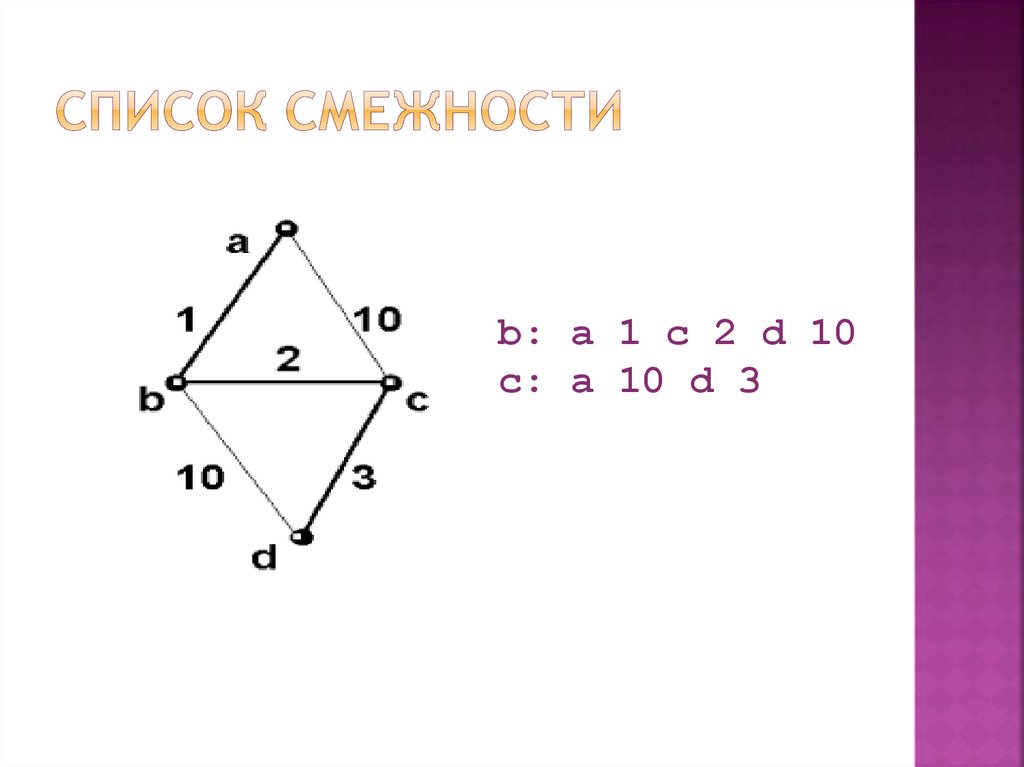
b: a 1 c 2 d 10c: a 10 d 3
33.
+ неудобства в построении алгоритмов— неизбыточность данных
=> применяется для представления данных
пользователем
34.
внутренняя реализация списка смежности:в одном линейном списке содержатся
номера "начальных вершин",
в остальных - номера смежных вершин или
указатели на эти вершины.
35.
36.
+ экономичное использование памяти+ удобства построения алгоритмов
=> применяется для программного
представления графов

























 informatics
informatics








