Виды систем счисления

1.

ВИДЫ СИСТЕМ
СЧИСЛЕНИЯ

2.

Система счисления (CC) - это совокупность правил и приемов
записи чисел с помощью набора цифровых знаков.
Основание системы счисления – это количество цифр,
необходимых для записи числа в системе.
Основание системы записывается справа от числа в нижнем
индексе:
32410
110012
AB516

3.

Различают два типа систем счисления:
– Позиционные, когда значение каждой цифры числа определяется
ее позицией в записи числа;
– Непозиционные, когда значение цифры в числе не зависит от ее
места в записи числа.
Примером непозиционной системы счисления является римская:
числа IX, IV, XV и т.д.
Примером позиционной системы счисления является десятичная
система, используемая повседневно.
Любое целое число в позиционной системе можно записать в
форме многочлена:
где S – основание системы счисления;
Xn– цифры числа, записанного в данной системе счисления;
n - количество разрядов числа.

4.

Позиционные системы
сотни десятки единицы
300
2 1 0
разряды
3 33
= 3·102 + 3·101 + 3·100
30
3
Другие позиционные системы:
• двоичная, восьмеричная, шестнадцатеричная (информатика)
• двенадцатеричная (1 фут = 12 дюймов, 1 шиллинг = 12 пенсов)
• двадцатеричная (1 франк = 20 су)
• шестидесятеричная (1 минута = 60 секунд, 1 час = 60 минут)
6

5.

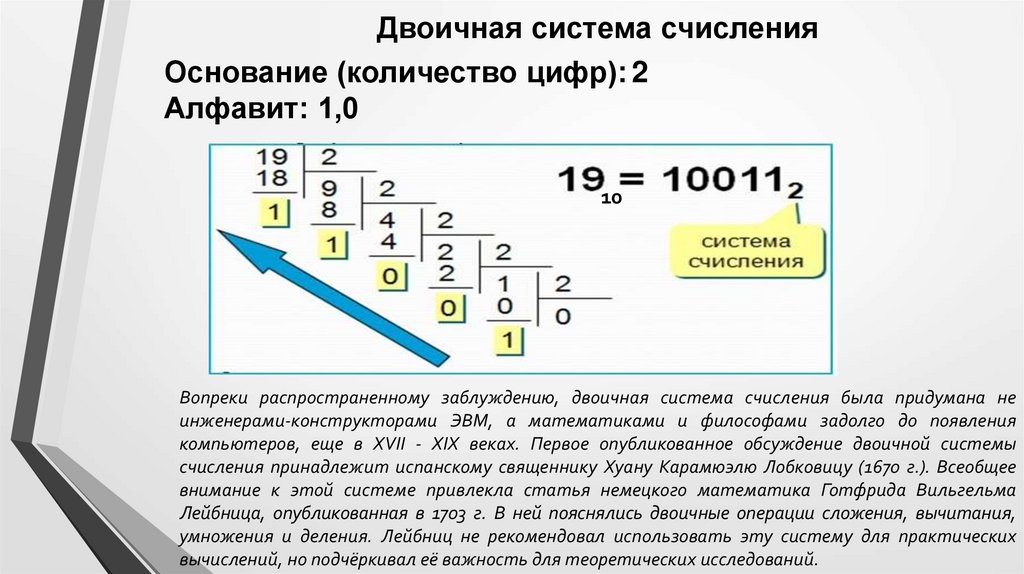
Двоичная система счисления
Основание (количество цифр): 2
Алфавит: 1,0
10
Вопреки распространенному заблуждению, двоичная система счисления была придумана не
инженерами-конструкторами ЭВМ, а математиками и философами задолго до появления
компьютеров, еще в ХVII - ХIХ веках. Первое опубликованное обсуждение двоичной системы
счисления принадлежит испанскому священнику Хуану Карамюэлю Лобковицу (1670 г.). Всеобщее
внимание к этой системе привлекла статья немецкого математика Готфрида Вильгельма
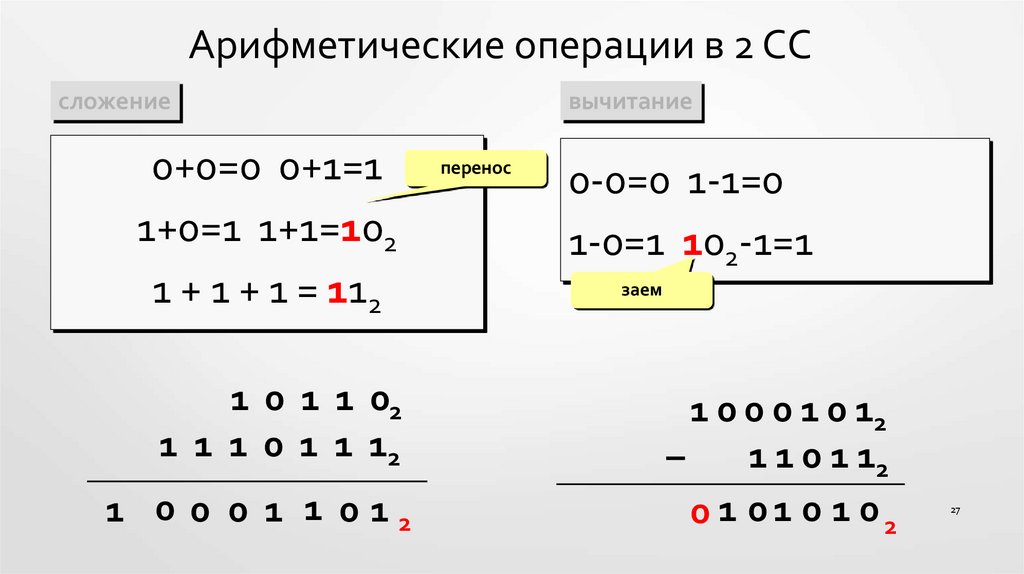
Лейбница, опубликованная в 1703 г. В ней пояснялись двоичные операции сложения, вычитания,
умножения и деления. Лейбниц не рекомендовал использовать эту систему для практических
вычислений, но подчёркивал её важность для теоретических исследований.

6.

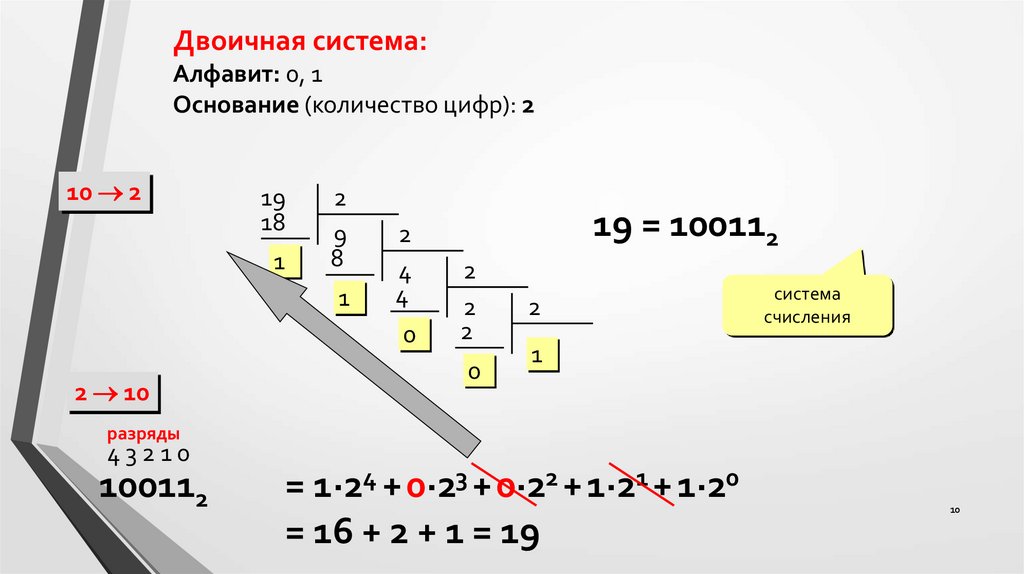
Двоичная система:
Алфавит: 0, 1
Основание (количество цифр): 2
10 2
19
18
1
2
9
8
1
2
4
4
0
2 10
19 = 100112
2
2
2
0
2
система
счисления
1
разряды
43210
100112
= 1·24 + 0·23 +0·22 + 1·21 + 1·20
= 16 + 2 + 1 = 19
10

7.

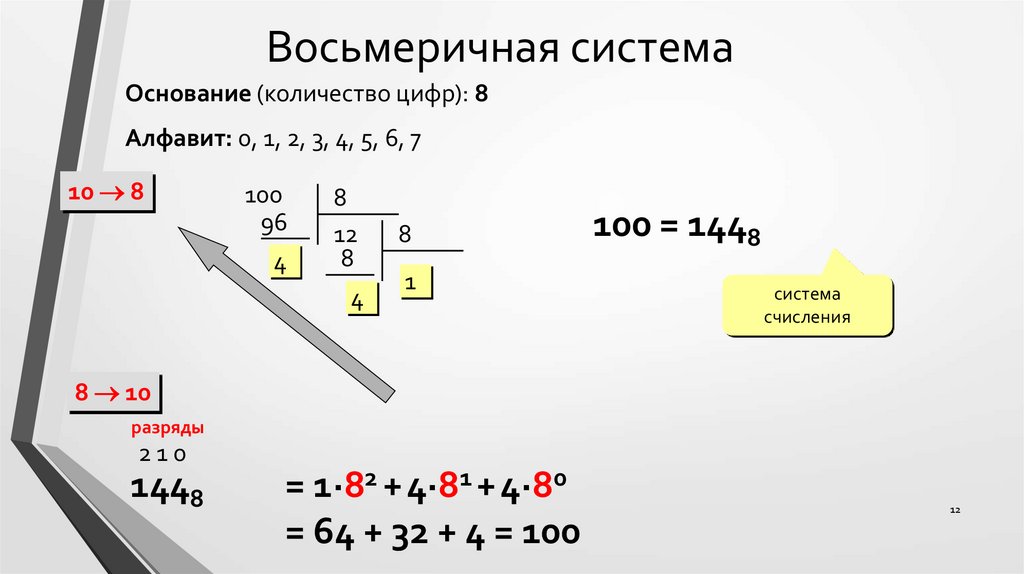
Восьмеричная система
Основание (количество цифр): 8
Алфавит: 0, 1, 2, 3, 4, 5, 6, 7
10 8
100
96
4
8
12
8
4
8
1
100 = 1448
система
счисления
8 10
разряды
210
1448
= 1·82 + 4·81 + 4·80
= 64 + 32 + 4 = 100
12

8.

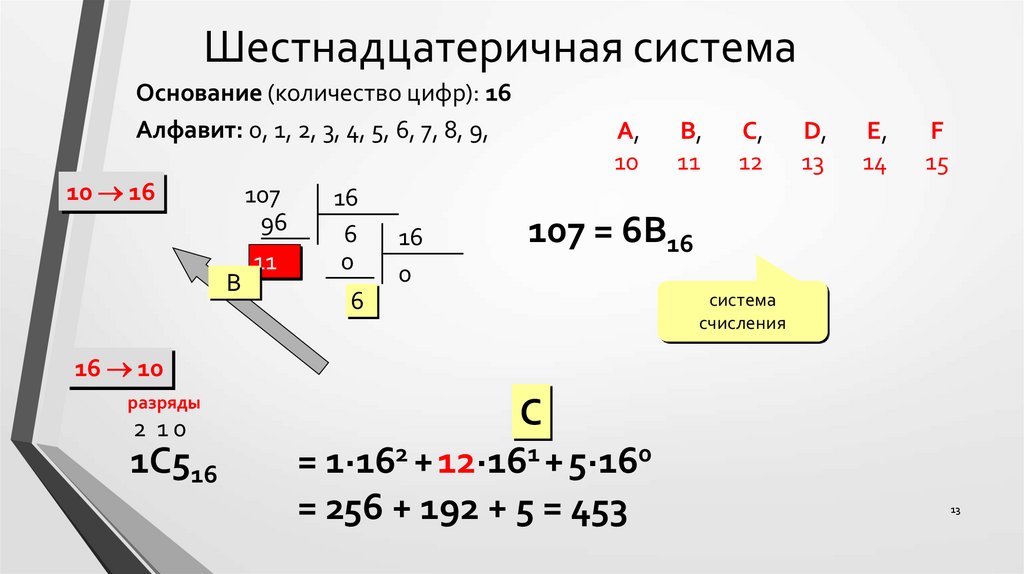
Шестнадцатеричная система
Основание (количество цифр): 16
Алфавит: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9,
10 16
107
96
B
11
16
6
0
16
0
A,
10
B,
11
C,
12
D,
13
E,
14
F
15
107 = 6B16
6
система
счисления
16 10
разряды
2 10
1C516
C
= 1·162 + 12·161 + 5·160
= 256 + 192 + 5 = 453
13

9.

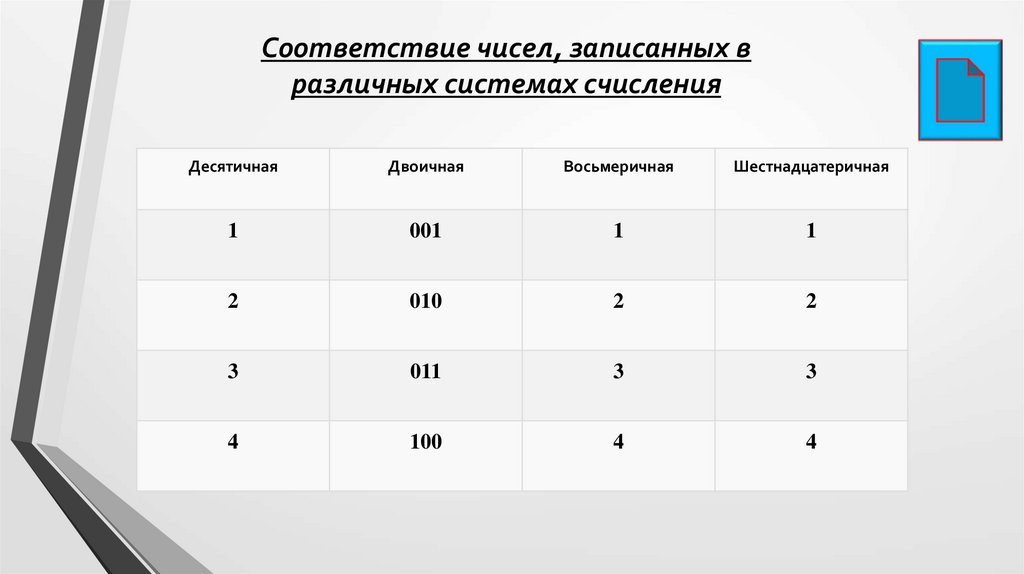
Соответствие чисел, записанных в
различных системах счисления
Десятичная
Двоичная
Восьмеричная
Шестнадцатеричная
1
001
1
1
2
010
2
2
3
011
3
3
4
100
4
4

10.

Правила перевода чисел из одной системы счисления в другую
Для перевода числа XS из системы с основанием S в десятичную систему счисления (X10) ,
его необходимо записать в виде многочлена, состоящего из произведений цифр числа и
соответствующей степени числа S, и вычислить по правилам десятичной арифметики: