Теория вероятностей. Основные понятия

1.

2. Теория вероятностей

Основные понятия

3. Этапы развития теории вероятностей

» 2-я половина XVI века – первые задачи
» по теории вероятностей.
Л.Пачоли
Д.Кардано
Н.Тарталья
Б.Паскаль
Я. Бернулли
А.Муавр
• Конец XVII- начало XIX века –
П.Лаплас
• формирование как самостоятельной
С.Пуассон
• научной дисциплины.
• Конец XIX – конец XX века –
• современный этап развития.
П.Л.Чебышёв
А.А.Марков
А.М.Ляпунов
А.Я.Хинчин
А.Н.Колмогоров

4. Основные понятия

• Стохастический эксперимент
• ( испытание, опыт) –
• - это такой эксперимент, результаты которого
заранее нельзя предугадать.
Примеры.
– 1. Бросание монеты;
– 2. Выстрел по мишени;
– 3. Бросание игральной кости (кубика);
– 4. Измерение физической величины (длины
изделия, влажности или температуры, давления)

5. Случайным называется явление,

которое при неоднократном воспроизведении одного и того
же опыта каждый раз может произойти по-иному.
Теория вероятностей - это наука,
занимающаяся изучением закономерностей в
массовых случайных явлениях.

6. Случайное событие –

- это факт, который может произойти или не
произойти в результате данного опыта.
Обозначения событий: A, B, C,…,ω,…
Пример 1. Бросание монеты.
Событие А - выпадение герба
Событие B - выпадение цифры

7. Пример 2. Бросание игральной кости

Событие А - выпадение четного числа очков.
Событие В - выпадение числа очков меньше, чем 4.
Событие С - выпадение шести очков.

8. Вероятность события - это

численная мера объективной возможности
появления данного события.
Обозначение: P(A) - вероятность события A

9. Невозможное и достоверное события

Невозможное событие – событие, которое
не может наступить в данном эксперименте.
(Обозначение Ǿ) .
Например, при бросании игральной кости не может
выпасть дробное число очков.
Достоверное событие – событие, которое
обязательно произойдет в данном
эксперименте. ( Ω)
Например, при бросании игральной кости - появление
целого числа очков.

10. Вероятность невозможного события равна 0.

Вероятность достоверного события равна 1.
Вероятность случайного события A:
0 P( A) 1

11. Несовместными называются события, которые не могут произойти одновременно в данном опыте.

Например, при одном бросании игральной кости не могут
одновременно выпасть 5 и 6 очков, эти случайные события
несовместны.

12. События называются равновозможными, если

ни одно из них не имеет большой возможности
появления, чем другие.
Например, появление герба и появление цифры при
бросании монеты.
Например, выпадение одного, двух, трех, четырех,
пяти и шести очков при бросании игрального
кубика - равновозможные события.

13. Несколько событий образуют полную группу,

если в результате испытания появится хотя бы одно
из них.
Пример: появление одного, двух, трех, четырех,
пяти и шести очков при бросании игрального
кубика - полная группа событий.

14. События, несовместные, равновозможные и образующие полную группу, называются случаями или исходами.

Случай называется благоприятствующим данному
событию, если появление этого случая влечет за
собой появление данного события.
Пример: событию A- появлению четного числа очков при
бросании игрального кубика благоприятствуют три случая
(исхода) - выпадет 2 очка, 4 очка и 6 очков.

15. Классическое определение вероятности

Вероятность случайного события A равна
отношению числа исходов, благоприятствующих
данному событию к общему числу исходов.
m
P( A)
n
n - число всех исходов испытания,
m - число исходов, благоприятствующих событию A.

16. Примеры

1. Какова вероятность, что при бросании одной
монеты выпадет герб?
Событие A -выпадет герб при бросании одной
монеты.
Общее число исходов n = 2.
Число исходов, благоприятствующих событию A:
m =1.
m 1
Значит
P( A)
n
2

17.

18.

19.

20.

21.

22. В формуле можно сократить на .

В формуле
Cnm
n!
можно сократить на (n m)! .
m!(n m)!
Cnm
Тогда получится
n!
n(n 1)(n 2) (n m 1)
m!(n m)!
1 2 3 m
n(n 1)(n 2) (n m 1)
C
1 2 3 m
m
n
Пример:
7 6
C
21
1 2
Если m
n
, то проще использовать формулу
2
2
7
C73
n m
n
C C
m
n
C75
7 6 5 4 3 7 6
C72
1 2 3 4 5 1 2
7 6 5
35
1 2 3

23. Пример

Нужно выбрать в подарок 4 из имеющихся 10-ти
разных книг. Сколькими способами это можно
сделать?
10 9 8 7
C
210
1 2 3 4
4
10

24.

25.

26. Размещениями из n элементов по m называются

комбинации (группы, наборы), составленные из
этих n элементов по m в каждой, отличающиеся
либо самими элементами, либо их порядком.
Число размещений:
n!
A
(n m)!
m
n

27. Число размещений из n элементов по m

n!
A
(n m)!
m
n
Можно сократить на
Anm
n!
n(n 1)(n 2)
(n m)!
(n m 1)
Anm n(n 1)(n 2) (n m 1)
Пример:
A72 7 6 42

28.

29.

30.

31.

32.

33.

34.

35. Пример 1

В приборе имеется 11 деталей, из них 3 неисправных.
Случайным образом выбирают 5 деталей. Какова
вероятность, что среди проверенных деталей окажутся
неисправными 2 детали?
Решение: Вычислим общее количество комбинаций из 11
5
462 , а количество благоприятных
деталей по 5 деталей: n C11
случаев равно m C32 C83 . Действительно, m m1 m2 ,
где m1 - количество способов выбрать из 8 исправных
деталей 3 детали, а m2 - количество способов выбрать из 3
неисправных деталей 2 детали. Имеем:
3 2
8 7 6
2
3 . Т.е. получим
m1 С83
56, m2 С3
1 2 3
1 2
P( A)
С32 С83
С115
3 2 8 7 6 5 168 4
1 2 1 2 3 4 462 11

36. Статистическое определение вероятности

• Пусть n – число повторений одного и того же
стохастического эксперимента.
• m(A) – число наступлений события А.
( A)
m( A)
относительная частота события А.
n
• Проводятся различные серии из n повторений одного и того
же стохастического эксперимента при n
• Определение.
• Событие А называется стохастически устойчивым,
• если ( A) p при n
• В этом случае Р(А)=р - это статистическое определение
вероятности.

37.

38.

39.

40. Частота события

• Пример. Бросание монеты.
• А=(выпадение герба).
• Бюффон (XVII век). n=4040, m(A)=2048.
( A) 0,507.
• К.Пирсон (конец XIX века). n=24000, m(A)=12012.
( A) 0,5005.
P(A)=0,5

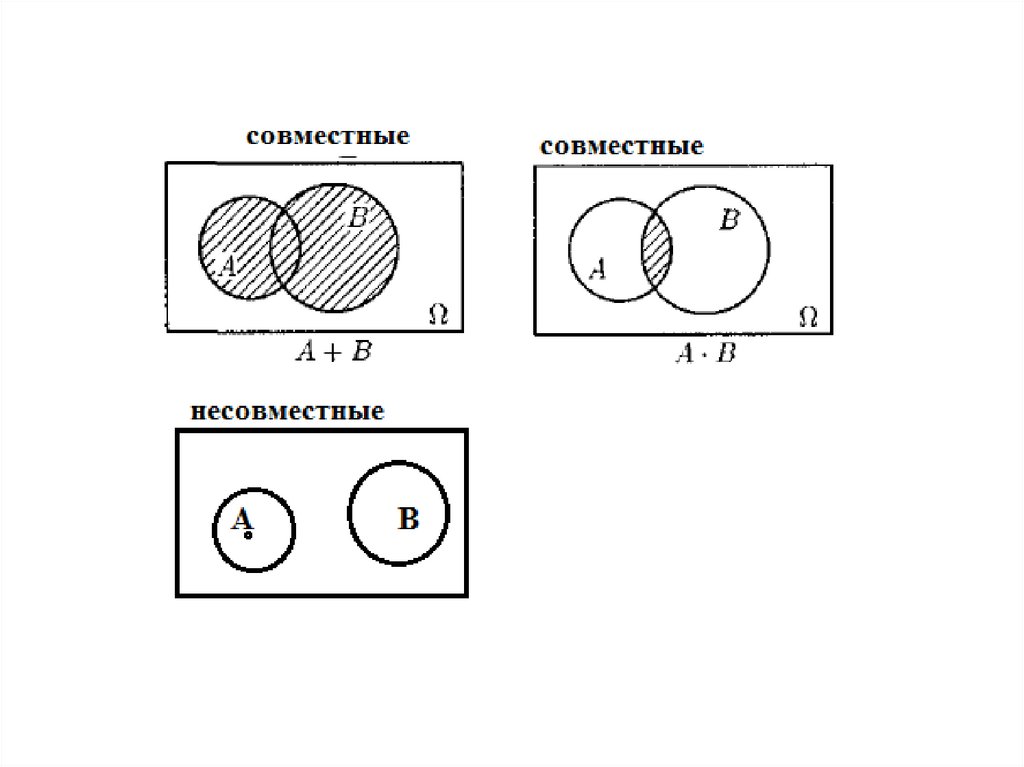
41. Геометрическое определение вероятности

• Пример.
• В квадрате случайным образом
выбирают точку (в квадрат случайным образом
бросают точку).
А
А =(точка попадает в круг А)
P( A)
S круга
S кв адрата

42. Геометрическое определение вероятности (продолжение)

• На фигуре Ф случайным образом выбирают точку
(любое положение точки равновозможно).
( ) мера фигуры.
• А=(точка попадает в область А).
( A) мера области А.
Ф
А
( A)
P( A)
( )

43. Пример.

На отрезок длины L наугад бросается точка. Какова
вероятность того, что она упадет не дальше, чем на
расстоянии m от середины отрезка.
• Решение.
Событие А: точка упадет не далее, чем на расстоянии m от середины,
т.е. точка попадает на отрезок длины 2m
2m
L
2m
P( A)
L
( 2m L)

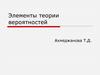
44. Сложение и умножение событий

• Сумма двух событий А и В – это такое
событие С=А+В, которое происходит, когда
наступает хотя бы одно из событий А или В.
• Произведение двух событий А и В – это такое
событие С=АВ, которое происходит, когда
наступают и А и В вместе.
Пример. Два стрелка делают по одному выстрелу в мишень.
Событие A - попадет первый, событие B - попадет второй.
A+B - попадет хотя бы один, т.е. или первый или второй
или оба вместе.
A B - попадут оба (первый и второй).

45.

46. Основные понятия

• Пример (диаграммы Венна).
• В квадрате случайным образом
выбирают точку (в квадрат случайным образом
бросают точку).
А
А =(точка попадает в круг А)

47. Основные понятия

В=(точка попадает в треугольник В)
А+В=(точка попадает хотя бы в одну фигуру А и В).
А
В

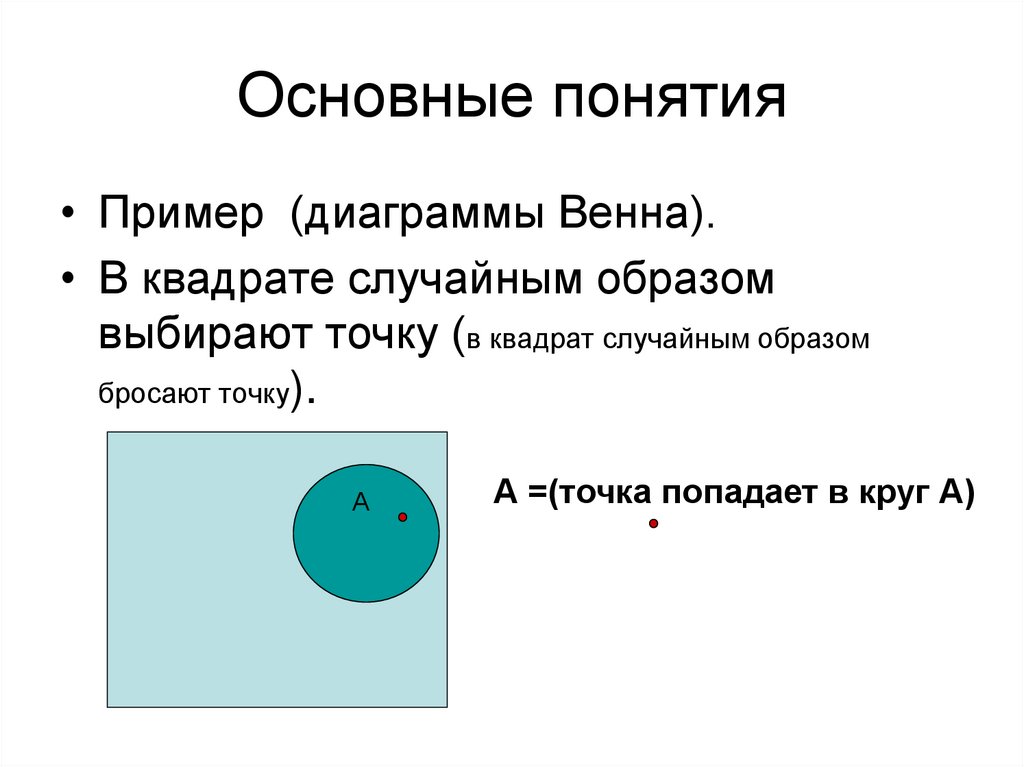
48. Основные понятия

АВ=(точка попадает в обе фигуры А и В).
A
В

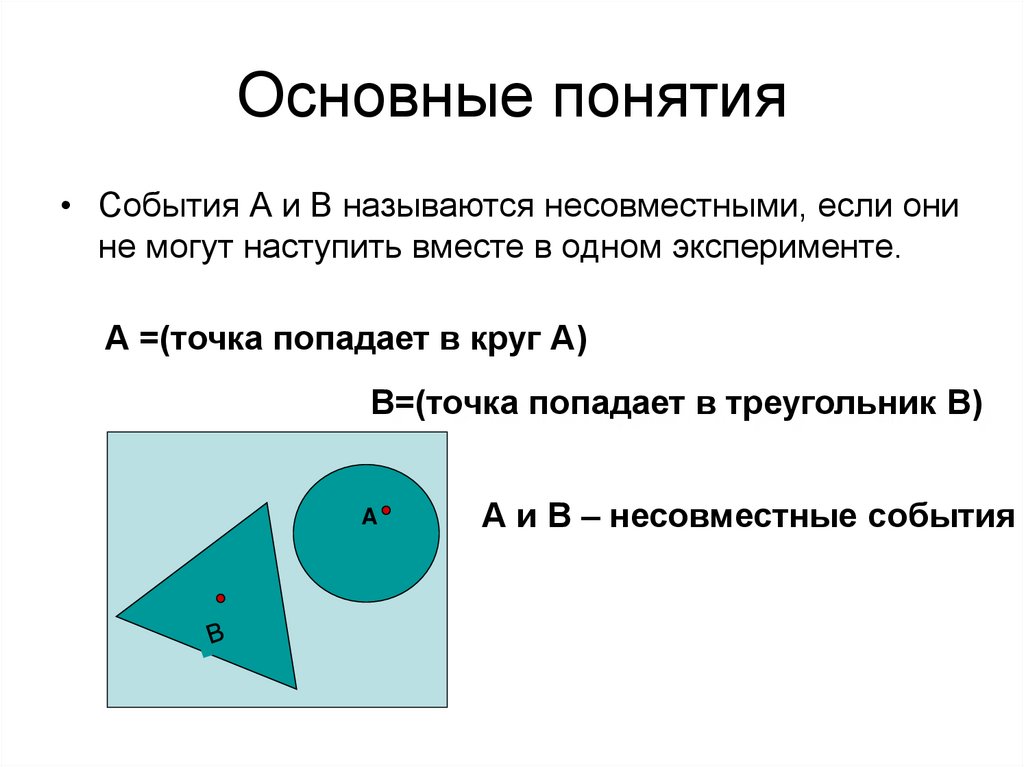
49. Основные понятия

• События А и В называются несовместными, если они
не могут наступить вместе в одном эксперименте.
А =(точка попадает в круг А)
В=(точка попадает в треугольник В)
A
А и В – несовместные события

50. Основные теоремы теории вероятностей

1. Теорема сложения вероятностей для несовместных
событий
Вероятность суммы двух несовместных событий равна
сумме вероятностей этих событий
P( A B) P( A) P( B)
Доказательство.
Пусть n – число всех исходов испытания,
m1 - число исходов, благоприятствующих событию А,
m2 - число исходов, благоприятствующих событию В,
тогда поскольку события A и B несовместны, событию A+B, т.е.
наступлению или A или B будет благоприятствовать m1 m2 исходов,
т.к. у событий A и B нет общих благоприятствующих исходов.
P( A B)
m m1 m2 m1 m2
P( A) P( B)
n
n
n
n

51.

52.

53. Пример

В лотерее 1000 билетов. Из них 1 билет - выигрыш 100 тыс.
рублей, 50 билетов по 5 тыс. рублей и 100 билетов по 1 тыс.
рублей. Какова вероятность выиграть по одному билету не
менее 5 тыс. рублей?
Решение. Событие C - выиграть по одному билету не менее 5
тыс. рублей.
A - выиграть 100 тыс. рублей, B - выиграть 5 тыс. рублей.
События A и B несовместны.
C=A+B
1
50
P(C ) P( A B) P( A) P( B)
0,051
1000 1000

54. Зависимые и независимые случайные события

Два события называются независимыми, если вероятность
появления одного не зависит от того, произошло второе или
нет.
Пример. Два стрелка делают по одному выстрелу в мишень. Событие
A - попадет первый, событие B - попадет второй. A и B - независимые
события.
Два события называются зависимыми, если вероятность
появления одного зависит от того, произошло второе или
нет.
Пример. В ящике имеется 20 шаров, из них 12 белых и 8 красных. Из
ящика берут наугад один шар и откладывают его в сторону. Событие
A- этот шар белый. Затем берут еще один шар. Событие B - второй
шар красный. Эти два события A и B зависимые.
1. Пусть событие A произошло, тогда в ящике осталось 11 белых и 8
PA ( B) что событие A
красных шаров. Вероятность события B при условии,
произошло обозначается так: P( B / A) или так
.

55. Умножение вероятностей

• Вероятность произведения двух независимых
• событий равна произведению их вероятностей.

56. 2. Теорема сложения вероятностей для совместных событий

Вероятность суммы двух совместных событий равна сумме
вероятностей этих событий без вероятности их совместного
появления.
P( A B) P( A) P( B) P( AB)
Доказательство.
Пусть n – число всех исходов испытания,
m1 - число исходов, благоприятствующих событию А,
m2 - число исходов, благоприятствующих событию В,
По условию события A и B совместны, значит у них есть общие
благоприятствующие исходы, обозначим число этих исходов mAB .
Число исходов, благоприятствующих событию A+B, будет
m m1 m2 mAB , т.к. в сумму m1 m2 исходы, благоприятствующие
совместному появлению A и B входят дважды. Тогда
P( A B)
m1 m2 mAB m1 m2 mAB
P( A) P( B) P( AB)
n
n
n
n

57.

58. Пример

Два стрелка делают по одному выстрелу в мишень.
Вероятность попадания первого равна 0,8, а второго - 0,7.
Найти вероятность того, что мишень будет поражена, т.е. что
попадет хотя бы один стрелок.
Решение. Пусть событие C - попадет хотя бы один стрелок,
C = A + B.
Событие A - попадет первый, P(A) = 0,8,
событие B - попадет второй, P(B) = 0,7.
A и B совместны ( могут произойти вместе) . Тогда
P(C) P( A B) P( A) P( B) P( AB) 0,8 0,7 0,8 0,7 0,94

59.

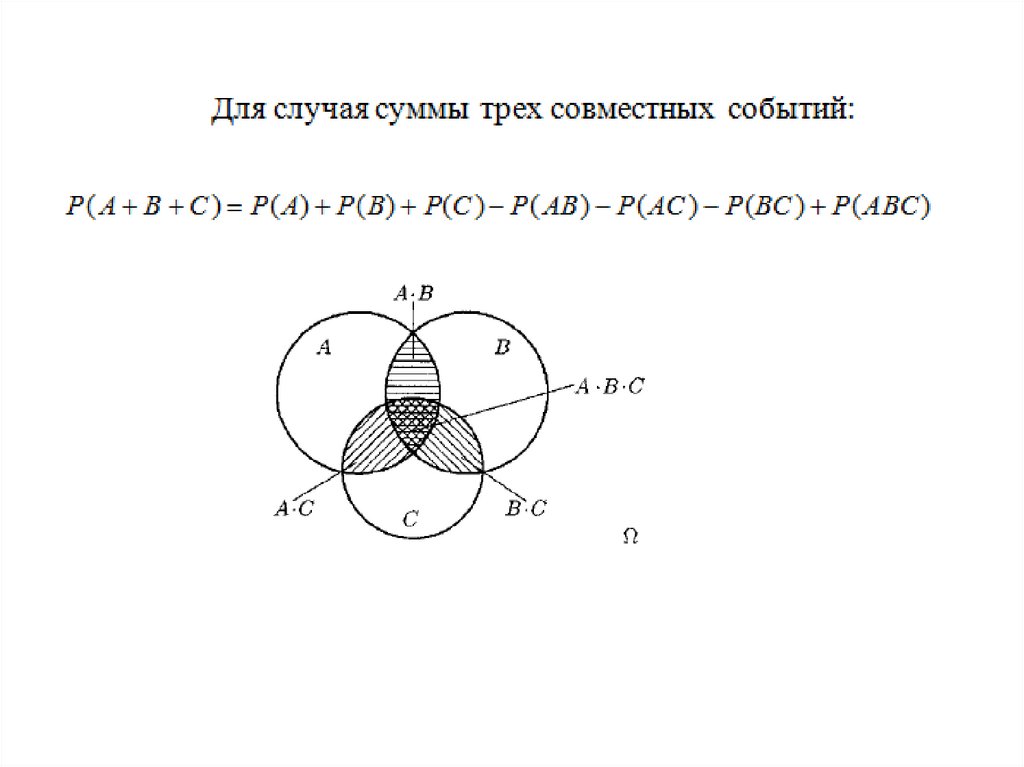
60. Для случая суммы трех совместных событий:

P( A B C) P( A) P( B) P(C) P( AB) P( AC) P(BC) P( ABC)
Еще более громоздкой будет формула для вероятности
суммы четырех совместных событий.
Есть более рациональный способ вычисления - это переход к
противоположному событию (рассмотрим на следующих
слайдах).

61. Противоположные события

Два несовместных события, образующих полную группу,
называются противоположными.
Они обозначаются A и A .
- достоверное событие.
A A ,
P( A) P( A) 1
P( A) 1 P( A)
Пример. A - попадание в цель, P(A) = 0,9
A - промах,
P( A) 1 P( A) 1 0,9 0,1 .

62. То есть событию: хотя бы один противоположно событие: ни один. Если нужно найти вероятность суммы трех или более совместных

событий, то более рациональным решением будет переход к
противоположному событию, как в предыдущем примере.

63. 2). Брошены монета и игральный кубик. Какова вероятность, что выпадет герб и шесть очков?

Ответ:
1
.
12
3). В студии телевидения 3 телекамеры.
Для каждой камеры вероятность того, что она
включена в данный момент, равна 0,6. Найти
вероятность того, что в данный момент
включена хотя бы одна камера.

64. Решение.

А – включена первая телекамера,
В – включена вторая телекамера,
С – включена третья телекамера, A, B, C - совместные события
D – включена хотя бы одна телекамера, D = A + B + C
D - все телекамеры выключены (это событие
противоположное D).
Тогда D A B C и
P( D) P(A) P( B) P( C) 0,43 0,064
P(D) 1 P( D) 1 0,064 0,936

65. Примеры.

• 1). Определить надежность (вероятность
безотказной работы за время Т) схемы,
составленной из двух последовательно
соединенных элементов А и В, если
надежность этих элементов соответственно
равна p1 и p 2 .

66.

67.

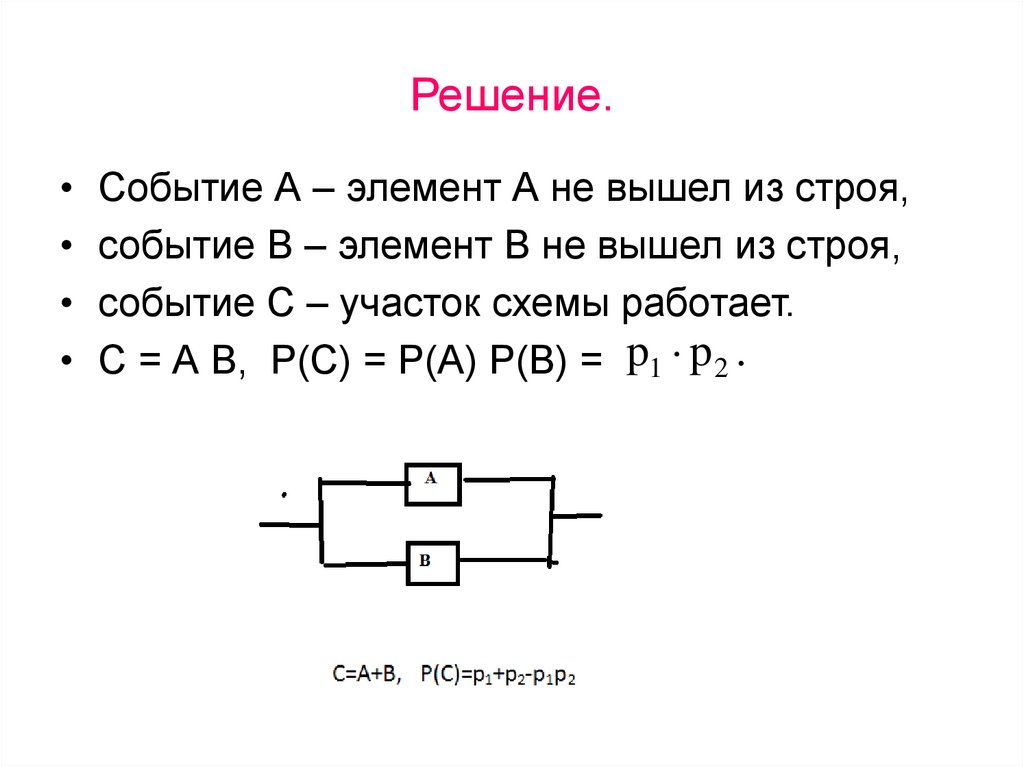
68. Решение.

• Событие А – элемент А не вышел из строя,
• событие В – элемент В не вышел из строя,
• событие С – участок схемы работает.
• С = А В, Р(С) = Р(А) Р(В) = p1 p 2 .