Обработка систематических погрешностей. Лекция 3

1.

Лекция 3
Обработка систематических
погрешностей

2.

Лекция 3. Обработка систематических погрешностей
X i Q i i – результат измерения, Q – истинное значение физической величины,
Δi – i-ая случайная погрешность, Θi – i-ая систематическая погрешность;
1 n
1 n
1 n
X X i Q i i – усреднение по n измерениям;
n i 1
n i 1
n i 1
1 n
1 n
i
0, i
n
n
n i 1
n i 1
X Q
Неисправленные результаты – результаты наблюдений, полученные при
наличии систематической погрешности.
2

3.

Лекция 3. Обработка систематических погрешностей
СПОСОБЫ УСТРАНЕНИЯ ПОСТОЯННЫХ
СИСТЕМАТИЧЕСКИХ ПОГРЕШНОСТЕЙ
Устранение
источников
погрешностей до
начала измерений
Определение
поправок и внесение
их в результат
измерения
Оценка границ
неисключенных
систематических
погрешностей
3

4.

Лекция 3. Обработка систематических погрешностей
СПОСОБЫ УСТРАНЕНИЯ ПОСТОЯННЫХ
СИСТЕМАТИЧЕСКИХ ПОГРЕШНОСТЕЙ
Устранение источников погрешностей до начала измерений
Метод замещения
Метод
противопоставления
Метод компенсации
по знаку
Метод
рандомизации
4

5.

Лекция 3. Обработка систематических погрешностей
СПОСОБЫ УСТРАНЕНИЯ ПОСТОЯННЫХ
СИСТЕМАТИЧЕСКИХ ПОГРЕШНОСТЕЙ
Устранение источников погрешностей до начала измерений
1. На чашу весов помещают взвешиваемое тело
массой mx и отмечают положение указателя N;
2. Взвешиваемое тело замещают гирями такой
массы m0, чтобы вновь добиться прежнего
отклонения указателя N;
3. При одинаковых отклонениях указателя будет
выполняться условие mx = m0
Метод замещения
на пружинных весах
5

6.

Лекция 3. Обработка систематических погрешностей
СПОСОБЫ УСТРАНЕНИЯ ПОСТОЯННЫХ
СИСТЕМАТИЧЕСКИХ ПОГРЕШНОСТЕЙ
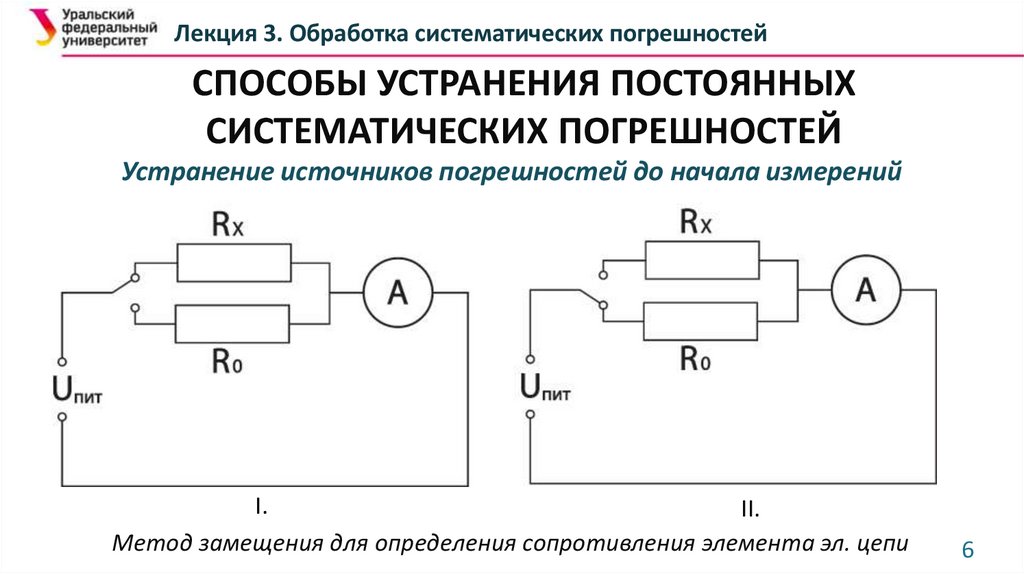
Устранение источников погрешностей до начала измерений
I.
II.
Метод замещения для определения сопротивления элемента эл. цепи
6

7.

Лекция 3. Обработка систематических погрешностей
СПОСОБЫ УСТРАНЕНИЯ ПОСТОЯННЫХ
СИСТЕМАТИЧЕСКИХ ПОГРЕШНОСТЕЙ
Устранение источников погрешностей до начала измерений
f0
1
LC
– частота LC-контура;
I.
II.
Метод замещения для определения емкости и индуктивности эл. цепи
7

8.

Лекция 3. Обработка систематических погрешностей
СПОСОБЫ УСТРАНЕНИЯ ПОСТОЯННЫХ
СИСТЕМАТИЧЕСКИХ ПОГРЕШНОСТЕЙ
Устранение источников погрешностей до начала измерений
l1
mx m0
― выражение для нахождения неизвестной массы;
l2
1. Взвешивают груз mx, уравновешивая его гирями
массой m01. При этом справедливо mx · l1 = m01 · l2 ;
2. Затем груз mx перемещают на вторую чашу весов,
уравновешивая его гирями массой m02. При этом
справедливо mx · l2 = m02 · l1 ;
3. Из двух соотношений условий равновесия весов
находим выражение для неизвестной массы:
Метод противопоставления
(равноплечные весы)
mx m01 m02
8

9.

Лекция 3. Обработка систематических погрешностей
СПОСОБЫ УСТРАНЕНИЯ ПОСТОЯННЫХ
СИСТЕМАТИЧЕСКИХ ПОГРЕШНОСТЕЙ
Устранение источников погрешностей до начала измерений
I.
1 R3
Rx R2
R1
2 R1
II. Rx R2
R3
III. Rx
I.
II.
Метод противопоставления (измерительный мост)
R21 R22
9

10.

Лекция 3. Обработка систематических погрешностей
СПОСОБЫ УСТРАНЕНИЯ ПОСТОЯННЫХ
СИСТЕМАТИЧЕСКИХ ПОГРЕШНОСТЕЙ
Устранение источников погрешностей до начала измерений
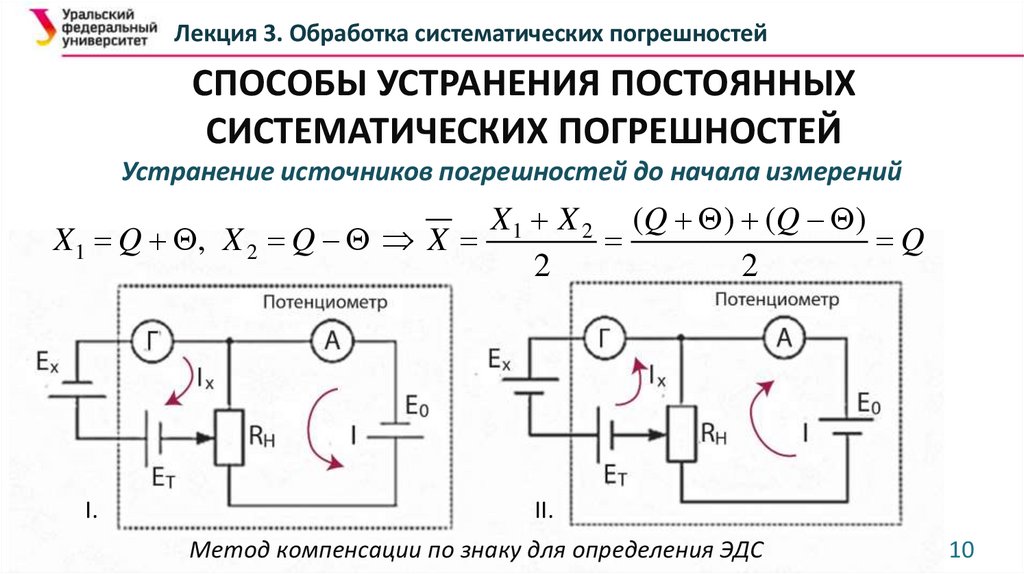
X 1 X 2 (Q ) (Q )
X 1 Q , X 2 Q X
Q
2
2
I.
II.
Метод компенсации по знаку для определения ЭДС
10

11.

Лекция 3. Обработка систематических погрешностей
СПОСОБЫ УСТРАНЕНИЯ ПОСТОЯННЫХ
СИСТЕМАТИЧЕСКИХ ПОГРЕШНОСТЕЙ
Метод рандомизации
…
1
2
X ( P) t p z p
SХ
;
n
3
n
X X X ( P), P Р%, n.
11

12.

Лекция 3. Обработка систематических погрешностей
СПОСОБЫ УСТРАНЕНИЯ ПОСТОЯННЫХ
СИСТЕМАТИЧЕСКИХ ПОГРЕШНОСТЕЙ
Определение поправок и внесение их в результат измерения
Поправка – значение величины, вводимое в неисправленный результат
измерения с целью исключения составляющих систематической погрешности. Численно
равно абсолютной погрешности, взятой с обратным знаком.
X̂ X X , X 0, 01X – значение измеренной
величины при нормальной температуре;
T
– дополнительная погрешность, возникающая при
Х доп X
1
Tнорм отклонении нормального значения температуры более
чем на 5 °С;
Xˆ X X X доп – итоговый результат с учетом поправки.
12

13.

Лекция 3. Обработка систематических погрешностей
СПОСОБЫ УСТРАНЕНИЯ ПОСТОЯННЫХ
СИСТЕМАТИЧЕСКИХ ПОГРЕШНОСТЕЙ
Определение поправок и внесение их в результат измерения
Устранение систематической погрешности путем введения поправки
13

14.

Лекция 3. Обработка систематических погрешностей
СПОСОБЫ УСТРАНЕНИЯ ПОСТОЯННЫХ
СИСТЕМАТИЧЕСКИХ ПОГРЕШНОСТЕЙ
Определение поправок и внесение их в результат измерения
Q X tP S X
– неисправленное значение измеряемой величины;
С t P SC – значение поправки;
Q ' ( X С t P SC ) t P S X X ' t P S S – исправленный результат;
S S SC2 S X2
– СКО исправленного результата;
D1 1 t P S X ,
D2 2 t P SC 1 C t P SC2 S X2
предельные значения погрешностей
до и после введения поправки.
14

15.

Лекция 3. Обработка систематических погрешностей
СПОСОБЫ УСТРАНЕНИЯ ПОСТОЯННЫХ
СИСТЕМАТИЧЕСКИХ ПОГРЕШНОСТЕЙ
Определение поправок и внесение их в результат измерения
Целесообразность введения поправки:
D1 D2
1 t P S X 1 C t P SC2 S X2 , C t P SC2 S X2 t P S X
S2
C
C tP S X
1 1
2
S
X
SC2
0,5 2 , SC
S
X
SX
Вывод: если S C 0 , то поправку имеет смысл вводить всегда.
15

16.

Лекция 3. Обработка систематических погрешностей
СПОСОБЫ УСТРАНЕНИЯ ПОСТОЯННЫХ
СИСТЕМАТИЧЕСКИХ ПОГРЕШНОСТЕЙ
Определение поправок и внесение их в результат измерения
Поверка средства измерений – совокупность операций, выполняемых в
целях подтверждения соответствия средств измерений установленным для них
обязательным, в том числе метрологическим, требованиям (ГОСТ Р 8.973-2019).
Калибровка средства измерения – совокупность операций, выполняемых в
целях определения действительных значений метрологических характеристик средств
измерений (ГОСТ Р 8.879-2014).
Постановление Правительства Российской Федерации от 20 апреля 2010 г. № 250 «О перечне
средств измерений, поверка которых осуществляется только аккредитованными в установленном
порядке в области обеспечения единства измерений государственными региональными центрами
метрологии».
16

17.

Лекция 3. Обработка систематических погрешностей
СПОСОБЫ УСТРАНЕНИЯ ПОСТОЯННЫХ
СИСТЕМАТИЧЕСКИХ ПОГРЕШНОСТЕЙ
Оценка границ неисключенных систематических погрешностей
Неисключенная систематическая погрешность (неисключенный остаток
систематической погрешности) – составляющая погрешности результата измерений,
обусловленная погрешностями вычисления и введения поправок на влияние
систематических погрешностей или систематической погрешностью, поправка на
действие которой не введена вследствие ее малости.
N
i , N 3
i 1
– границы неисключенной систематической погрешности.
N
K
2
i , N 3
i 1
17

18.

Лекция 3. Обработка систематических погрешностей
СПОСОБЫ УСТРАНЕНИЯ ПОСТОЯННЫХ
СИСТЕМАТИЧЕСКИХ ПОГРЕШНОСТЕЙ
Оценка границ неисключенных систематических погрешностей
/ S X 0,8
/ SX 8
0,8 / S X 8
пренебрегают неисключенной
систематической погрешностью
пренебрегают случайной
погрешностью
учет обоих типов погрешности
z P S X ( t P S X )
2
2
K
zP S X
3
18

19.

Лекция 3. Обработка систематических погрешностей
СПОСОБЫ УСТРАНЕНИЯ ПОСТОЯННЫХ
СИСТЕМАТИЧЕСКИХ ПОГРЕШНОСТЕЙ
Оценка границ неисключенных систематических погрешностей
На основании 10 наблюдений получено следующие значения длины
штрихового метра: 0,9999995 м, 1,0000003 м, 1,0000001 м, 0,9999996 м, 1,0000007 м,
0,9999997 м, 0,9999998 м, 1,0000004 м, 1,0000002 м, 1,0000001 м.
Вычислены неисключенные систематические погрешности:
– из-за неточного определения показателя преломления воздуха: 0,050 мкм;
– из-за неточного значения длин волн 0,046 мкм;
– из-за неточного значения температуры 0,066 мкм;
– из-за неточного определения поправок на размер коллиматорной щели 0,022 мкм.
Требуется определить доверительные границы суммарной погрешности
штрихового метра.
19

20.

Лекция 3. Обработка систематических погрешностей
СПОСОБЫ УСТРАНЕНИЯ ПОСТОЯННЫХ
СИСТЕМАТИЧЕСКИХ ПОГРЕШНОСТЕЙ
Оценка границ неисключенных систематических погрешностей
1 0,050 мкм, 2 0,046 мкм, 3 0,066 мкм, 4 0,022 мкм
– значения неисключенных систематических погрешностей для четырех различных
факторов.
K
N
i2 , 1,4 0,050 0,046 0,066 0,022 0,14 ( мкм)
2
2
2
2
i 1
S X 0,121 мкм, / S X 1,13
K
zP S X
3
2
0,14
2
2,821 0,12 0,49 ( мкм)
1,4
20
2
2
3

21.

Лекция 3. Обработка систематических погрешностей
СПОСОБЫ ОБНАРУЖЕНИЯ ПЕРЕМЕННЫХ
СИСТЕМАТИЧЕСКИХ ПОГРЕШНОСТЕЙ
Графический метод
Метод симметричных
наблюдений
Статистические методы
21

22.

Лекция 3. Обработка систематических погрешностей
СПОСОБЫ ОБНАРУЖЕНИЯ ПЕРЕМЕННЫХ
СИСТЕМАТИЧЕСКИХ ПОГРЕШНОСТЕЙ
Графический метод
X det X 0 Ct
X det X 0 C sin 2 t / T 0
переменная погрешность
22

23.

Лекция 3. Обработка систематических погрешностей
СПОСОБЫ ОБНАРУЖЕНИЯ ПЕРЕМЕННЫХ
СИСТЕМАТИЧЕСКИХ ПОГРЕШНОСТЕЙ
Метод симметричных наблюдений
X X4
X1 X 3
,
, D2 2
2
2
X3 X5
D3
....
2
D1
Если Di D j , то принимается гипотеза о
наличии прогрессирующей погрешности.
С
Линейное изменение систематической
погрешности в методе симметричных наблюдений
X j Xi
t j ti
; X0
X it j X j ti
t j ti
23
.

24.

Лекция 3. Обработка систематических погрешностей
СПОСОБЫ ОБНАРУЖЕНИЯ ПЕРЕМЕННЫХ
СИСТЕМАТИЧЕСКИХ ПОГРЕШНОСТЕЙ
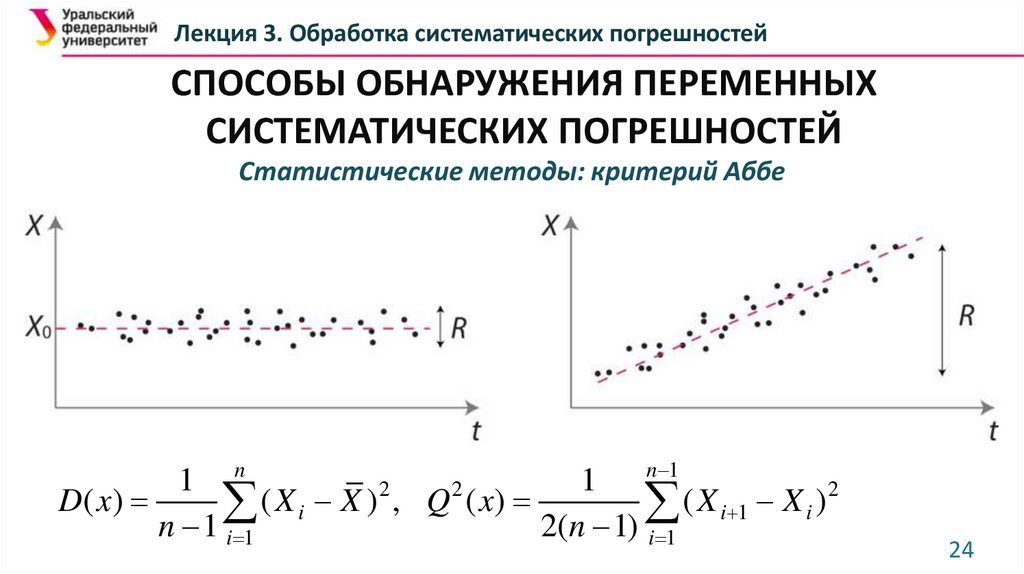
Статистические методы: критерий Аббе
n 1
1 n
1
2
2
2
D( x)
(
X
X
)
,
Q
(
x
)
(
X
X
)
i
i 1 i
n 1 i 1
2(n 1) i 1
24

25.

Лекция 3. Обработка систематических погрешностей
СПОСОБЫ ОБНАРУЖЕНИЯ ПЕРЕМЕННЫХ
СИСТЕМАТИЧЕСКИХ ПОГРЕШНОСТЕЙ
Статистические методы: критерий Аббе
Гипотеза: в анализируемой выборке отсутствует систематический сдвиг.
Алгоритм проверки гипотезы:
1. Рассчитываются дисперсии анализируемых выборок двумя способами:
n 1
1
1 n
2
2
2
Q
(
x
)
(
X
X
)
D( x)
(
X
X
)
,
i 1
i ;
i
2(n 1) i 1
n 1 i 1
2. Рассчитывается значение критерия Аббе:
Q 2[ X ]
q
;
D( x)
3. Проверяется неравенство: q n ,
4. Если неравенство истинно, то гипотеза отклоняется.
25

26.

Лекция 3. Обработка систематических погрешностей
СПОСОБЫ ОБНАРУЖЕНИЯ ПЕРЕМЕННЫХ
СИСТЕМАТИЧЕСКИХ ПОГРЕШНОСТЕЙ
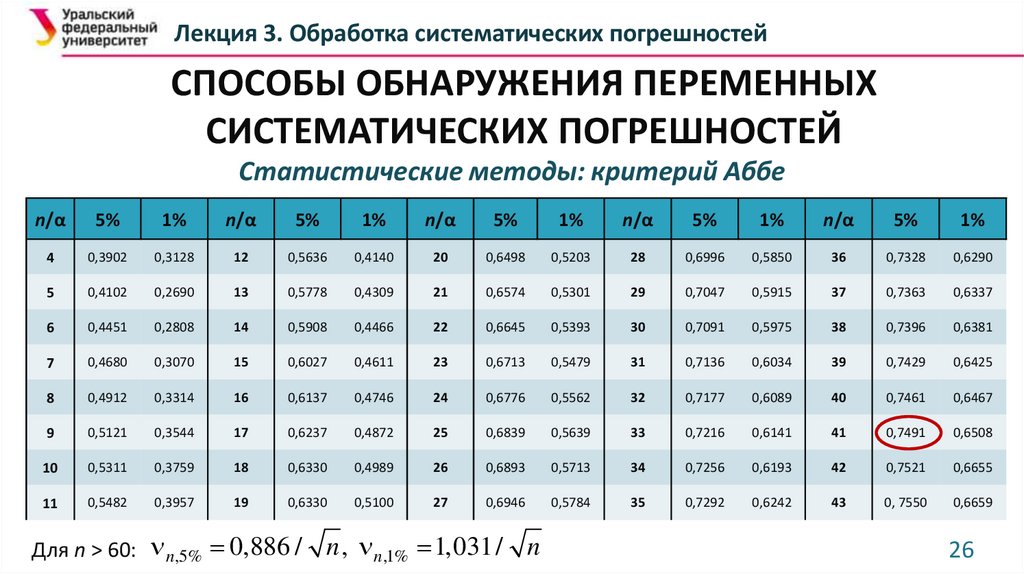
Статистические методы: критерий Аббе
n/α
5%
1%
n/α
5%
1%
n/α
5%
1%
n/α
5%
1%
n/α
5%
1%
4
0,3902
0,3128
12
0,5636
0,4140
20
0,6498
0,5203
28
0,6996
0,5850
36
0,7328
0,6290
5
0,4102
0,2690
13
0,5778
0,4309
21
0,6574
0,5301
29
0,7047
0,5915
37
0,7363
0,6337
6
0,4451
0,2808
14
0,5908
0,4466
22
0,6645
0,5393
30
0,7091
0,5975
38
0,7396
0,6381
7
0,4680
0,3070
15
0,6027
0,4611
23
0,6713
0,5479
31
0,7136
0,6034
39
0,7429
0,6425
8
0,4912
0,3314
16
0,6137
0,4746
24
0,6776
0,5562
32
0,7177
0,6089
40
0,7461
0,6467
9
0,5121
0,3544
17
0,6237
0,4872
25
0,6839
0,5639
33
0,7216
0,6141
41
0,7491
0,6508
10
0,5311
0,3759
18
0,6330
0,4989
26
0,6893
0,5713
34
0,7256
0,6193
42
0,7521
0,6655
11
0,5482
0,3957
19
0,6330
0,5100
27
0,6946
0,5784
35
0,7292
0,6242
43
0, 7550
0,6659
Для n > 60: n ,5% 0,886 /
n , n,1% 1,031 / n
26

27.

Лекция 3. Обработка систематических погрешностей
СПОСОБЫ ОБНАРУЖЕНИЯ ПЕРЕМЕННЫХ
СИСТЕМАТИЧЕСКИХ ПОГРЕШНОСТЕЙ
Статистические методы: критерий Аббе
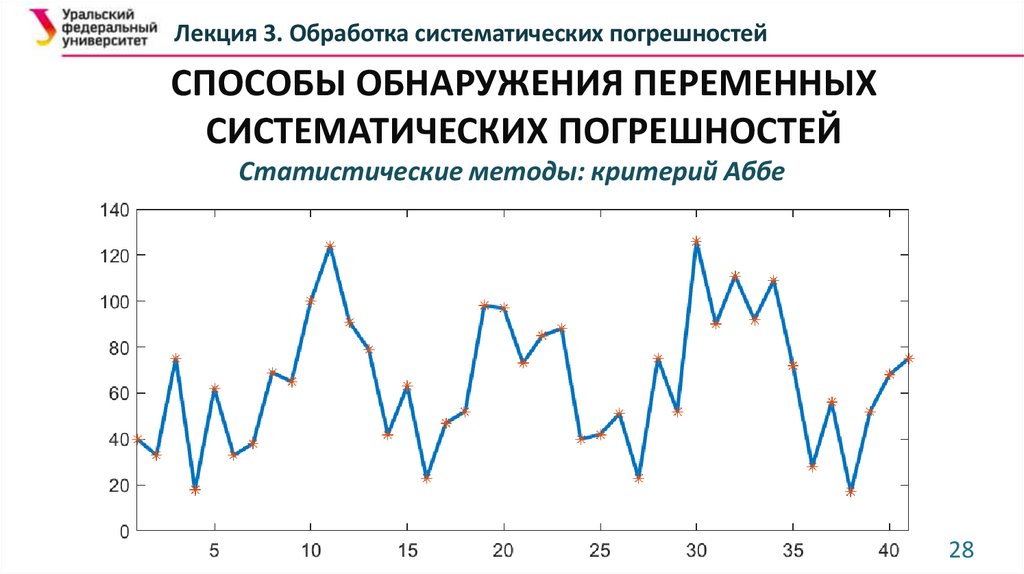
Задача
На цементном заводе в процессе производства ежедневно в
течение 45 дней брались пробы и определялось среднее сопротивление
сжатию контрольных кубов. Результаты наблюдения: 40, 33, 75, 18, 62,
33, 38, 69, 65, 100, 124, 91, 79, 42, 63, 23, 47, 52, 98, 97, 73, 85, 88, 40, 42, 51,
23, 75, 52, 126, 90, 111, 92, 109, 72, 28, 56, 17, 52, 68, 75 (кг/см2).
Определить, присутствует ли систематический сдвиг.
27

28.

Лекция 3. Обработка систематических погрешностей
СПОСОБЫ ОБНАРУЖЕНИЯ ПЕРЕМЕННЫХ
СИСТЕМАТИЧЕСКИХ ПОГРЕШНОСТЕЙ
Статистические методы: критерий Аббе
28

29.

Лекция 3. Обработка систематических погрешностей
СПОСОБЫ ОБНАРУЖЕНИЯ ПЕРЕМЕННЫХ
СИСТЕМАТИЧЕСКИХ ПОГРЕШНОСТЕЙ
Статистические методы: критерий Аббе
1 n
1 n 1
2
2
1. D( x)
( X i X ) 844,98; Q ( x)
( X i 1 X i ) 2 501,76;
n 1 i 1
2(n 1) i 1
Q 2[ X ]
2. q
0,5938;
D( x)
41,5% 0,7491;
3. Проверяем неравенство: q 0,5938 41,5% 0,7491;
4. Неравенство ложно, следовательно, гипотеза отвергается, следовательно, сдвиг
есть на уровне значимости 5%.
29

30.

Лекция 3. Обработка систематических погрешностей
СПОСОБЫ ОБНАРУЖЕНИЯ ПЕРЕМЕННЫХ
СИСТЕМАТИЧЕСКИХ ПОГРЕШНОСТЕЙ
Статистические методы: критерий Фишера
Проводят многократные измерения, состоящие из достаточного числа
серий, каждая из которых соответствует определенным (пусть неизвестным, но
различным) значениям влияющего фактора.
Гипотеза: в анализируемых сериях отсутствует систематический сдвиг.
1. После проведения N измерений их разбивают на s серий по nj результатов
наблюдений (snj = N) в каждой серии и затем устанавливают.
2. Для серий наблюдений рассчитывается внутрисерийная дисперсия:
n
2
ser
n
j
1 s
1 j
2
( X ij X j ) , X j n X ij
N s j 1 i 1
j i 1
30

31.

Лекция 3. Обработка систематических погрешностей
СПОСОБЫ ОБНАРУЖЕНИЯ ПЕРЕМЕННЫХ
СИСТЕМАТИЧЕСКИХ ПОГРЕШНОСТЕЙ
Статистические методы: критерий Фишера
3. Рассчитывается усредненная межсерийная дисперсия:
2
int er
1 s
1 s
2
nj (X j X ) ,X nj X j
N i 1
s 1 j 1
4. Рассчитывается значение критерия Фишера:
2
int
F 2 er
ser
5. Проверяется неравенство: F Fn ,
6. Если неравенство истинно, то гипотеза отклоняется.
31

32.

Лекция 3. Обработка систематических погрешностей
СПОСОБЫ ОБНАРУЖЕНИЯ ПЕРЕМЕННЫХ
СИСТЕМАТИЧЕСКИХ ПОГРЕШНОСТЕЙ
Статистические методы: критерий Фишера
Таблица значений критерия Фишера при уровне значимости q=0,05
s-1
N-s
1
2
3
4
5
6
8
12
24
∞
1
161,45
199,50
215,72
224,57
230,17
233,97
238,89
243,91
249,04
254,32
2
18,51
19,00
19,16
19,25
19,30
19,33
19,37
19,41
19,45
19,50
3
10,13
9,55
9,28
9,12
9,01
8,94
8,84
8,74
8,64
8,53
4
7,71
6,94
6,59
6,39
6,26
6,16
6,04
5,91
5,77
5,63
5
6,61
5,79
5,41
5,19
5,05
4,95
4,82
4,68
5,53
4,36
6
5,99
5,14
4,76
4,53
4,39
4,28
4,15
4,00
3,84
3,67
7
5,59
4,74
4,35
4,12
3,97
3,87
3,73
3,57
3,41
3,23
8
5,32
4,46
4,07
3,84
3,69
5,58
3,44
3,28
3,12
2,93
32

33.

Лекция 3. Обработка систематических погрешностей
СПОСОБЫ ОБНАРУЖЕНИЯ ПЕРЕМЕННЫХ
СИСТЕМАТИЧЕСКИХ ПОГРЕШНОСТЕЙ
Статистические методы: критерий Фишера
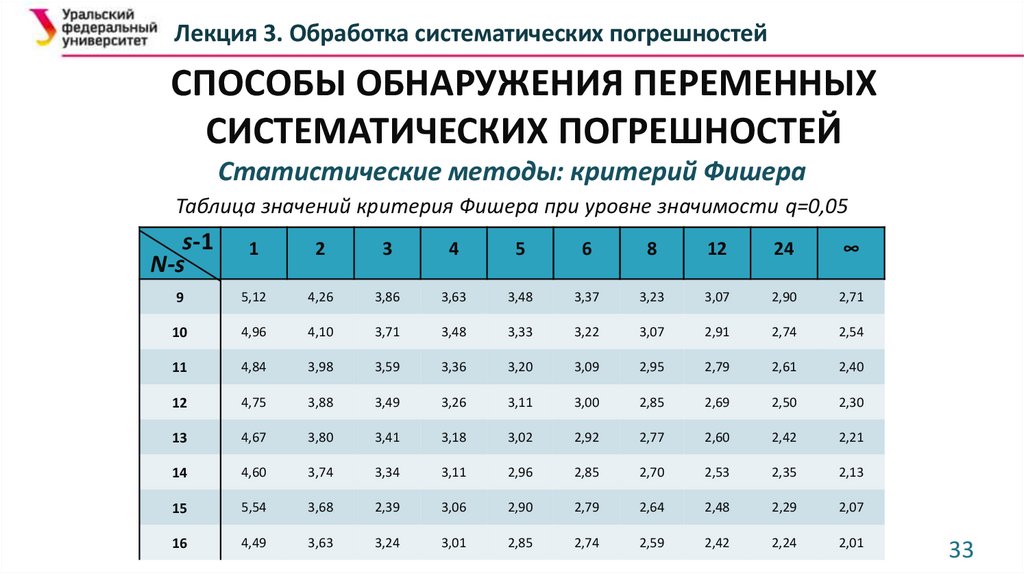
Таблица значений критерия Фишера при уровне значимости q=0,05
s-1
N-s
1
2
3
4
5
6
8
12
24
∞
9
5,12
4,26
3,86
3,63
3,48
3,37
3,23
3,07
2,90
2,71
10
4,96
4,10
3,71
3,48
3,33
3,22
3,07
2,91
2,74
2,54
11
4,84
3,98
3,59
3,36
3,20
3,09
2,95
2,79
2,61
2,40
12
4,75
3,88
3,49
3,26
3,11
3,00
2,85
2,69
2,50
2,30
13
4,67
3,80
3,41
3,18
3,02
2,92
2,77
2,60
2,42
2,21
14
4,60
3,74
3,34
3,11
2,96
2,85
2,70
2,53
2,35
2,13
15
5,54
3,68
2,39
3,06
2,90
2,79
2,64
2,48
2,29
2,07
16
4,49
3,63
3,24
3,01
2,85
2,74
2,59
2,42
2,24
2,01
33

34.

Лекция 3. Обработка систематических погрешностей
СПОСОБЫ ОБНАРУЖЕНИЯ ПЕРЕМЕННЫХ
СИСТЕМАТИЧЕСКИХ ПОГРЕШНОСТЕЙ
Статистические методы: критерий Фишера
Имеется две группы измерений. Результаты измерений первой
группы 2, 3, 1, результаты измерения второй группы: 6, 7, 5.
Определить наличие систематической погрешности.
34

35.

Лекция 3. Обработка систематических погрешностей
СПОСОБЫ ОБНАРУЖЕНИЯ ПЕРЕМЕННЫХ
СИСТЕМАТИЧЕСКИХ ПОГРЕШНОСТЕЙ
Статистические методы: критерий Фишера
N 6 – объем наблюдений;
s 2 – количество серий;
n1 3, n2 3 – объемы серий.
2. Внутрисерийная дисперсия:
n
1 j
1
1 n2
1
X1
X
1
2
3
2,
X
X
5 6 7 6,
ij
2
ij
n j i 1
3
n 2 i 1
3
n
j
1 s
1
2
2
ser
( X ij X j )
2 2 1.
N s j 1 i 1
6 2
35

36.

Лекция 3. Обработка систематических погрешностей
СПОСОБЫ ОБНАРУЖЕНИЯ ПЕРЕМЕННЫХ
СИСТЕМАТИЧЕСКИХ ПОГРЕШНОСТЕЙ
Статистические методы: критерий Фишера
3. Межсерийная дисперсия:
1 s
1
X n j X j 3 2 3 6 4,
N i 1
6
3 4 4
1 s
2
2
int er
nj(X j X )
24;
s 1 j 1
1
2
int
er
4. Рассчитываем значение критерия Фишера: F
24;
2
ser
5. Проверяем неравенство: F 24 FN ,s , 7,71;
6. Неравенство истинно, гипотеза отклоняется, есть сдвиг на уровне значимости 5%. 36

37.

Лекция 3. Обработка систематических погрешностей
СПОСОБЫ ОБНАРУЖЕНИЯ ПЕРЕМЕННЫХ
СИСТЕМАТИЧЕСКИХ ПОГРЕШНОСТЕЙ
Статистические методы: критерий Вилкоксона
Выполняется серия измерений для двух связанных выборок:
{ X 1, X 2 ... X n } и {Y1, Y2 ...Ym },причем n m 5;
Гипотеза: в анализируемой выборке присутствует систематический сдвиг.
1. Рассчитаются значения разностей пар двух выборок;
2. Выделяются нетипичные сдвиги;
3. Модулям разностей присваиваются связанные ранги;
4. Рассчитывается сумма рангов R, соответствующих нетипичным сдвигам;
n
5. Проверяется неравенство:
R j Tcrit ;
j 1
6. Если неравенство истинно, то гипотеза отклоняется.
37

38.

Лекция 3. Обработка систематических погрешностей
СПОСОБЫ ОБНАРУЖЕНИЯ ПЕРЕМЕННЫХ
СИСТЕМАТИЧЕСКИХ ПОГРЕШНОСТЕЙ
Статистические методы: критерий Вилкоксона
38

39.

Лекция 3. Обработка систематических погрешностей
СПОСОБЫ ОБНАРУЖЕНИЯ ПЕРЕМЕННЫХ
СИСТЕМАТИЧЕСКИХ ПОГРЕШНОСТЕЙ
Статистические методы: критерий Вилкоксона
Сравнить между собой две выборки с помощью критерия Вилкоксона.
39

40.

Лекция 3. Обработка систематических погрешностей
СПОСОБЫ ОБНАРУЖЕНИЯ ПЕРЕМЕННЫХ
СИСТЕМАТИЧЕСКИХ ПОГРЕШНОСТЕЙ
Статистические методы: критерий Вилкоксона
1. Рассчитываем значения разностей пар двух выборок:
40

41.

Лекция 3. Обработка систематических погрешностей
СПОСОБЫ ОБНАРУЖЕНИЯ ПЕРЕМЕННЫХ
СИСТЕМАТИЧЕСКИХ ПОГРЕШНОСТЕЙ
Статистические методы: критерий Вилкоксона
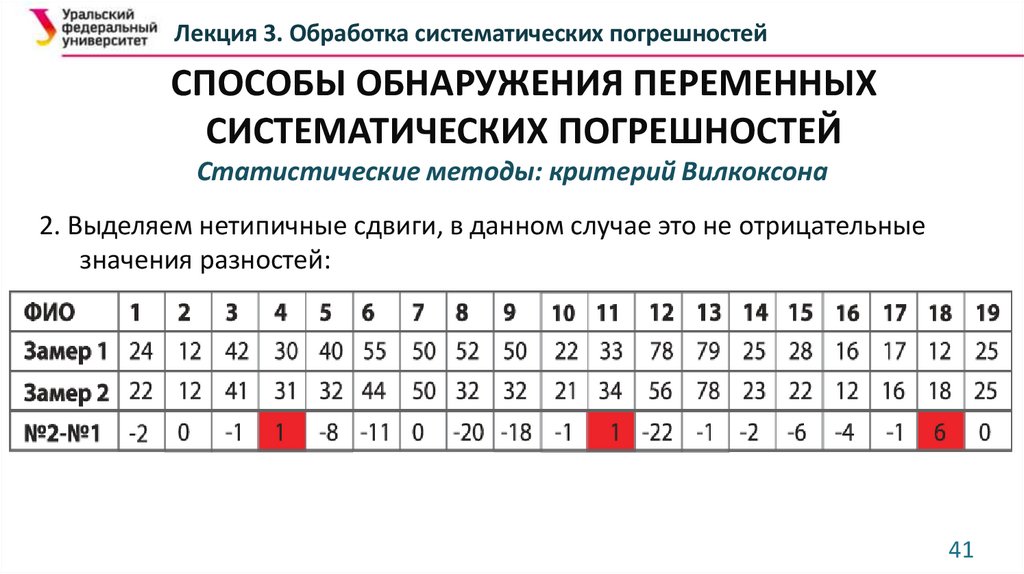
2. Выделяем нетипичные сдвиги, в данном случае это не отрицательные
значения разностей:
41

42.

Лекция 3. Обработка систематических погрешностей
СПОСОБЫ ОБНАРУЖЕНИЯ ПЕРЕМЕННЫХ
СИСТЕМАТИЧЕСКИХ ПОГРЕШНОСТЕЙ
Статистические методы: критерий Вилкоксона
3. Присваиваем модулям разностей связанные ранги :
42

43.

Лекция 3. Обработка систематических погрешностей
СПОСОБЫ ОБНАРУЖЕНИЯ ПЕРЕМЕННЫХ
СИСТЕМАТИЧЕСКИХ ПОГРЕШНОСТЕЙ
Статистические методы: критерий Вилкоксона
4. Рассчитываем сумму рангов R, соответствующих нетипичным сдвигам :
R 6,5 6,5 13,5 26,6
43

44.

Лекция 3. Обработка систематических погрешностей
СПОСОБЫ ОБНАРУЖЕНИЯ ПЕРЕМЕННЫХ
СИСТЕМАТИЧЕСКИХ ПОГРЕШНОСТЕЙ
Статистические методы: критерий Вилкоксона
5. Проверяем неравенство:
n
R j 26,5 T19,1% 37;
j 1
n
R j 26,5 T19,5% 53;
j 1
6. Неравенство ложно, гипотеза отклоняется, систематический сдвиг отсутствует на
уровне значимости 1%.
44

45.

Лекция 3. Обработка систематических погрешностей
ОБРАБОТКА РЕЗУЛЬТАТОВ
ПРЯМЫХ МНОГОКРАТНЫХ ИЗМЕРЕНИЙ
1. Определение закона распределения случайных погрешностей измерений
Построение гистограммы
по результатам наблюдений
Построение полигона
по результатам наблюдений
Построение кумулятивной
кривой по результатам
наблюдений
45

46.

Лекция 3. Обработка систематических погрешностей
ОБРАБОТКА РЕЗУЛЬТАТОВ
ПРЯМЫХ МНОГОКРАТНЫХ ИЗМЕРЕНИЙ
1. Определение закона распределения случайных погрешностей измерений
Критерий Пирсона χ2
(хи-квадрат), критерий
Мизеса-Смирнова (ω2)
Составной критерий
(d-критерий)
Решение принимается
на основании анализа
априорной информации
При объеме выборки
более 50 элементов
При объеме выборки
от 15 до 50 элементов
При объеме выборки
менее 15 элементов
46

47.

Лекция 3. Обработка систематических погрешностей
ОБРАБОТКА РЕЗУЛЬТАТОВ
ПРЯМЫХ МНОГОКРАТНЫХ ИЗМЕРЕНИЙ
1. Определение закона распределения случайных погрешностей измерений
Критерий согласия Пирсона χ2 (хи-квадрат)
1. Разброс разбивается на интервалы равной длины. Число интервалов r определяется
объемом выборки N:
N
r
N
r
40–100
7–9
500–1000
10–16
100–500
8–12
1000–10000
12–22
2. Рассчитываются относительные частоты nj для каждого из интервалов. Интервалы,
содержащие менее 5 наблюдений, объединяют с соседними. Однако, если число
таких интервалов составляет менее 20% от их общего количества, допускаются
интервалы с частотой более 2.
47

48.

Лекция 3. Обработка систематических погрешностей
ОБРАБОТКА РЕЗУЛЬТАТОВ
ПРЯМЫХ МНОГОКРАТНЫХ ИЗМЕРЕНИЙ
1. Определение закона распределения случайных погрешностей измерений
Критерий согласия Пирсона χ2 (хи-квадрат)
3. Рассчитывается величина хи-квадрат:
2
e
j 1
(n j Np j ) 2
Np j
,
где pj — вероятность попадания изучаемой случайной величины в j-ый интервал,
вычисляемая в соответствии с гипотетическим законом распределением f(x).
4. Проверяется неравенство:
2
2 , f ;
5. Если неравенство истинно, то гипотеза о принадлежности выборки гипотетическому
закону распределения f(x) принимается.
48

49.

Лекция 3. Обработка систематических погрешностей
ОБРАБОТКА РЕЗУЛЬТАТОВ
ПРЯМЫХ МНОГОКРАТНЫХ ИЗМЕРЕНИЙ
1. Определение закона распределения случайных погрешностей измерений
Критерий согласия Пирсона χ2 (хи-квадрат)
f/α
10%
5%
1%
f/α
10%
5%
1%
f/α
10%
5%
1%
f/α
10%
5%
1%
1
2,71
3,84
6,63
9
14,68
16,92
21,67
17
24,77
27,59
33,41
25
34,38
37,65
44,31
2
4,61
5,99
9,21
10
15,99
18,31
23,21
18
25,99
28,87
34,81
26
35,38
38,89
45,64
3
6,25
7,81
11,34
11
17,28
19,68
24,72
19
27,20
30,14
36,19
27
36,74
40,11
46,96
4
7,78
9,49
13,28
12
18,55
21,03
26,22
20
28,41
31,41
37,57
28
37,92
41,34
48,28
5
9,24
11,07
15,09
13
19,81
22,36
27,69
21
29,62
32,67
38,93
29
39,09
42,56
49,59
6
10,64
12,59
16,81
14
21,06
23,68
29,14
22
30,81
33,92
40,29
30
40,26
43,77
50,89
7
12,02
14,07
18,48
15
22,31
25,00
30,58
23
32,01
35,17
41,64
40
51,80
55,76
63,69
8
13,36
15,51
20,09
16
23,54
26,30
32,00
24
33,20
36,42
42,98
50
63,17
67,50
76,15
49

50.

Лекция 3. Обработка систематических погрешностей
ОБРАБОТКА РЕЗУЛЬТАТОВ
ПРЯМЫХ МНОГОКРАТНЫХ ИЗМЕРЕНИЙ
1. Определение закона распределения случайных погрешностей измерений
Критерий Мизеса-Смирнова (ω2)
1. Ранжируются результаты наблюдений Xi;
2
2i 1
1
2. Рассчитывается величина омега-квадрат: 2 F ( X i )
;
2 N 12 N
i 1
N
где F(Xi) — значения предполагаемой теоретической функции распределения,
W
2i 1
— накопленная частость;
2n
4. Проверяется неравенство: , f ;
2
2
5. Если неравенство истинно, то гипотеза о принадлежности выборки гипотетическому
закону распределения F(x) принимается.
50

51.

Лекция 3. Обработка систематических погрешностей
ОБРАБОТКА РЕЗУЛЬТАТОВ
ПРЯМЫХ МНОГОКРАТНЫХ ИЗМЕРЕНИЙ
1. Определение закона распределения случайных погрешностей измерений
Составной критерий (d-критерий)
1. Находят отношение:
N
d
Xi X
1
i 1
N
S
*
,
1 n
2
где S
(
X
X
)
— смещенная оценка среднего квадратического отклонения;
i
n i 1
*
2. Проверяется условие: d min d d max ;
51

52.

Лекция 3. Обработка систематических погрешностей
ОБРАБОТКА РЕЗУЛЬТАТОВ
ПРЯМЫХ МНОГОКРАТНЫХ ИЗМЕРЕНИЙ
1. Определение закона распределения случайных погрешностей измерений
Составной критерий (d-критерий)
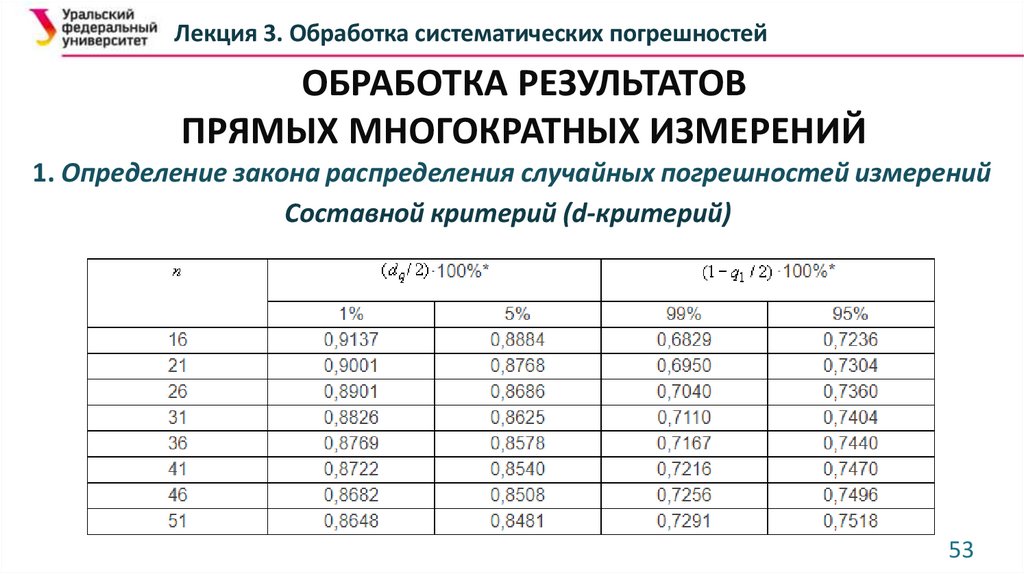
3. При выполнении условия проверяются условия для всех Xi:
X i X zP S X ;
4. Если неравенства истины для (n – m) разностей, то гипотеза о принадлежности
выборки к нормальному распределению принимается.
При 10<n<20 m=1;
При 21<n<49 m=2;
52

53.

Лекция 3. Обработка систематических погрешностей
ОБРАБОТКА РЕЗУЛЬТАТОВ
ПРЯМЫХ МНОГОКРАТНЫХ ИЗМЕРЕНИЙ
1. Определение закона распределения случайных погрешностей измерений
Составной критерий (d-критерий)
53

54.

Лекция 3. Обработка систематических погрешностей
ОБРАБОТКА РЕЗУЛЬТАТОВ
ПРЯМЫХ МНОГОКРАТНЫХ ИЗМЕРЕНИЙ
2. Определение точечных оценок закона
распределения результатов измерений
— Исключение промахов в соответствии с рассмотренными критериями;
— Расчет среднего арифметического значения, оценка СКО результата измерения,
оценка СКО среднего арифметического значения по формулам:
1 n
X Xi , SX
N i 1
1 n
2
(
X
X
)
, SX
i
N 1 i 1
n
1
2
(
X
X
)
;
i
N ( N 1) i 1
54

55.

Лекция 3. Обработка систематических погрешностей
ОБРАБОТКА РЕЗУЛЬТАТОВ
ПРЯМЫХ МНОГОКРАТНЫХ ИЗМЕРЕНИЙ
3. Определение доверительных интервалов случайной погрешности
— При числе наблюдений n ⩾ 10–15 и нормальном распределении границы
доверительных интервалов определяют с помощью Z-распределения при
заданном уровне доверительной вероятности;
zP S X ;
— При числе наблюдений n < 10–15 и нормальном распределении границы
доверительных интервалов определяют с помощью t-распределения при
заданном уровне доверительной вероятности;
t P S X .
55

56.

Лекция 3. Обработка систематических погрешностей
ОБРАБОТКА РЕЗУЛЬТАТОВ
ПРЯМЫХ МНОГОКРАТНЫХ ИЗМЕРЕНИЙ
4. Определение границ неисключенной систематической погрешности Θ
N
i , N 3
i 1
– границы неисключенной систематической погрешности.
N
K
2
i , N 3
i 1
/ S X 0,8
/ SX 8
0,8 / S X 8
пренебрегают неисключенной
систематической погрешностью
пренебрегают случайной
погрешностью
учет обоих типов погрешности
56

57.

Лекция 3. Обработка систематических погрешностей
ОБРАБОТКА РЕЗУЛЬТАТОВ
ПРЯМЫХ МНОГОКРАТНЫХ ИЗМЕРЕНИЙ
5. Запись результата измерения
Результат измерения записывается в виде
X , P PД
При отсутствии данных о виде функций распределений составляющих
погрешности оценки измеряемой величины и необходимости дальнейшей обработки
результатов измерений или анализа погрешностей оценки измеряемой величины
представляют в форме
X ; S X ; n;
57