Similar presentations:
Модели оптимального планирования
1.
Моделиоптимального
планирования
§20 (учебник)
2.
Объекты планирования –разные системы:
• Деятельность отдельного предприятия.
• Отрасли промышленности или с/х региона,
государства.
2
3.
Постановка задачи планированиявыглядит следующим образом:
• имеются некоторые плановые показатели: X, Y,
и др.;
• имеются некоторые ресурсы: R1, R2 и др., за
счет которых эти плановые показатели могут
быть достигнуты. Эти ресурсы практически
всегда ограничены;
• имеется определенная стратегическая цель,
зависящая от значений X, Y и др. плановых
показателей, на которую следует ориентировать
планирование.
4.
Оптимальный план:Нужно определить значение плановых
показателей с учетом ограниченности ресурсов
при условии достижения стратегической цели.
5.
Пример объекта оптимальногопланирования
Детский сад
Плановые показатели
1. Количество детей
2. Количество
воспитателей
Основные ресурсы
деятельности
1. Объем
финансирования
2. Площадь
помещения
Стратегические цели: сохранение и укрепление здоровья детей.
Количественная мера целей: минимизация заболеваемости
воспитанников детского сада.
5
6.
Для решения задачи на компьютере нужнопостроить математическую модель.
Следовательно, всё, о чем говорилось в примерах,
должно быть переведено на язык чисел, формул,
уравнений и других средств математики. В полном
объеме для реальных систем эта задача очень
сложная.
Рассмотрим очень простой пример, из которого вы
получите представление об одном из подходов к
решению задачи оптимального планирования.
7.
«Школьный кондитерский цех».Количество изделий – 700 штук/ день.
Пирожные – не более 250 штук / день (если не выпекать
пирожки)
Пирожки – около 1000 штук / день (если не выпекать пирожные)
Рабочий день – 8 часов.
Стоимость пирожного в 2 раза выше стоимости пирожка.
ЗАДАЧА: составить такой дневной план производства, чтобы
обеспечить наибольшую выручку кондитерского цеха.
7
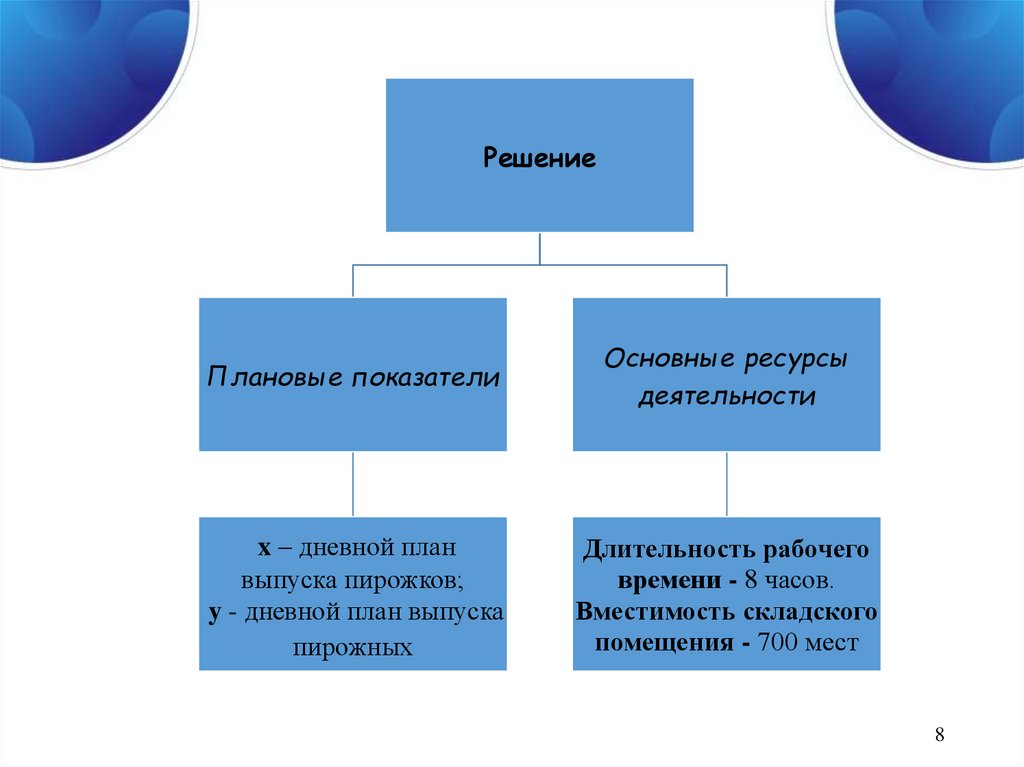
8.
РешениеПлановые показатели
Основные ресурсы
деятельности
x – дневной план
выпуска пирожков;
y - дневной план выпуска
пирожных
Длительность рабочего
времени - 8 часов.
Вместимость складского
помещения - 700 мест
8
9.
Время изготовления пирожка – t мин.Время изготовления пирожного - 4t мин, т.к. если целый день готовить
лишь пирожки, то получим 1000 шт, если только пирожные, то 250 шт,
следовательно, время производства пирожного в 4 раза выше пирожка.
tх + 4ty = t (х + 4y)
суммарное время на изготовление х пирожков и y пирожных.
9
10.
ОграниченияНо суммарное время не может быть больше длительности рабочего дня.
t (х + 4y) <= 8 *60 (для удобства выразим в минутах)
t (х + 4y) <= 480
На изготовление одного пирожка тратится – 480/1000 = 0,48 мин.
Время изготовления пирожка – t мин
0,48*(х + 4y) <= 480
1) х + 4y <= 1000
2) х + y <= 700 - общее число изделий
10
11.
Решение системы неравенств:х + 4y <= 1000;
х + y <= 700;
х >= 0; (не можем же мы произвести -1 пирожок)
y >= 0; (и -1 пирожное тоже)
11
12.
Стратегическая цель:получение максимальной выручки.
Выручка – это стоимость всей проданной продукции.
Пусть цена одного пирожка – r рублей (r - константа)
Цена одного пирожного – 2r рублей (следует из условия).
rх + 2ry = r (х + 2y)
– стоимость всей продукции.
F (x, y) = r (х + 2y)
ЦЕЛЕВАЯ ФУНКЦИЯ
12
13.
Математическая задача:Требуется найти значение плановых показателей x
и y, удовлетворяющих данной системе неравенств
и придающих максимальное значение целевой
функции.
Математическое программирование
(линейное).
13
14.
• Система написанных выше неравенствпредставляется на координатной плоскости
четырехугольником, ограниченным четырьмя
прямыми, соответствующими линейным
уравнениям:
• х + 4у = 1000,
• х + у = 700,
• х = 0 (ось У).
• у = 0 (ось X)
15.
ПРАКТИКА• Цель понятна, разберемся со средствами. В Excel
существует «Поиск решения» в разделе
«Данные», который поможет нам определить
плановые показатели.
• Если такой кнопки нет, можно добавить
• Файл – Параметры – Надстройки – Перейти… Поиск решения (поставить галочку).














 informatics
informatics








