Модели оптимального планирования

1.

Тема: модели оптимального
планирования
Работу выполнили:
Тепляков Даниила Александрович
Зорин Иван Денисович
Ханнанов Айгиз

2.

Сущность задач оптимального
планирования
Оптимальное планирование – комплекс методов который
позволяет выбрать из многих возможных планов или
программы наилучший с точки зрения заданного критерия
оптимальности при определённых ограничениях.
В экономическом анализе критерий оптимальности –
показатель
показывающий
предельную
меру
экономического
эффекта
принимаемого
решением
(максимум прибыли, минимум трудозатрат, наименьшее
время достижения цели и т.д.).

3.

Объекты планирования
• деятельность отдельного предприятия,
• деятельность отрасли промышленности или
•сельского хозяйства,
• деятельность региона,

4.

Стратегическая цель
Решение задачи оптимального
планирования сводится к
построению целевой функции и
назначению определенных условий
для ее величины: чаще всего
максимума или минимума.

5.

Сущность задач оптимального
планирования
Основные задачи:
1. Правильно и чётко формулировать цели
экономической системы в целом и каждого
его звена.
2.
Отбирать критерий оптимальности для всего
комплекса задач планирования.
3. Решать каждую задачу планирования в
отдельности
оптимально
(находить
единственно наилучшее решение с учётом
избранных критериев оптимальности).

6.

Классификация задач
оптимального планирования
I.
По
характеру
переменными:
1. линейные;
2. нелинейные.
взаимосвязи
между
II. По характеру изменения переменных:
1. непрерывный;
2. дискретный.
III. По характеру учёта факторов времени:
1. статические;
2. динамические.
Оптимальное планирование основано на
решении
задач
математического
программирования.

7.

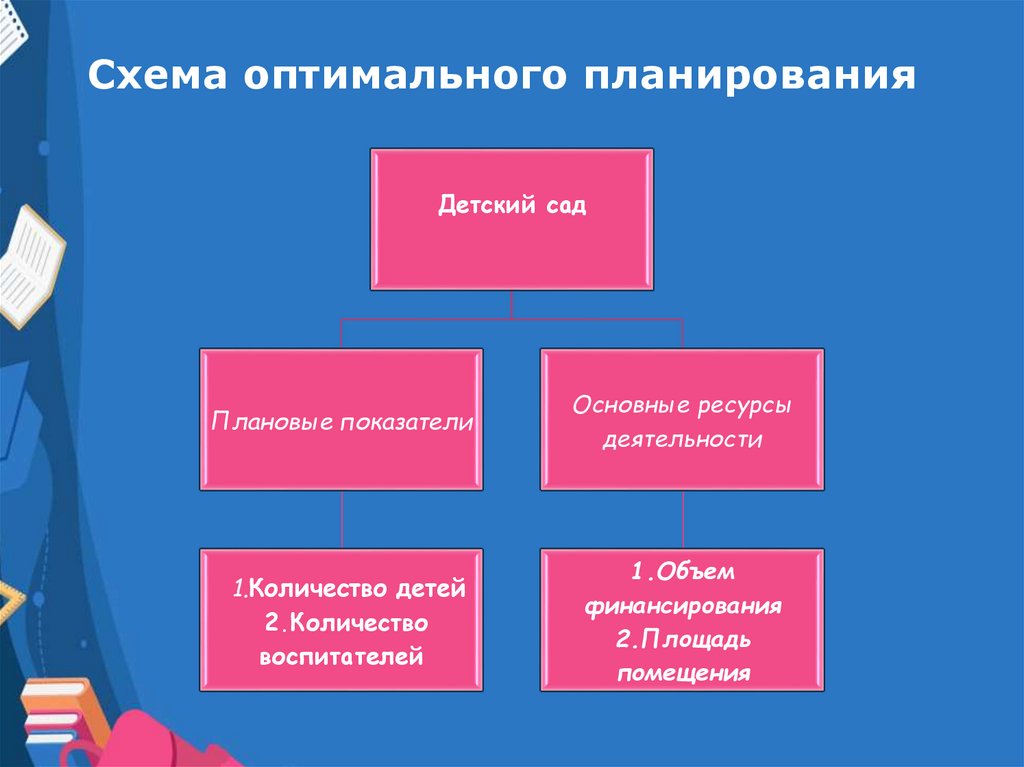
Схема оптимального планирования
Детский сад
Плановые показатели
Основные ресурсы
деятельности
1.Количество детей
2.Количество
воспитателей
1.Объем
финансирования
2.Площадь
помещения

8.

Процесс постановки и решения
задач по оптимальному
планированию
1.Осмысление задачи, выделение наиболее важных
качеств и т.д
2.Введение неизвестных
3.Создание целевой функции
4.Составление системы ограничений
5.Решение задач на пк

9.

ЦЕЛЕВАЯ ФУНКЦИЯ
А теперь перейдем к формализации стратегической цели: получению
максимальной выручки. Выручка — это стоимость всей проданной
продукции. Пусть цена одного пирожка — r рублей. По условию задачи,
цена пирожного в два раза больше, т. е. 2r рублей. Отсюда стоимость всей
произведенной за день продукции равна
rх + 2rу = r(х + 2у).
Целью производства является получение максимальной выручки. Будем
рассматривать записанное выражение как функцию от х, у:
F(x, у) = r(х + 2у).
Она называется целевой функцией.
Поскольку значение r — константа, максимальное значение F(x, у) будет
достигнуто при максимальной величине выражения (х + 2у). Поэтому в
качестве целевой функции можно принять f(x, у) = х +
2у.
Следовательно, получение оптимального плана свелось к следующей
математической задаче:
Требуется найти значения плановых показателей х и у, удовлетворяющих
данной системе неравенств и придающих максимальное значение целевой
функции.

10.

ПРИМЕР ЗАДАЧИ
Школьный кондитерский цех готовит пирожки и пирожные. В
силу ограниченности
- За день можно приготовить не более 700 штук изделий.
- Рабочий день в кондитерском цехе длится 8 часов.
- Производство пирожных более трудоемко, поэтому если
выпускать только их, за день можно произвести не более 250
штук, пирожков же можно произвести 1000 штук (если при
этом не выпускать пирожных).
- Стоимость пирожного вдвое выше, чем стоимость пирожка.
Требуется составить такой дневной план производства,
чтобы обеспечить наибольшую выручку кондитерского
цеха.