Similar presentations:
Теодолитная съемка. Обработка результатов теодолитной съемки. Построение плана
1.
ТЕОДОЛИТНАЯ СЪЕМКА. ОБРАБОТКА РЕЗУЛЬТАТОВТЕОДОЛИТНОЙ СЪЕМКИ. ПОСТРОЕНИЕ ПЛАНА
Получение контурного плана местности с помощью теодолита и мерной
ленты (или дальномера) называется теодолитной съемкой.
При теодолитной съемке рельеф не изображается.
Съемка ведется по принципу от общего к частному, т. е. на местности
выбираются и закрепляются опорные точки, определяются их
координаты, а с них ведется съемка подробностей.
Совокупность таких точек называется съемочной сетью, которая
строится в виде теодолитных ходов, представляющих с собой систему
ломаных линий, в которых углы измеряются теодолитом, а стороны
мерной лентой или дальномером.
2.
Обработка результатов теодолитной съемки3.
4.
5.
в) Теодолитные ходы прокладываются с учетом надежного контроля.Поэтому в районах, где отсутствуют точки геодезической сети или они
располагаются близко друг от друга, рекомендуется прокладывать
замкнутые полигоны, внутри которых прокладываются диагональные ходы,
образующие узловые точки. Диагональные ходы позволяют сгущать систему
съемочных точек и осуществлять дополнительный контроль измерений.
Схема проложения замкнутого теодолитного хода.
С
м
αM-l
dl-ll
l
β2
β1
Диагональный теодолитный ход
dV-l
Опорный пункт
геодезической сети.
β3
β5
V
ll
lll
β4
dlV-V
lV
Зная координаты точки М, значения дирекционного угла αM-l , а также внутренние углы β и горизонтальные
проложения сторон d, можно рассчитать координаты всех вершин полигона.
6.
Камеральные работы при оформлении результатов теодолитной съемкиРис. 97. Схема замкнутого теодолитного хода
7.
ОБРАБОТКА РЕЗУЛЬТАТОВ ИЗМЕРЕНИЙВ процессе камеральной обработки устанавливается соответствие
результатов измерений, требованиям точности съемки. Камеральная
обработка включает в себя:
1. Проверка записей и вычислений в полевых журналах.
2. Вычисление горизонтальных проложений линий.
3. Вычисляются координаты точек теодолитного хода.
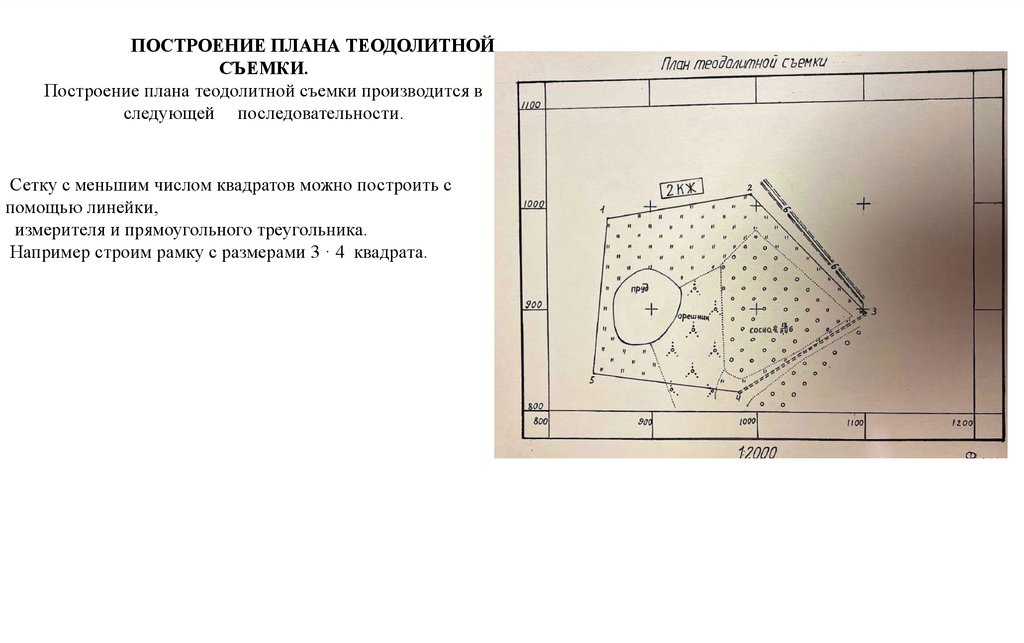
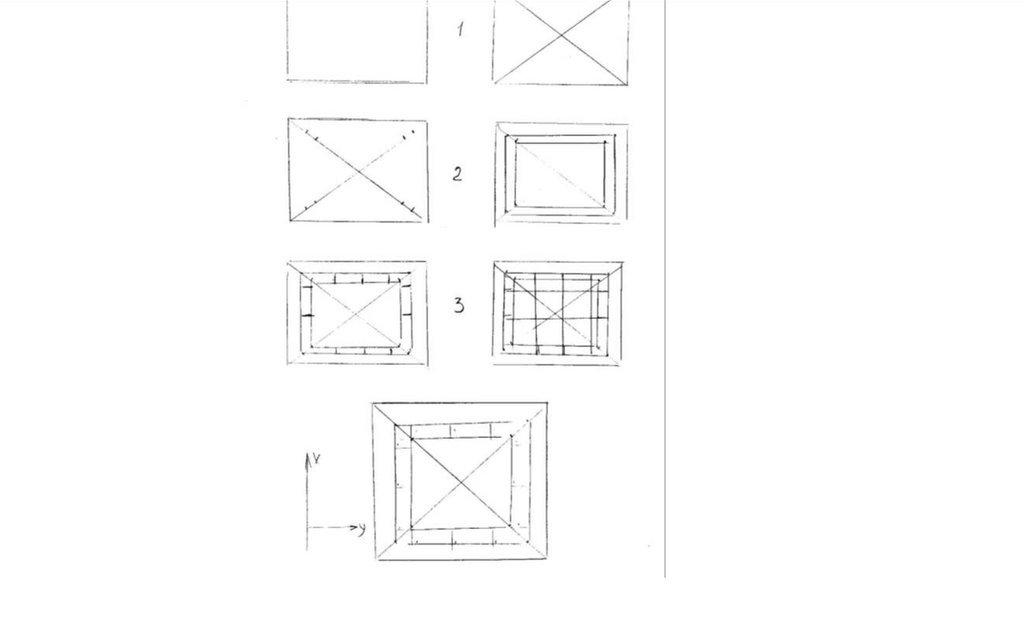
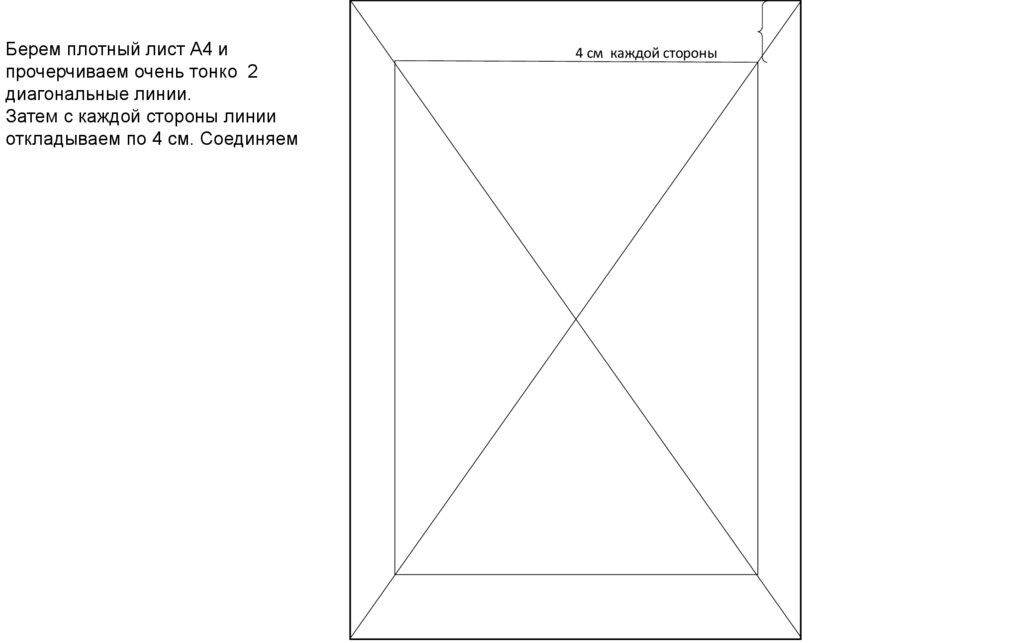
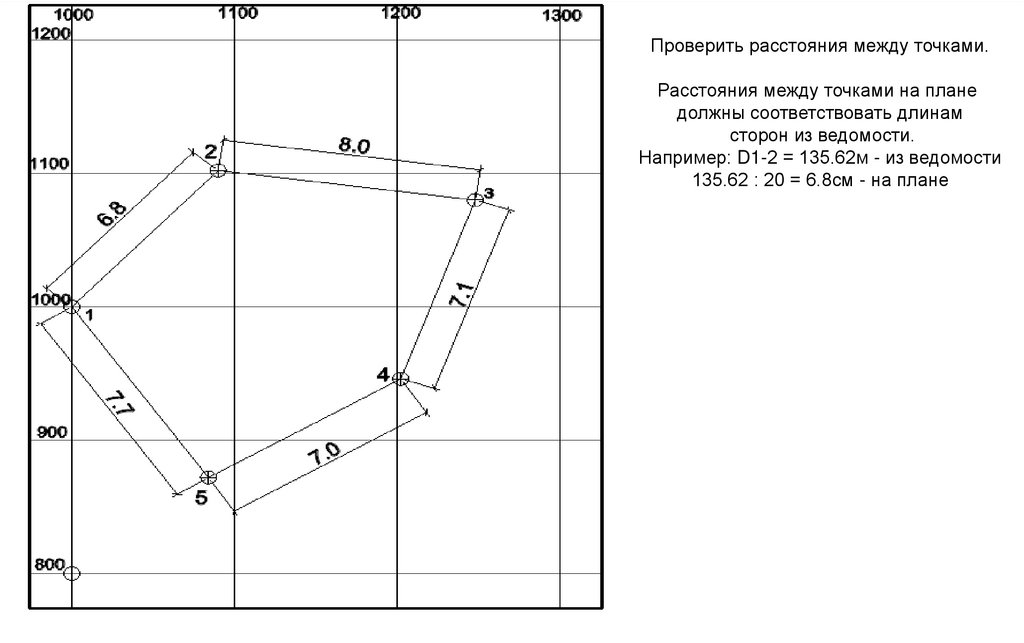
4. Построение плана теодолитной съемки.
8.
ОБРАБОТКА РЕЗУЛЬТАТОВ ИЗМЕРЕНИЙ ПРИ ТЕОДОЛИТНОЙСЪЕМКЕ.
Камеральная обработка результатов съемки заключается в выполнении
вычислительных и графических работ, целью которых является определение
координат точек теодолитного хода и построение плана местности в
заданном масштабе.
Для решения прямой геодезической задачи, для вычисления координаты
точки, необходимо знать координаты предыдущей по ходу точки Х1,У1,
горизонтальное проложение d 1-2 и дирекционный угол α1-2 линии,
соединяющей эти точки.
Координаты вычисляются по формулам.
Х2=Х1 + d1-2 · cos α1-2.
У2=У1 + d1-2 · sin α1-2.
Значения горизонтальных углов и величины длин сторон теодолитных ходов,
записанные в полевые журналы несут в себе ошибки, поэтому суммы
измеренных углов теодолитного хода отличаются от теоретических сумм
этих углов, а суммы приращения координат от теоретических сумм этих
приращений. Разность между практическими и теоретическими суммами
называются невязками и обозначаются буквой f.
9.
10.
Порядок определения исходных данных для выполнения заданияпо обработке материалов теодолитного хода
I . Координаты X1 Y1 сокращенные установлены следующие:
- десятки и единицы километров для всех студентов одинаковые
X=78, Y=48; (см.МУ)
- сотнями, десятками и единицами метров будут последние три цифры студенческого билета;
- десятые и сотые значения в координатах – последние три и две цифры студенческого билета соответственно.
Примеры:
У студента 1 последние три цифры студенческого билета 250, начальные координаты
принимаются X1=78250,50 Y1=48250,50
У студента группы 2 последние три цифры студенческого билета 368, начальные координаты принимаются
X1=78368,68 Y1=48368,68
II.Исходный дирекционный угол α1-2 устанавливается следующим образом:
- градусы – последние 3 цифры студенческого билета. Если число равно 360 или большему, то из его величины
вычитается 360;
- минуты – последние 2 цифры номера студенческого билета. Если число 60 или больше, то из его величины
вычитается 60;
Примеры:
У студента последние три цифры студенческого билета 250. Исходный дирекционный угол принимается равным
α1-2=250°50'
У студента группы последние три цифры студенческого билета 368 Исходный дирекционный угол
принимается равным α1-2= 8°08'
11.
Исправленные углыДирекционные углы
3
4
5
1
105º24´
6
7
Приращения
вычисленные
Поправки к
приращениям
Приращения
исправленные
Координаты
Длина линии d
Поправки к углам
2
Величина
Измеренные углы
1
Румбы
Название
Номер углов
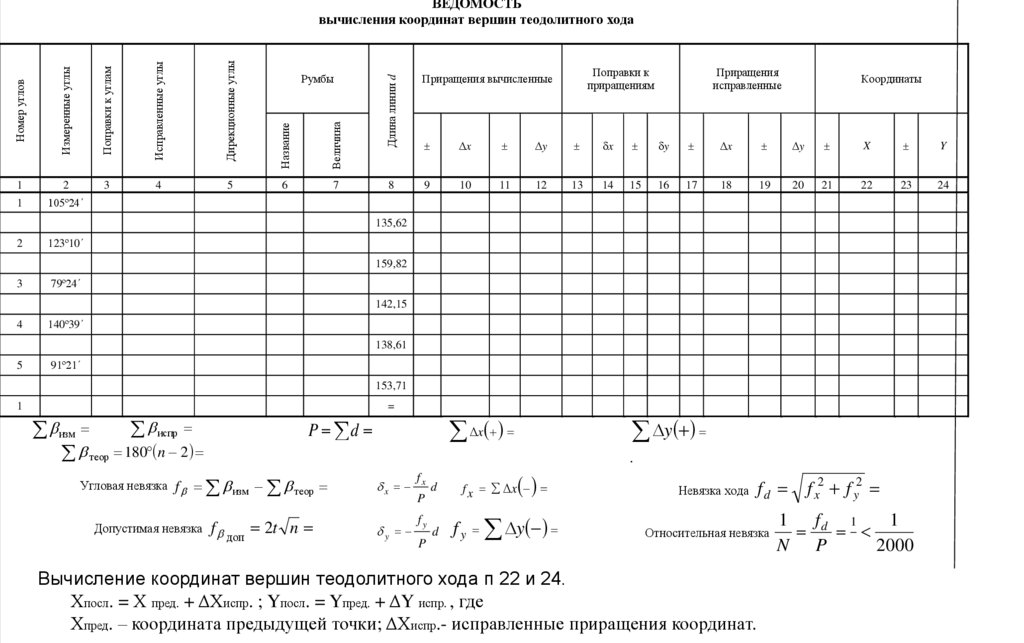
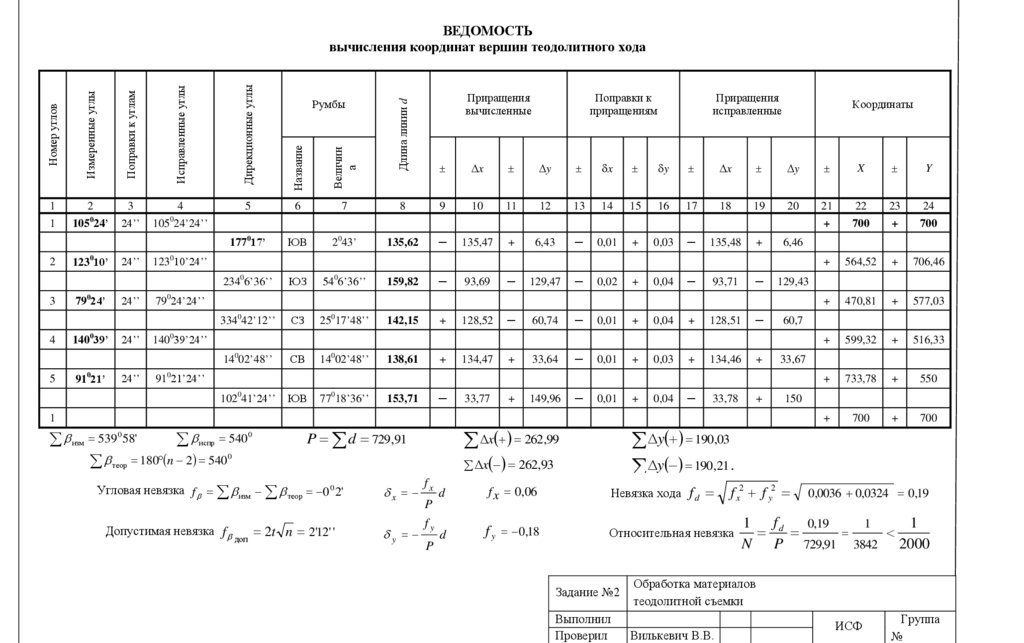
ВЕДОМОСТЬ
вычисления координат вершин теодолитного хода
x
y
x
y
x
y
X
Y
8
9
10
11
12
13
14
15
16
17
18
1
9
20
21
22
23
24
135,62
2
123º10´
159,82
3
79º24´
142,15
4
140º39´
138,61
5
91º21´
153,71
1
испр
изм
теор 180 n 2
Угловая невязка f
x
изм теор
x
2t n
доп
y
Допустимая невязка f
y
y .
x
P d
fx
d
fx
d
fy
P
fy
P
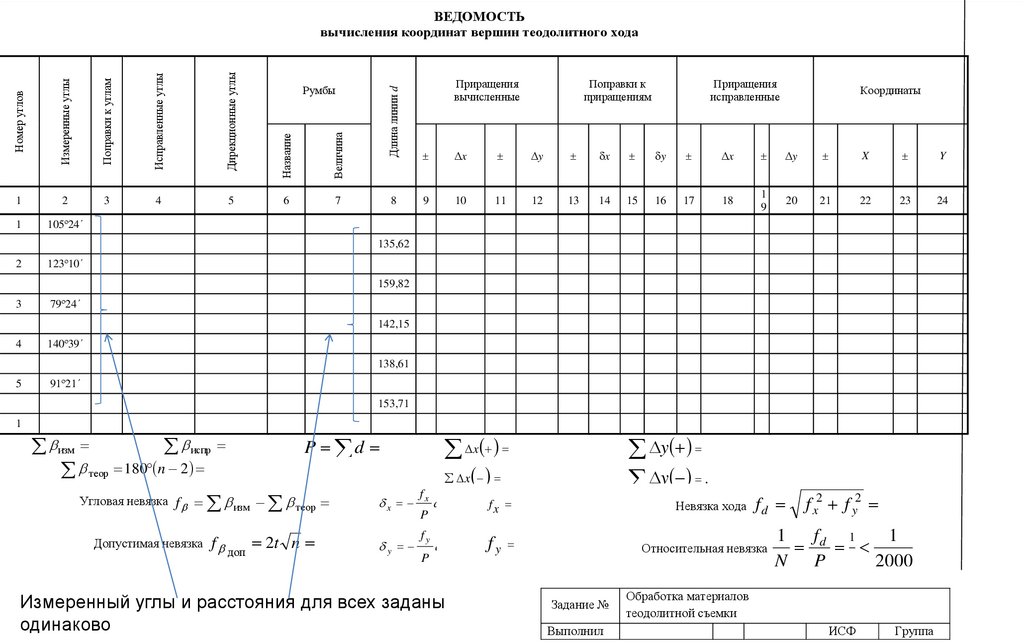
Измеренный углы и расстояния для всех заданы
одинаково
Невязка хода f d
Относительная невязка
Задание №
Выполнил
f x2 f y2
f
1
1
1
d
N P
2000
Обработка материалов
теодолитной съемки
ИСФ
Группа
12.
Исправленные углыДирекционные углы
3
4
5
1
105º24´
6
7
Приращения
вычисленные
Поправки к
приращениям
Приращения
исправленные
Координаты
Длина линии d
Поправки к углам
2
Величина
Измеренные углы
1
Румбы
Название
Номер углов
ВЕДОМОСТЬ
вычисления координат вершин теодолитного хода
x
y
x
y
x
y
X
Y
8
9
10
11
12
13
14
15
16
17
18
1
9
20
21
22
23
24
135,62
2
123º10´
159,82
3
79º24´
142,15
4
140º39´
138,61
5
91º21´
153,71
1
испр
изм
теор 180 n 2
Угловая невязка f
x
изм теор
x
2t n
доп
y
Допустимая невязка f
y
y .
x
P d
fx
d
fx
d
fy
P
fy
P
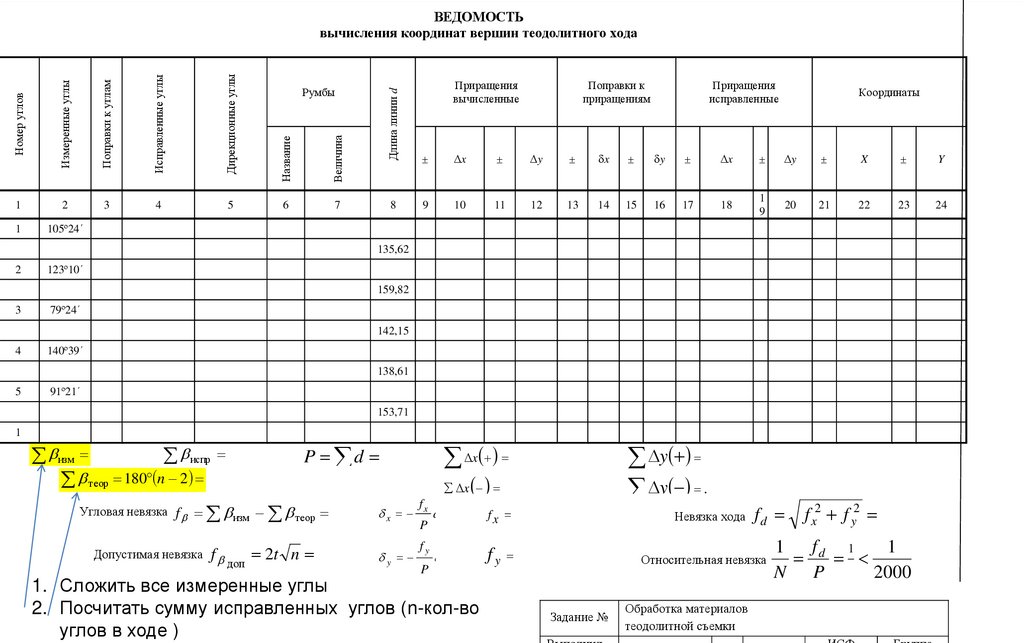
1. Сложить все измеренные углы
2. Посчитать сумму исправленных углов (n-кол-во
углов в ходе )
Невязка хода f d
Относительная невязка
Задание №
Обработка материалов
теодолитной съемки
f x2 f y2
1 fd 1
1
N P
2000
13.
ОБРАБОТКА УГЛОВЫХ ИЗМЕРЕНИЙ.Практические измерения углов сопровождаются ошибками. Величиной
точности теодолитного хода является угловая невязка:
f = Σβ пр – Σβ теор ,
которая не должна превышать определенного предела:
Для замкнутого хода теоретическая сумма внутренних углов равна:
Σβтеор. = 180°(n – 2),
где Σβпр. - сумма углов в замкнутом ходе, полученная в результате хода.
Σβтеор. - теоретическая сумма углов полигона.
n- число углов в полигоне.
Например: в пятиугольном полигоне :
Σβтеор. = 180° (5 – 2) = 540°
Σβп. = 539°58’, отсюда fβпр. =539°58’ – 540° = -2’
Допустимая невязка равна: fβдоп = 1’·√n = 1’√5= 2,2’,
сравниваем невязки и видим, что -2’< 2,2’. Если полученная невязка меньше или равна
допустимой то измерения выполнены правильно.
Производим увязку угловых измерений, т.е. уравниваем полученную сумму измеренных
углов. Для этого в измеренные углы вносим поправки. Поправки вносятся равномерно во все
углы с обратным знаком, т.е. -2’ : 5= 120 ’ ’ : 5= -24 ’ ’
Сумма исправленных углов должна быть равна теоретической сумме углов полигона.
14.
Исправленные углыДирекционные углы
3
4
5
1
105º24´
6
7
Приращения
вычисленные
Поправки к
приращениям
Приращения
исправленные
Координаты
Длина линии d
Поправки к углам
2
Величина
Измеренные углы
1
Румбы
Название
Номер углов
ВЕДОМОСТЬ
вычисления координат вершин теодолитного хода
x
y
x
y
x
y
X
Y
8
9
10
11
12
13
14
15
16
17
18
1
9
20
21
22
23
24
135,62
2
123º10´
159,82
3
79º24´
142,15
4
140º39´
138,61
5
91º21´
153,71
1
изм
испр
теор 180 n 2
Угловая невязка f
x
P d
x
изм теор
x
2t n
доп
y
Допустимая невязка f
fx
d
fx
d
fy
P
fy
P
3. Посчитать угловую невязку.
4. Полученное значение разделить на 5 и данные вписать в ст 3. Невязка всегда
разносится с обратным знаком
5. Посчитать допустимую невязку. Угловая должная быть меньше допустимой
y
y .
Невязка хода f d
Относительная невязка
f x2 f y2
f
1
1
1
d
N P
2000
15.
Исправленные углыДирекционные углы
3
4
5
1
105º24´
6
7
Приращения
вычисленные
Поправки к
приращениям
Приращения
исправленные
Координаты
Длина линии d
Поправки к углам
2
Величина
Измеренные углы
1
Румбы
Название
Номер углов
ВЕДОМОСТЬ
вычисления координат вершин теодолитного хода
x
y
x
y
x
y
X
Y
8
9
10
11
12
13
14
15
16
17
18
1
9
20
21
22
23
24
135,62
2
123º10´
159,82
3
79º24´
142,15
4
140º39´
138,61
5
91º21´
153,71
1
изм
теор 180 n 2
Угловая невязка f
x
P d
испр
x
изм теор
x
2t n
доп
y
Допустимая невязка f
fx
d
fx
d
fy
P
fy
P
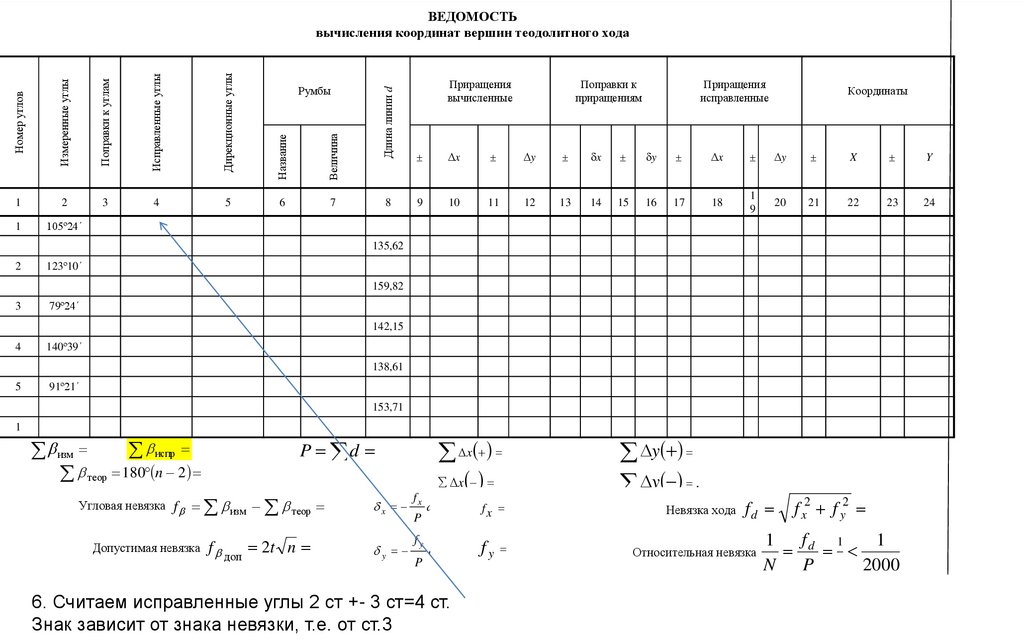
6. Считаем исправленные углы 2 ст +- 3 ст=4 ст.
Знак зависит от знака невязки, т.е. от ст.3
y
y .
Невязка хода f d
Относительная невязка
f x2 f y2
f
1
1
1
d
N P
2000
16.
Исправленные углыДирекционные углы
3
4
5
1
105º24´
6
7
задано
2
Приращения
вычисленные
Поправки к
приращениям
Приращения
исправленные
Координаты
Длина линии d
Поправки к углам
2
Величина
Измеренные углы
1
Румбы
Название
Номер углов
ВЕДОМОСТЬ
вычисления координат вершин теодолитного хода
x
y
x
y
x
y
X
Y
8
9
10
11
12
13
14
15
16
17
18
1
9
20
21
22
23
24
135,62
123º10´
159,82
3
79º24´
142,15
4
140º39´
138,61
5
91º21´
153,71
1
изм
теор 180 n 2
Угловая невязка f
x
P d
испр
x
изм теор
x
2t n
доп
y
Допустимая невязка f
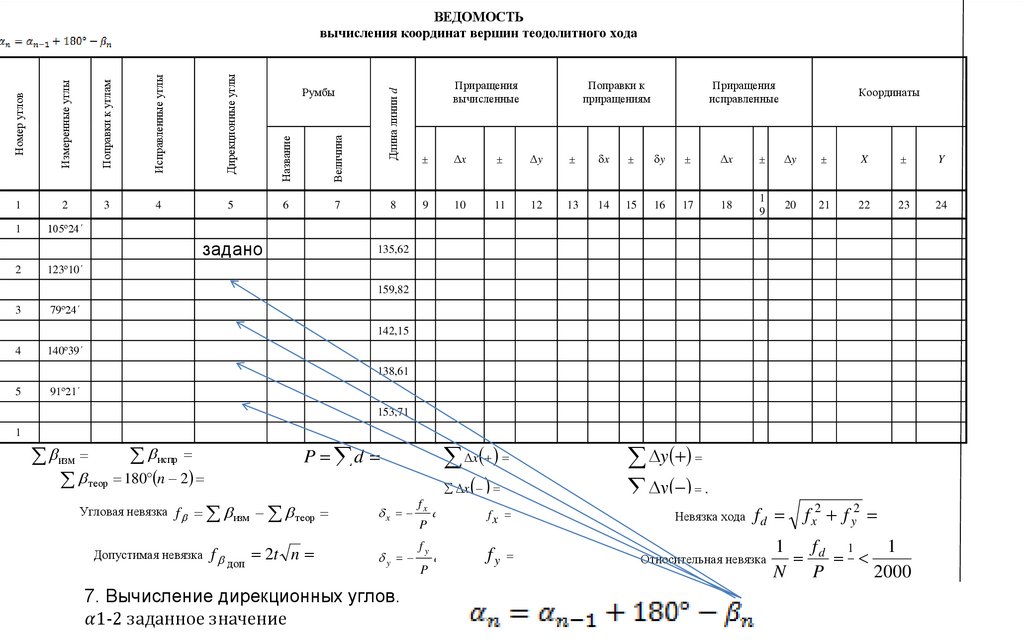
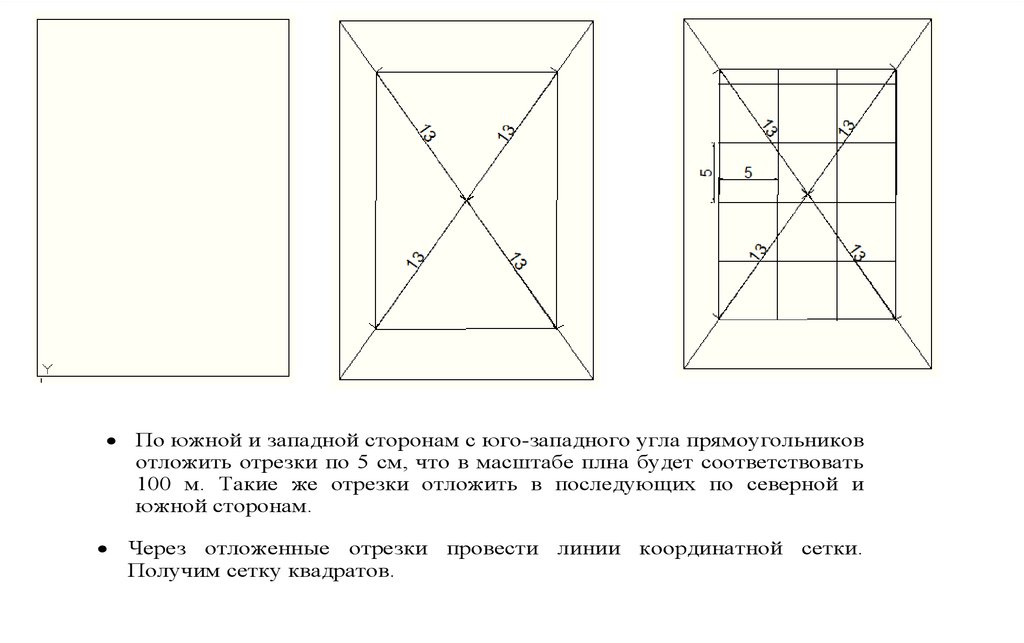
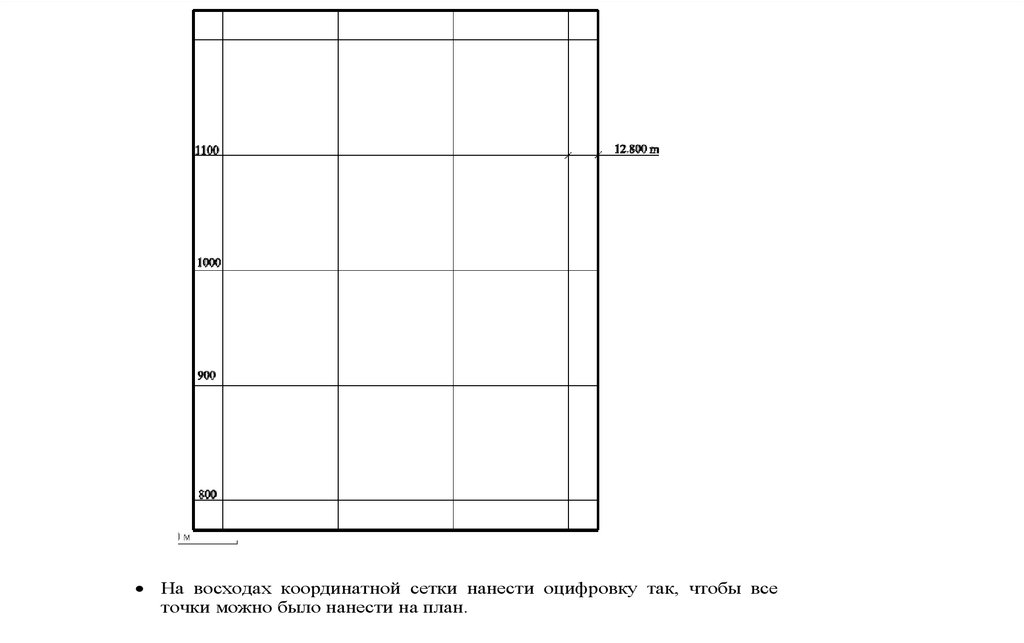
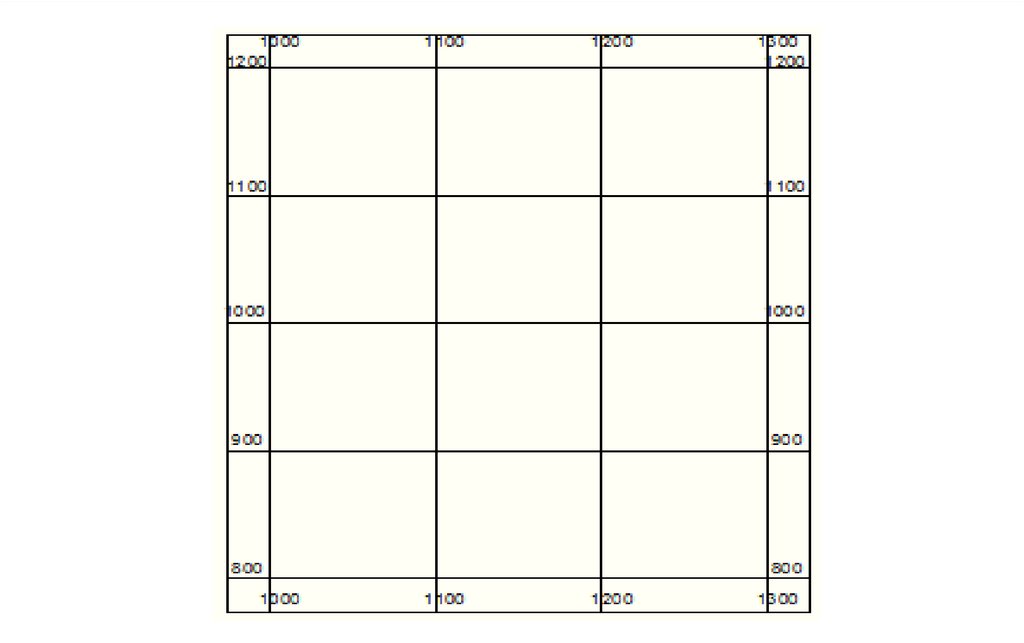
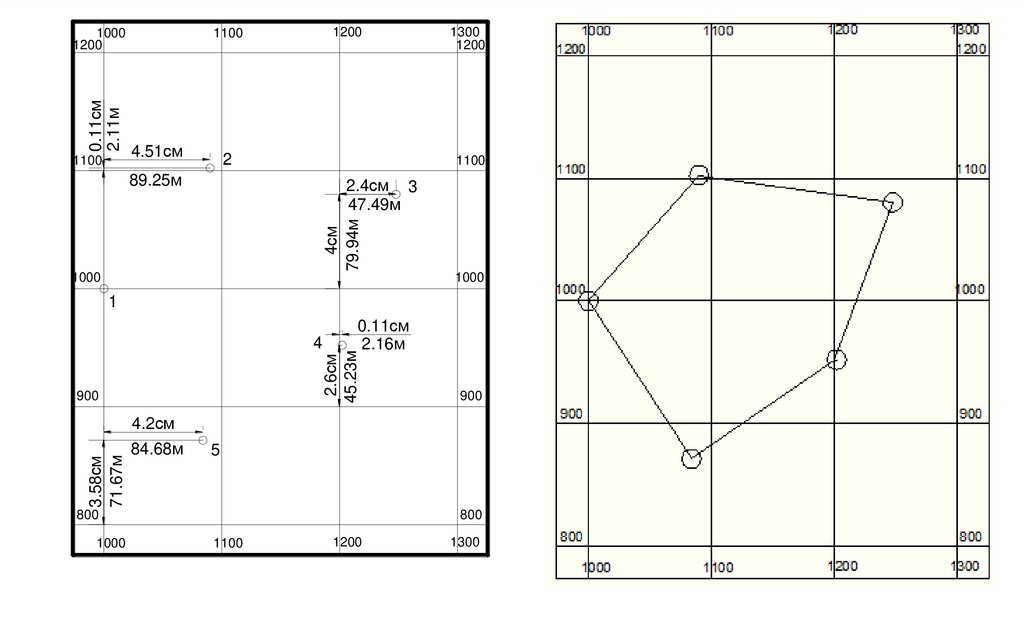
7. Вычисление дирекционных углов.













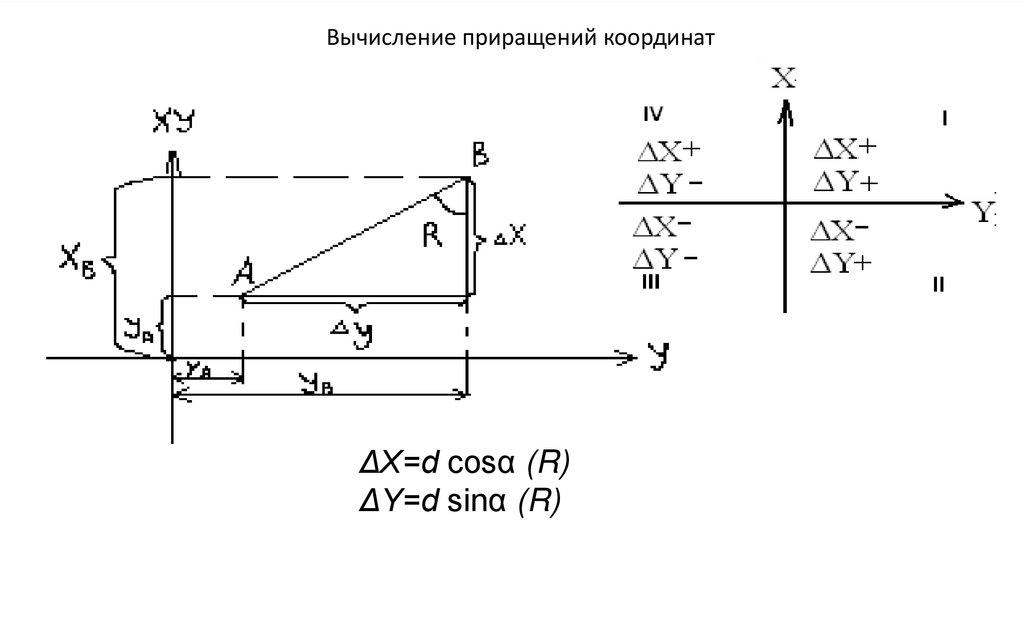

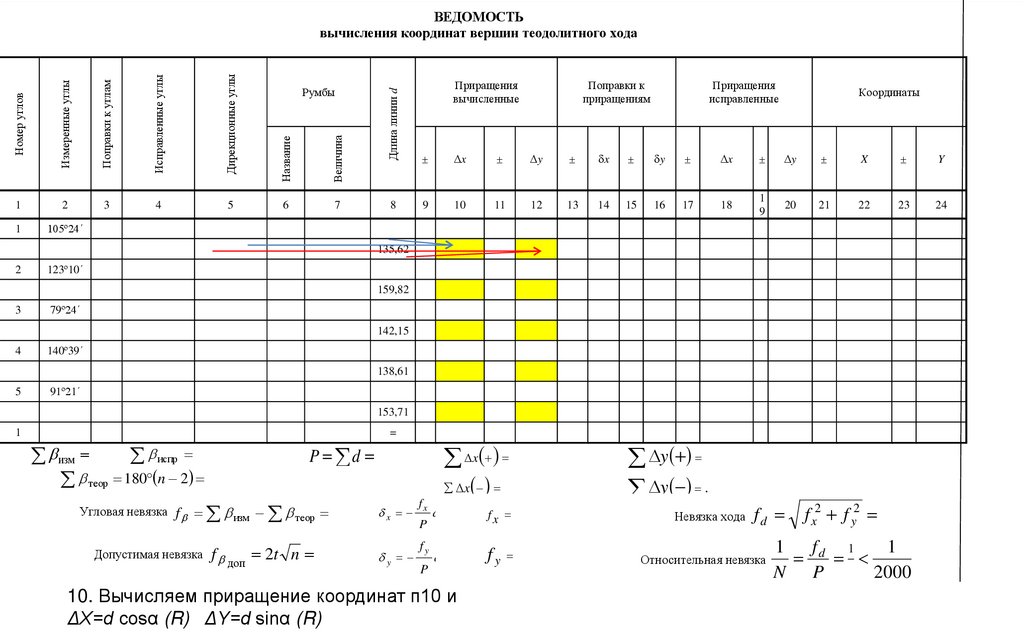
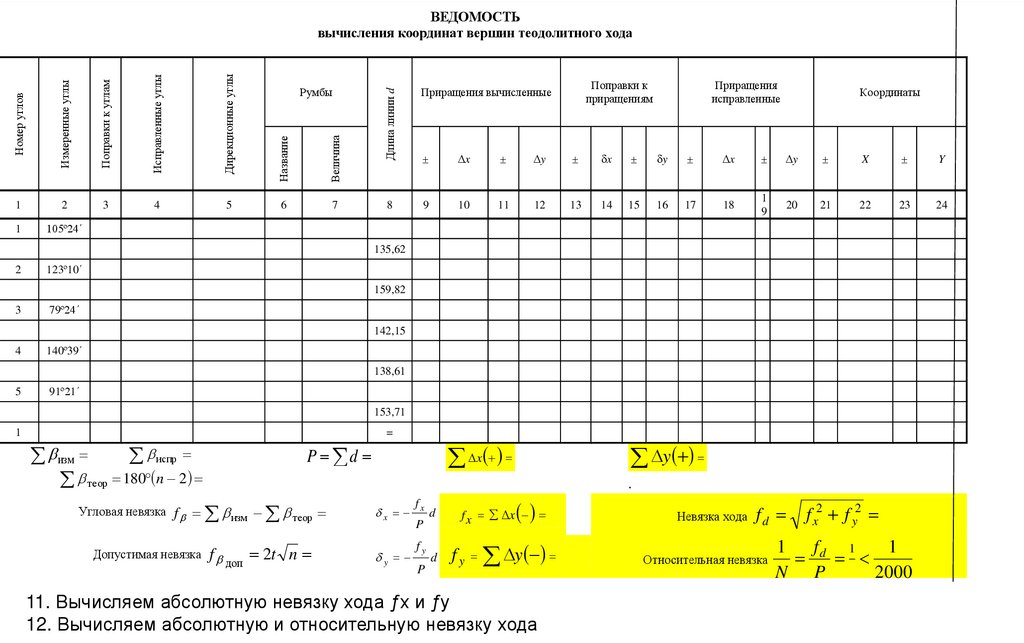
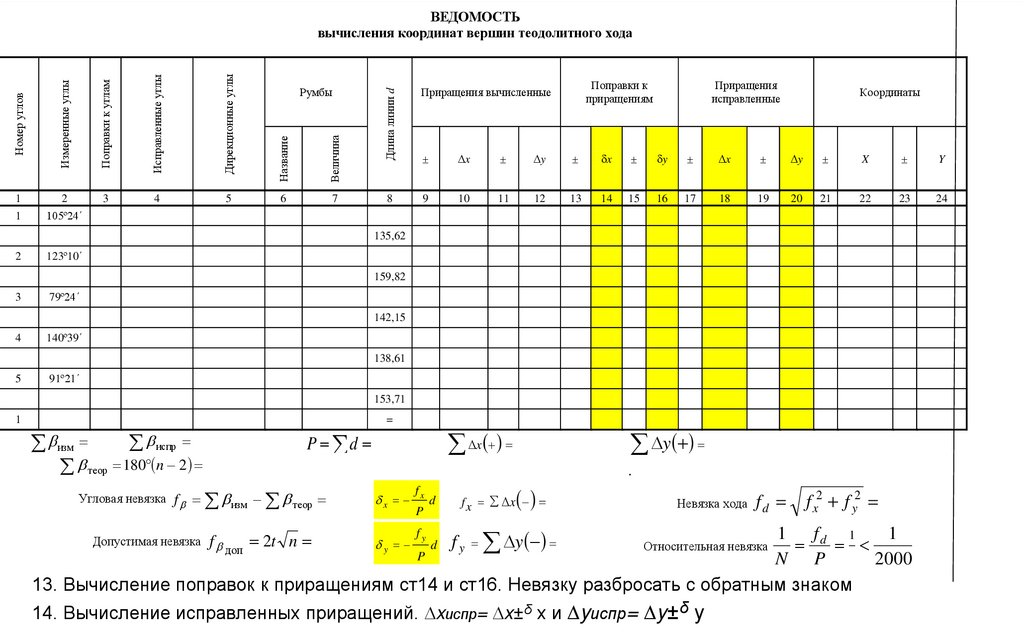









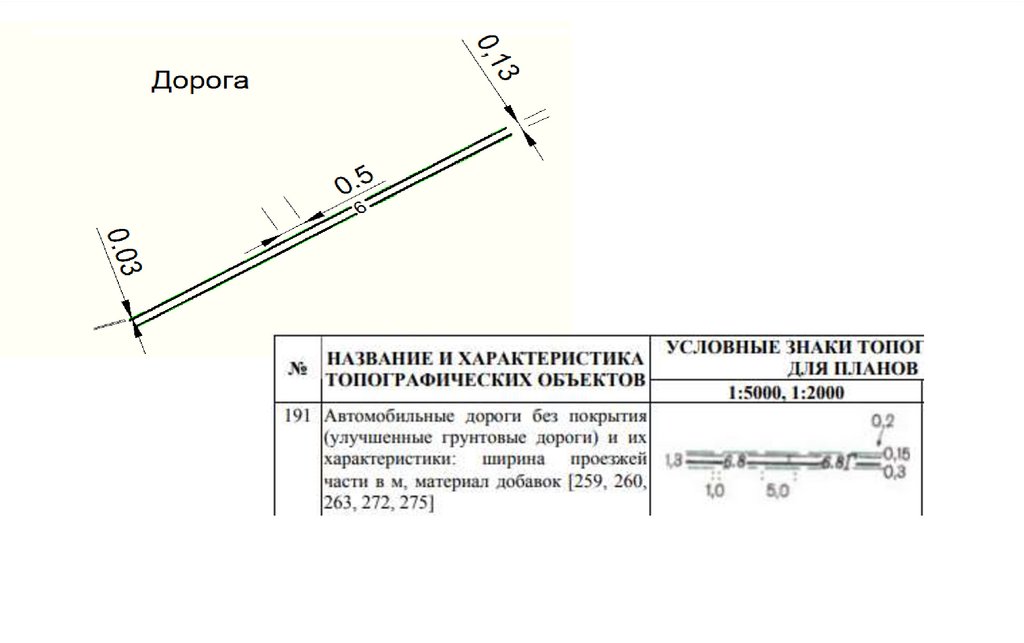



 geography
geography








