Similar presentations:
Решение задач математической физики численными методами
1.
Министерство науки и высшего образования Российской ФедерацииФедеральное государственное бюджетное образовательное учреждение
высшего образования «Московский государственный технический университет
имени Н.Э. Баумана (национальный исследовательский университет)»
(МГТУ им. Н.Э. Баумана)
Факультет: Фундаментальные науки
Кафедра: Высшая математика
РЕШЕНИЕ ЗАДАЧ
МАТЕМАТИЧЕСКОЙ ФИЗИКИ
ЧИСЛЕННЫМИ МЕТОДАМИ
(курсовая работа)
Выполнила
Сытник В.А. ФН1-61Б
Руководитель
курсовой работы
Консультант
А.А Федотов
П.В. Храпов
2.
СОДЕРЖАНИЕ1. Введение
2. Описание МКЭ
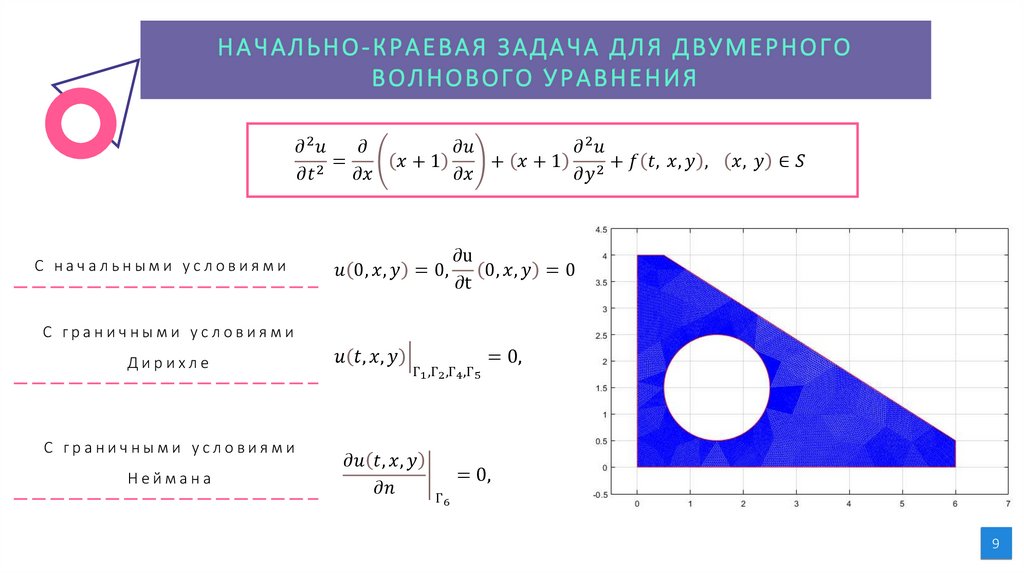
3. Начально-краевая модельная задача для
двумерного волнового уравнения
4. Начально-краевая задача для двумерного
волнового уравнения
5. Заключение
6. Список использованных источников
2
3.
В В ЕДЕНИЕВ прикладных проблемах многие задачи математической физики
приводят к дифференциальным уравнениям с частными
производными. Подавляющее число базовых уравнений
математической физики решается с помощью численных методов
путем построения корректной математической модели. В настоящее
время появилось значительное число различных программных
продуктов, с помощью которых, задавая только входные данные,
можно решить значительное число задач.
33
4.
ЦЕЛЬ:Научиться решать дифференциальные уравнения в
частных производных с помощью программных
с р е д с т в M AT L A B .
ЗАДАЧИ:
1) Ознакомиться с методом конечных элементов и
техникой его применения.
2) Ознакомиться с инструментом PDE toolbox
с и с т е м ы M AT L A B
3) Численно решить задачу PDE, т.е. сгенерировать
сетки, дискретизировать уравнения и получить
приближение к решению.
44
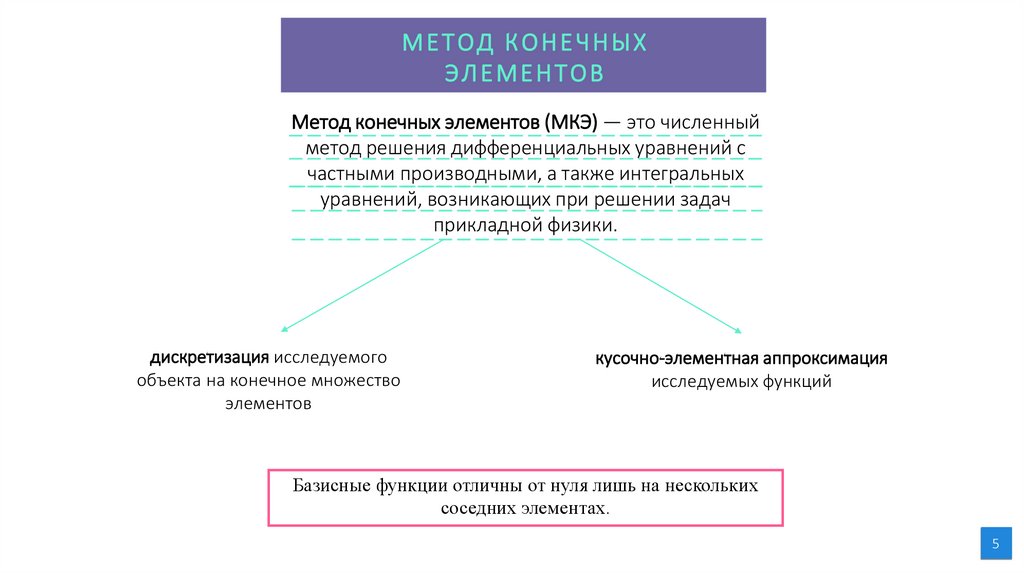
5.
МЕТОД КОНЕЧНЫХЭЛЕМЕНТОВ
Метод конечных элементов (МКЭ) — это численный
метод решения дифференциальных уравнений с
частными производными, а также интегральных
уравнений, возникающих при решении задач
прикладной физики.
дискретизация исследуемого
объекта на конечное множество
элементов
кусочно-элементная аппроксимация
исследуемых функций
Базисные функции отличны от нуля лишь на нескольких
соседних элементах.
55
6.
Характерные черты МКЭ:1) расчетная
область
разбивается
на
конечное
функционал;
число










 mathematics
mathematics physics
physics








