Множества. Понятие множества, его элементы

1.

Классная работа
Множества
1. Понятие множества, его элементы.
2. Операции над множествами.
«Высшее назначение математики состоит в том, чтобы
находить скрытый порядок в хаосе, который нас окружает».
Н. Винер

2.

Георг Кантор
Георг Кантор (нем. Georg
Ferdinand Ludwig Philipp Cantor),
Кантор считается основателем
теории множеств и сделал
большой вклад в современную
математику.

3.

Галилео Галилей
(15.02.1564 – 08.01.1642)
«Великая книга
Природы
написана языком
математики»

4.

Леонард Эйлер
4 апреля 1707, Базель, Швейцария —
7 сентября 1783, Санкт-Петербург, Россия),
выдающийся математик, внёсший
значительный вклад в развитие
математики, а также механики, физики,
астрономии и ряда прикладных наук.

5.

Понятие множества
В повседневной жизни постоянно различные
совокупности предметов называют одним словом.
Например:
Совокупность документов – архив
Собрание музыкантов – оркестр
Группа лошадей – табун
Большая группа людей – толпа
Родители, дети и их родственники – семья
Собрание книг – библиотека

6.

Примеры множеств
• Множество всех людей, живущих в настоящее время на Земле.
• Множество звезд в Галактике.
• Множество всех натуральных чисел.
• Множество учеников 9 А класса.
• Множество учеников 9 А класса, не выполнивших домашнее
задание по алгебре.
• Множество президентов РФ.
• Множество точек плоскости, равноудаленных от данной точки.
• Множество всех рыб в Тихом океане.

7.

Математическое множество
Математическое
понятие,
отражающее
объединение некоторых объектов, предметов или
понятий в единую совокупность, является
понятием множества.
Это понятие в математике является первичным,
не определяемым, таким же, как понятие точки и
прямой в геометрии, – к более простым понятиям оно
не сводится.

8.

Примеры математических множеств
• Множество всех натуральных чисел.
• Множество точек плоскости, равноудаленных от
данной точки.
• Корни уравнения х2 + 10х = 39.
• Множество всех двухзначных чисел, кратных 3.
• Множество цифр.
• Приведите свои примеры.

9.

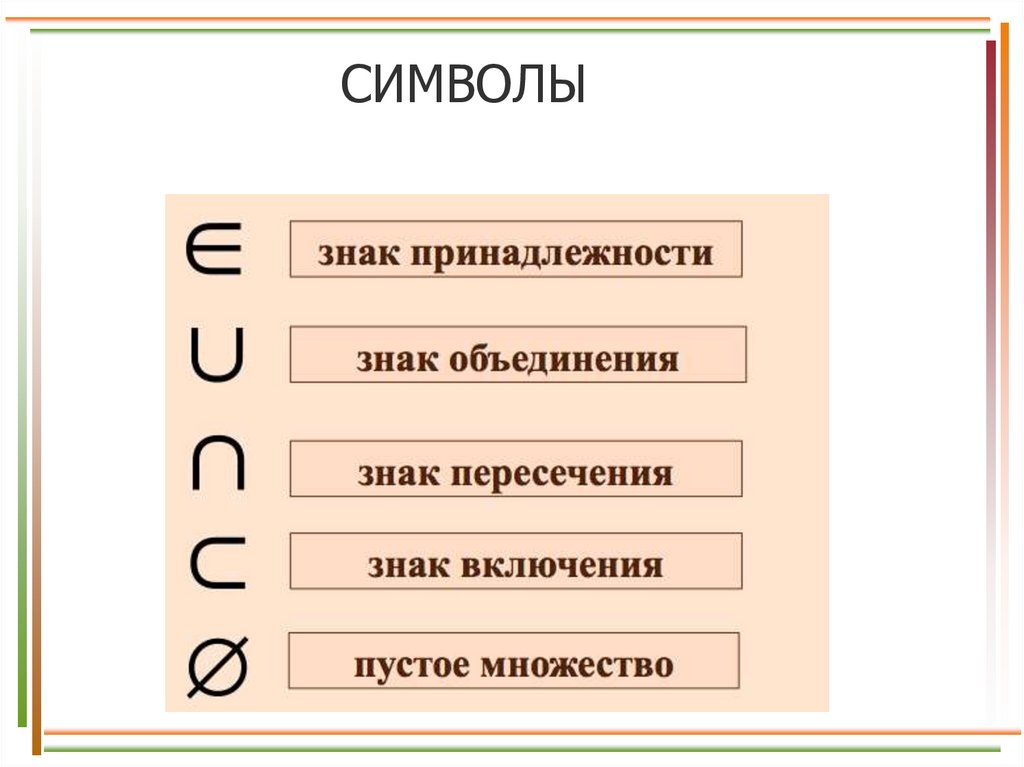
СИМВОЛЫ

10.

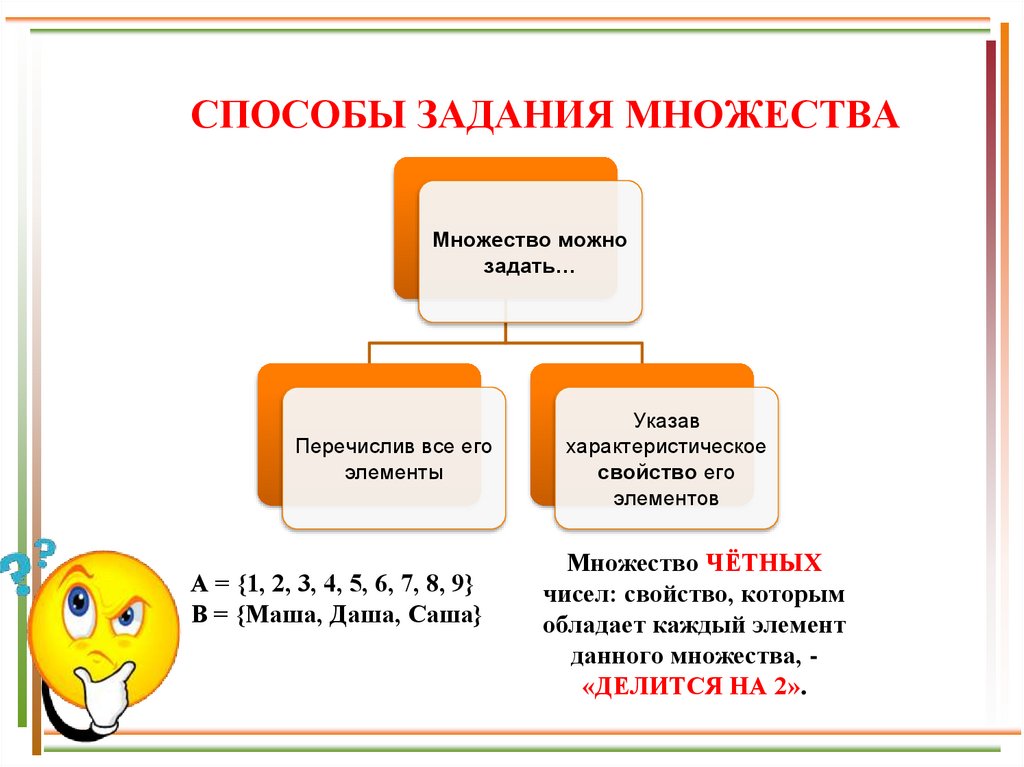
СПОСОБЫ ЗАДАНИЯ МНОЖЕСТВА
Множество можно
задать…
Перечислив все его
элементы
А = {1, 2, 3, 4, 5, 6, 7, 8, 9}
B = {Маша, Даша, Саша}
Указав
характеристическое
свойство его
элементов
Множество ЧЁТНЫХ
чисел: свойство, которым
обладает каждый элемент
данного множества, «ДЕЛИТСЯ НА 2».

11.

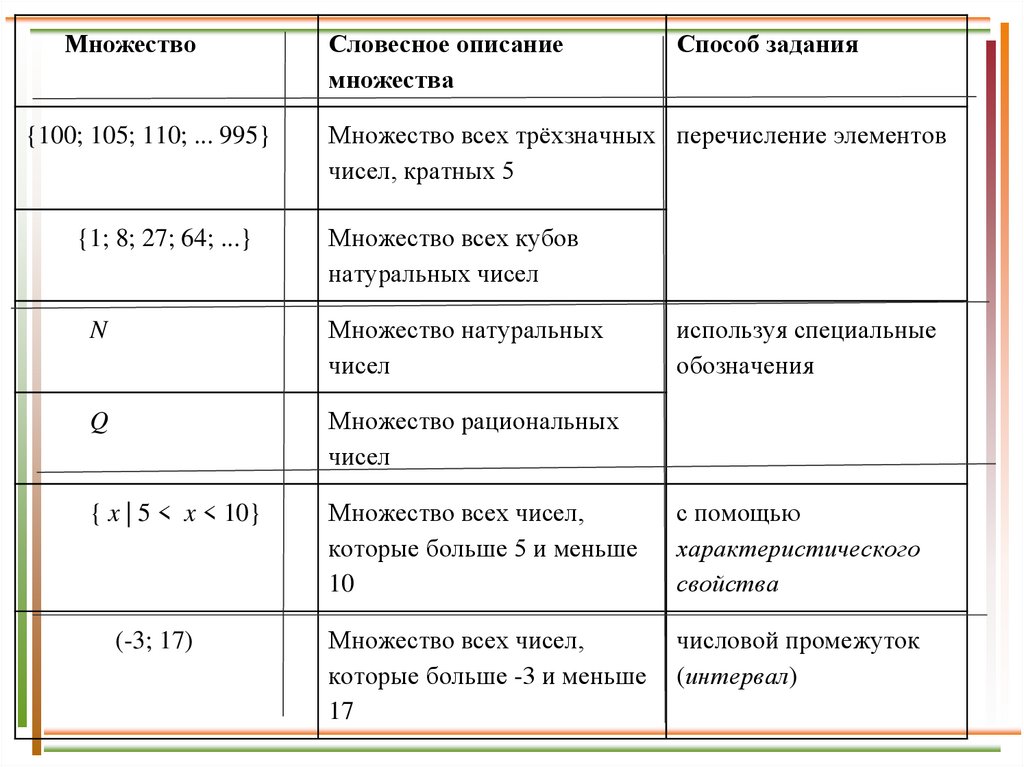
Множество
{100; 105; 110; ... 995}
Словесное описание
множества
Способ задания
Множество всех трёхзначных перечисление элементов
чисел, кратных 5
{1; 8; 27; 64; ...}
Множество всех кубов
натуральных чисел
N
Множество натуральных
чисел
Q
Множество рациональных
чисел
{ x | 5 < x < 10}
Множество всех чисел,
которые больше 5 и меньше
10
с помощью
характеристического
свойства
Множество всех чисел,
которые больше -3 и меньше
17
числовой промежуток
(интервал)
(-3; 17)
используя специальные
обозначения

12.

РАВНЫЕ МНОЖЕСТВА это множества, состоящие из одних
и тех же элементов

13.

Подмножество
Если каждый элемент множества В является
элементом множества А, то множество В
называют подмножеством множества А.
В⊂А
Знак ⊂ называется включением
С
А
В
В⊂А

14.

А = {a, b, c}
ЧИСЛОВЫЕ
МНОЖЕСТВА

15.

ОПЕРАЦИИ НАД МНОЖЕСТВАМИ
• разность множеств
• пересечение
• объединение

16.

17.

18.

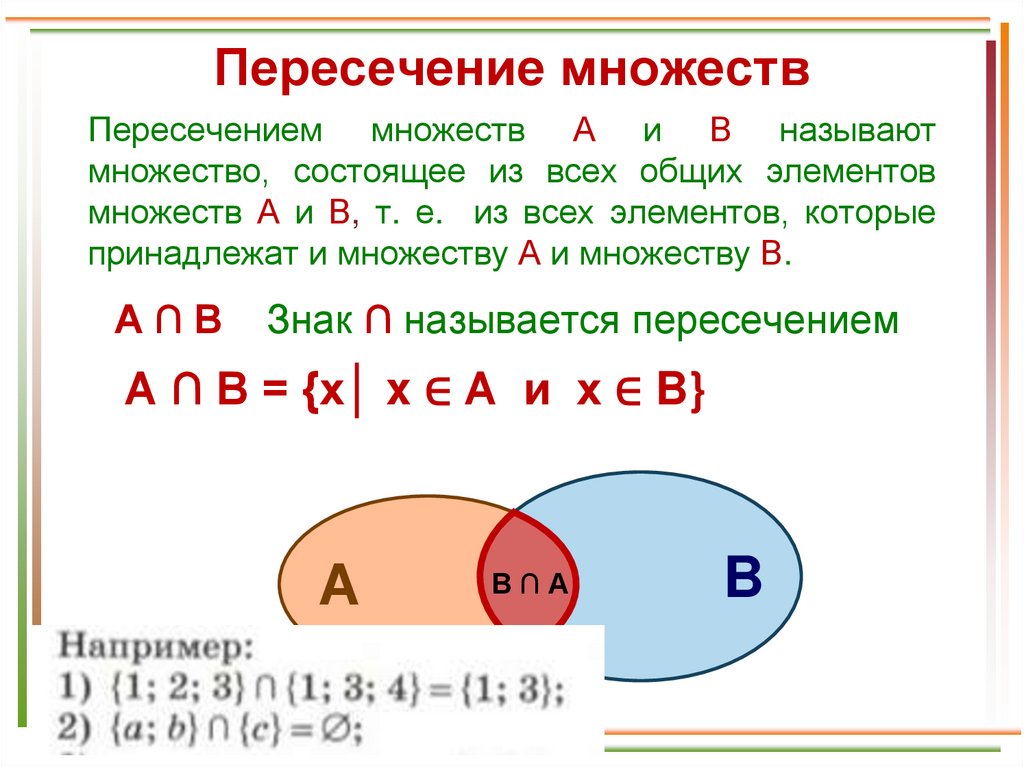
Пересечение множеств
Пересечением множеств А и В называют
множество, состоящее из всех общих элементов
множеств А и В, т. е. из всех элементов, которые
принадлежат и множеству А и множеству В.
А∩В
Знак ∩ называется пересечением
А ∩ В = {x│ x ∈ A и x ∈ B}
А
В∩А
B

19.

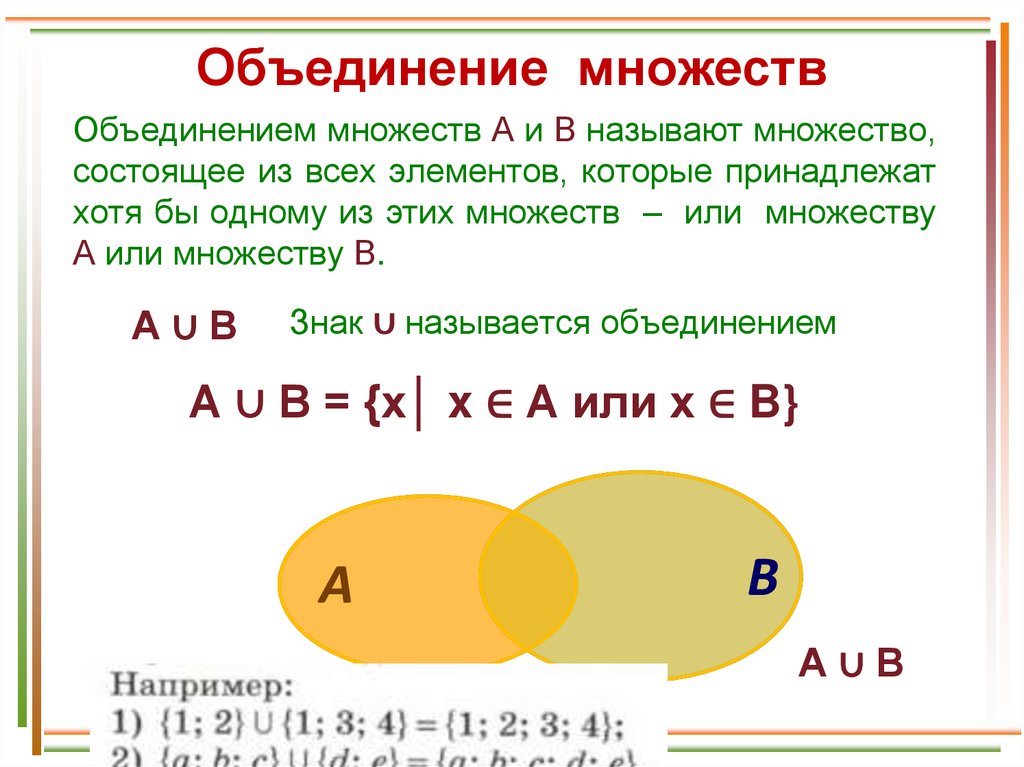
Объединение множеств
Объединением множеств А и В называют множество,
состоящее из всех элементов, которые принадлежат
хотя бы одному из этих множеств – или множеству
А или множеству В.
А∪В
Знак ∪ называется объединением
А ∪ В = {x│ x ∈ A или x ∈ B}
А
B
А∪В

20.

УСТНО:
М = {2, 4, 6, 8}
Верно ли:

21.

РЕФЛЕКСИЯ