Similar presentations:
Выполнение практической работы №4 по информатике
1.
РГУ НЕФТИ И ГАЗА (НИУ) ИМЕНИ И.М. ГУБКИНАКафедра: Информатики
Презентация
по выполненному практической части
домашнего задания №4
Выполнила:
студентка группы ААМ-21-07
Ущеко Анфиса Валерьевна
Москва, 2023
2.
Домашнее задание 4Для произвольного изображения:
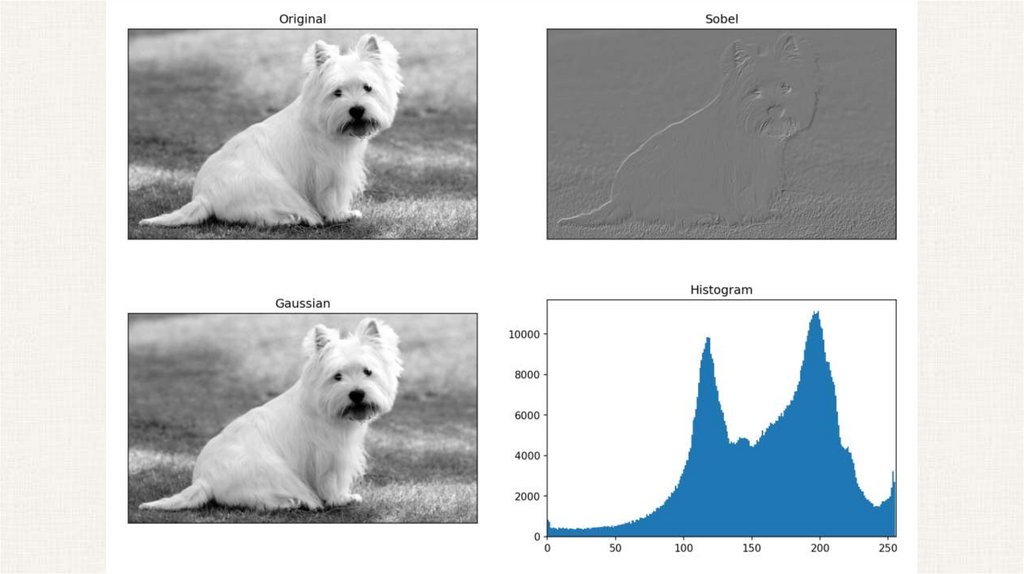
1. Определить границы с использованием операторов Собеля и Гаусса,
сравнить результаты и сделать вывод, построить гистограммы.
2. Определить количество углов на изображении с помощью детектора
Харриса и любым другим детектором. Сравнить результаты.
3. Определить количество объектов на изображении с помощью
функции Label.
4. Наложить на изображение углы Харриса, центры масс объектов и
области SIFT (используя разные цвета).
3.
Оператор Собеля• Оператор Собеля — дискретный дифференциальный оператор, вычисляющий
приближённое значение градиента яркости изображения.
• Оператор Собеля основан на свёртке изображения небольшими сепарабельными
целочисленными фильтрами в вертикальном и горизонтальном направлениях,
поэтому его относительно легко вычислять. С другой стороны, используемая
им аппроксимация градиента достаточно грубая, особенно это сказывается на
высокочастотных колебаниях изображения.
• Оператор вычисляет градиент яркости изображения в каждой точке. Так находится
направление наибольшего увеличения яркости и величина её изменения в этом
направлении. Результат показывает, насколько «резко» или «плавно» меняется
яркость изображения в каждой точке, а значит, вероятность нахождения точки на
грани, а также ориентацию границы. На практике вычисление величины
изменения яркости (вероятности принадлежности к грани) надёжнее и проще в
интерпретации, чем расчёт направления.
4.
Оператор Собеля# оператор Собеля для определения границ
sobelx = cv2.Sobel(img, cv2.CV_64F, 1, 0, ksize=5)
sobely = cv2.Sobel(img, cv2.CV_64F, 0, 1, ksize=5)
sobel = cv2.addWeighted(sobelx, 0.5, sobely, 0.5, 0)
5.
Фильтр Гаусса• Фильтр Гаусса - это фильтр нижних частот, используемый для
уменьшения
шума
(высокочастотных
составляющих)
и
размывания областей изображения. Фильтр реализован в виде
симметричного ядра нечетного размера (DIP-версия матрицы),
которое пропускается через каждый пиксель интересующей
области для получения желаемого эффекта. Ядро не сильно
подвержено резкому изменению цвета (края) из-за того, что
пиксели, расположенные ближе к центру ядра, имеют больший
вес по отношению к конечному значению, чем к периферии.
6.
Фильтр Гаусса# фильтр Гаусса для уменьшения
шума
gaussian = cv2.GaussianBlur(img,
(5, 5), 0)
7.
8.
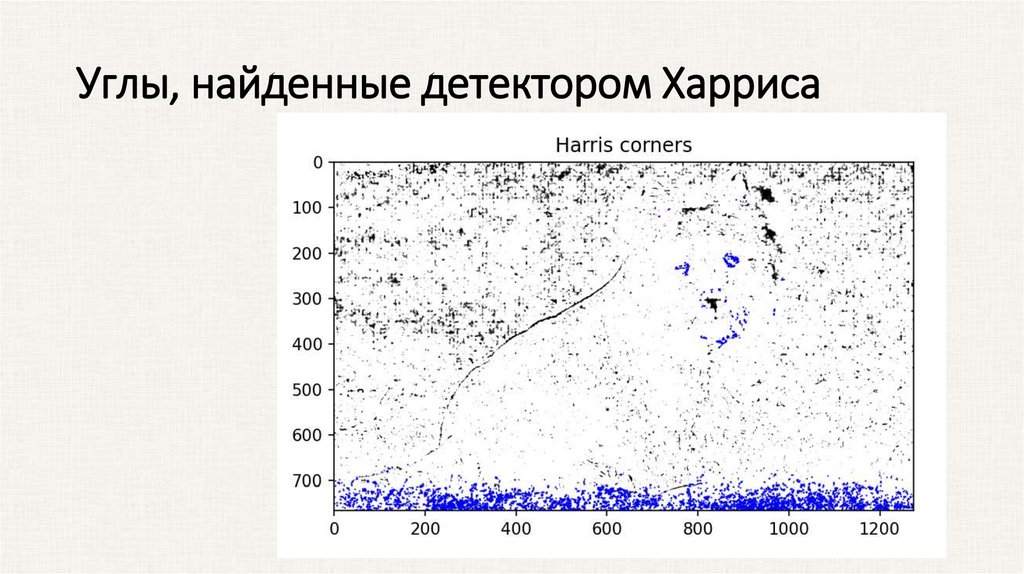
Детектор Харриса• Алгоритм проверяет каждый пиксель в изображении, проверяя:
является ли он углом, рассматривая некоторую его окрестность.
Вводится анизотропия по всем направлениям.
• В данном алгоритме вычисляются производные яркости
изображения для исследования изменений яркости по множеству
направлений. Они вводят в рассмотрение производные по
некоторым принципиальным направлениям.
• Основная идея состоит в том, для каждого пикселя изображения
вычисляется значение особой функции отклика угла,
оценивающая степень похожести изображения окрестности точки
на угол.
9.
Углы, найденные детектором Харриса10.
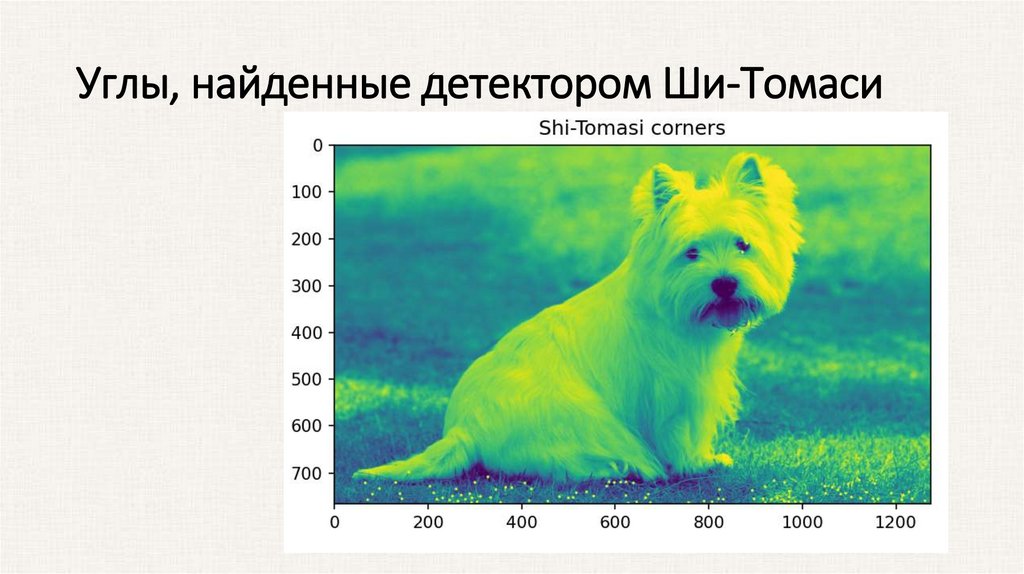
Детектор Ши-ТомасиУгловой детектор Ши-Томаси (Shi-Tomasi или Kanade-Tomasi, 1993)
во многом совпадает с детектором Харриса, но различается в
вычислении меры отклика: алгоритм напрямую вычисляет
значение, поскольку делается предположение, что поиск углов
будет более стабильным. Авторы используют это же уравнение для
анализа оптического потока Лукаса и Канаде (Lucas and Kanade).
11.
Углы, найденные детектором Ши-Томаси12.
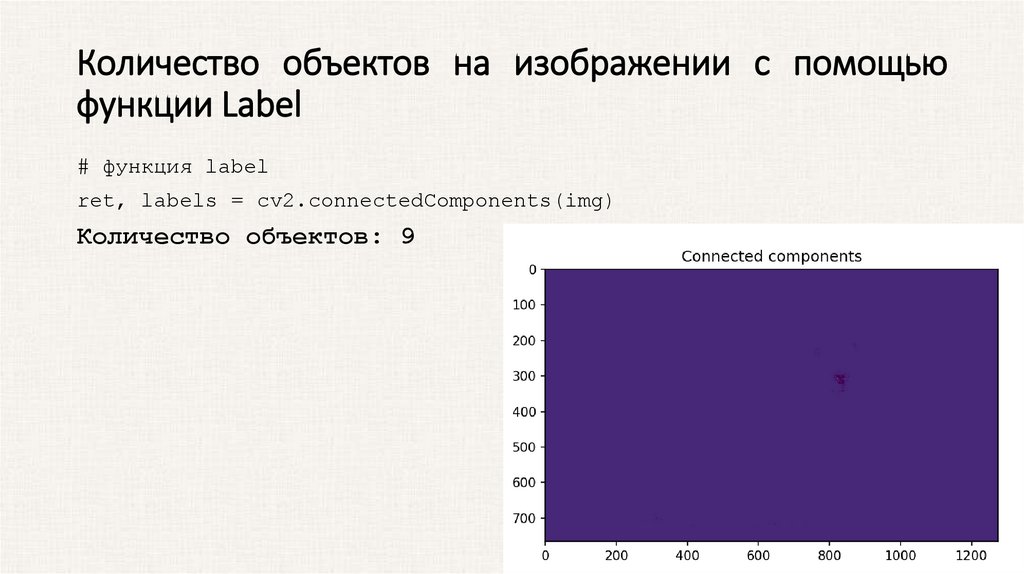
Количество объектов на изображении с помощьюфункции Label
# функция label
ret, labels = cv2.connectedComponents(img)
Количество объектов: 9
13.
Определение центров масс объектов с помощьюпороговой бинаризации
gray = cv2.convertScaleAbs(gray)
thresh = cv2.adaptiveThreshold(gray, 255,
cv2.ADAPTIVE_THRESH_GAUSSIAN_C, cv2.THRESH_BINARY, 11, 2)
contours, _ = cv2.findContours(thresh, cv2.RETR_EXTERNAL,
cv2.CHAIN_APPROX_SIMPLE)
centers = []
for contour in contours:
M = cv2.moments(contour)
if M["m00"] != 0:
cX = int(M["m10"] / M["m00"])
cY = int(M["m01"] / M["m00"])
centers.append((cX, cY))
14.
Наложить на изображение углы Харриса,центры масс объектов и области SIFT
# Детекция SIFT-особенностей
sift = cv2.SIFT_create()
kp = sift.detect(gray, None)
img = cv2.drawKeypoints(img, kp, img,
flags=cv2.DRAW_MATCHES_FLAGS_DRAW_RICH_KEYPOINTS)
# Отрисовка углов Харриса красным цветом
img[harris > 0.01 * harris.max()] = [0, 0, 255]
# Отрисовка центров масс объектов зеленым цветом
for center in centers:
cv2.circle(img, center, 5, (0, 255, 0), -1)
# Отрисовка областей SIFT голубым цветом
img = cv2.drawKeypoints(img, kp, None, color=(255, 0, 0))












 informatics
informatics