Методы поиска. Лекция 3

1.

Алгоритмы и
структуры
данных
• Модуль 2. Методы поиска.
• Лекция 3. Хеширование. Поиск хешированием.

2.

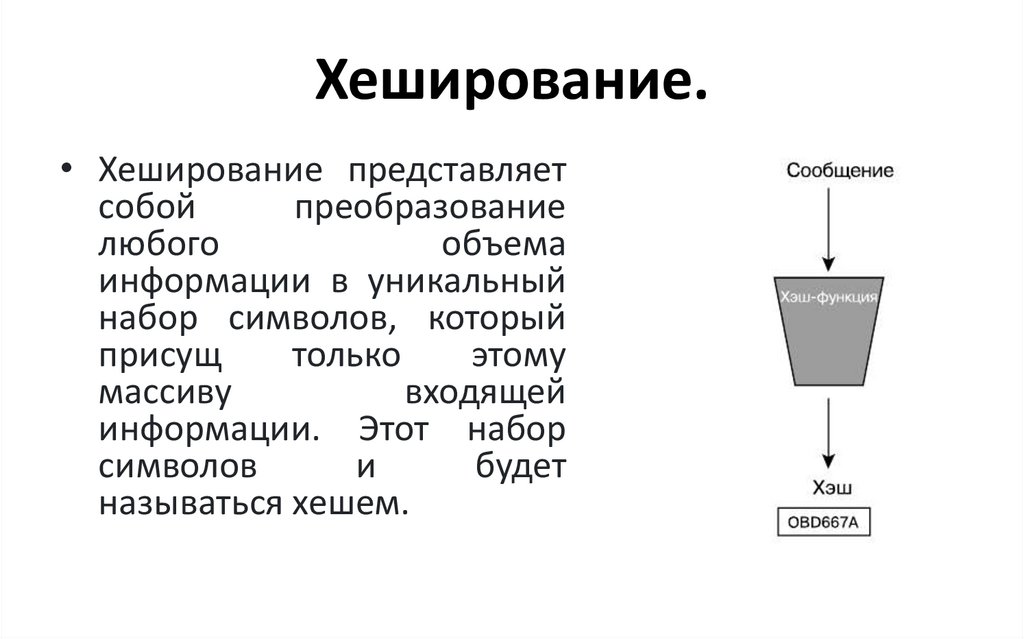
Хеширование.
• Хеширование представляет
собой
преобразование
любого
объема
информации в уникальный
набор символов, который
присущ
только
этому
массиву
входящей
информации. Этот набор
символов
и
будет
называться хешем.

3.

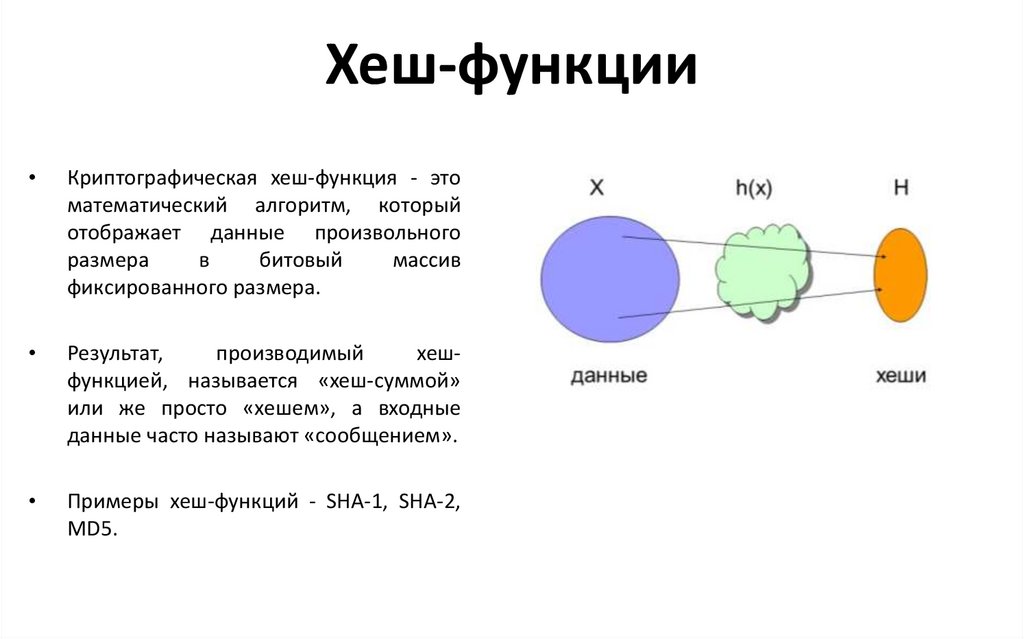
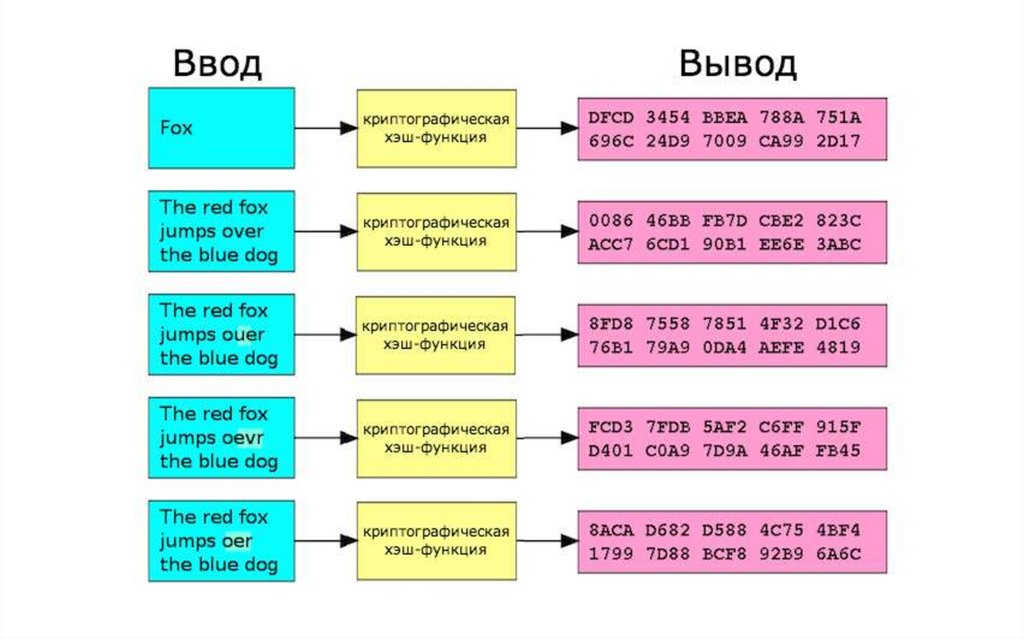
Хеш-функции
Криптографическая хеш-функция - это
математический алгоритм, который
отображает данные произвольного
размера
в
битовый
массив
фиксированного размера.
Результат,
производимый
хешфункцией, называется «хеш-суммой»
или же просто «хешем», а входные
данные часто называют «сообщением».
Примеры хеш-функций - SHA-1, SHA-2,
MD5.

4.

Хеш-функции (Свойства)
Хеш всегда уникален для каждого массива информации. Однако иногда случаются так называемые
коллизии, когда для разных входных блоков информации вычисляются одинаковые хеш-коды.
При самом незначительном изменении входной информации ее хеш полностью меняется.
Хеш-функция необратима и не позволяет восстанавливать исходный массив информации из символьной
строки. Это можно сделать, только перебрав все возможные варианты, что при бесконечном количестве
информации требует много времени и денег.
Хеширование позволяет достаточно быстро вычислить нужный хеш для достаточно большого объема
информации.
Алгоритм работы хеш-функции, как правило, делается открытым, чтобы при необходимости можно было
оценить ее стойкость к восстановлению начальных данных по выдаваемому хешу.
Хеш-функция должна уметь приводить любой объем данных к числу заданной длины.

5.

6.

Области применения хеширования
• Работа с большими объемами
информации
• Проверка целостности данных при
передаче
• Шифрование
• Электронные цифровые подписи
• Хранение паролей

7.

Для идеальной хеш-функции
выполняются следующие
условия:
• Хеш-функция является детерминированной̆, то
есть одно и то же сообщение приводит к одному и
тому же хеш-значению.
• Значение хеш-функции быстро вычисляется для
любого сообщения.
• Невозможно найти сообщение, которое дает
заданное хеш-значение.
• Невозможно найти два разных сообщения с
одинаковым хеш-значением.
• Небольшое изменение в сообщении изменяет
хеш настолько сильно, что новое и старое
значения кажутся не коррелирующими.

8.

Поиск хешированием
В основе поиска лежит переход от исходного
множества к множеству
хэш–функций h(k).
функция имеет следующий вид:
Хеш–
Множество хеш–функций состоит из нулей;
h(k) = k mod (m),
где:
Пусть m = 1, тогда h(k) = {0, 0, 0, 0, 0, 0};
Пусть m = 20, тогда
h(k) = {9, 1, 4, 10, 8, 5};
k – ключ;
Множество хеш–функций повторяет
m – целое число;
исходное множество;
mod – остаток от целочисленного деления.
Например, пусть дано множество {9, 1, 4, 10, 8, 5}.
Определим для него хеш–функцию h(k)= k mod m;
Пусть m равно половине максимального
ключа m = [Kmax/2], тогда
h(k) = {4, 1, 4, 0, 3, 0};
m = [10/2] = 5;

9.

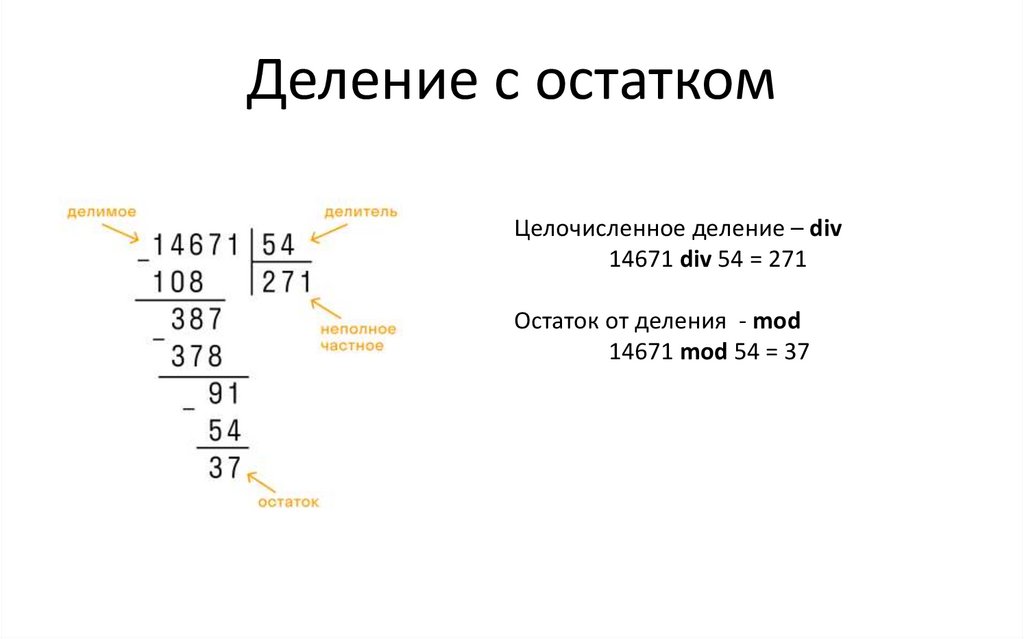
Деление с остатком
Целочисленное деление – div
14671 div 54 = 271
Остаток от деления - mod
14671 mod 54 = 37

10.

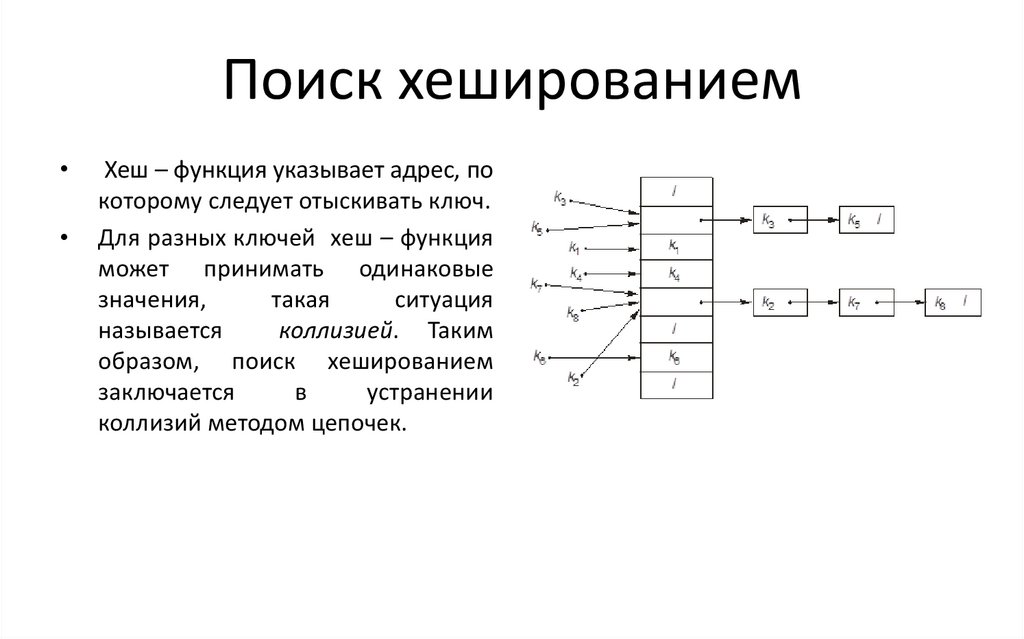
Поиск хешированием
Хеш – функция указывает адрес, по
которому следует отыскивать ключ.
Для разных ключей хеш – функция
может принимать одинаковые
значения,
такая
ситуация
называется
коллизией. Таким
образом, поиск хешированием
заключается
в
устранении
коллизий методом цепочек.

11.

Коллизии хеш-функций
• Коллизия хеш-функции — это
когда у двух разных входных
элементов таблицы хеш будет
одинаковым.
Коллизии
встречаются в разнообразных
алгоритмах хеширования, однако
это не является нормой и в
«правильных»
алгоритмах
их
возникновение
сведено
к
минимальному значению. Но в то
же время, когда приходится
работать с большими таблицами
хеширования, то их возникновение
неизбежно.

12.

Поиск хешированием (пример 1)
Дано множество ключей:
{7, 13, 6, 3, 9, 4, 8, 5}.
Найти ключ K = 27. Хеш – функция равна h(k) = K mod m;
m = [13/2] = 6 (т.к. 13 – максимальный ключ);
h(k) = {1, 1, 0, 3, 3, 4, 2, 5}.
Для устранения коллизий построим построим таблицу:
Попарным сравнением множества хеш–функций и множества
исходных ключей, заполняем таблицу. При этом хеш–функция
указывает адрес, по которому следует отыскивать ключ.
Например , если отыскивается ключ K = 27, тогда h(k) = 27 mod 6=3
- это значит, что ключ K = 27 может быть только в 3-й строке. Так как
его там нет, то данный ключ отсутствует в исходном множестве .
{7,13,6, 3, 9, 4, 8, 5}
h(k) = {1, 1, 0, 3, 3, 4, 2, 5}.
h(k)
0
1
2
3
4
5
Цепочки ключей
6
7,13
8
3, 9
4
5

13.

Поиск хешированием (пример 2)
Дано множество ключе
{7, 1, 8, 5, 14, 9, 16, 3, 4}.
Найти ключ K = 14. Хеш – функция равна h(k) = K mod
m;
m = [16/2] = 8 (т.к. 16 – максимальный ключ);
h(k) = {7, 1, 0, 5, 6, 1, 0, 3, 4}.
Для разрешения коллизий, которые присутствуют во множестве
хеш – функций построим таблицу:
При заполнении таблицы установим
соответствие между
исходным множеством и множеством хеш-функций. Поиск
осуществляется по таблице.
K = 14.
h(k) = 14 mod 8 = 6 это значит, что ключ K = 14 может быть
только в 6-й строке.
h(k)
0
1
3
4
5
6
7
Цепочки ключей
8,16
1,9
3
4
5
14
7