Правильные многогранники

1.

Апальков Я.В. 10а

2.

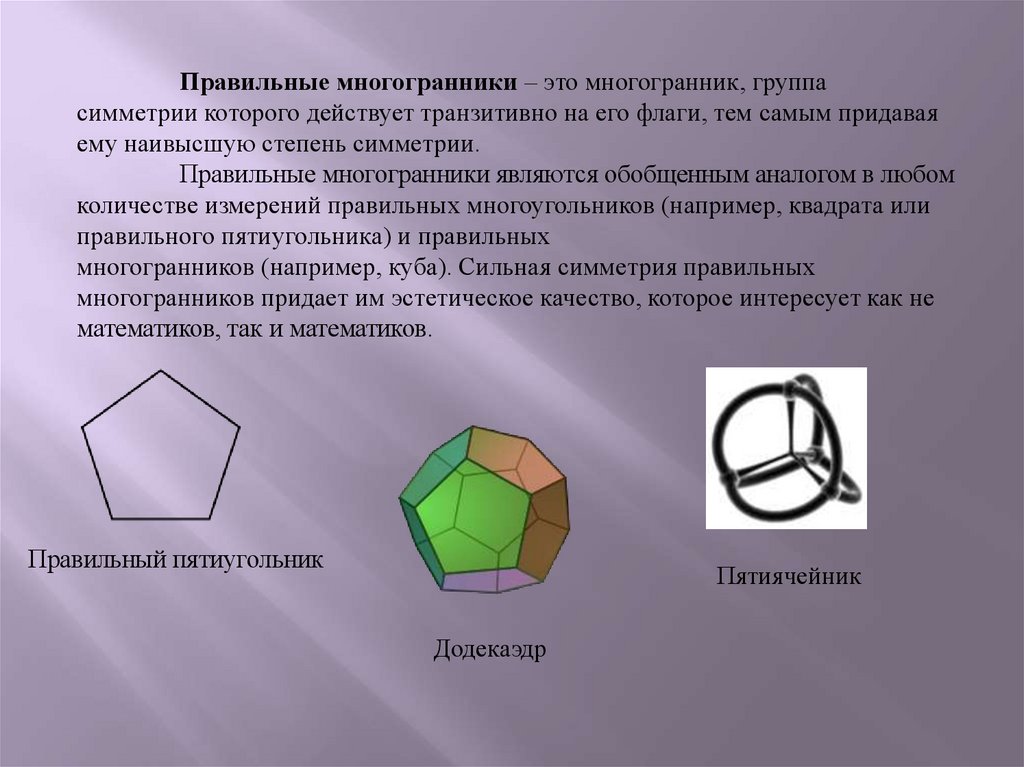
Правильные многогранники – это многогранник, группа
симметрии которого действует транзитивно на его флаги, тем самым придавая
ему наивысшую степень симметрии.
Правильные многогранники являются обобщенным аналогом в любом
количестве измерений правильных многоугольников (например, квадрата или
правильного пятиугольника) и правильных
многогранников (например, куба). Сильная симметрия правильных
многогранников придает им эстетическое качество, которое интересует как не
математиков, так и математиков.
Правильный пятиугольник
Пятиячейник
Додекаэдр

3.

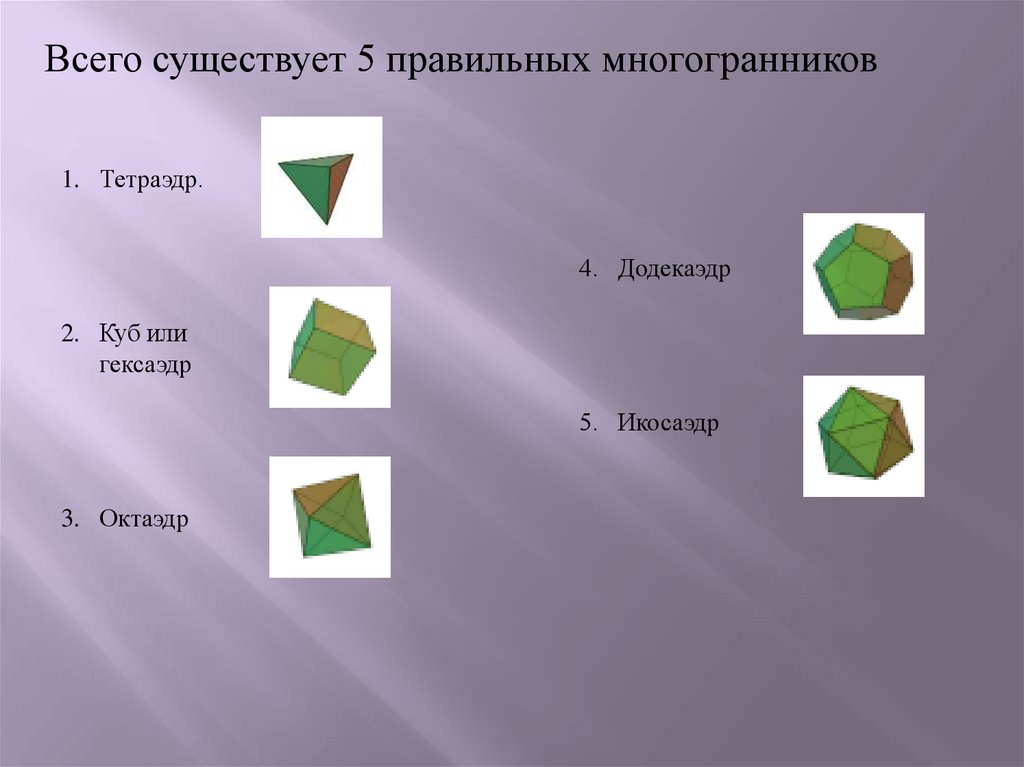
Всего существует 5 правильных многогранников
1. Тетраэдр.
4. Додекаэдр
2. Куб или
гексаэдр
5. Икосаэдр
3. Октаэдр

4.

Правильные многогранники известны с древнейших времён.
Их орнаментные модели можно найти на резных каменных
шарах, созданных в период позднего неолита, в Шотландии,
как минимум за 1000 лет до Платона. В костях, которыми люди
играли на заре цивилизации, уже угадываются формы
правильных многогранников.
В значительной мере правильные многогранники были
изучены древними греками. Некоторые источники (такие как Прокл Диадох)
приписывают честь их открытия Пифагору. Другие утверждают, что ему были
знакомы только тетраэдр, куб и додекаэдр, а честь открытия октаэдра и икосаэдра
принадлежит Теэтету Афинскому, современнику Платона. В любом случае, Теэтет
дал математическое описание всем пяти правильным многогранникам и первое
известное доказательство того, что их ровно пять.

5.

Правильные звёздчатые многогранники — это звёздчатые
многогранники, гранями которых являются одинаковые правильные
или звёздчатые многоугольники. В отличие от пяти
классических правильных многогранников, данные многогранники не
являются выпуклыми телами.
Полуправильные звёздчатые многогранники — это звёздчатые
многогранники, гранями которых являются правильные
или звёздчатые многоугольники, но не обязательно одинаковые. При
этом строение всех вершин должно быть одинаковым. Г. Коксетер, М.
Лонге-Хиггинс и Дж. Миллер в 1954 году перечислили 53 таких тела и
выдвинули гипотезу о полноте своего списка. Только значительно позже
в 1969 году Сопову С. П. удалось доказать, что представленный ими
список многогранников действительно полон.
Многие формы звёздчатых многогранников подсказывает сама природа.
Например, снежинки — это плоские проекции звёздчатых
многогранников. Некоторые молекулы имеют правильные структуры
объёмных фигур.

6.

Звёздчатые формы додекаэдра
Звёздчатая форма октаэдра
Звёздчатые формы икосаэдра

7.

Правильный n-мерный многогранник —
многогранник n-мерного евклидова
пространства, который являются наиболее
симметричными в некотором смысле.
Классификация правильных многомерных
многогранников была получена Людвигом
Шлефли.

8.

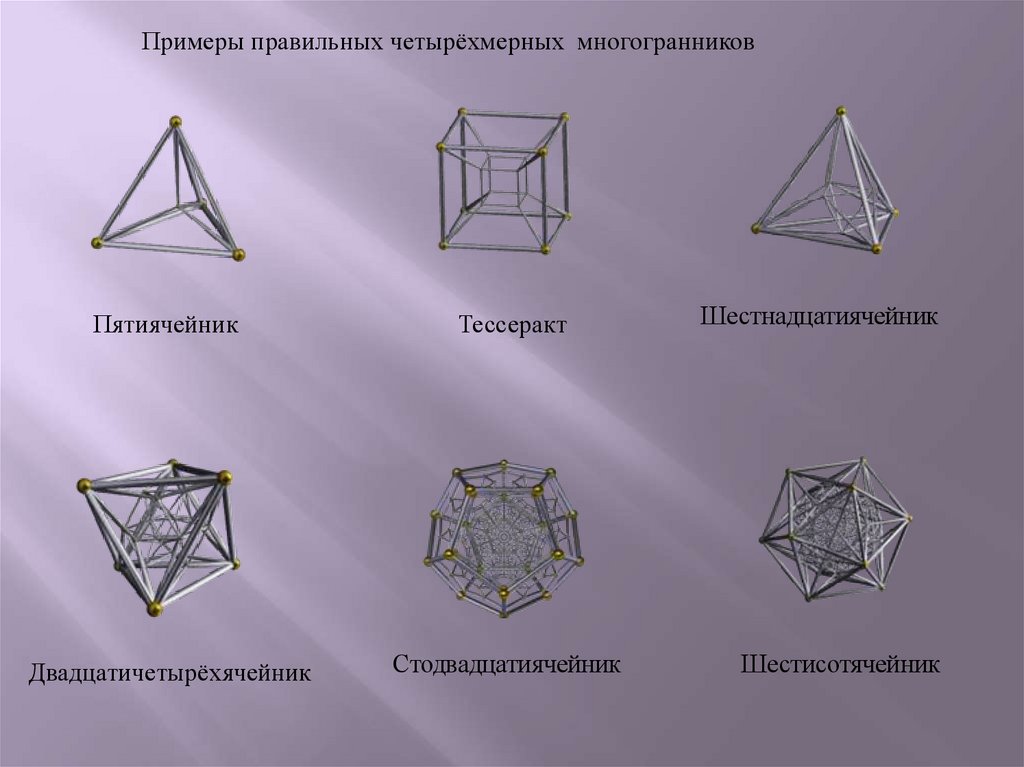
Пятиячейник. Состоит из 5 ячеек , где каждая ячейка
представляет собой тетраэдр.
Тессеракт. Состоит из 8 ячеек , где каждая ячейка
представляет собой куб.
Шестнадцатиячейник. Состоит из 16 ячеек , где каждая
ячейка представляет собой тетраэдр.
Двадцатичетырёхячейник. Состоит из 24 ячеек , где
каждая ячейка представляет собой октаэдр.
Стодвадцатиячейник. Состоит из 120 ячеек , где каждая
ячейка представляет собой додекаэдр.
Шестисотячейник. Состоит из 600 ячеек , где каждая
ячейка представляет собой октаэдр.

9.

Примеры правильных четырёхмерных многогранников
Пятиячейник
Тессеракт
Двадцатичетырёхячейник
Стодвадцатиячейник
Шестнадцатиячейник
Шестисотячейник

10.

1.
2.
3.
Начиная с пятимерного пространства
правильных многогранников или политопов
будет всего 3:
n-мерный правильный симплекс
n-мерный гиперкуб
n-мерный гипероктаэдр

11.

Символ Шлефли — комбинаторная характеристика правильного
многогранника, применяется для описания
правильных многогранников во всех размерностях. Назван в честь
швейцарского математика Людвига Шлефли, описавшего все
правильные многогранники в евклидовом пространстве
произвольной размерности.

12.

Символ Шлефли для правильного
многогранника Γ размерности записывается в
виде { p1, p2, p3,… pn−1}. Он индуктивно определяется следующим
образом:
Определим p1 как число сторон двумерной грани многогранника Γ.
Выберем одну из вершин P многогранника Γ и рассмотрим все вершины
Q1,…,Qk , соединённые с ней ребром. Заметим, что вершины Q1,…,Qk
лежат на гиперплоскости H, ортогональной прямой, соединяющей центр
многогранника с P. Сечение многогранника Γ с гиперплоскостью H
представляет собой правильный многогранник Γ′ размерности n−1.
Поскольку все вершины Γ равноправны, тип этого многогранника не
зависит от выбора вершины P. Определим p2 как число сторон двумерной
грани многогранника Γ′.
Продолжая действовать таким образом до тех пор, пока получающееся
сечение имеет двумерную грань, мы получим символ Шлефли
многогранника Γ.
Заметим, что символ Шлефли n-мерного многогранника состоит из
n−1 целого числа, каждое из которых не меньше 3.