Касательная к окружности. Окружность, вписанная в угол

1.

Касательная к окружности.
Окружность, вписанная в угол.

2.

Взаимное расположение прямой и окружности
В плоскости прямая и окружность могут пересекаться или не пересекаться.
При пересечении могут иметь одну или две общие точки.
1. Если расстояние от центра окружности до прямой больше радиуса, то у
прямой и окружности общих точек нет.

3.

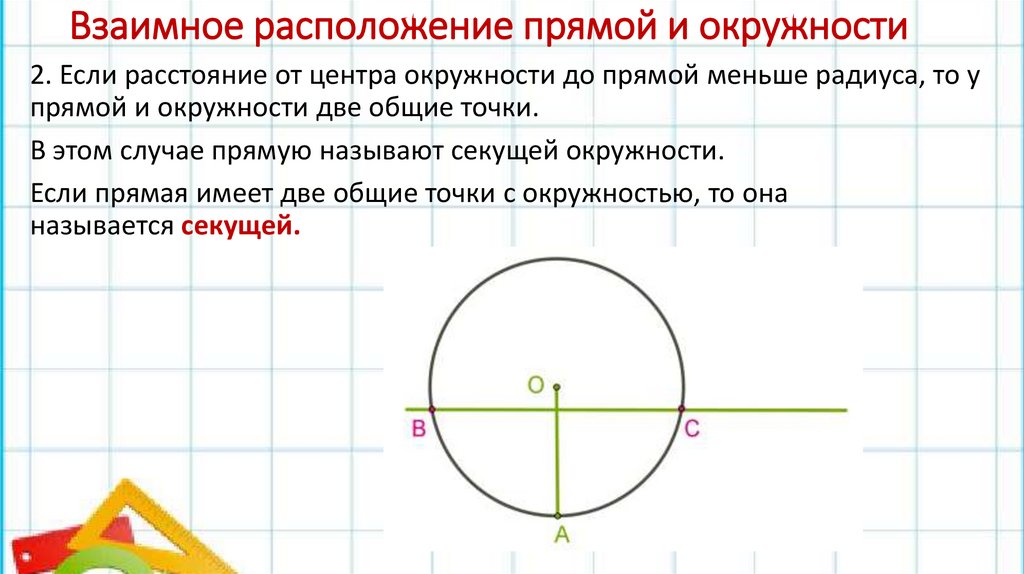
Взаимное расположение прямой и окружности
2. Если расстояние от центра окружности до прямой меньше радиуса, то у
прямой и окружности две общие точки.
В этом случае прямую называют секущей окружности.
Если прямая имеет две общие точки с окружностью, то она
называется секущей.

4.

Взаимное расположение прямой и окружности
3. Если расстояние от центра окружности до прямой равно радиусу, то у
прямой и окружности одна общая точка.
В этом случая прямую называют касательной к окружности.
Касательной к окружности называется прямая, имеющая с окружностью
одну общую точку.

5.

Теорема
Касательная к окружности перпендикулярна радиусу, проведённому в
точку касания.
Доказательство
Предположим, что радиус OA не перпендикулярен к прямой, но является наклонной.
Тогда из точки O можно провести перпендикуляр к прямой, который будет короче
радиуса. А это означает, что расстояние от центра окружности до прямой меньше
радиуса, и у прямой и окружности должны быть две общие точки. Но это
противоречит данной информации, наше предположение неверно.

6.

Теорема
Центр вписанной в угол окружности лежит на
его биссектрисе.
Доказательство
Пусть О – центр некоторой окружности,
вписанной в ВАС. Пусть В – точка касания
окружности и касательной АВ, С – точка касания
окружности и касательной АС. ОВ и ОС –
радиусы, проведенные в точки касания. Значит,
ОВ АВ, ОС АС. Тогда АВО и АСО –
прямоугольные. Они равны по общей гипотенузе
АО и равным катетам ВО и СО – радиусы. Из
равенства треугольников следует, что ВАО =
САО, а АО – биссектриса.

7.

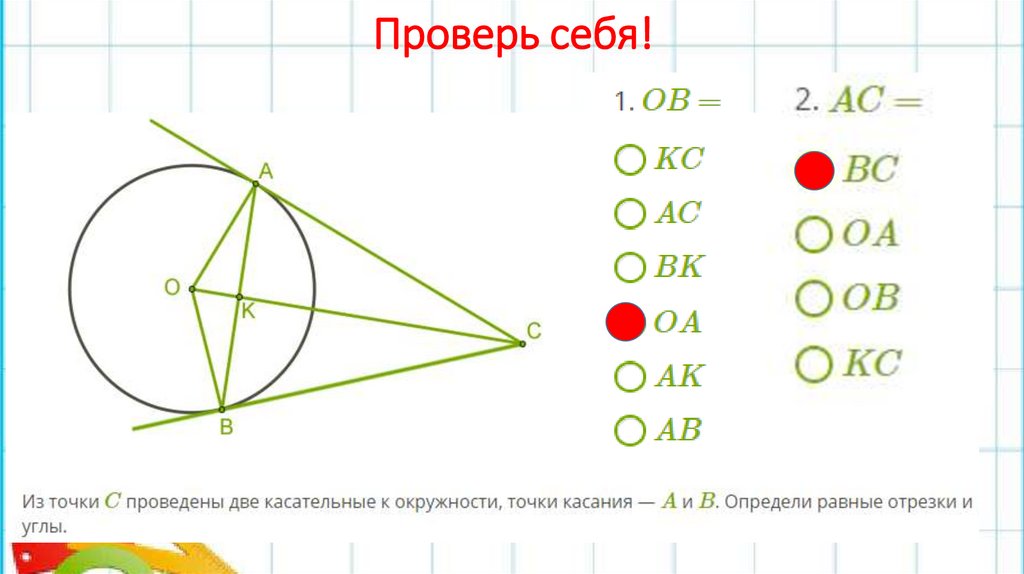
Теорема
Отрезки касательных к окружности, проведенных
из одной точки, равны и составляют равные углы
с прямой, проходящей через эту точку и центр
окружности.
Дано: АС и АВ – касательные
Доказать: АС = АВ, САО = ВАО
Доказательство
1. Так как АС и АВ – касательные, то АС ОС,
АВ ОВ, а АСО и АВО – прямоугольные.
2. АСО = АВО (по общей гипотенузе АО, и
равным катетам ОС = ОВ – радиусы).
3. Из равенства треугольников следует, что
АС = АВ, САО = ВАО

8.

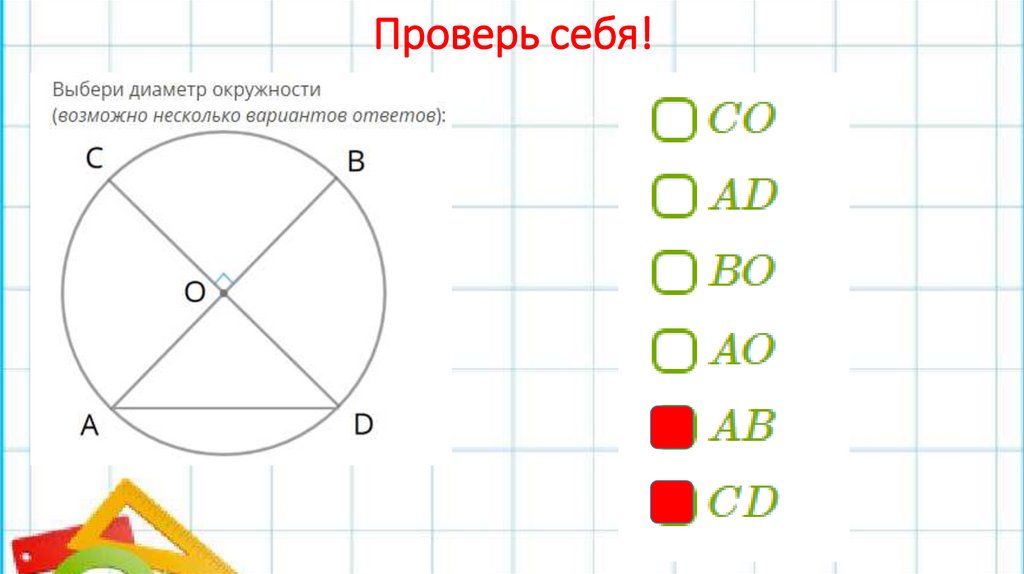
Проверь себя!

9.

Проверь себя!

10.

Проверь себя!

11.

Проверь себя!

12.

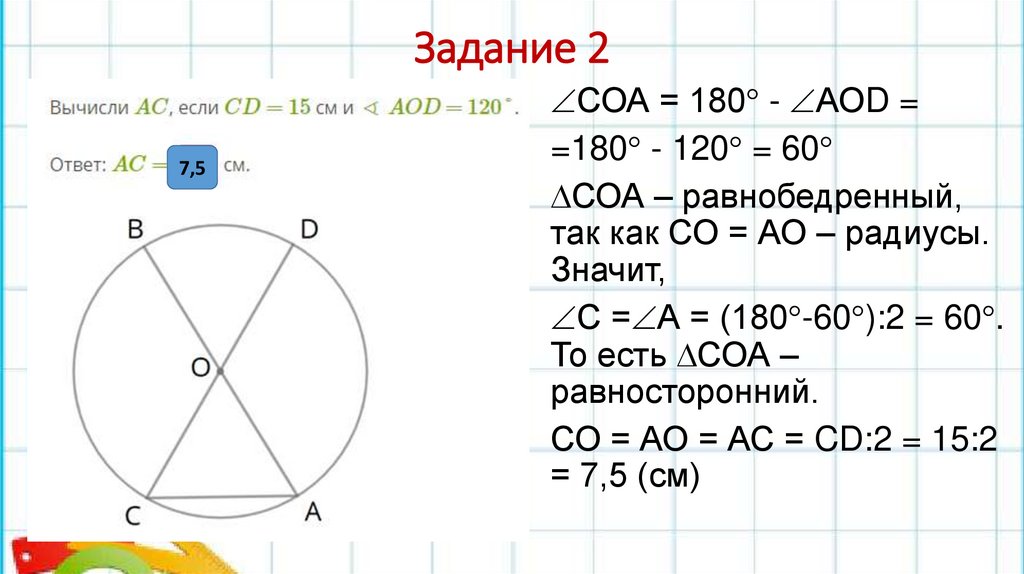
Задание 2
7,5
СОА = 180 - АОD =
=180 - 120 = 60
СОА – равнобедренный,
так как СО = АО – радиусы.
Значит,
С = А = (180 -60 ):2 = 60 .
То есть СОА –
равносторонний.
СО = АО = АС = CD:2 = 15:2
= 7,5 (см)

13.

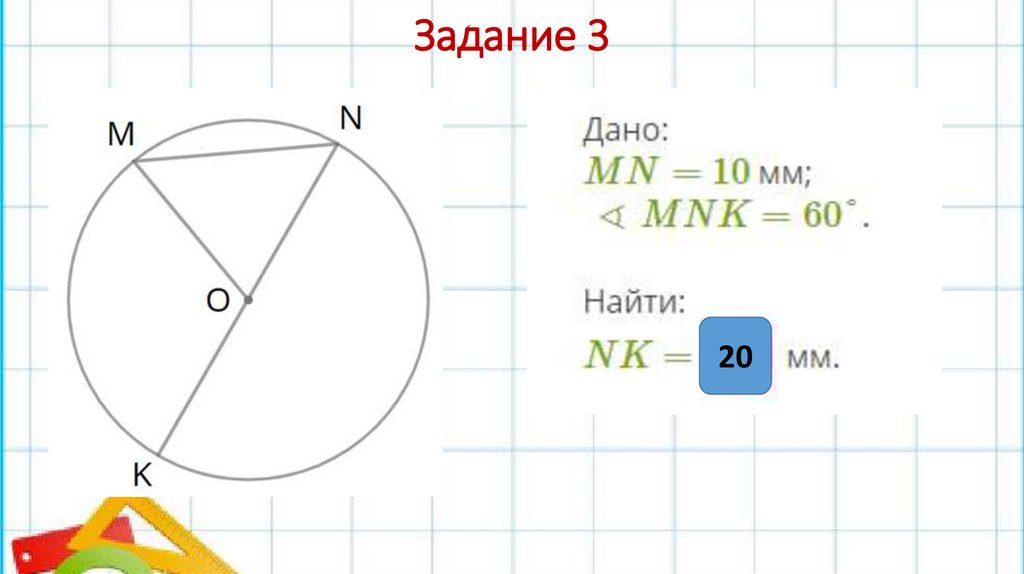
Задание 3
20

14.

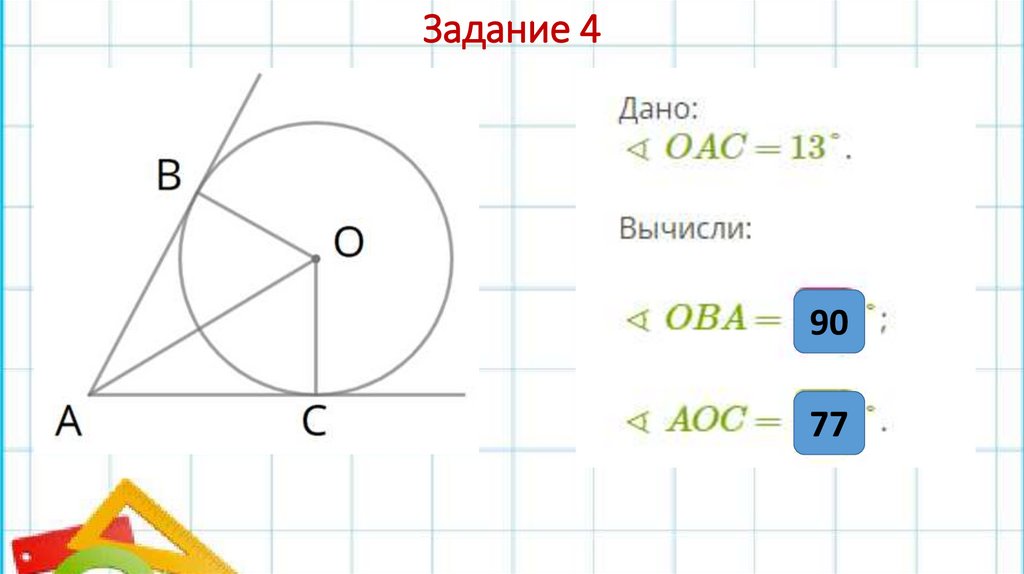
Задание 4
90
77

15.

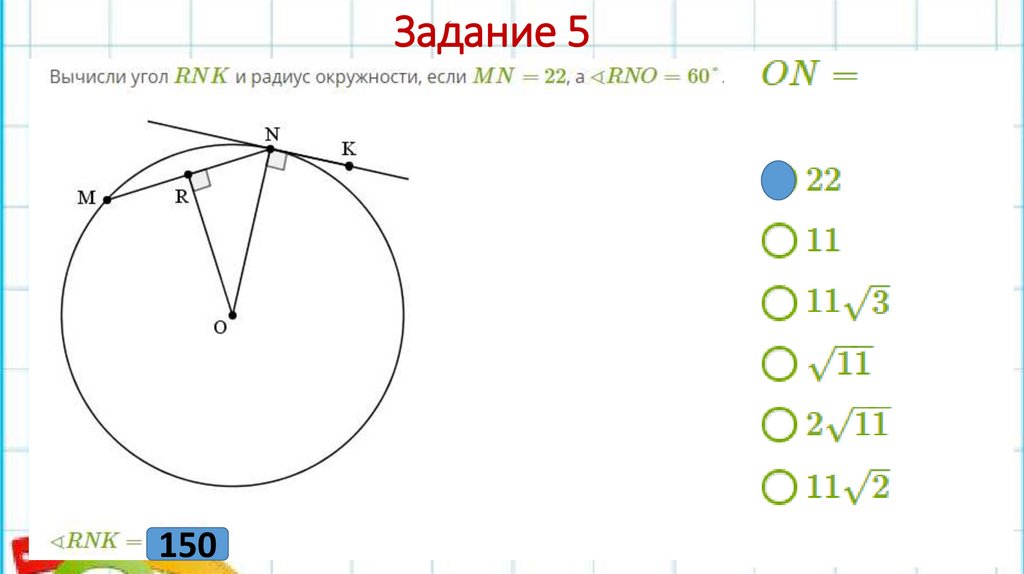
Задание 5
150

16.

Задание 6
34

17.

Задание 7
63

18.

Домашнее задание:
Выучить правила § 1, п.70, 71
Выполнить в тетради: № 631, 640

19.

Успешного выполнения домашнего задания!

20.

Использованные источники:
• https://foxford.ru/wiki/matematika/kasatelnaya-k-okruzhnosti
• https://skysmart.ru/articles/mathematic/kasatelnaya-k-okruzhnosti
• https://www.yaklass.ru/p/geometria/8-klass/okruzhnost9230/kasatelnaia-i-okruzhnost-9242/re-ca89ade5-1388-4df8-af6dbe4437358f63

21.

Скачано с www.znanio.ru