Similar presentations:
Нечеткая логика в системах управления
1.
Нечеткая логика в системахуправления
2.
ОпределениеНечёткая логика (англ. fuzzy logic) — раздел математики,
являющийся обобщением классической логики и теории
множеств, базирующийся на понятии нечёткого множества.
Задачей нечеткой логики является рассмотрение объекта с
функцией принадлежности элемента ко множеству, принимающей
любые значения в интервале [0,1], а не только 0 или 1, как в
Булевой алгебре. На основе этого понятия вводятся различные
логические операции над нечёткими множествами и
формулируется понятие лингвистической переменной, в качестве
значений которой выступают нечёткие множества.
Предметом нечёткой логики считается исследование
рассуждений в условиях нечёткости, размытости, сходных с
рассуждениями в обычном смысле, и их применение в
вычислительных системах.
3.
Нечеткаялогика
основана на использовании
таких оборотов естественного
языка, как «далеко», «близко»,
«холодно», «горячо». Диапазон
ее применения очень широк от бытовых приборов до
управления
сложными
промышленными процессами.
Многие современные задачи
управления просто не могут
быть решены классическими
методами из-за очень большой
сложности
математических
моделей, их описывающих.
4.
Принцип работы НЛВ теории множеств элемент либо принадлежит множеству,
либо нет. Понятия множеств используется во многих
математических теориях. Это важное понятие, однако, не
рассматривает простые ситуации, когда не все ясно и понятно.
Например при выборе фруктов очень не сложно определить
общий набор яблок, при этом непросто определить набор спелых
яблок. Учитывая, что яблоки созревают постепенно, понятие
набора спелых яблок, таким образом, является нечетким
(расплывчатым).
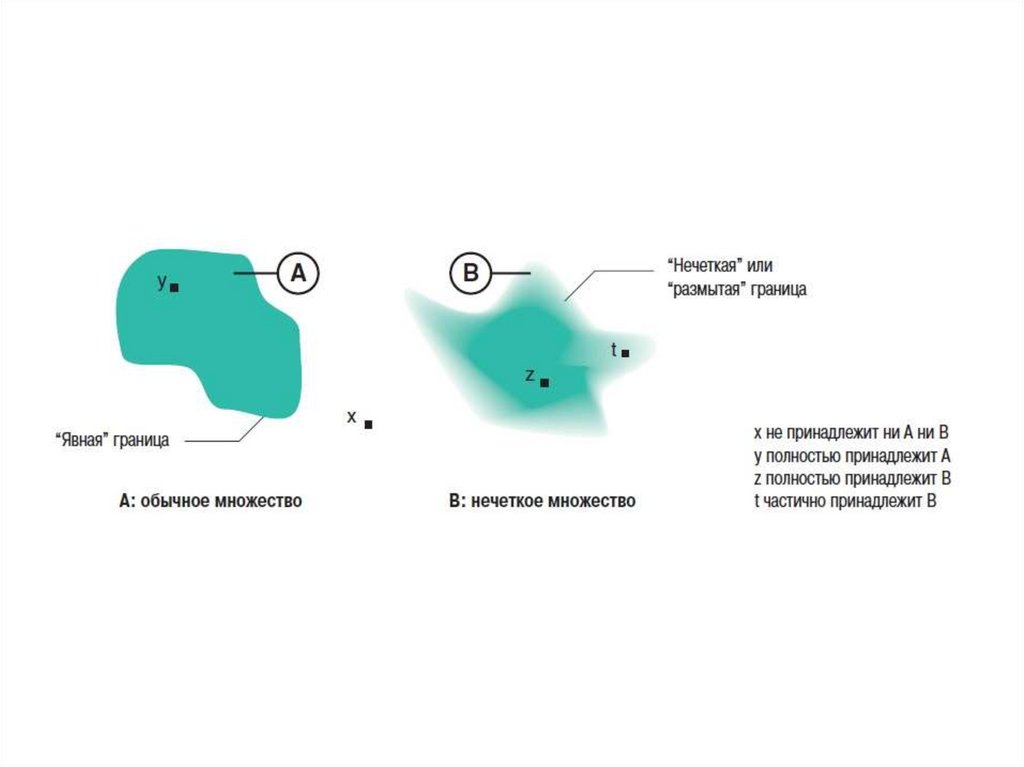
Понятие нечеткого множества было принято для того,
чтобы учесть расплывчатость решения задачи. Теория нечетких
множеств базируется на понятии частичной принадлежности к
множеству: каждый элемент принадлежит к нечеткому множеству
немного или частично. Очертание нечеткого множества не имеет
“Явной” границы, а представляется “нечетким” или “размытым”.
5.
6.
7.
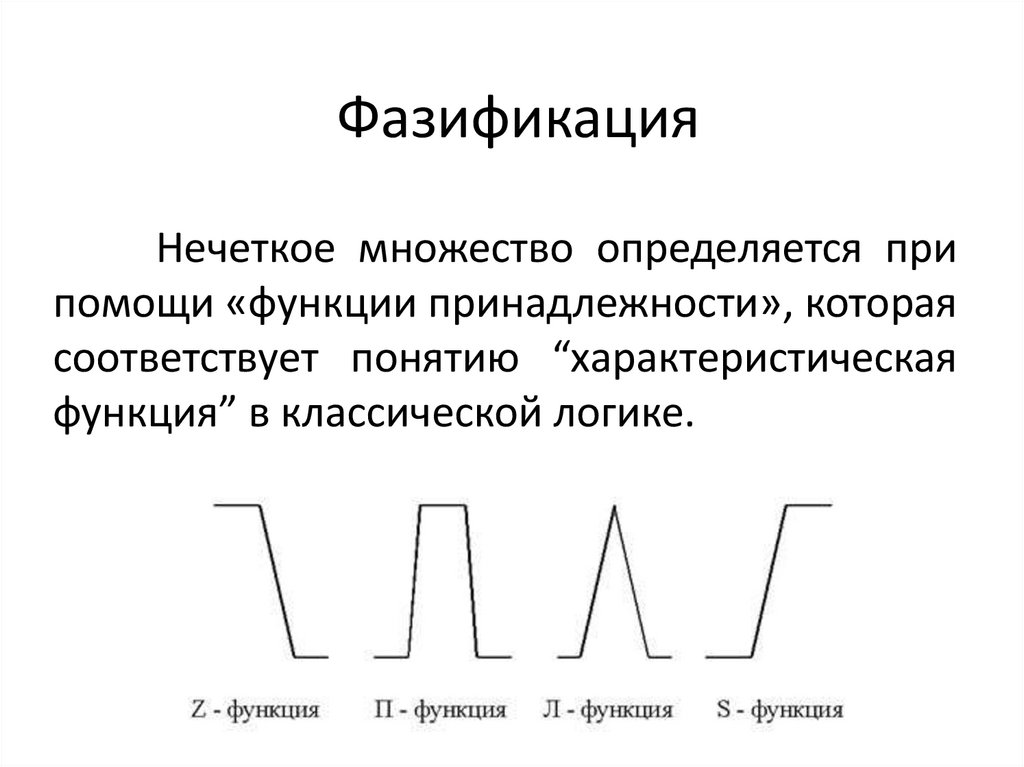
ФазификацияНечеткое множество определяется при
помощи «функции принадлежности», которая
соответствует понятию “характеристическая
функция” в классической логике.
8.
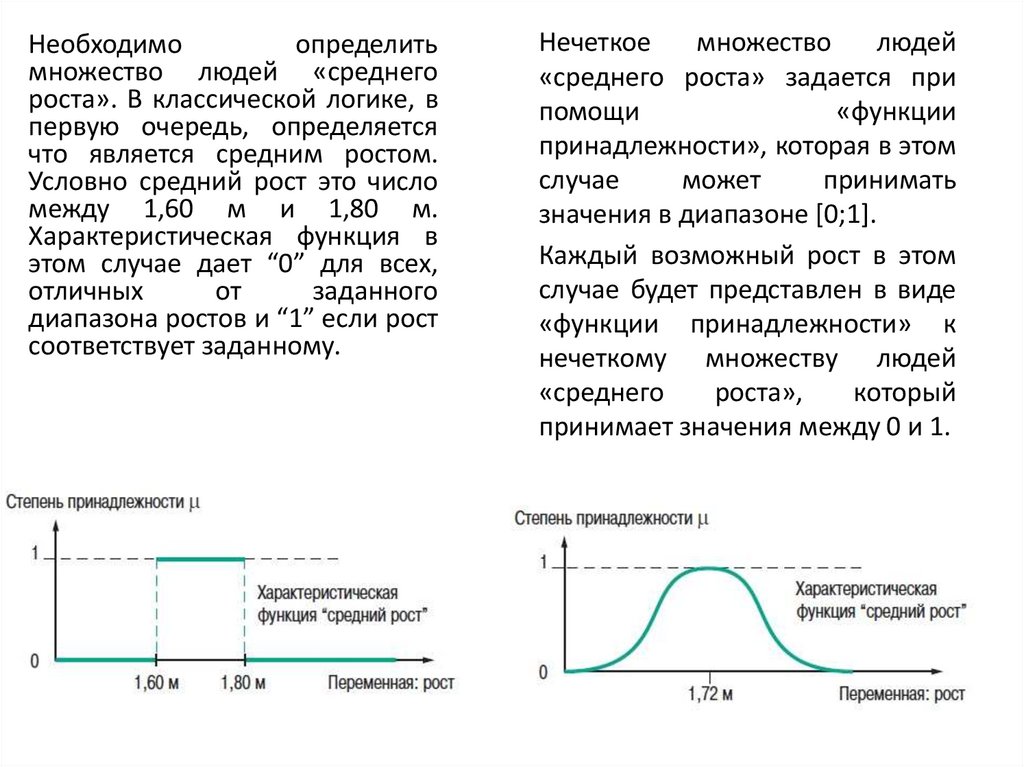
Необходимоопределить
множество людей «среднего
роста». В классической логике, в
первую очередь, определяется
что является средним ростом.
Условно средний рост это число
между 1,60 м и 1,80 м.
Характеристическая функция в
этом случае дает “0” для всех,
отличных
от
заданного
диапазона ростов и “1” если рост
соответствует заданному.
Нечеткое
множество
людей
«среднего роста» задается при
помощи
«функции
принадлежности», которая в этом
случае
может
принимать
значения в диапазоне [0;1].
Каждый возможный рост в этом
случае будет представлен в виде
«функции принадлежности» к
нечеткому множеству людей
«среднего
роста»,
который
принимает значения между 0 и 1.
9.
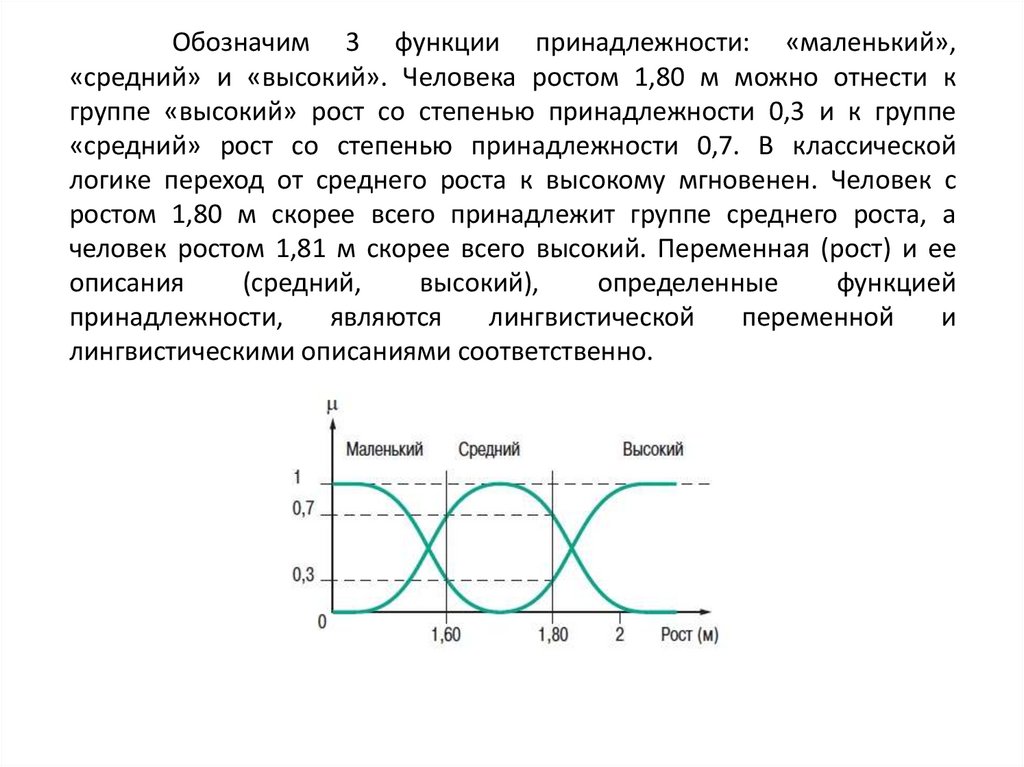
Обозначим 3 функции принадлежности: «маленький»,«средний» и «высокий». Человека ростом 1,80 м можно отнести к
группе «высокий» рост со степенью принадлежности 0,3 и к группе
«средний» рост со степенью принадлежности 0,7. В классической
логике переход от среднего роста к высокому мгновенен. Человек с
ростом 1,80 м скорее всего принадлежит группе среднего роста, а
человек ростом 1,81 м скорее всего высокий. Переменная (рост) и ее
описания
(средний,
высокий),
определенные
функцией
принадлежности,
являются
лингвистической
переменной
и
лингвистическими описаниями соответственно.
10.
Формирование правилДля построения правил используются операторы AND, OR и NOT и таким
образом правило имеет вид:
IF «Разумная цена аренды» AND
«Достаточная площадь» THEN «Подходящая квартира»
Логическим оператором пересечения множеств является оператор AND.
Степенью истинности предположения «A AND B» является минимум из
степеней истинности A и B:
μ(A AND B) = MIN(μ(A),μ(B))
Например:
«Низкая Температура» истинно на 0,7.
«Низкое Давление» истинно на 0,5.
Поэтому утверждение «Низкая Температура» AND «Низкое Давление»
истинно на 0,5 = MIN(0,7; 0,5).
ВАЖНО: при использовании AND в нечеткой логике результат аналогичен
классической логике: 0 и 1 получается 0.
11.
Логическим оператором объединения множеств является оператор OR.Степенью истинности предположения «A OR B» является максимум из
степеней истинности предположений A и B:
μ(A OR B) = MAX(μ(A),μ(B))
Например:
«Низкая Температура» истинно на 0,7.
«Низкое Давление» истинно на 0,5.
Поэтому утверждение «Низкая Температура» OR «Низкое Давление» истинно
на 0,7.
ВАЖНО: при использовании OR в нечеткой логике результат аналогичен
классической логике: 0 OR 1 получается 1.
Логический оператор отрицания обозначается NOT.
μ(NOT A) = 1 - μ(A)
Например:
«Низкая Температура» истинно на 0,7.
Поэтому утверждение NOT «Низкая Температура» (можно записать как
«Температура НЕ низкая») истинно на 0,3.
ВАЖНО: при использовании NOT в нечеткой логике результат аналогичен
классической логике NOT(0) получается 1 и NOT(1) получается 0.
12.
Пример описания системы управления климатом:горячий, влажный воздух не комфортен (формируется испарина);
аналогично дыхание затруднено, если воздух холодный и очень сухой.
Наиболее комфортная ситуация, когда воздух горячий и сухой или
холодный и влажный. Эти формулы могут быть описаны на языке
нечеткой логики:
Комфорт = (Низкая температура AND Высокая влажность) OR (Высокая
температура AND Низкая влажность).
Это логическое выражение описывает ощущение человека в
помещении, в котором отсутствует принудительная циркуляция
воздуха.
13.
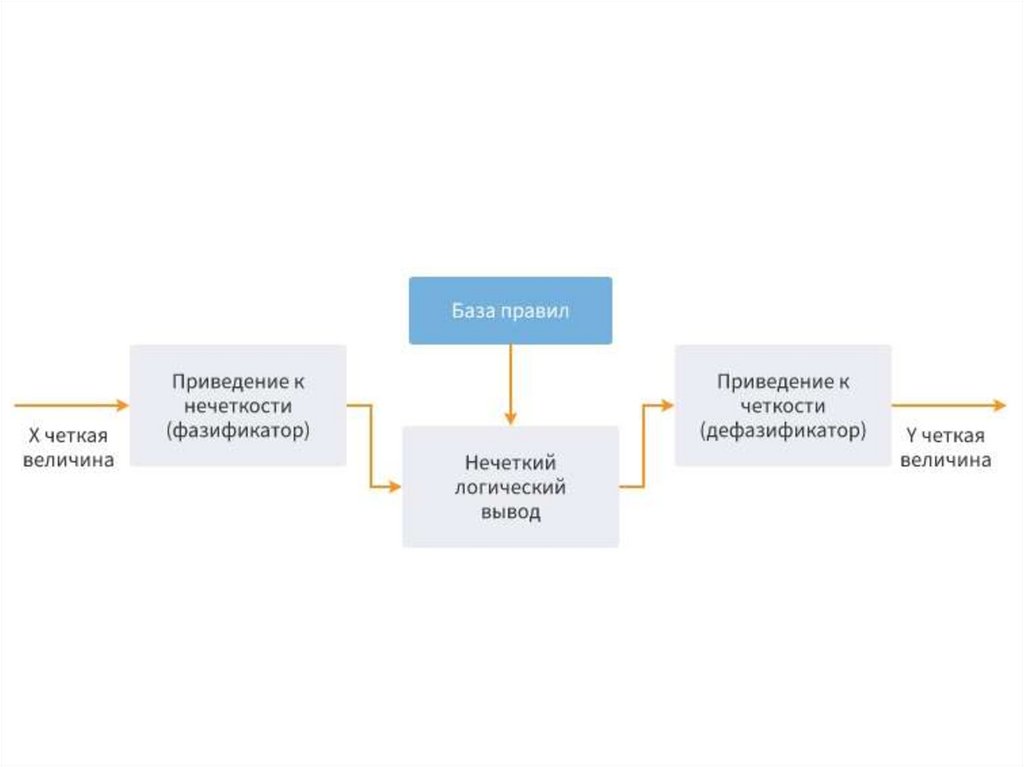
Нечеткий логический выводНаиболее
часто
используется
механизм
нечеткого
логического
вывода,
называемый
механизмом Мамдани. Он представляет собой
упрощение более общего механизма, который
базируется на “нечетком выводе” и обобщенном
правиле дедукции.
Основная идея:
База нечетких правил Мамдани содержит
лингвистические правила, использующие функции
принадлежности
для
описания
применяемых
концепций.
14.
15.
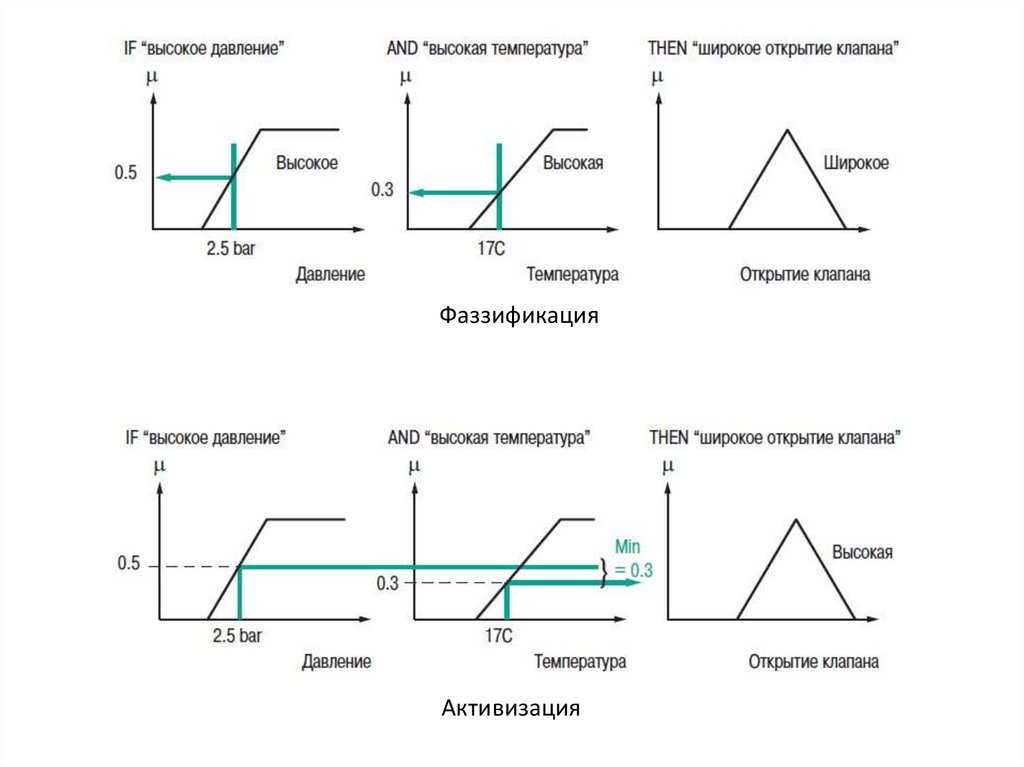
ФаззификацияАктивизация
16.
РезультатСтепень активизации правила используется для
того, чтобы определить результат правила: данная
операция
называется
выводом
результата.
Применяются
несколько
операторов
вывода
результата, чаще всего используется оператор выбора
минимума.
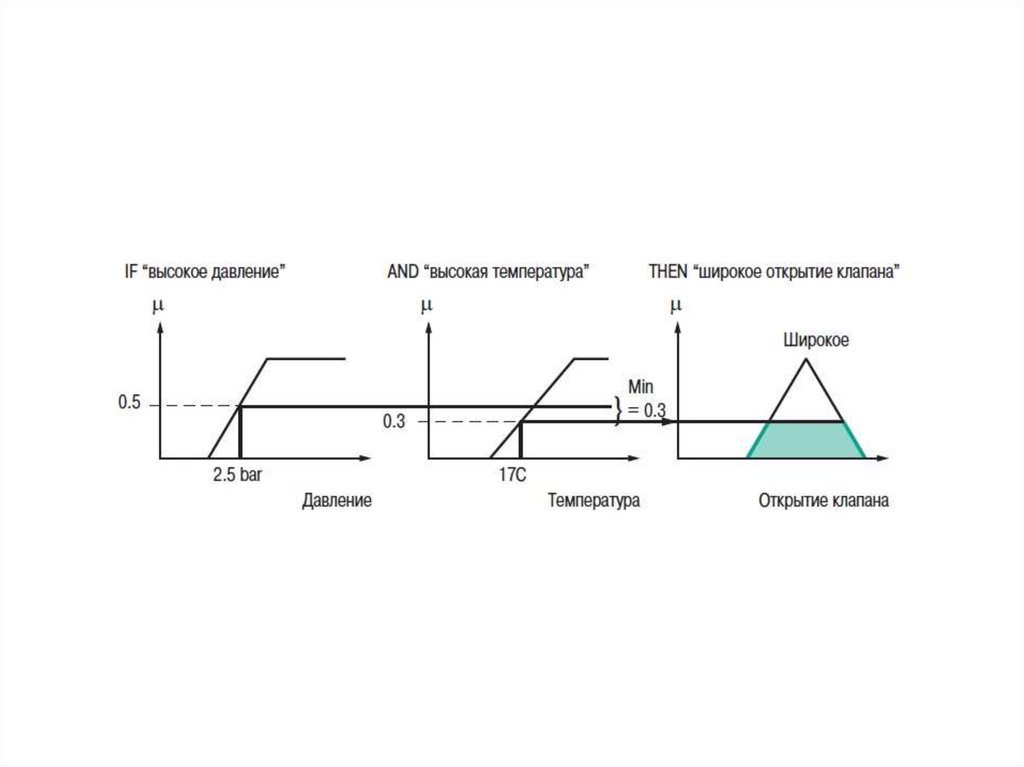
Результирующее нечеткое множество строится с
помощью поиска минимальных значений среди
степеней активизации и функций принадлежности и
сортировки «урезанных» функций принадлежности
17.
18.
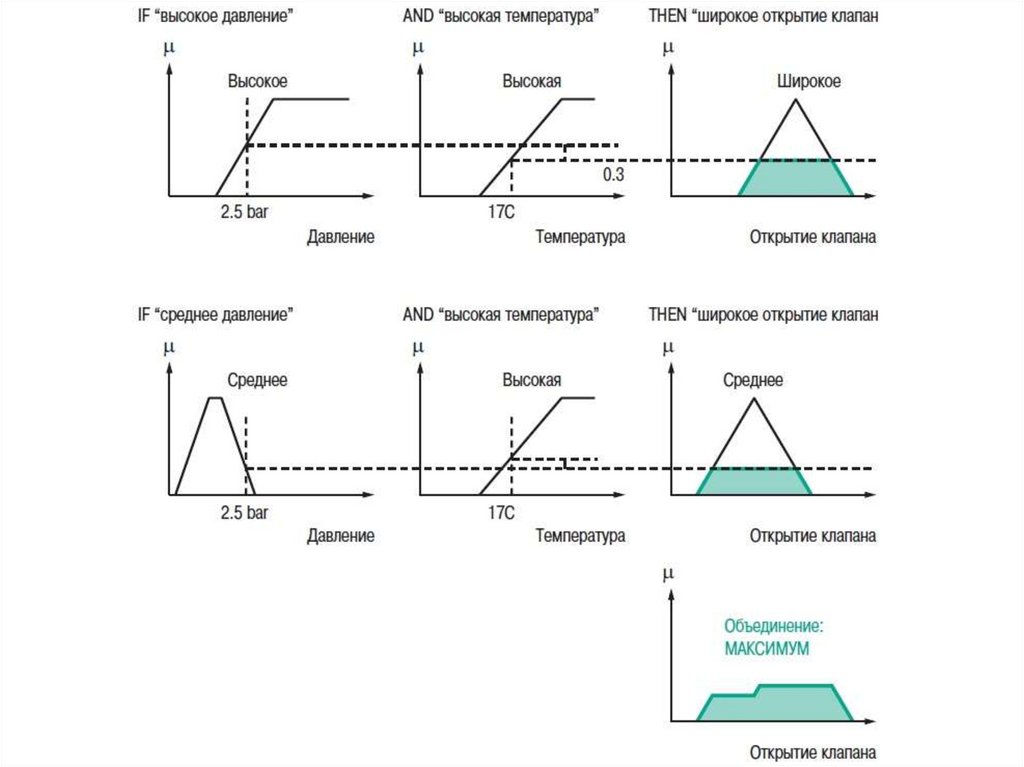
ОбъединениеОбщее выходное нечеткое множество получается
путем
объединения
нечетких
множеств,
полученных в результате применения каждого
правила формирования для данного выхода. На
примере ниже представлен случай, когда на
формирование одного выхода влияют два правила.
Предполагается, что правила связаны логической
операцией “OR”, поэтому необходимо найти
максимальное значение среди результирующих
функций принадлежности для каждого правила
19.
20.
ДефазификацияНа последнем этапе нечеткого логического
вывода,
выходное
нечеткое
множество
уже
определено, но оно не может быть напрямую
использовано для предоставления оператору точной
информации или для управления исполнительным
механизмом. Необходимо выполнить переход из
“мира нечеткой логики” в “реальный мир”.
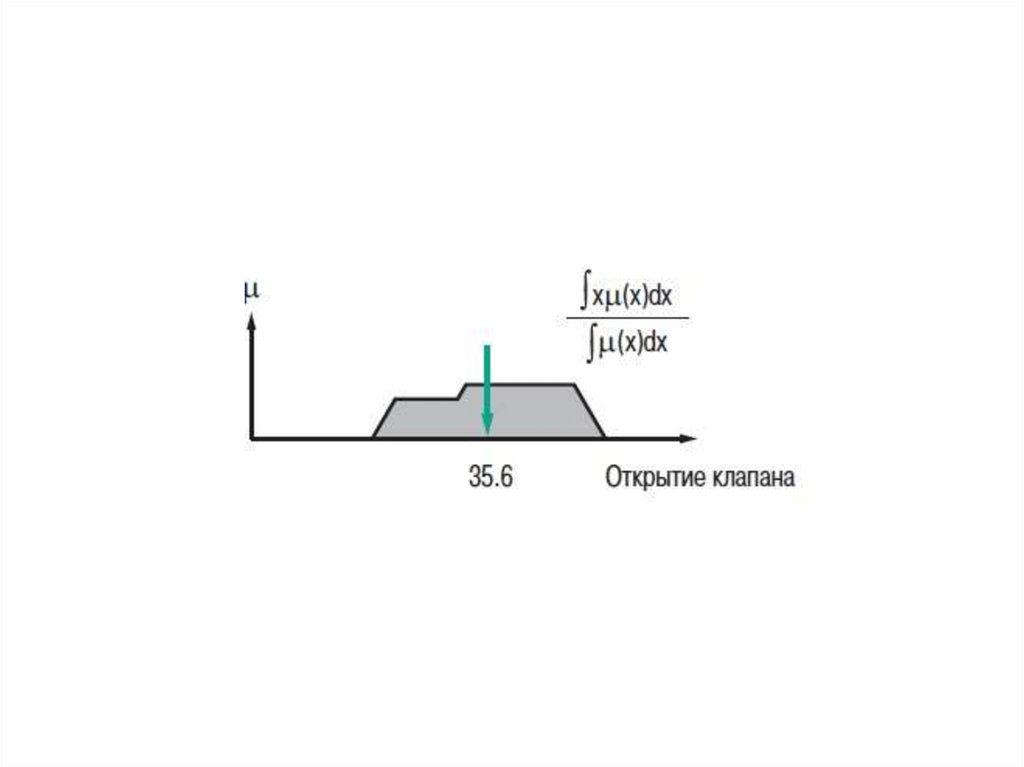
Можно использовать разнообразные методы
дефазификации, однако чаще всего используется
метод вычисления “центра тяжести” нечеткого
множества
21.
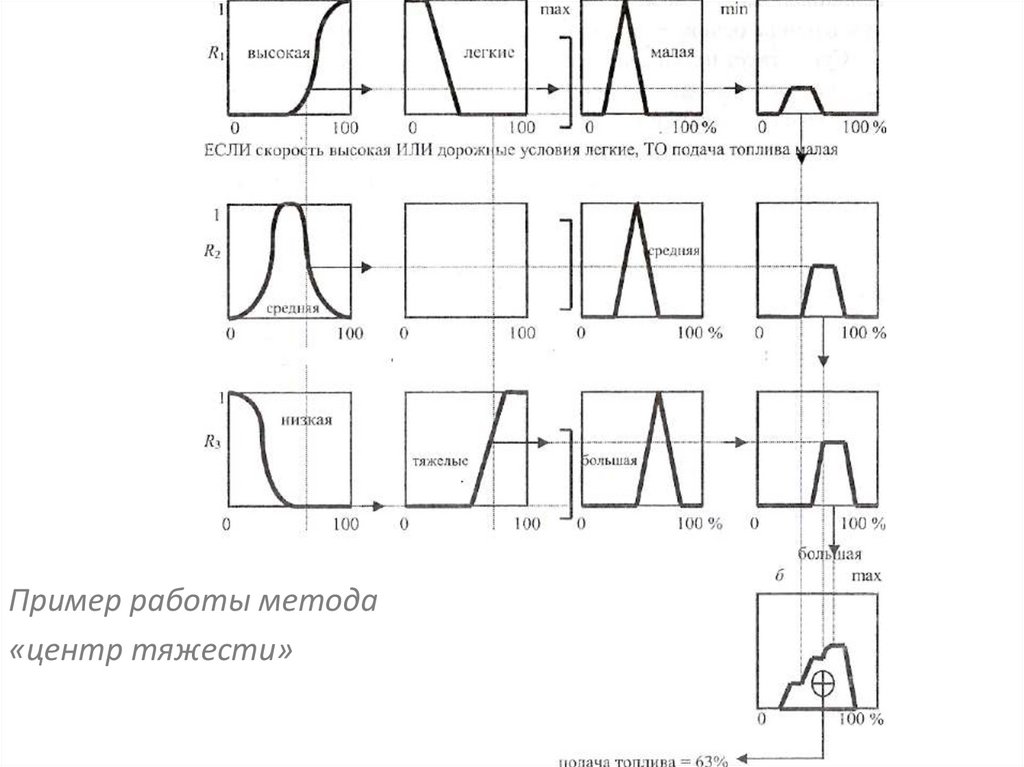
22.
Пример работы метода«центр тяжести»
23.
Математический аппарат, используемый в традиционныхметодах автоматического управления, не всегда в полной мере
может удовлетворить нуждам современного производства.
Поэтому в последнее время находят широкое распространение
так называемые “мягкие вычисления”, основной принцип
которых заключается в обеспечении приемлемого качества
управления в условиях неопределённости при относительно
невысоком уровне затрачиваемых ресурсов (стоимостных,
временных, вычислительных и т.п.). К мягким вычислениям в
настоящее время относят такие информационные технологии,
как экспертные системы, нейронные сети, нечеткие системы,
генетические алгоритмы и ряд других. Говоря простым языком,
мягкие вычисления – вычисления, относящиеся к классу
неточных решений, основанных на приближенных методах
решения задач
24.
В настоящее время, несмотря на довольно высокийуровень автоматизации технологических процессов на
нефтеперерабатывающих заводах или тепловых электрических
станциях, существует ряд процессов, где влияние человеческого
фактора является определяющим из-за технологических
особенностей объекта и сложностей, возникающих при
применении классических методов теории управления.
Как следствие, невозможно избежать влияния
ошибочных действий оператора, что может приводить к
повышенному риску возникновения аварийных режимов.
25.
С другой стороны, качество управления в значительнойстепени определяется опытом оператора по эксплуатации
объекта, в частности, в некоторых ситуациях отчасти
интуитивные решения, принятые оператором в нетривиальных
ситуациях, оказываются наиболее верными. Таким образом, при
решении задачи автоматического управления (например
подпиткой теплосети) необходимо основываться как на
технологических требованиях, предъявляемых к процессам
химической очистки воды и режимам работы, так и на опыте
операторов, эксплуатирующих объект в течение длительного
срока и обладающих необходимыми знаниями о возможных
неопределенностях, возникающих в процессе работы объекта.
26.
Установка, осуществляющая процесс химической очисткиводы для подпитки теплосети состоит из нескольких
Н-катионитных фильтров, предназначенных для умягчения
воды. При истощении фильтра проводят его регенерацию. В
процессе работы фильтра и перед его регенерацией проводят
взрыхление водой. Цель взрыхления заключается в устранении
уплотненностей
катионитного
слоя
для
снижения
гидравлического сопротивления фильтра и обеспечения
свободного доступа воды и регенерационного раствора к
зернам катионита.
27.
Нагрузка на блок, состоящий из 6 фильтров определяетсятекущим расходом воды. Поэтому, в зависимости от требуемой
производительности блока, число одновременно работающих
фильтров определяется требованием их номинальной нагрузки.
Решение по переключению фильтра из одного состояния
в другое в настоящий момент принимается оператором, то есть
управление распределением нагрузки на блок фильтров ведется
в ручном режиме, что снижает оперативность и точность
принятия решений.
28.
Задачейавтоматического
управления
является
определение момента переключения фильтра в одно из
возможных состояний (работа, резерв, взрыхление) таким
образом, чтобы достигался заданный расход воды на блок и
соблюдался требуемый режим на каждом конкретном фильтре
блока,
другими
словами
должна
решаться
задача
распределения нагрузки между фильтрами блока, совместно с
задачей стабилизации общего расхода воды на блок.
Поставленная задача является нетривиальной из-за
сложности объекта регулирования. При её решении
применение классического подхода затруднительно из-за
больших сложностей возникающих при идентификации
объекта, описании его математической модели и отсутствия
четких правил переключения фильтров.
29.
Оператор, в ситуации такой неопределенности, исходя изтекущего состояния объекта и опыта эксплуатации, по существу,
интуитивно принимает решения по управлению их работой.
Поэтому целесообразно применить к решению поставленной
задачи методы интеллектуального управления как инструмента
позволяющего качественно использовать знания об объекте в
форме логиколингвистических изъяснений и задействовать весь
накопленный опыт эксплуатации объекта при разработке
алгоритма
принятия
решения.
Из
всех
систем
интеллектуального управления наиболее подходящими к
решению поставленной задачи являются системы основанные
на использовании нечеткой логики.
30.
Адаптивные нечеткие системыКлассические нечеткие системы обладают тем
недостатком, что для формулирования правил и функций
принадлежности необходимо привлекать экспертов той или
иной предметной области, что не всегда удается обеспечить.
Адаптивные нечеткие системы (adaptive fuzzy systems) решают
эту проблему. В таких системах подбор параметров нечеткой
системы
производится
в
процессе
обучения
на
экспериментальных данных.
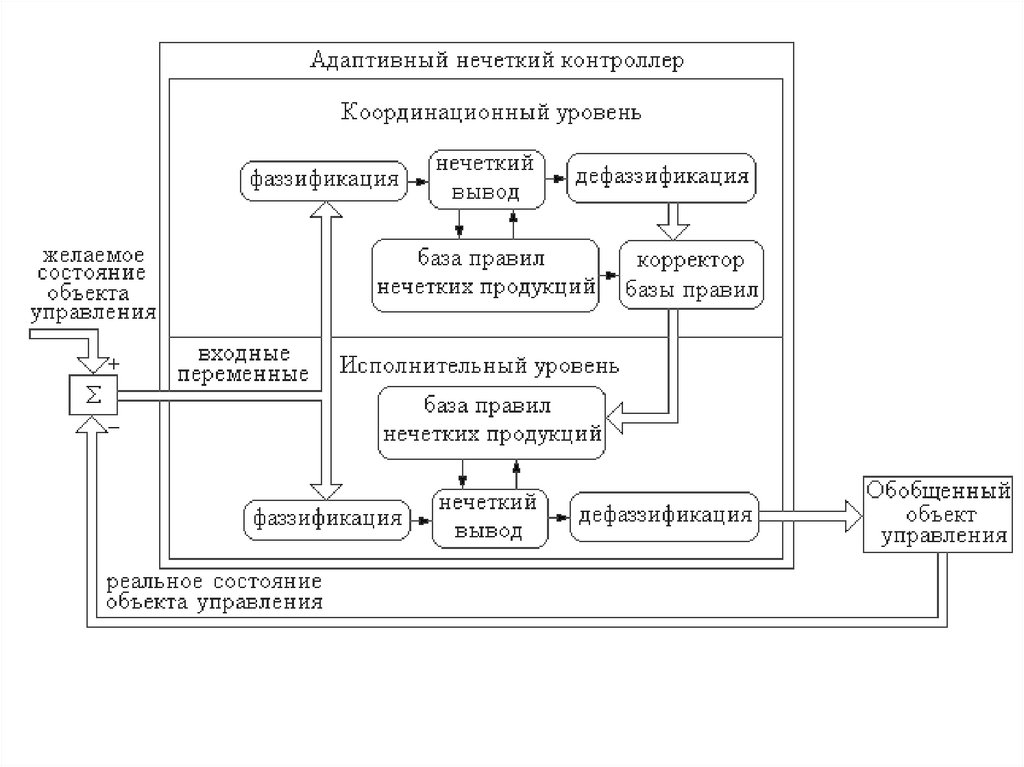
31.
Адаптивнаянечеткая
САУ
представляет
собой
двухуровневую систему с нечетким контроллером на ведомом
исполнительном уровне и нечетким блоком адаптации на
ведущем координационном уровне.
Принцип работы адаптивного нечеткого контроллера,
объединяющего в своем составе координационный и
исполнительный уровни управления, заключается в следующем.
При существенном изменении поведения объекта в текущей
ситуации, характеризующейся различиями между реальным и
желаемы состоянием объекта управления, система нечеткого
вывода контроллера исполнительного уровня продуцирует
управление, реализация которого уже не обеспечивает
необходимого качества регулирования.
32.
В этом случае блок адаптации координационного уровня,пользуясь собственной системой нечеткого вывода, производит
коррекцию продукционных правил нечеткого контроллера
исполнительного уровня. Непосредственное изменение базы
правил нечеткого контроллера исполнительного уровня
осуществляет корректор базы правил. Как правило,
лингвистической коррекции подвергаются те продукционные
правила, активизация которых привела к неадекватному
управлению, с точки зрения лингвистической оценки
управления, содержащейся в базе знаний координационного
уровня.
Таким образом, на координационном уровне происходит
нечеткая оценка управления и, при необходимости, коррекция
базы продукционных правил нечеткого контроллера, т.е.
фактически производится интеллектуальная оценка и коррекция
поведения системы управления, которое определяется в виде
нечетких продукций на исполнительном уровне
33.
34.
Алгоритмы обучения адаптивных нечетких системотносительно трудоемки и сложны по сравнению с алгоритмами
обучения нейронных сетей, и, как правило, состоят из двух
стадий:
- генерация лингвистических правил;
- корректировка функций принадлежности.
Первая задача относится к задаче переборного типа,
вторая — к оптимизации в непрерывных пространствах. При
этом возникает определенное противоречие: для генерации
нечетких правил необходимы функции принадлежности, а для
проведения нечеткого вывода — правила. Кроме того, при
автоматической генерации нечетких правил необходимо
обеспечить их полноту и непротиворечивость.
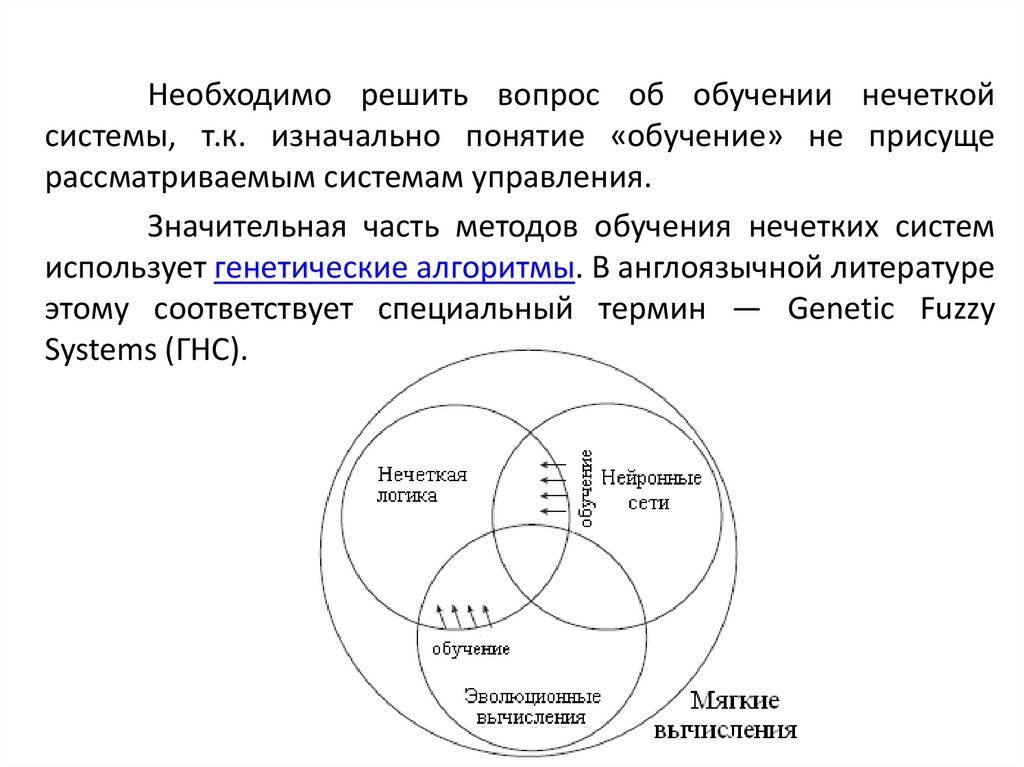
35.
Необходимо решить вопрос об обучении нечеткойсистемы, т.к. изначально понятие «обучение» не присуще
рассматриваемым системам управления.
Значительная часть методов обучения нечетких систем
использует генетические алгоритмы. В англоязычной литературе
этому соответствует специальный термин — Genetic Fuzzy
Systems (ГНС).
36.
ГНС в сущности представляет собой нечеткую систему,расширенную за счет процесса обучения, основанного на
генетическом алгоритме (ГА). Так как ГА являются поисковыми
алгоритмами, которые базируются на естественной генетике,
что обеспечивает способность робастного поиска в сложных
пространствах, то они предлагают обоснованный подход к
решению проблем, требующих эффектных и эффективных
поисковых процессов.
В этой системе ряд параметров находят путем настройки
или обучения, используя ГА.
37.
Принцип работыгенетического алгоритма
Генетический алгоритм — это в первую очередь
эволюционный алгоритм, другими словами, основная фишка
алгоритма — скрещивание (комбинирование). Идея алгоритма
взята у природы. Так вот, путем перебора и самое главное
отбора получается правильная «комбинация».
38.
Алгоритм делится на три этапа:- скрещивание;
- селекция (отбор);
- формирования нового поколения.
Если результат нас не устраивает, эти шаги повторяются
до тех пор, пока результат нас не начнет удовлетворять или
произойдет одно из ниже перечисленных условий:
- количество поколений (циклов) достигнет заранее
выбранного максимума;
- исчерпано время на мутацию.
39.
Практический пример работы ГАНеобходимо решить уравнение типа: a+2b+3c+4d=30.
Возьмем случайные значения a,b,c,d в качестве решения уравнения:
(1,28,15,3)
(14,9,2,4)
(13,5,7,3)
(23,8,16,19)
(9,13,5,2)
40.
Для того чтобы вычислить коэффициенты выживаемости, подставим каждоерешение в выражение. Расстояние от полученного значения до 30 и будет нужным
значением.
- |114-30|=84
- |54-30|=24
- |56-30|=26
- |163-30|=133
- |58-30|=28
Меньшие значения ближе к 30, соответственно они более желанны.
41.
Далее будем выбирать пять пар родителей, у которых будет ровно поодному ребенку. Потомок содержит информацию о генах отца и матери. Это можно
обеспечить различными способами, но в данном случае будет использоваться
«кроссовер». (| = разделительная линия).
Х.-отец: a1 | b1,c1,d1 Х.-мать: a2 | b2,c2,d2 Х.-потомок: a1,b2,c2,d2 or a2,b1,c1,d1
Х.-отец: a1,b1 | c1,d1 Х.-мать: a2,b2 | c2,d2 Х.-потомок: a1,b1,c2,d2 or a2,b2,c1,d1
Х.-отец: a1,b1,c1 | d1 Х.-мать: a2,b2,c2 | d2 Х.-потомок: a1,b1,c1,d2 or a2,b2,c2,d1
Следовательно:
Х.-отец: (13 | 5,7,3) Х.-мать: (1 | 28,15,3) Х.-потомок: (13,28,15,3)
Х.-отец: (9,13 | 5,2) Х.-мать: (14,9 | 2,4) Х.-потомок: (9,13,2,4)
Х.-отец: (13,5,7 | 3) Х.-мать: (9,13,5 | 2) Х.-потомок: (13,5,7,2)
Х.-отец: (14 | 9,2,4) Х.-мать: (9 | 13,5,2) Х.-потомок: (14,13,5,2)
Х.-отец: (13,5 | 7, 3) Х.-мать: (9,13 | 5, 2) Х.-потомок: (13,5,5,2)
42.
Снова вычисляем выживаемость.- (13, 28, 15, 3) — |126-30|=96
- (9, 13, 2, 4) — |57-30|=27
- (13, 5, 7, 2) — |52-30|=22
- (14, 13, 5, 2) — |63-30|=33
- (13, 5, 5, 2) — |46-30|=16
Появилось значение выживаемости равное 16. Алгоритм будет работать до
тех, пор, пока коэффициент выживаемости не будет равен нулю.
43.
Недостатки проектирования нечетких лингвистическихсистем с помощью экспертов:
- не всегда можно найти сведущего эксперта;
- извлечение знаний из эксперта отнимает много
времени;
- системы, построенные на приобретенных с помощью
эксперта знаниях, работают плохо.
Поэтому приходится применять экспериментально
полученные данные для обучения нечеткой системы.
44.
Генетическиеалгоритмы
не
были
специально
разработаны как методы машинного обучения, подобно
нейронным системам. Однако не является секретом, что задача
обучения может быть сформулирована как оптимизационная
задача, и таким образом она может быть решена с помощью
эволюционных алгоритмов.
Так как они обладают большой вычислительной
мощностью для поиска решений задач в сложных плохо
определенных пространствах, то это позволяет успешно
применять ГА для большого круга проблем машинного обучения
и извлечения данных. Присущая им гибкость и способность
встраивать полученные от экспертов знания являются весьма
важным свойством с точки зрения решаемых задач.
45.
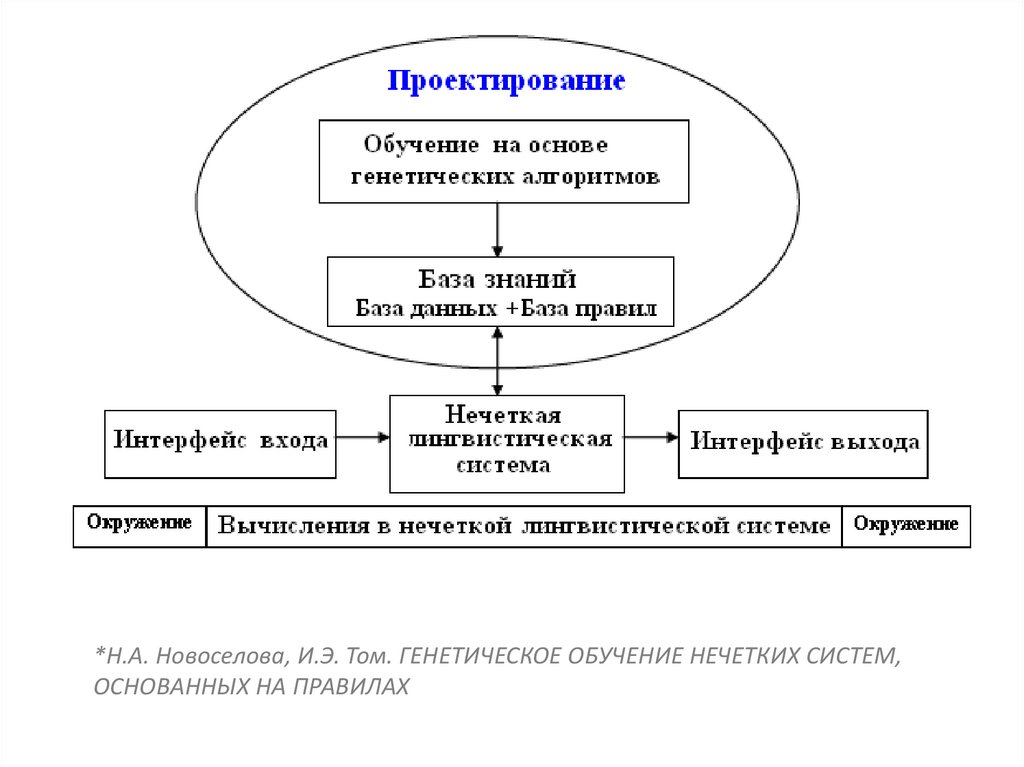
*Н.А. Новоселова, И.Э. Том. ГЕНЕТИЧЕСКОЕ ОБУЧЕНИЕ НЕЧЕТКИХ СИСТЕМ,ОСНОВАННЫХ НА ПРАВИЛАХ
46.
Нечеткая нейронная сеть ANFISAdaptive Network based Fuzzy Inference System
представляет адаптивную систему нейро-нечеткого вывода. С
одной стороны, сеть ANFIS представляет собой нейронную сеть
с единственным выходом и несколькими входами, которые
представляют собой нечеткие лингвистические переменные.
При этом термы входных лингвистических переменных
описываются стандартными функциями принадлежности, а
термы выходной переменной представляются линейной или
постоянной функцией принадлежности. С другой стороны, сеть
ANFIS представляет собой систему нечеткого вывода, в которой
каждое из правил нечетких продукций имеет постоянный вес,
равный 1.
47.
Практический пример48.
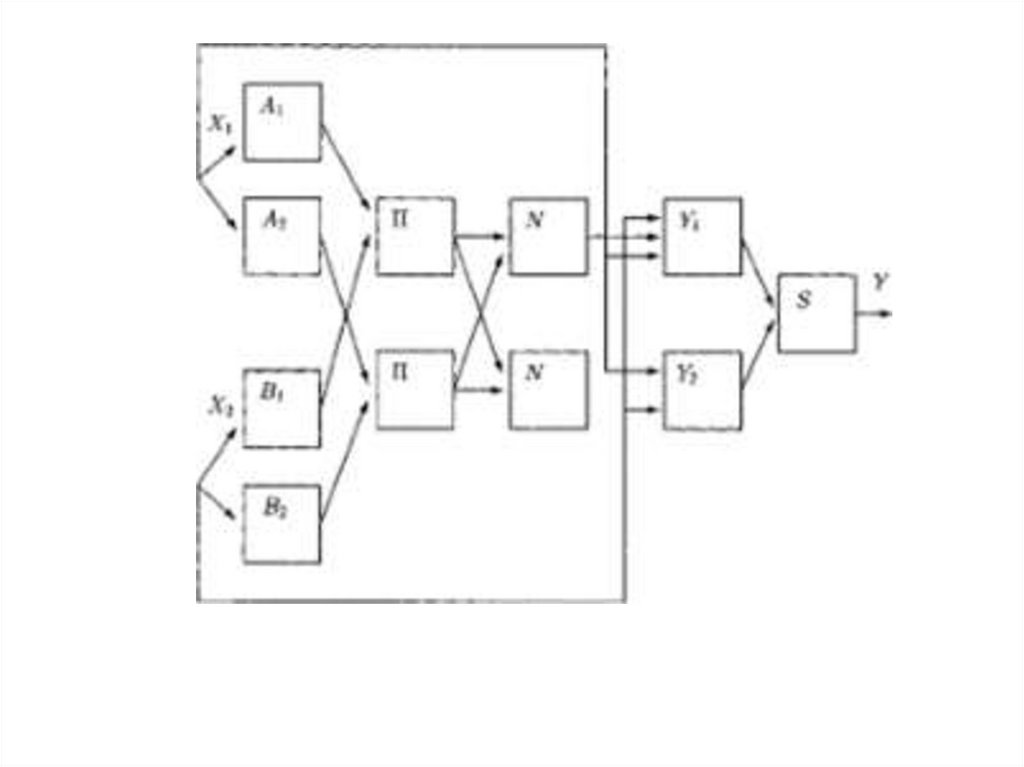
49.
Слой 1: Представлен радиально базисными (РБФ)-нейронами имоделирует функции принадлежности.
Слой 2: Слой «И» нейронов, которые моделируют логическую
связку И произведением w=µA(x1)·µB(x2)·…
Слой 3: Вычисляет нормированную силу правила:
Слой 4: Формирует значение выходной переменной:
Слой 5: Выполняет дефаззификацию:
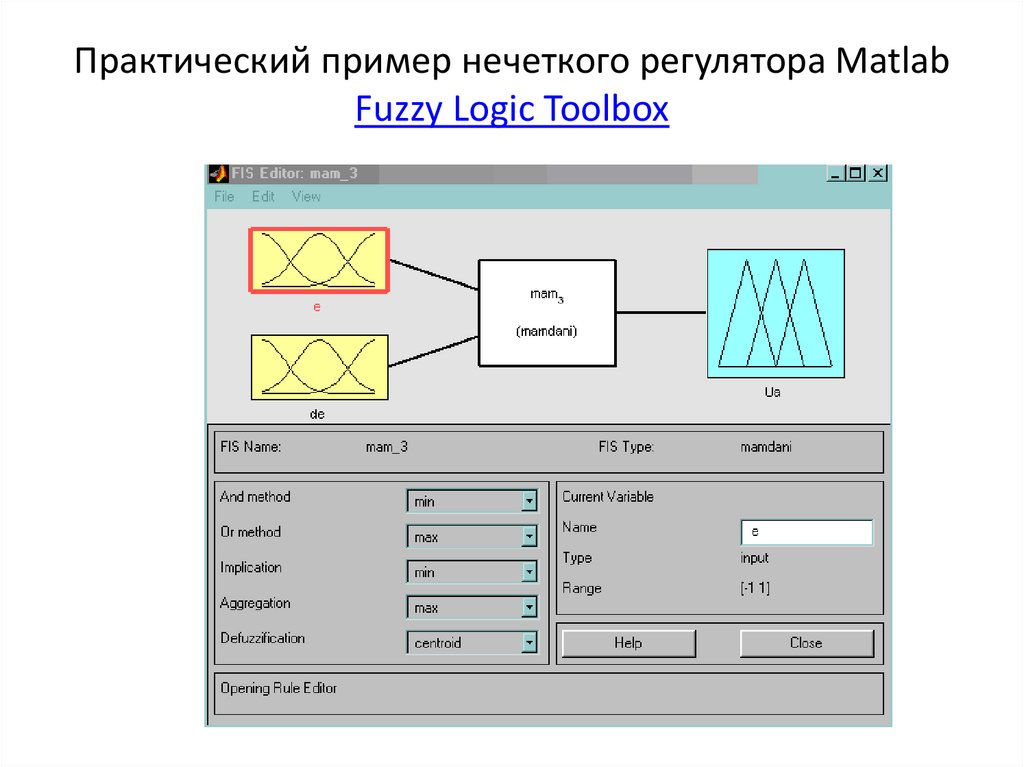
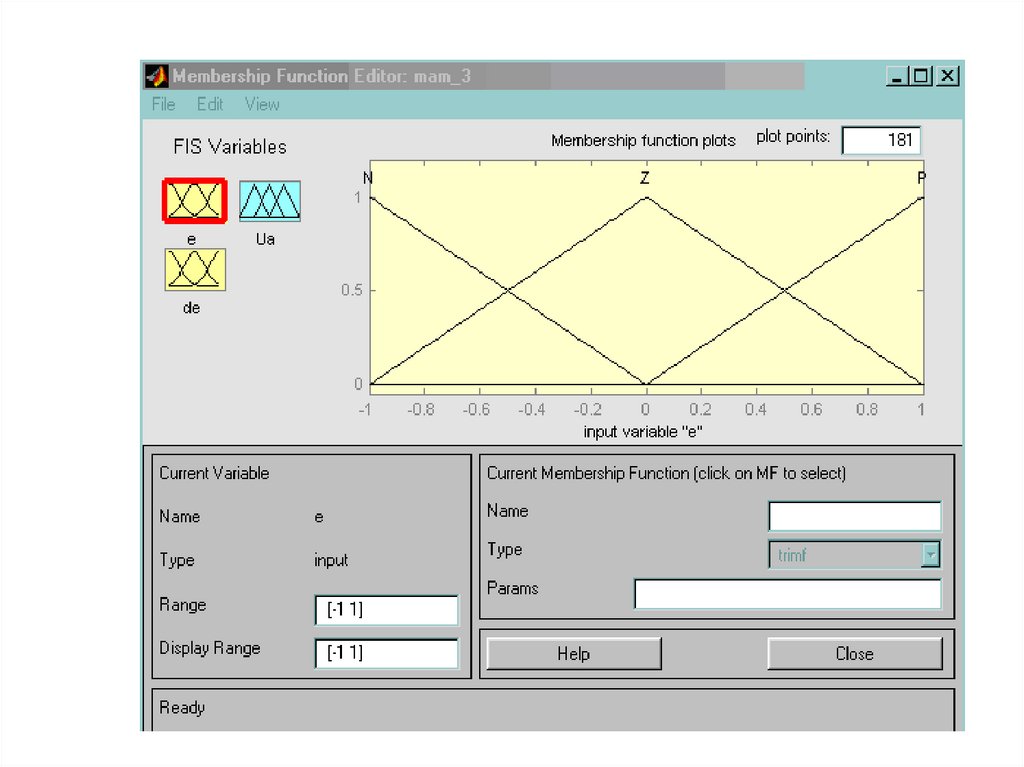
50.
Практический пример нечеткого регулятора MatlabFuzzy Logic Toolbox



































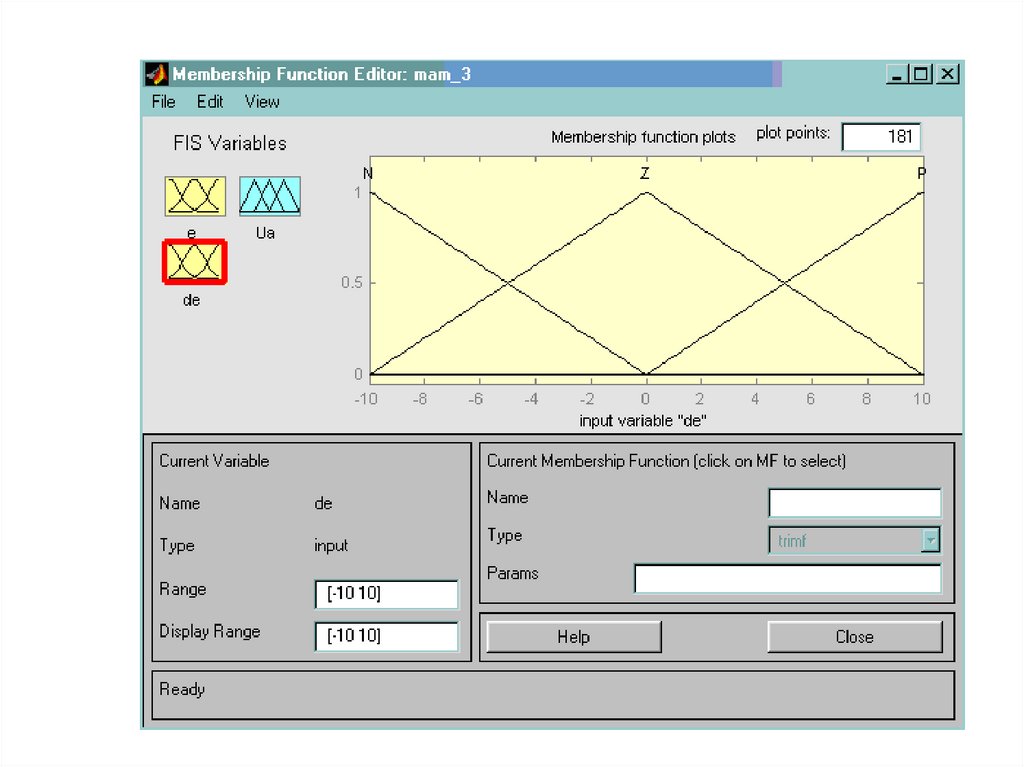
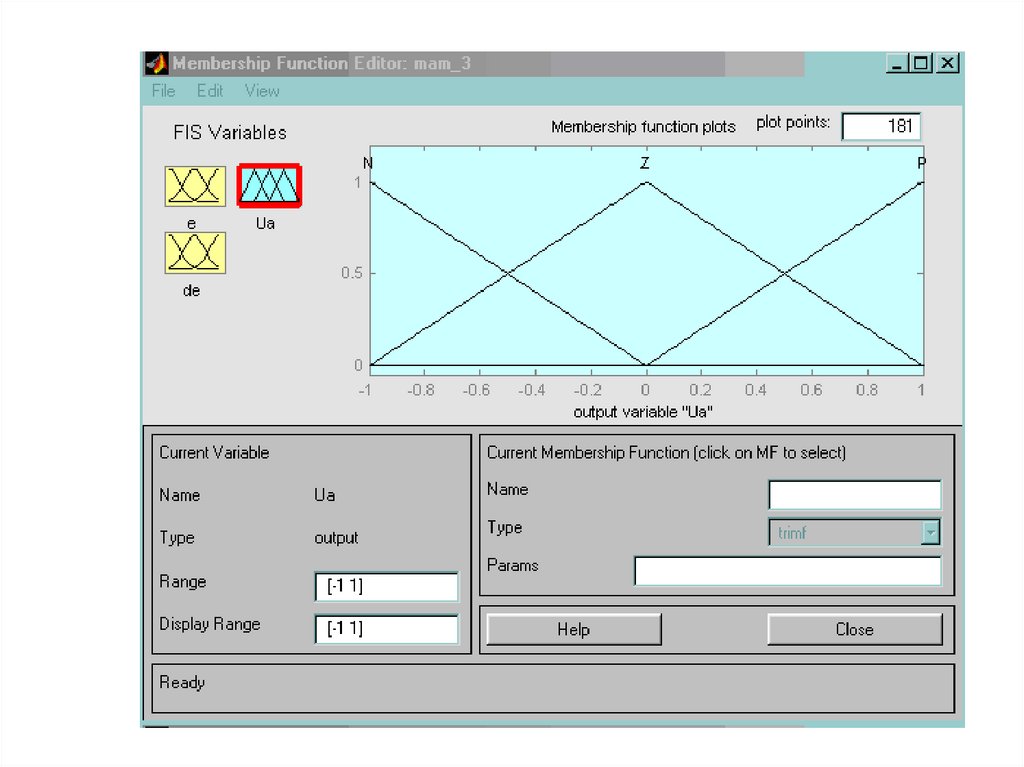
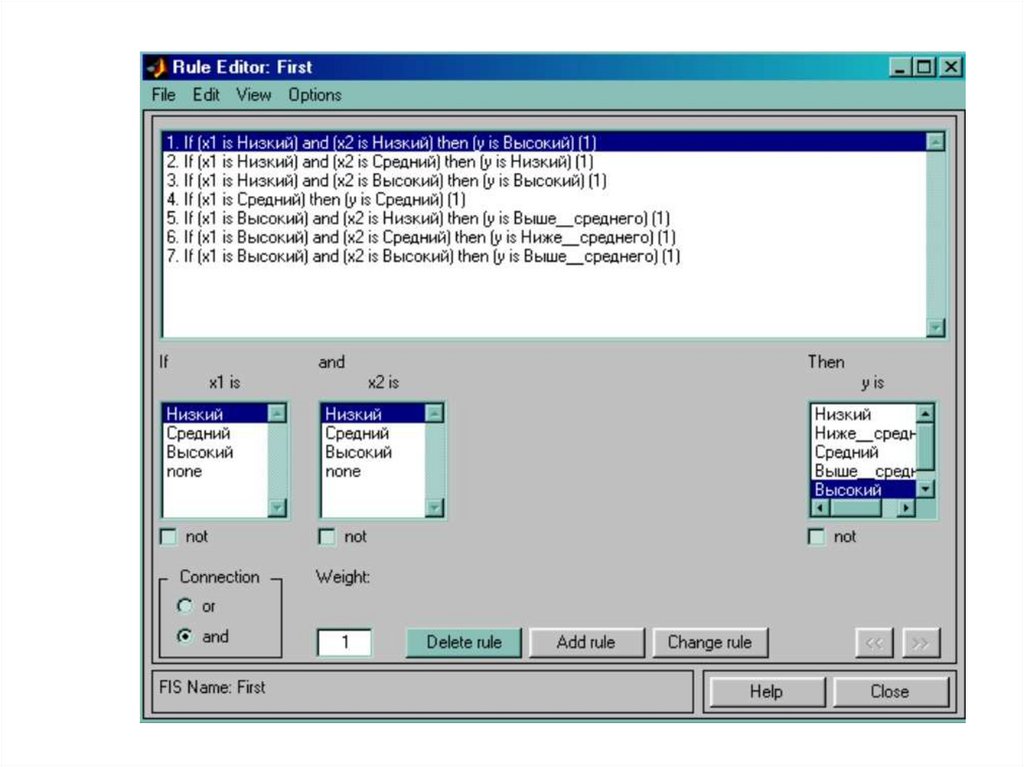
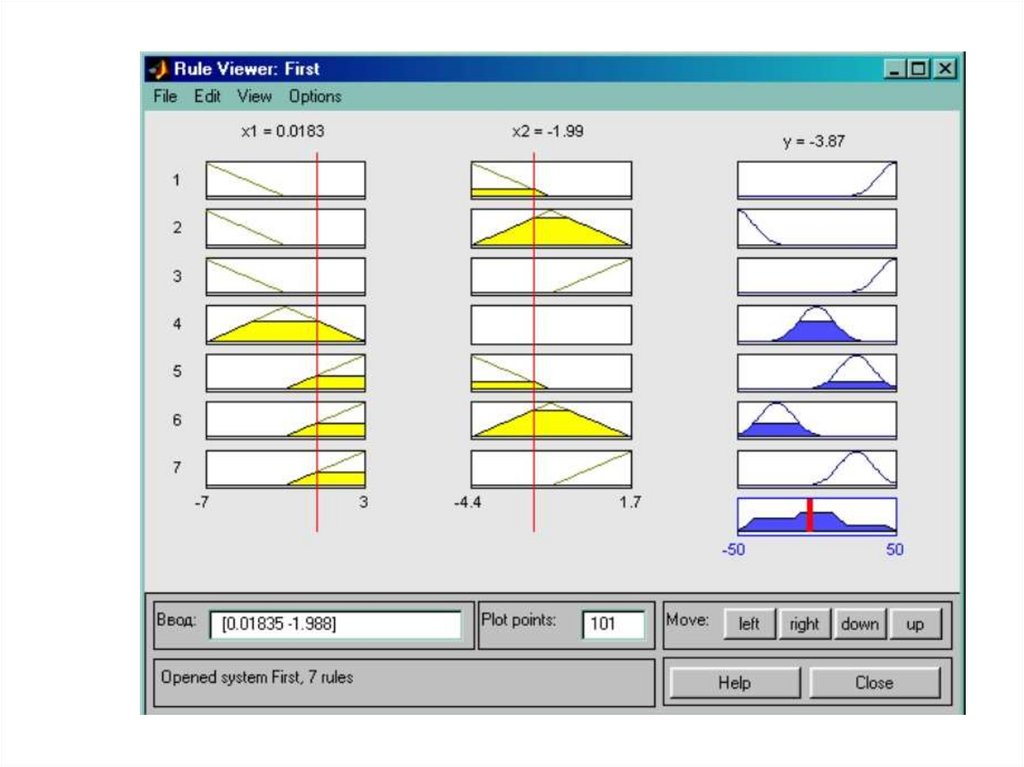
 management
management








