Syllabus overview

1.

Syllabus overview
Course Code
Course Title
Degree Cycle (Level)/
Major
1. General information
PS 2022
Probability and Statistics
Computer Science, Software engineering, Big Data
Analysis, Telecommunication Systems, Cyber Security.
Year, semester
Number of Credits
2nd year, Trimesters: 4, 5, 6
5
Language of Delivery:
English
Prerequisites
Calculus 1, Linear Algebra
Lecturer (Lecturers)
Muslim Zh Sergaziyev, Associate Professor, PhD.
Department of Computational and Data Science.
Email: [email protected]

2.

2. Goals, objectives and learning outcomes of the course
This course covers the fundamental statistical concepts and is
Course
related to the computer science engineering. Topics include:
description
descriptive statistics; probability and random variables;
sampling; statistical distributions; confidence intervals;
hypothesis testing; regression.
Course
goal(s)
Course
objectives:
Introduce students to the theory of probability, including
applications to practical examples;
To develop the students' knowledge and understanding of
statistics.
Course objectives are to teach students how to use statistical
techniques in decision making; to draw correct inferences from
sample data; to formulate appropriate statistical hypotheses;
and to correctly interpret statistical statements. Logical thought
processes are more critical than the ability to manipulate
complex mathematical formulae.

3.

Course
Learning
Outcomes:
Upon successful completion of this course, the student should be able to:
Construct and interpret graphical displays for simple data sets, calculate and
interpret measures for the centre and spread of data;
Compute the probability of various events; describe the concepts of
mutually exclusive events, conditional probability, dependent and
independent events, and Bayes theorem;
Discuss the concepts of random variables, probability distributions,
expected value and variance and identify their use in developing statistical
inference tools;
Describe the concept of a sampling distribution and its use in conducting
statistical inference for population parameters;
Calculate and interpret confidence intervals and hypothesis tests involving
population means, proportions and variance.
Conduct hypothesis testing, including a Chi-Square test of independence,
the concept of P-values in hypothesis testing.
To demonstrate the proper uses of statistical thinking and the role statistics
plays in science.

4.

5.

Lecture and practical sessions plan
Topic and Content
1
Introduction to Statistics, Data Analysis and Probability: sampling procedures,
measures of location, measures of variability, discrete and continuous data, statistical
modelling and graphical methods.
Sample space, events, definitions of probability. Equally likely outcomes.
3
2
[1] Ch.1
[2] Ch.1., Ch.2
Conditional probability, Bayes’ rule. Independent Events.
3
2
[1] Ch. 2,
[2] Ch. 3.
Random Variables. Discrete random variables; Continuous random variables.
Jointly distributed random variables.
3
2
Expectation. Variance. Covariance. Properties of Expectation and Variance. Chebyshev’s
Inequality. The Bernoulli and Binomial Random Variables. Poisson Distribution.
3
2
3
2
Related
chapters SIS
from textbooks [1],
[2]
Pract
Lecture
Week
#
2
3
4
5
The Uniform Random Variable. Exponential Distribution. Normal Random Variable.
Law of large Numbers. The Chi-Squared Distribution. Midterm Exam.
10
10
10
[1] Ch. 3
[2] Ch. 4, Sections:
4.1, 4.2, 4.3
[1] Ch. 4, 5.
10
[2] Ch. 4, Sections:
4.4-4.7,
Ch.5,
Sections: 5.1, 5.2,
5.3.
10
[1] Ch. 6,
[2] Ch. 5, Sections:
5.5, 5.6.
6
Distributions of Sampling Statistics. The sample mean. The Central Limit Theorem. The
sample variance. The t - Distribution. The F - Distribution.
3
2
[1] Ch. 8.
[2] Ch. 6.
10
7
Parameter Estimation. Maximum Likelihood Estimation. Interval Estimates. Confidence
intervals for a normal mean. CI for Bernoulli random variable.
3
2
[1] Ch. 9,
[2] Ch. 7.
10
8
Hypothesis Testing. Significance levels. general concepts, Type I and Type II errors.
Testing means of a Normal Population. p-value, t-Test. Tests on two means.
3
2
[1] Ch. 10,
[2] Ch. 8.
10
9
Regression. Simple linear regression model, least squares and the fitted model,
properties of least squares estimators, inferences for regression coefficients. Endterm
Exam.
3
2
[1] Ch. 11
[2] Ch. 9.
10
10
Residual analysis and model checking, prediction, correlation. Review for final exam.
3
2
[1] Ch. 11
[2] Ch. 9.
10
30
20
Hours in total:
100

6.

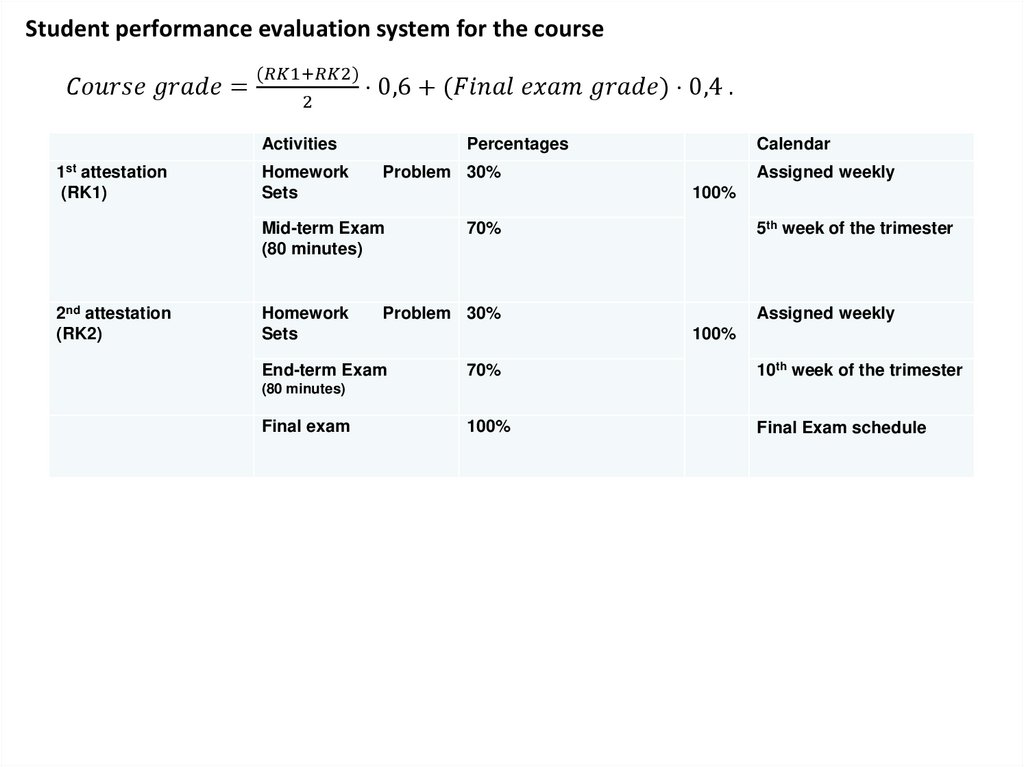
Methods of
Assessment
The expected learning outcomes for the course will be assessed through graded
activities and ungraded activities.
The graded activities include exams, homework assignments, and quizzes.
The ungraded activities will include a monitoring of attendance and class participation.
A variety of ungraded assessment techniques may be employed, that include problems
to be completed during class, direct questioning of students, answering student’s
questions in class, and discussions during office hours.

7.

Student performance evaluation system for the course