Similar presentations:
Курс общей физики
1. Курс общей физики
КУРСОБЩЕЙ
ФИЗИКИ
ЛЕКЦИЯ 6
МОЛЕКУЛЯРНО-КИНЕТИЧЕСКАЯ ТЕОРИЯ ИДЕАЛЬНОГО ГАЗА
2. МОЛЕКУЛЯРНО-КИНЕТИЧЕСКАЯ ТЕОРИЯ ИДЕАЛЬНОГО ГАЗА
Молекулярная физика – это наука, которая изучает физические свойства иагрегатные состояния тел в зависимости от их молекулярного строения, сил
взаимодействия между частицами и характера теплового движения частиц.
Для теоретического изучения вопросов молекулярной физики используются
взаимодополняющих метода – статистический и термодинамический.
два
Статистический метод состоит в изучении свойств макроскопических систем на
основе анализа закономерностей теплового движения большого количества
микрочастиц составляющих систему с помощью методов математической
статистики.
Макроскопическая система – это система состоящая из очень большого числа
частиц.
Термодинамический метод основывается на изучении свойств системы
взаимодействующих тел путем анализа условий и количественных соотношений
преобразования энергии, происходящих в системе.
3. ОСНОВНЫЕ ПОЛОЖЕНИЯ МКТ
1. Все тела состоят из мельчайших частиц атомов имолекул
2. Частицы находятся в непрерывном беспорядочном
хаотическом движении,
которое
называется
тепловым движением
3. Между
частицами
вещества
действуют
силы
притяжения и отталкивания, зависящие от расстояния
между частицами
4. ОСНОВНЫЕ ПОЛОЖЕНИЯ МКТ
Данныеположения
подтверждаются
благодаря
следующим
экспериментальным
результатам.
Наличие
молекул
подтверждается
возможностью механического дробления вещества, растворением веществ в
растворителях. Явление диффузии свидетельствует о том, что между
молекулами газов, жидкостей и твердых тел есть промежутки – вещество
дискретно. При смешивании различных жидкостей и растворении твердых тел
в жидкости объем смеси может отличаться от объема смешиваемых
компонент, что свидетельствует о различных размерах молекул. Т.к. газ
занимает любой предоставленный ему объем, то молекулы газа движутся
независимо друг от друга, хаотически, непрерывно, а любое направление
движения молекул равновероятно.
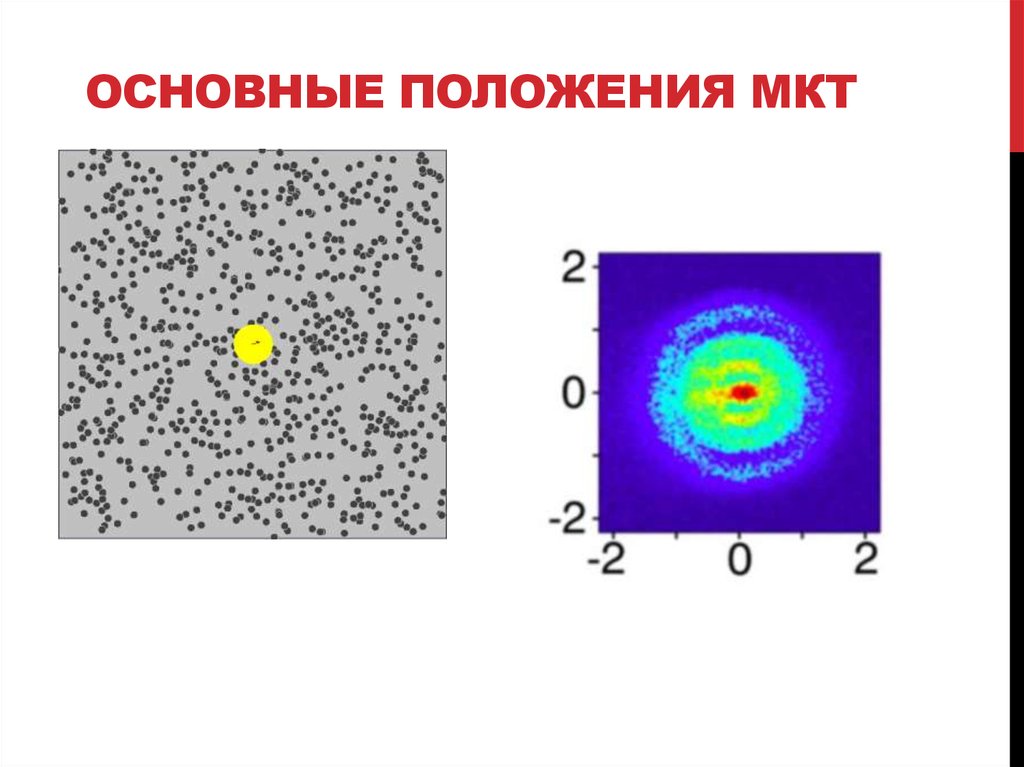
Наиярчайшее подтверждение непрерывного хаотического движения молекул
– броуновское движение. При размерах броуновских частичек ~10-4 – 10-5 м
число ударов молекул жидкости о них не будет слишком большим и начнут
проявляться отклонения числа ударов молекул в отдельные стороны частички
от средних значений. Говорят, что наблюдаются флуктуации скорости
броуновской частицы.
Флуктуации – это отклонение тех или иных величин от их средних
значений, которые происходят в малых объемах или на протяжении
малых промежутков времени.
5. ОСНОВНЫЕ ПОЛОЖЕНИЯ МКТ
6. ОСНОВНЫЕ ПОЛОЖЕНИЯ МКТ
Количество молекул в любом самом небольшом объеме вещества велико:при условии T=273 K и p=1,01∙105 Па (нормальные условия) в 1 см3 воздуха
содержится n0 = 2.69∙1019 молекул. n0 называется числом Лошмидта.
О наличии сил отталкивания свидетельствуют малая сжимаемость
жидкостей и твердых тел, упругость сжатых газов. Действие сил притяжения
между молекулами подтверждается тем, что твердые тела сохраняют свою
форму и для их разрушения необходимо приложение силы.
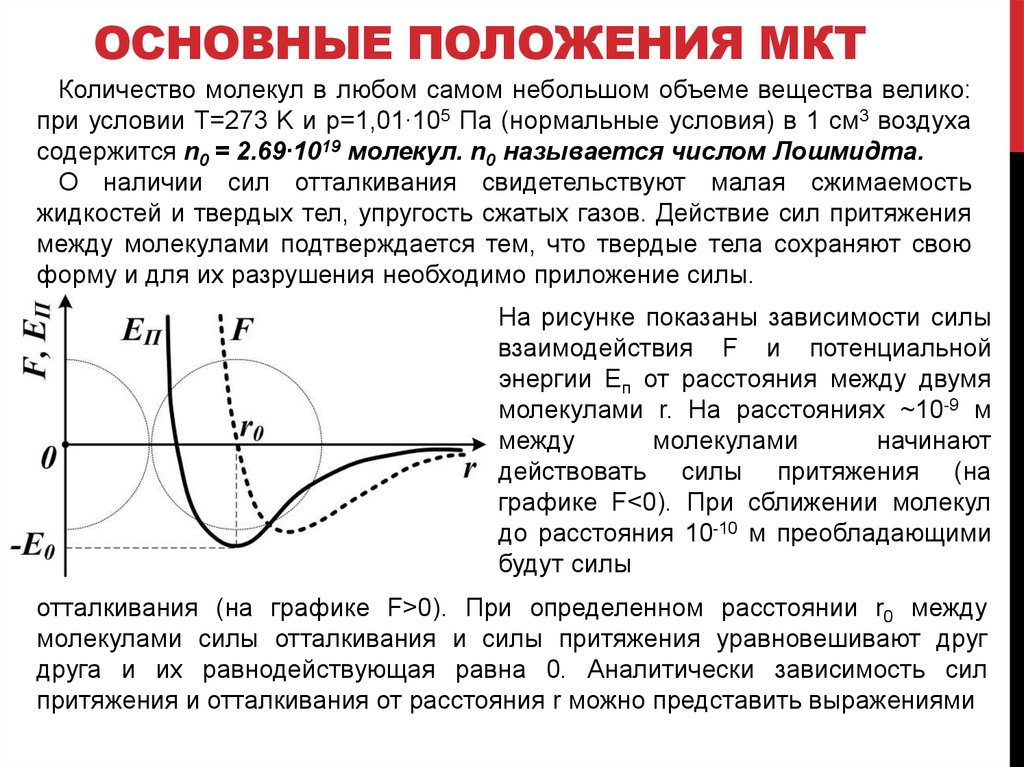
На рисунке показаны зависимости силы
взаимодействия F и потенциальной
энергии Eп от расстояния между двумя
молекулами r. На расстояниях ~10-9 м
между
молекулами
начинают
действовать силы притяжения (на
графике F<0). При сближении молекул
до расстояния 10-10 м преобладающими
будут силы
отталкивания (на графике F>0). При определенном расстоянии r0 между
молекулами силы отталкивания и силы притяжения уравновешивают друг
друга и их равнодействующая равна 0. Аналитически зависимость сил
притяжения и отталкивания от расстояния r можно представить выражениями
7. ОСНОВНЫЕ ПОЛОЖЕНИЯ МКТ
Fï ðèò ÿæ åí èÿa
b
,
F
,
î ò ò àëêèâàí èÿ
n
m
r
r
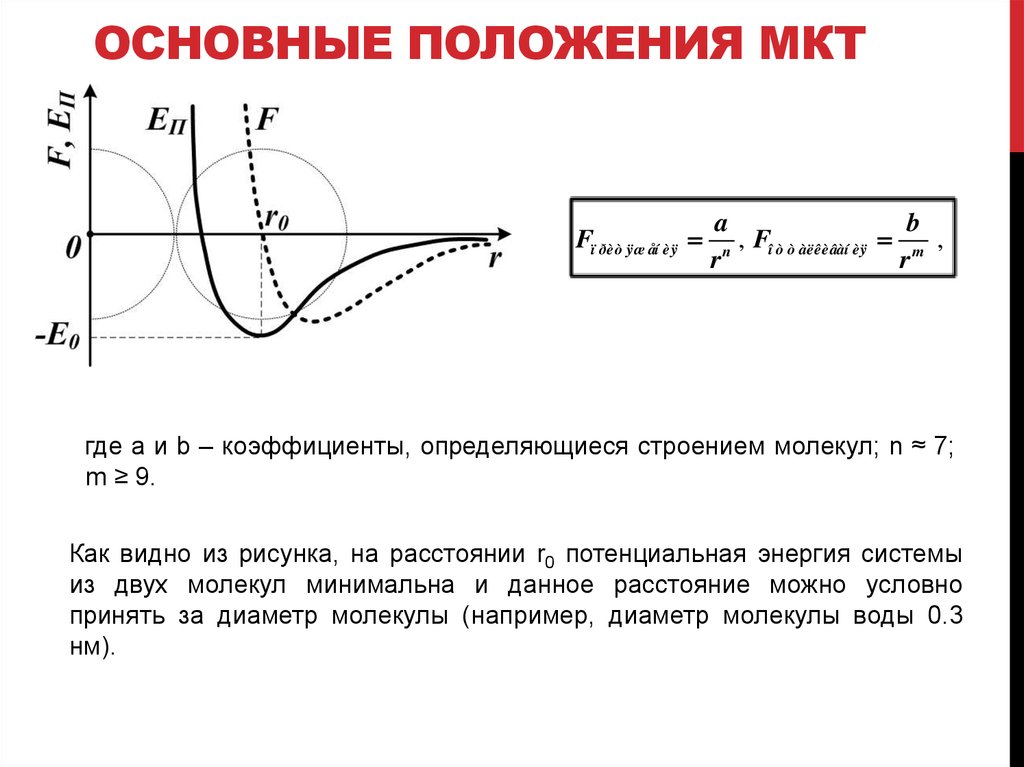
где a и b – коэффициенты, определяющиеся строением молекул; n ≈ 7;
m ≥ 9.
Как видно из рисунка, на расстоянии r0 потенциальная энергия системы
из двух молекул минимальна и данное расстояние можно условно
принять за диаметр молекулы (например, диаметр молекулы воды 0.3
нм).
8. ИДЕАЛЬНЫЙ ГАЗ
Любое вещество представляет некоторую систему, состоящую из множествачастиц. Из повседневного опыта следует, что одно и то же вещество при разных
условиях может иметь различные свойства, т.е. система может находится в
различных состояниях. Переход системы из одного состояния в другое
называется процессом. Изменение состояния системы сопровождается
изменением некоторых физических величин, называемых параметрами
состояния. Параметров состояния системы три: давление p, плотность r и
температура Т. Однако, учитывая что во многих случаях масса системы
неизменна, чаще вместо плотности r используют объем V.
Для упрощения рассмотрения процессов, которые происходят в системе
пользуются идеализированным понятием «идеальный газ». Идеальный газ –
это система материальных точек, между которыми совершенно
отсутствует притяжение. Приближенно любой газ в разряженном
состоянии (т.е. при малых давлениях и достаточно высокой температуре) можно
рассматривать как идеальный. В таком случае размеры молекул значительно
меньше среднего расстояния между ними. Единственно возможным
взаимодействием молекул идеального газа является их взаимное отталкивание
при соударении. Такое взаимодействие подобно соударяющимся упругим
шарикам.
9. Теплота как форма энергии. Температура.
ТЕПЛОТА КАК ФОРМА ЭНЕРГИИ.ТЕМПЕРАТУРА.
Теплота — это особая форма энергии, с которой связано беспорядочное
движение микроскопических частиц вещества. Данная связь следует,
например, из наблюдаемой в опыте зависимости броуновского движения от
количества сообщенного телу тепла.
Температура — макроскопическая характеристика теплового движения.
Значит температура является мерой содержащегося в теле тепла и
определяет направление перехода тепла — от более нагретого тела к менее
нагретому.
10. Теплота как форма энергии. Температура.
ТЕПЛОТА КАК ФОРМА ЭНЕРГИИ.ТЕМПЕРАТУРА.
Очевидно, что т.к. теплота является одной из форм энергии, то должна
существовать ее связь с кинетической энергией частиц. Чем больше нагрето
тело, тем больше и кинетическая энергия его частиц. Т.о., как кинетическую
энергию движения частиц так и температуру, можно рассматривать как меру
теплового движения.
Отметим, что температура — это макроскопическая характеристика тела,
тогда как кинетическая энергия соответствует отдельной частице. Тогда
температура должна быть связана со средней кинетической энергией,
приходящейся на одну частицу в системе большого числа частиц (здесь под
системой понимается идеальный газ). Обозначим среднюю кинетическую
энергию частицы в системе из N составляющих символом <Ek> и
определим ее выражением
Ek
1
N
mi i2
,
2
i= 1
N
где mi – масса i-й частицы системы; i – скорость i-й частицы системы.
11. Теплота как форма энергии. Температура
ТЕПЛОТА КАК ФОРМА ЭНЕРГИИ.ТЕМПЕРАТУРА
В случае, если масса всех частиц системы одинакова, данное выражение
можно записать в виде
Ek
где
êâ
N
i2
N
m
2N
N
1
2
m
,
êâ
2
i= 1
2
i
– среднеквадратичная или тепловая скорость частиц.
i= 1
Пусть T
2
1
Ek m 2 .
êâ
3
3
Чтобы выразить температуру в Кельвинах, нужно знать коэффициент
пропорциональности, показывающий, сколько джоулей соответствует одному
Кельвину. Такой коэффициент называют постоянной Больцмана и, как
следует из измерений, равен 1.38·10-23 Дж/К, где К означает Кельвин. Тогда
соотношение между температурой в и энергией запишется как
Ek
3
kT , где k – константа Больцмана.
2
12. Теплота как форма энергии. Температура
ТЕПЛОТА КАК ФОРМА ЭНЕРГИИ.ТЕМПЕРАТУРА
Полученная формула выражает среднюю кинетическую энергию
поступательного движения молекулы массой m.
Подчеркнем, что температуры имеет статистический характер, т.к. она
связана со средней энергией частиц. Отсюда можно говорить лишь о
температуре
системы
достаточно
большого
числа
частиц
—
макроскопической системы, и нельзя говорить о температуре одной или
десяти частиц. При измерении температуры происходит обмен теплом
между системой частиц и измерительным прибором термометром. Понятие
температуры тела приобретает смысл в том случае, если обмен теплом
между телом и прибором в процессе измерения температуры мало
изменяет состояние тела.
13. Давление идеального газа. Основное уравнение МКТ
ДАВЛЕНИЕ ИДЕАЛЬНОГО ГАЗА.ОСНОВНОЕ УРАВНЕНИЕ МКТ
Пусть в сосуде в виде прямоугольного параллелепипеда находится N
молекул идеального газа, а стенки сосуда – «идеально, отражающими».
Будем считать, что при отражении от стенки скорость молекулы не меняется
по величине, а меняется лишь по направлению. После удара о стенку
молекулы, проекция скорости которой до удара на направлении оси x равна
x, проекция изменится и станет - x. Значит импульс в том же направлении
изменится на Dpx = 2·m· x.
Далее молекула долетит до противоположной стенки, отразится от нее и
снова ударится о первую стенку. Время между ударами будет Δt = 2ℓ/( x), а
число ударов за 1 с n = 1/Δt = x/(2ℓ). За 1 с молекула сообщит стенке
импульс в проекции на ось x
nx D p 2m x
x
2
m x2
14. Давление идеального газа. Основное уравнение МКТ
ДАВЛЕНИЕ ИДЕАЛЬНОГО ГАЗА.ОСНОВНОЕ УРАВНЕНИЕ МКТ
Согласно 2 закону Ньютона импульс, передаваемый за единицу времени
стенке, равен силе, с которой данная молекула действует на стенку. Значит
i-я молекула действует на стенку с силой, проекция которой на ось x равна
Fix = m 2ix/ℓ.
На данную стенку в направлении оси х в некоторый момент времени
действуют множество частиц, что можно выразить как
N
N
Fx Fix
i=1
m
2
ix
mN
i=1
N
2
ix
N
m N 2
êâ
i=1
Учитывая, что сила Fx отнесенная к площади стенки S имеет смысл
давления, получим
P
Fx
S
m N 2
êâ
S
m N 2
êâ
V
, где V – объем сосуда.
15. Давление идеального газа. Основное уравнение МКТ
ДАВЛЕНИЕ ИДЕАЛЬНОГО ГАЗА.ОСНОВНОЕ УРАВНЕНИЕ МКТ
Заметим, что в условиях теплового равновесия все направления движения в
сосуде равноправны. Это значит, что на каждое направление движения
приходится одинаковое количество молекул в некоторый момент времени.
Таких направлений 3: x, y, z. Поэтому на направление оси х будет
приходиться 1/3 от всех молекул сосуда. Отсюда давление, оказываемое
газом на одну стенку запишется выражением
2 N m 2
êâ
P
3 V
2
Соотношение
2
n Ek , где n – концентрация молекул газа
3
в сосуде.
2
P n Ek
3
называется основным уравнением молекулярно-кинетической теории газов.
16. Распределение Максвелла
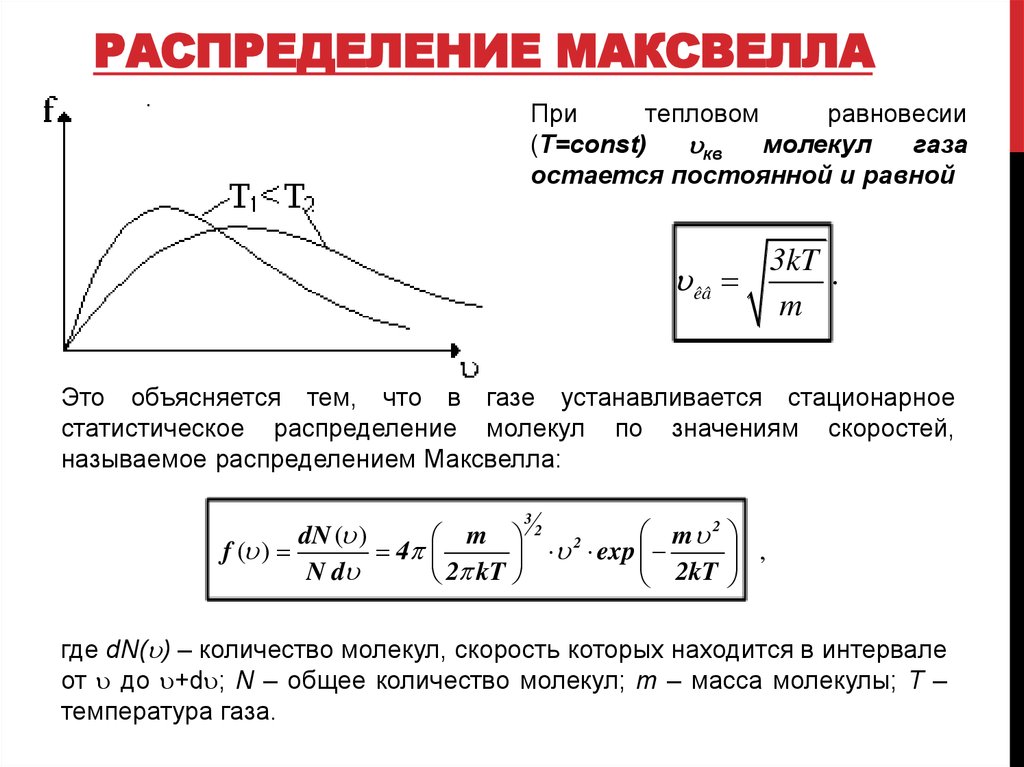
РАСПРЕДЕЛЕНИЕ МАКСВЕЛЛАПри
тепловом
равновесии
(Т=cоnst)
кв
молекул
газа
остается постоянной и равной
3kT
êâ
m
Это объясняется тем, что в газе устанавливается стационарное
статистическое распределение молекул по значениям скоростей,
называемое распределением Максвелла:
3
m 2
dN ( )
m 2 2
f ( )
4
,
exp
N d
2
kT
2kT
где dN( ) – количество молекул, скорость которых находится в интервале
от до +d ; N – общее количество молекул; m – масса молекулы; T –
температура газа.
17. Распределение Максвелла
РАСПРЕДЕЛЕНИЕ МАКСВЕЛЛАТ.о., f( ) равна вероятности того, что величина скорости наугад выбранной
молекулы принадлежит единичному интервалу скоростей вблизи значения .
Из рисунка следует, что f(0) стремится к 0 при =0 и →∞ и проходит через
максимум при некоторой скорости в, называемой наиболее вероятной
скоростью. Этой скоростью и близкой к ней обладает наибольшее
количество молекул. Из условия для максимума функции f( ) значение в
равно
â
2kT
2RT
m
Знание f( ) молекул газа позволяет вычислять средние значения любых
функций скорости, например средней арифметической скорости < >
f( ) d
0
8kT
8RT
m
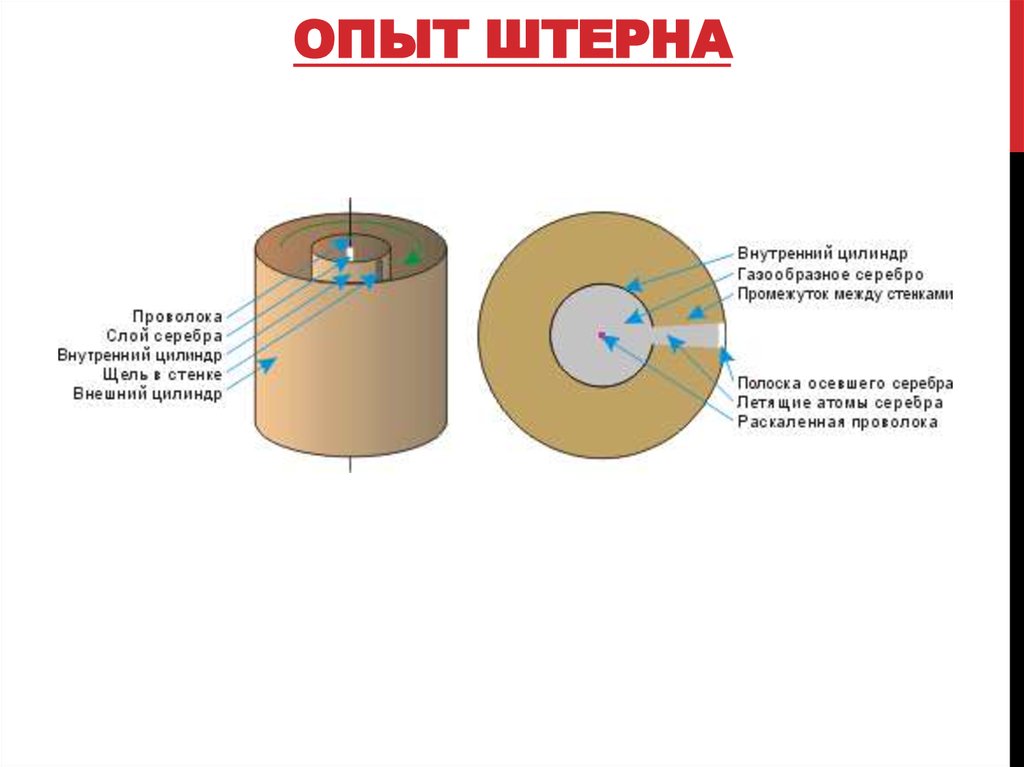
18. ОПЫТ ШТЕРНА
19. Барометрическая формула
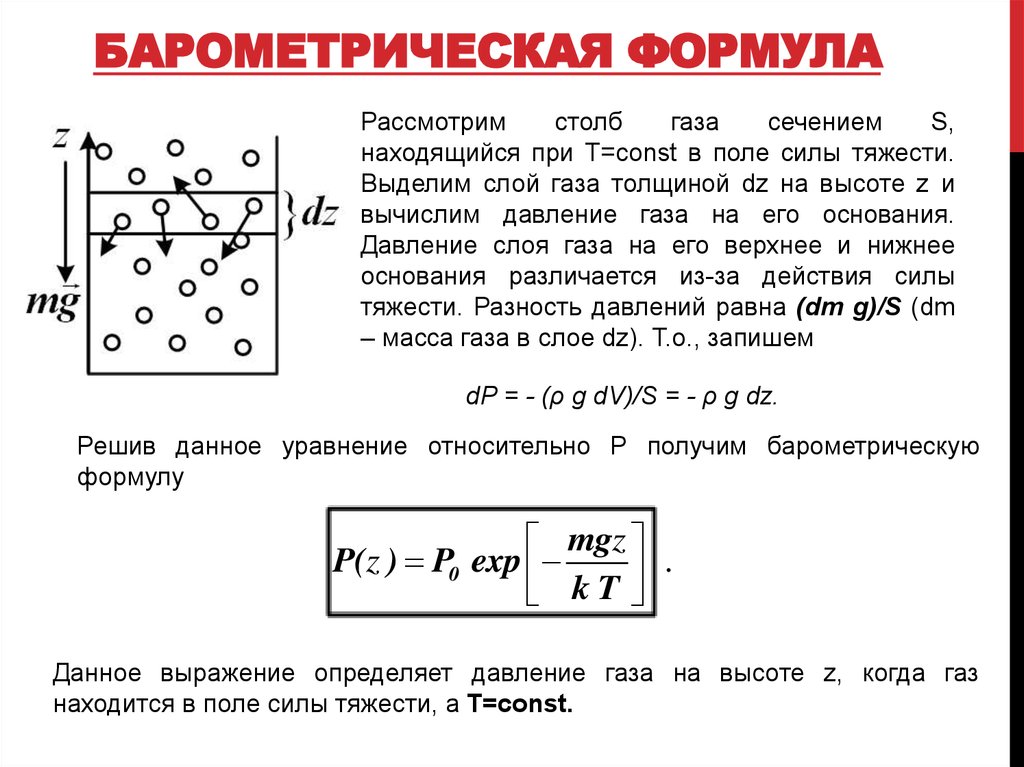
БАРОМЕТРИЧЕСКАЯ ФОРМУЛАРассмотрим
столб
газа
сечением
S,
находящийся при T=const в поле силы тяжести.
Выделим слой газа толщиной dz на высоте z и
вычислим давление газа на его основания.
Давление слоя газа на его верхнее и нижнее
основания различается из-за действия силы
тяжести. Разность давлений равна (dm g)/S (dm
– масса газа в слое dz). Т.о., запишем
dP = - (ρ g dV)/S = - ρ g dz.
Решив данное уравнение относительно P получим барометрическую
формулу
mgz
P(z ) P0 exp
.
kT
Данное выражение определяет давление газа на высоте z, когда газ
находится в поле силы тяжести, а Т=const.
20. Распределение Больцмана
РАСПРЕДЕЛЕНИЕ БОЛЬЦМАНАПользуясь барометрической формулой и уравнением состояния
идеального газа легко получить, что концентрация молекул газа в
потенциальном поле сил в пространстве изменяется как
Ep( r )
n( r )=no exp ,
kT
где n0 концентрация молекул с нулевой потенциальной энергией Ep.
Данное выражение называют распределение Больцмана.
Согласно распределению Больцмана число частиц, обладающих
определенными значениями потенциальной энергии определяется
отношением величины потенциальной энергии и kT. Чем больше энергия
теплового движения, тем более разупорядочена система частиц, значит,
тем более однородно распределены частицы в пространстве. В случае
kT << Ep распределение частиц максимально упорядочено: плотность
частиц максимальная в состоянии с минимальной потенциальной
энергией, в то время как плотность частиц в других состояниях равна
нулю.
21. Внутренняя энергия. Внутренняя энергия идеального газа. Закон равномерного распределения энергии по степеням свободы
ВНУТРЕННЯЯЭНЕРГИЯ.
ВНУТРЕННЯЯ
ЭНЕРГИЯ
ИДЕАЛЬНОГО
ГАЗА.
ЗАКОН
РАВНОМЕРНОГО
РАСПРЕДЕЛЕНИЯ ЭНЕРГИИ ПО СТЕПЕНЯМ СВОБОДЫ
Внутренняя энергия является важной характеристикой состояния
системы и определяется как среднее значение полной энергии ее
частиц. Выделяют следующие составляющие внутренней энергии:
- энергия поступательного, вращательного и колебательного движений
атомов и молекул;
- энергия межмолекулярного взаимодействия;
- энергия связи атомов в молекулах (химическая энергия);
- энергия связи электронов в атомах;
- энергия связи атомных ядер и др.
Внутренняя энергия имеет следующие свойства:
- в состоянии теплового равновесия движение частиц системы таково, что в
любой момент времени среднее значение полной энергии частиц с высокой
степенью точности равняется внутренней энергии (статистические
флуктуации очень малы);
- является функцией термодинамических параметров;
- обладает свойством аддитивности.
22. Внутренняя энергия. Внутренняя энергия идеального газа. Закон равномерного распределения энергии по степеням свободы
ВНУТРЕННЯЯЭНЕРГИЯ.
ВНУТРЕННЯЯ
ЭНЕРГИЯ
ИДЕАЛЬНОГО
ГАЗА.
ЗАКОН
РАВНОМЕРНОГО
РАСПРЕДЕЛЕНИЯ ЭНЕРГИИ ПО СТЕПЕНЯМ СВОБОДЫ
Внутренняя энергия идеального газа в равновесном состоянии является
суммой энергий поступательного, вращательного и колебательного движений
атомов и молекул. При нормальных условиях для вычисления внутренней
энергии используют закон равнораспределения энергии по степеням
свободы:
В состоянии теплового равновесия на каждую поступательную и
вращательную степень свободы в среднем приходится энергия, равная
кТ / 2, а на колебательную – кТ.
Число степеней свободы i – это минимальное количество координат,
однозначно
определяющих положение
механической
системы
в
пространстве (или количество независимых движений, благодаря которым
тело обладает энергией).
23. Внутренняя энергия. Внутренняя энергия идеального газа. Закон равномерного распределения энергии по степеням свободы
ВНУТРЕННЯЯЭНЕРГИЯ.
ВНУТРЕННЯЯ
ЭНЕРГИЯ
ИДЕАЛЬНОГО
ГАЗА.
ЗАКОН
РАВНОМЕРНОГО
РАСПРЕДЕЛЕНИЯ ЭНЕРГИИ ПО СТЕПЕНЯМ СВОБОДЫ
Средняя энергия молекулы может быть представлена как
E
i nï î ñò + nâðàù +2 nêî ëåá
i
kT , где
2
– количество степеней свободы
молекулы.
Для идеального газа массой m внутренняя энергия может быть
выражена как
i m
U RT .
2

















 physics
physics








