Similar presentations:
5 платоновых тел
1.
Выполнил: Черемных ДенисИс(Тп-11)
5
Платоновых тел
2.
БиографияПлатона
Этот выдающийся древнегреческий
мыслитель вошел в историю не под своим
настоящим именем, а под прозвищем
(«Платон» означает ‘широкий’), данным ему то
ли за широкий лоб, то ли за широту ума, то ли
за крепкое телосложение. Настоящее же имя
мальчика, родившегося в 427 году до нашей
эры, — Аристокл. Биография Платона с
рождения складывалась благоприятно. Он
появился в аристократической афинской
семье. Отец Аристон был потомком
легендарного царя Аттики Кодра. Мать
Периктиона происходила из рода поэта,
мудреца и афинского политика Солона, а сама
была писательницей.
3.
Детство и юностьУ семьи была возможность дать сыну превосходное образование:
Первый учитель Платона — философ Кратил дал ему основы всех знаний. С детства
будущий мыслитель занимался рисованием, музыкой, стихосложением. Развивался
физически, занимаясь гимнастикой. Сохранились сведения о его победах на
олимпийских играх.
Уже в зрелые годы Платон благодарил небеса за то, что был гражданином Афин,
родился мужчиной, а главное — что был современником Сократа.
В возрасте 20 лет Платон знакомится с этим выдающимся философом и становится его
учеником. Сократ тоже рассмотрел в юноше будущего гения. Известно, что Сократ не
оставил письменных трудов, все его идеи изложены талантливым учеником. Оба
мыслителя — Сократ и Платон — были приверженцами диалектики и диалогов.
4.
Платон: философия, афоризмыКто такой Платон в мире
философии? Ученые до него
изучали видимый мир,
воспринимаемый органами
чувств. Позже их назвали
материалистами. Платон открыл
другую реальность — мир идей.
Его позиция породила целое
направление в философии —
объективный идеализм. Платон
основные труды посвятил
осмыслению таких проблем:
5.
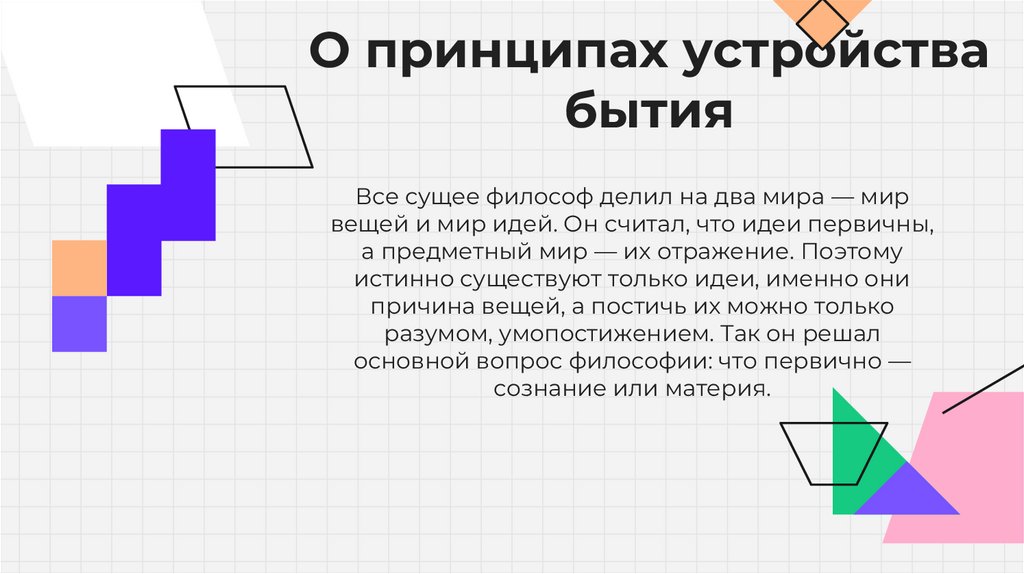
О принципах устройствабытия
Все сущее философ делил на два мира — мир
вещей и мир идей. Он считал, что идеи первичны,
а предметный мир — их отражение. Поэтому
истинно существуют только идеи, именно они
причина вещей, а постичь их можно только
разумом, умопостижением. Так он решал
основной вопрос философии: что первично —
сознание или материя.
6.
Какова связь с Платоном?Вероятнее всего Древнегреческий ученый
Платон не имеет отношения к открытию этих
замечательных многогранников.
Но у Платона был другой дар.
В современном мире можно было бы назвать
Платона популяризатором правильных
многогранников. Наибольший вклад Платон
сделал именно в том, что рассказал людям о
существовании таких предметов как правильные
многогранники.
И, возможно, если бы просто рассказал, то
большинство бы быстро забыло о них. Платон же
наделил эти, казалось бы, простые предметы
невероятной силой, мистическим смыслом и
возвел на вершину своего учения.
В попытке объяснить природу
всего сущего Платон посчитал
пять правильных
многогранников
первоосновами для строения
каждой из стихий:
- огонь - соотносился с
тетраэдром;
- воздух – соотносился с
октаэдром;
- земля – соотносилась с
гексаэдром;
- вода – с икосаэдром;
- а додекаэдр - соответствовал
Вселенной.
7.
Доказательство того, что существует ровнопять правильных выпуклых многогранников
Очевидно, что каждая вершина многогранника может принадлежать трем и
более граням. Сначала рассмотрим случай, когда грани многогранника равносторонние треугольники. Поскольку внутренний угол
равностороннего треугольника равен 60°, три таких угла, помещенные на
плоскость, дадут в сумме 180°. Если теперь согнуть эти углы по внутренним
сторонам и склеить по внешним, получим многогранный угол тетраэдра –
правильного многогранника, в каждой вершине которого встречаются три
правильные треугольные грани. Три правильных треугольника с общей
вершиной называется разверткой вершины тетраэдра. Если добавить к
развертке вершины еще один треугольник, в сумме получится 240°. Это
развертка вершины октаэдра. Добавление пятого треугольника даст угол
300° - мы получаем развертку вершины икосаэдра. Если же добавить еще
один, шестой треугольник, сумма углов станет равной 360° - эта развертка,
очевидно, не может соответствовать ни одному выпуклому многограннику.
8.
Доказательство того, что существует ровнопять правильных выпуклых многогранников
Теперь перейдем к квадратным граням. Развертка из трех квадратных граней имеет
угол 3x90°=270° - получается вершина куба, который также называют гексаэдром.
Добавление еще одного квадрата увеличит угол до 360° - этой развертке уже не
соответствует никакой выпуклый многогранник.
Три пятиугольные грани дают угол развертки 3*108°=324° - вершина додекаэдра. Если
добавить еще один пятиугольник, получим больше 360°.
Для шестиугольников уже три грани дают угол развертки 3*120°=360°, поэтому
правильного выпуклого многогранника с шестиугольными гранями не существует. Если
же грань имеет еще больше углов, то развертка будет иметь еще больший угол. Значит,
правильных выпуклых многогранников с гранями, имеющими шесть и более углов, не
существует.
9.
Тетраэдр -Тетраэдр это геометрическое тело из четырех граней, каждая их
которых - правильный треугольник
Правильный тетраэдр составлен из
четырех равносторонних треугольников.
Каждая его вершина является
вершиной трех треугольников.
Следовательно, сумма плоских углов
при каждой вершине равна 180°.
Тетраэдр не имеет центра симметрии,
но имеет 3 оси симметрии и 6
плоскостей симметрии.
Является ли тетраэдр пирамидой? Да,
тетраэдр это треугольная пирамида у
которой все стороны равны.
Может ли пирамида быть тетраэдром?
Только если это пирамида с
треугольным основанием и каждая из её
сторон равносторонний треугольник.
Тетраэдр имеет
следующие
характеристики:
Тип грани –
правильный
треугольник;
Число сторон у
грани – 3;
Общее число
граней – 4;
Число рёбер,
примыкающих к
вершине – 3;
Общее число
вершин – 4;
Общее число
рёбер – 6;
10.
Математическиехарактеристики Тетраэдра
описанной
01Радиус
сферы тетраэдра:
03Площадь
поверхности
тетраэдра:
вписанной
02Радиус
сферы тетраэдра
определяется по
формуле:
тетраэдра
04Объем
определяется по
следующей формуле:
11.
Октаэдр -Октаэдр это геометрическое тело из восьми граней,
каждая их которых - правильный треугольник
Правильный октаэдр составлен из Октаэдр имеет следующие
характеристики:
восьми равносторонних
треугольников. Каждая вершина
● Тип грани – правильный
октаэдра является вершиной
четырех треугольников.
треугольник;
Следовательно, сумма плоских
● Число сторон у грани – 3;
углов при каждой вершине равна
● Общее число граней – 8;
240°.
● Число рёбер, примыкающих к
Октаэдр имеет центр симметрии вершине – 4;
центр октаэдра, 9 осей симметрии
● Общее число вершин – 6;
и 9 плоскостей симметрии.
Общее число рёбер – 12;
12.
Математическиехарактеристики Октаэдра
01
03
02
04
Радиус описанной
сферы октаэдра
определяется по
формуле:
Объем октаэдра
определяется по
следующей
формуле:
Радиус вписанной
сферы октаэдра
определяется по
формуле:
Площадь
поверхности
октаэдра:
13.
Куб (Гексаэдр) -Гексаэдр это геометрическое тело из шести граней,
каждая их которых - правильный четырёхугольник
(квадрат)
Характеристики Гексаэдра:
● Число сторон у грани - 4
● Общее число граней - 6,
форма грани квадрат
● Число рёбер,
примыкающих к каждой
вершине - 3
● Общее число вершин - 8
● Общее число ребер - 12
● Количество пар
параллельных граней - 3
Гранью многогранника
является квадрат. Каждый
из четырех углов равен 90
градусов.
Куб обладает
центром
симметрии
14.
Математические характеристикиГексаэдра
Радиус описанной
сферы куба
определяется по
формуле:
Радиус полувписанной сферы
можно определить по
формуле:
Сфера может быть
вписана внутрь куба.
Площадь поверхности можно
определить как площадь
одной из сторон куба (это
площадь правильного
четырехугольника - квадрата)
умноженной на 6
Радиус вписанной
сферы куба
Объем куба
определяется
по следующей
формуле:
15.
Додекаэдр Додекаэдр имеет следующиехарактеристики:
Тип грани – правильный
пятиугольник;
Число сторон у грани – 5;
Общее число граней – 12;
Число рёбер,
примыкающих к
вершине – 3;
Общее число вершин –
20;
Общее число рёбер – 30.
Додекаэдр это геометрическое тело из двенадцати граней,
каждая их которых - правильный пятиугольник
Правильный додекаэдр
составлен из двенадцати
правильных
пятиугольников. Каждая
вершина додекаэдра
является вершиной трех
правильных
пятиугольников.
Следовательно, сумма
плоских углов при каждой
вершине равна 324°.
Додекаэдр имеет центр
симметрии - центр
додекаэдра, 15 осей
симметрии и 15 плоскостей
симметрии.
16.
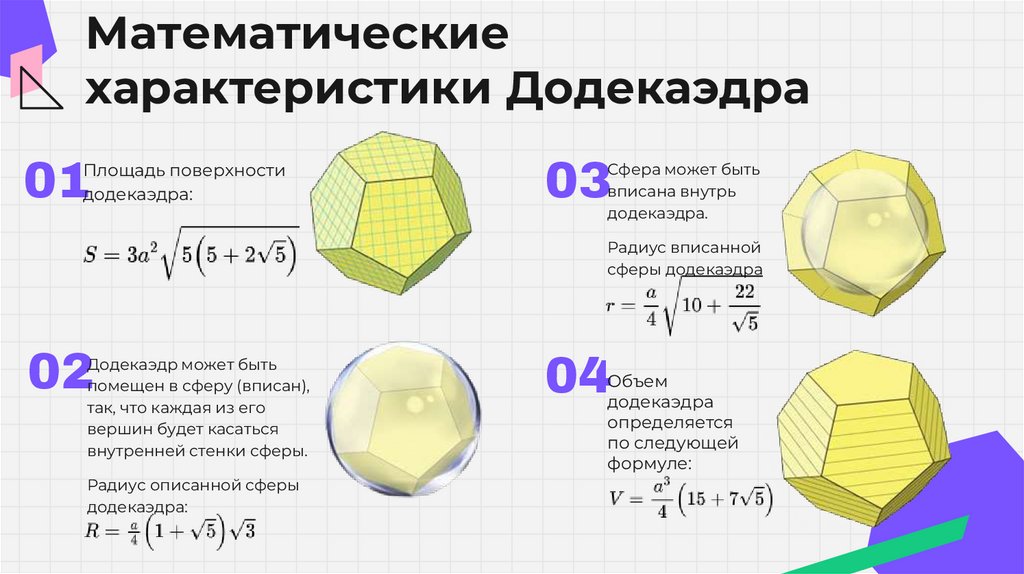
Математическиехарактеристики Додекаэдра
01
Площадь поверхности
додекаэдра:
03
Сфера может быть
вписана внутрь
додекаэдра.
Радиус вписанной
сферы додекаэдра
02
Додекаэдр может быть
помещен в сферу (вписан),
так, что каждая из его
вершин будет касаться
внутренней стенки сферы.
Радиус описанной сферы
додекаэдра:
04
Объем
додекаэдра
определяется
по следующей
формуле:
17.
Икосаэдр -Икосаэдр это геометрическое тело из двадцати граней,
каждая их которых - правильный треугольник
Правильный икосаэдр
составлен из двадцати
равносторонних
треугольников. Каждая
вершина икосаэдра
является вершиной пяти
треугольников.
Следовательно, сумма
плоских углов при
каждой вершине равна
300° (60° x 5).
Икосаэдр имеет центр
симметрии - центр
икосаэдра, 15 осей
симметрии и 15
плоскостей симметрии.
Икосаэдр имеет следующие
характеристики:
Тип грани – правильный
треугольник;
Число сторон у грани – 3;
Общее число граней – 20;
Число рёбер, примыкающих
к вершине – 5;
Общее число вершин – 12;
Общее число рёбер – 30.
18.
Математические характеристикиИкосаэдра
01
Икосаэдр может быть помещен в
сферу (вписан), так, что каждая
из его вершин будет касаться
внутренней стенки сферы.
Радиус описанной сферы
икосаэдра:
02
Сфера может быть вписана внутрь
икосаэдра.
Радиус вписанной сферы
икосаэдра:
03
Площадь поверхности
можно определить как
площадь одной из
сторон икосаэдра (это
площадь правильного
треугольника)
умноженной на 20. Либо
воспользоваться
формулой:
04
Объем икосаэдра
определяется по
следующей формуле:
19.
Спасибо заВнимание
















 mathematics
mathematics








