Математическая обработка статистических данных. Тема 9

1.

Карагандинский университет им. Е.А.Букетова
Методология
научных
исследований
Профессор Сырымбетова Л.С.
Караганда 2023

2.

Тема 9. Математическая обработка статданнызх
Математическая статистика — наука, разрабатывающая
математические методы систематизации и использования
статистических данных для научных и практических
выводов.
Во многих своих разделах математическая статистика
опирается на теорию вероятностей, дающую возможность
оценить надёжность и точность выводов, делаемых на
основании ограниченного статистического материала
(например, оценить необходимый объём выборки для
получения результатов требуемой точности при выборочном
обследовании)

3.

Шкала измерения в статистике — это способ представления переменных
(признаков, атрибутов) и их группировки в различные категории. Она определяет
характер значений, присвоенных переменным в наборе данных.
Шкала измерений формируется на основе двух ключевых понятий —
измерение и масштабирование.
Измерение — это процесс записи наблюдений, собранных в рамках
исследования.
Масштабирование — присвоение объектам числовых значений или
определённой семантики.
Эти два понятия, объединенные вместе, образуют связи между объектами и
наблюдениями.
Шкала измерения используется для определения и описания переменных в
наборах данных. Она определяет методы, которые могут быть использованы для их
анализа.
В зависимости от типа анализируемых данных выделяют 4 основных вида
шкал: номинальная, порядковая, интервальная и шкала отношений.
Номинальная и порядковая шкалы используются для измерения
качественных данных

4.

Номинальная шкала (категориальная, наименований) — это шкала
измерения, которая используется для идентификации. Она присваивает номера
атрибутам для удобства идентификации, но может использоваться только как метка.
Пример: вычисление процентных долей и частот. Данные в номинальной шкале можно
проанализировать графически с помощью гистограммы и круговой диаграммы.
Например, если измерить атрибут «Товар» в номинальной шкале, то она будет
выглядеть так: 1 — мороженное; 2 — соки; 4 — выпечка. При этом значения шкалы не
определяют какого-либо приоритета между товарами, а просто идентифицируют их.
Порядковая шкала (ординальная, ранговая) — предполагает ранжирование
(упорядочивание) значений переменной в зависимости от масштабирования. Атрибуты
в порядковой шкале обычно располагаются в порядке возрастания или убывания.
Порядковая шкала может быть использована в исследованиях рынка, рекламы и
опросов удовлетворенности клиентов. Она использует квалификаторы: «Отлично»,
«Очень хорошо», «Хорошо», «Плохо», «Очень плохо». Атрибуты в этом примере
перечислены в порядке убывания.
Интервальная шкала: устанавливает отношения порядка между интервалами,
расстояниями одних значений признака от других. Имеет произвольный нуль и
произвольную единицу измерения. Пример: температура (различия шкал Цельсия,
Кельвина и Реомюра).
Шкала отношений (абсолютная) является «наивысшим» уровнем

5.

Альфа Кронбаха
Альфа Кронбаха — это способ измерения внутренней согласованности анкеты
или опроса.
Альфа Кронбаха колеблется от 0 до 1, при этом более высокие значения
указывают на то, что опрос или анкета более надежны.
Значения альфа Кронбаха (внутренняя согласованность):
0,9 ≤ α
Превосходно
0,8 ≤ α < 0,9
Хороший
0,7 ≤ α < 0,8
Приемлемый
0,6 ≤ α < 0,7
Сомнительный
0,5 ≤ α < 0,6
Бедный
α < 0,5
Неприемлемо
Переход в Excell

6.

Коэффициент корреляции Пирсона
Коэффициент корреляции Пирсона (r-Пирсона) применяется для исследования
взаимосвязи двух переменных, измеренных в метрических шкалах на одной и той
же выборке. Он позволяет определить, насколько пропорциональная изменчивость
двух переменных.
Коэффициент корреляции изменяется в пределах от минус единицы до плюс
единицы.
Коэффициент корреляции r-Пирсона характеризует существование линейной связи
между двумя величинами.
Чтобы приступать к расчетам коэффициента корреляции r-Пирсона необходимо
выполнение следующих условий:
исследуемые переменные X и Y должны быть распределены нормально.
исследуемые переменные X и Y должны быть измерены в интервальной шкале
или шкале отношений.
количество значений в исследуемых переменных X и Y должно быть одинаковым

7.

Формула вычисления коэффициента
корреляции Пирсона

8.

Расчет коэффициента корреляции Пирсона в Excell
Для того, чтобы рассчитать коэффициент корреляции Пирсона в Excell
необходимо сделать следующие шаги:
1.Вносим значения для двух переменных в таблицу (Например Переменная 1 и
Переменная 2)
2. Ставим курсор в пустую ячейку
3. На панеле инструментов нажимаем кнопку fx (вставить формулу)
4. В открывшемся окне «Мастер функций» в поле «Категории» выбираем Полный
алфавитный перечень
5. Затем в поле «Выберите функцию» находим функцию ПИРСОН
5.1. Нажимаем Ок
6. В открывшемся окне «Аргументы функции» в поле Массив1 вносим номера
ячеек, содержащие значения Переменной 1, в поле Массив2 вносим номера ячеек,
содержащие значения Переменной2.
7. Нажимаем Ок
8. Смотрим получившийся результат
Переход в Excell

9.

Таблица Чеддока
слабая — от 0,1 до 0,3;
умеренная —
от 0,3 до 0,5;
заметная —
от 0,5 до 0,7;
высокая — от 0,7 до 0,9;
сильная — от 0,9 до 1,0
Коэффициент ранговой корреляции Спирмена
Коэффициент корреляции Спирмена (Spearman rank correlation
coefficient) — мера линейной связи между случайными величинами.
Корреляция Спирмена является ранговой, то есть для оценки силы
связи используются не численные значения, а соответствующие им ранги.
Переход в Excell

10.

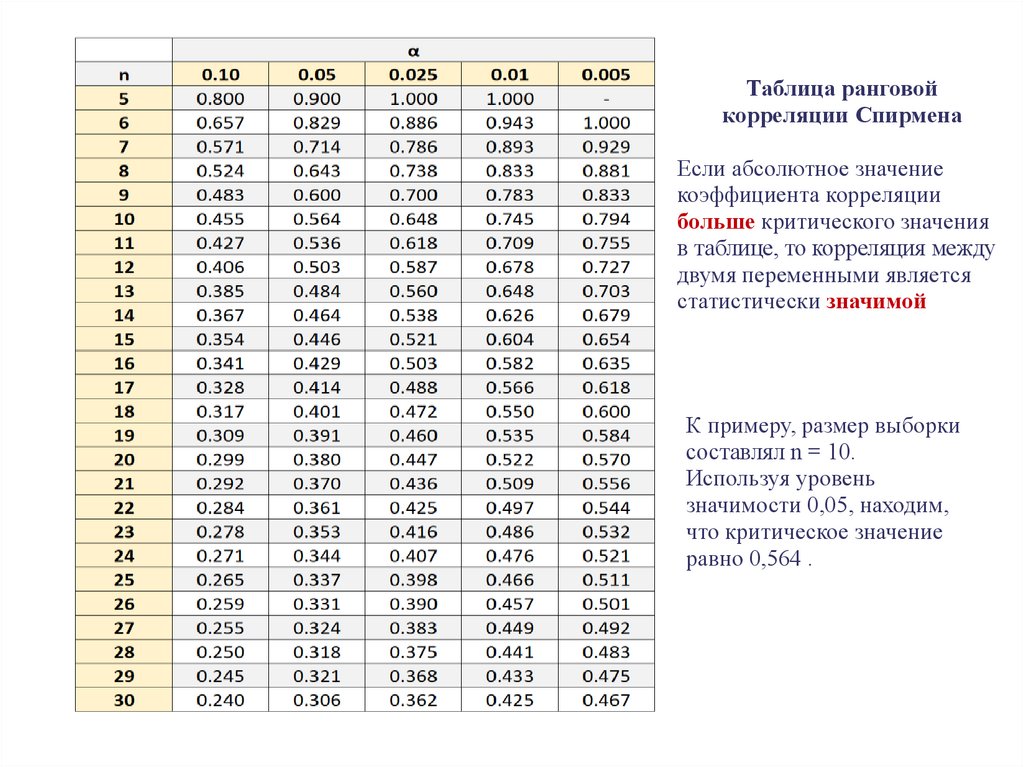
Таблица ранговой
корреляции Спирмена
Если абсолютное значение
коэффициента корреляции
больше критического значения
в таблице, то корреляция между
двумя переменными является
статистически значимой
К примеру, размер выборки
составлял n = 10.
Используя уровень
значимости 0,05, находим,
что критическое значение
равно 0,564 .

11.

Критерий независимости Пирсона χ2 (Хи-квадрат)
Это анализ категориальных данных, т.е. таких, которые выражаются не количеством, а
принадлежностью к какой-то категории. Например, класс автомобиля, пол участника
эксперимента, вид растения и т.д. К таким данным нельзя применять математические
операции вроде сложения и умножения, для них можно только подсчитать частоты
Формула критерия Пирсона χ2
Данный критерий имеет нулевые и альтернативные гипотезы:
H0 (нулевая гипотеза): две переменные независимы.
H1 (альтернативная гипотеза): две переменные не являются
независимыми. (т.е. они связаны)
Формула для расчета: Х2 = Σ(ОЕ)2/Е
Где:
Σ:
«сумма»
O (Observed):
наблюдаемое значение
E (Expected):
ожидаемое значение

12.

Пример
Мы хотим знать, связан ли пол с предпочтениями политических партий, поэтому мы
опрашиваем 500 избирателей и фиксируем их пол и предпочтения политических
партий. То есть мы хотим знать, связаны ли две категориальные переменные друг с
другом.
Чтобы определить, существует ли статистически значимая связь между
переменными, применяется критерий независимости Хи-квадрат.
Шаг 1. Определение гипотезы
H0: Пол и предпочтения политической партии не зависят друг от друга.
H1: Пол и предпочтение политической партии не являются независимыми.
Шаг 2. Рассчет ожидаемых значений по формуле:
Ожидаемое значение = (сумма строк * сумма столбцов) / сумма таблицы.
Шаг 3. Рассчет (OE)2/E для каждой ячейки таблицы, где:
O: наблюдаемое значение
E: ожидаемое значение
Шаг 4. Рассчет тестовой статистики X2 и соответствующее значение p по
формуле: X2 = Σ(OE)2 / E
Переход в Excell

13.

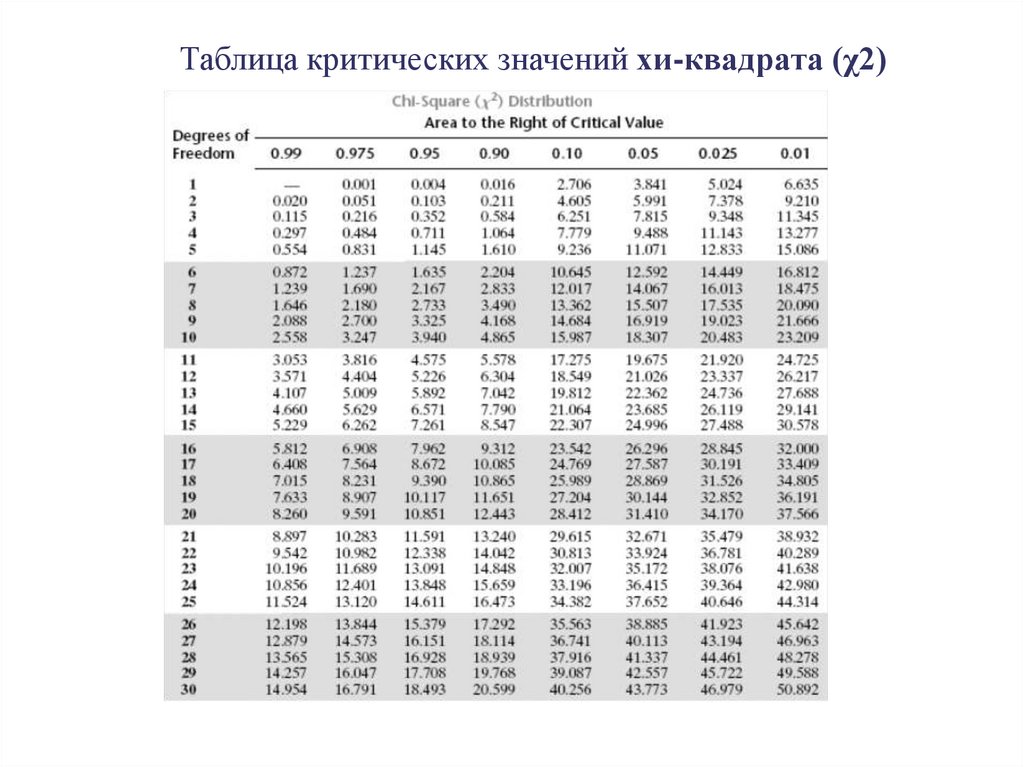
Таблица критических значений хи-квадрата (χ2)

14.

Обратная связь. Тема 9. Статанализ
Тест №1
https://forms.gle/UppirhBdGeAHHzLV6
Тест 2.
https://forms.gle/j4XNgy5e6MeN4DrC9

15.

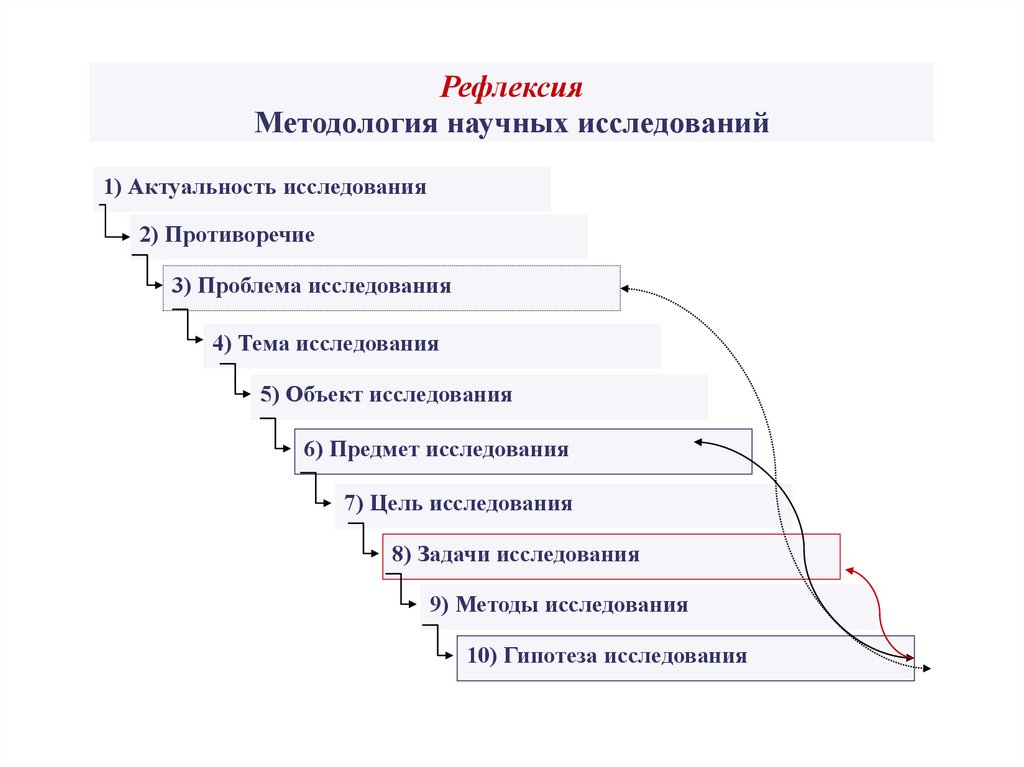
Рефлексия
Методология научных исследований
1) Актуальность исследования
2) Противоречие
3) Проблема исследования
4) Тема исследования
5) Объект исследования
6) Предмет исследования
7) Цель исследования
8) Задачи исследования
9) Методы исследования
10) Гипотеза исследования