Уравнение sin x = b

1.

Уравнение sin x = b

2.

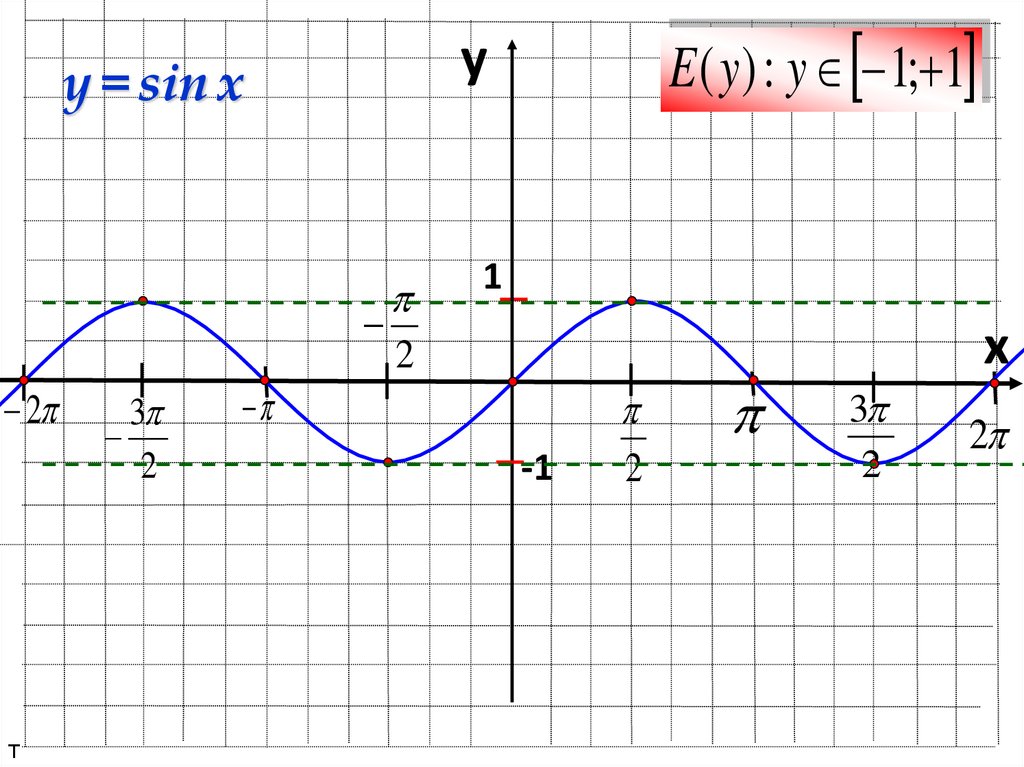
y = sin x
2
2
т
3
2
E ( y) : y 1; 1
y
1
-1
2
x
3
2
2

3.

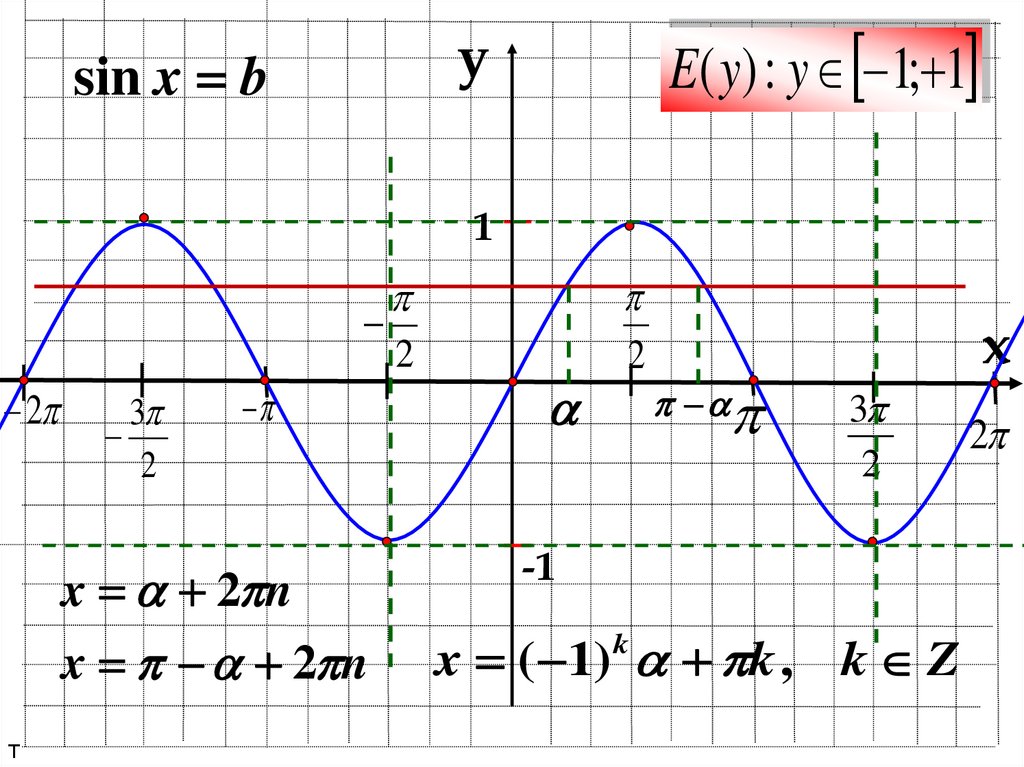
E( y) : y 1; 1
y
sin x b
1
2
2
3
2
x 2 n
x 2 n
т
2
x
3
2
-1
x ( 1) k , k Z
k
2

4.

sin x b
x ( 1) k , k Z
k
α – арксинус b
Арксинусом числа b, где
b 1, называют такое число α
из промежутка [ ; ] , синус
2 2
которого равен b.

5.

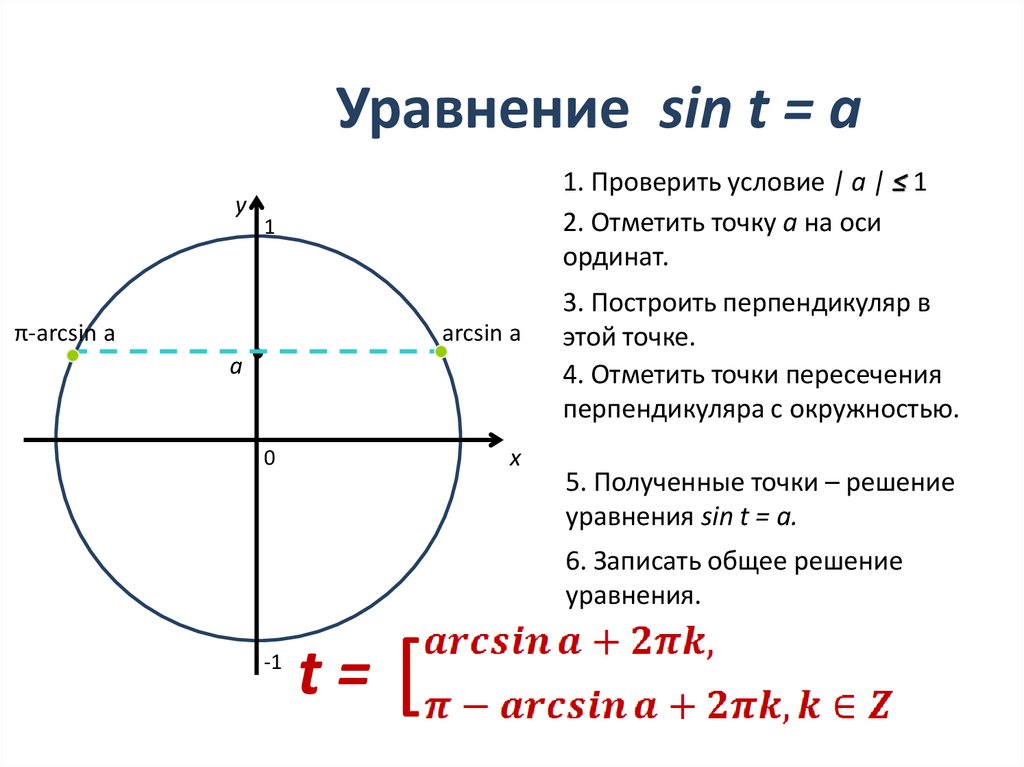
Уравнение sin t = a
y
1. Проверить условие | a | ≤ 1
2. Отметить точку а на оси
ординат.
1
π-arcsin a
arcsin a
a
x
0
3. Построить перпендикуляр в
этой точке.
4. Отметить точки пересечения
перпендикуляра с окружностью.
5. Полученные точки – решение
уравнения sin t = a.
6. Записать общее решение
уравнения.
-1
t= [

6.

[

7.

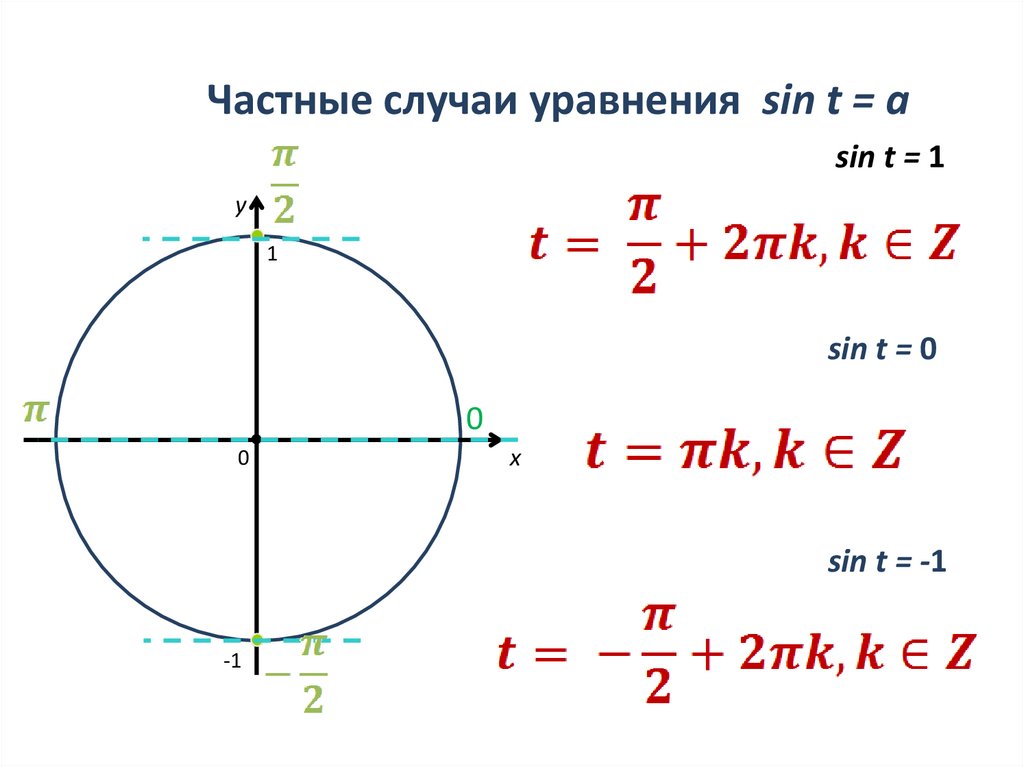
Частные случаи уравнения
sin x = b
sin x 0
sin x 1
x
2
2πn, n Z
x n, n Z
sin x 1
x
2
2πn, n Z

8.

Частные случаи уравнения sin t = a
sin t = 1
y
1
sin t = 0
0
0
x
sin t = -1
-1

9.

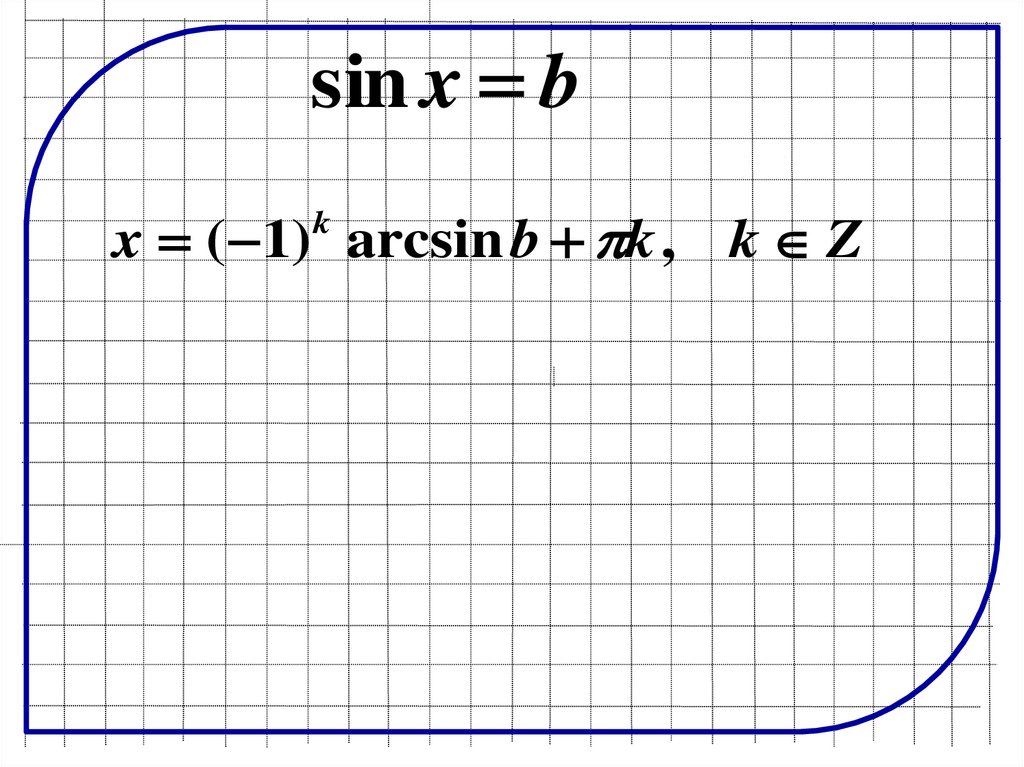
sin x b
x ( 1) k , k Z
k
α = arcsin b
1
1
arcsin ,
[ ; ] sin
2 6
6
2 2
6 2
3
3
arcsin(
) , [ ; ] sin( )
2
3
3
2 2
3
2

10.

sin x b
x ( 1) arcsin b k , k Z
k

11.

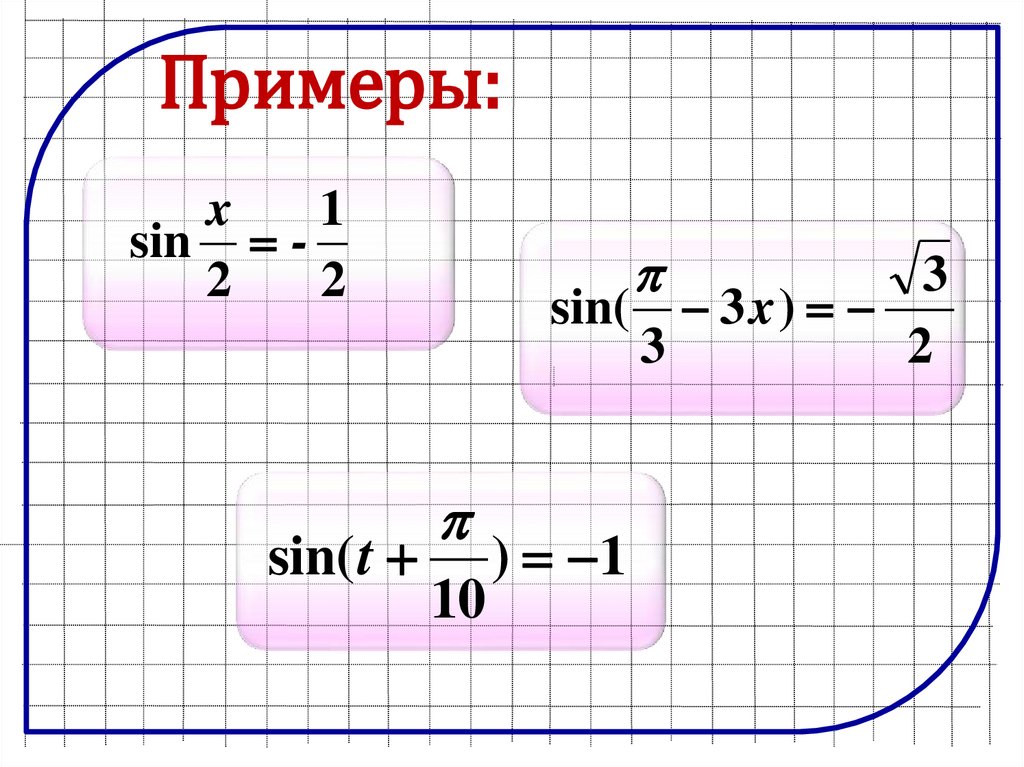
Примеры:
x
1
sin 2
2
sin( t
3
sin( 3 x )
3
2
10
) 1