Противоположное событие. Диаграммы Эйлера

1.

Противоположное
событие.
Диаграммы Эйлера

2.

Напомним:
Случайный опыт (случайный эксперимент) - математическая абстракция,
описывающая реальный опыт, который может оканчиваться различными
событиями
Случайный опыт оканчивается каким-либо одним элементарным
событием. Какое именно элементарное событие наступает в данном опыте –
дело случая. Два различных элементарных
события одновременно
произойти не могут.
Случайное событие или просто событие – это некоторое множество (набор,
совокупность) элементарных событий.
Случайное событие A наступает, когда происходит какое - либо
элементарное событие, благоприятствующие событию A.

3.

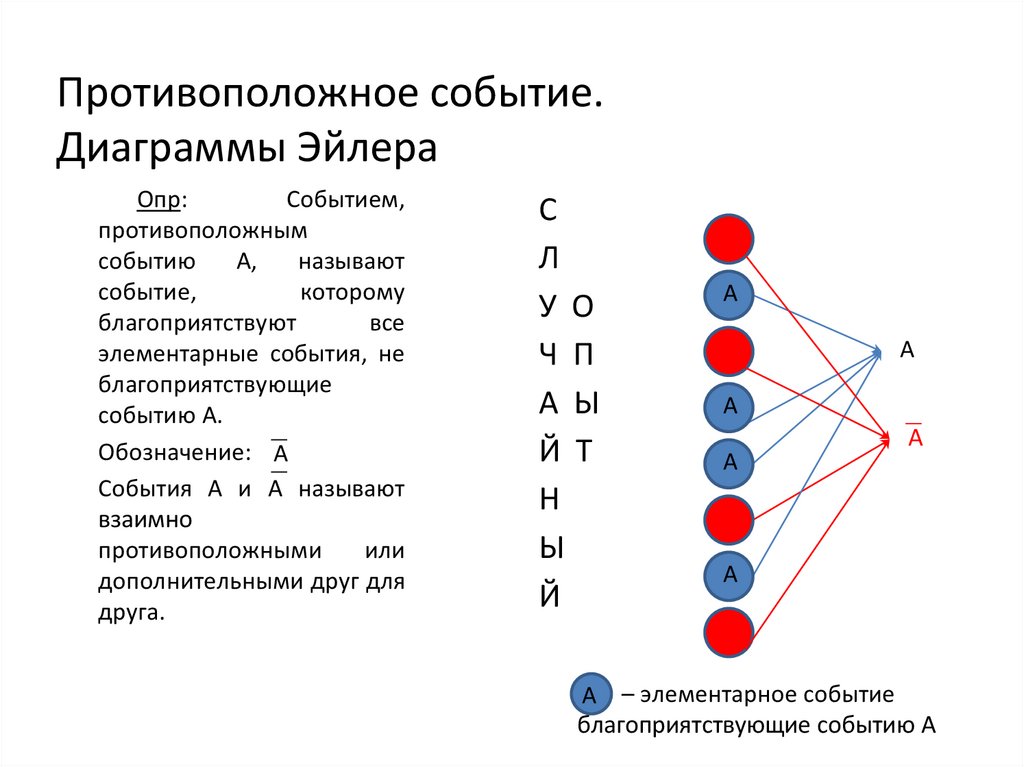
Противоположное событие.
Диаграммы Эйлера
Опр:
Событием,
противоположным
событию
А,
называют
событие,
которому
благоприятствуют
все
элементарные события, не
благоприятствующие
событию А.
Обозначение: А
События А и А называют
взаимно
противоположными
или
дополнительными друг для
друга.
С
Л
У О
Ч П
А Ы
Й Т
Н
Ы
Й
А
А
А
А
А
А
А – элементарное событие
благоприятствующие событию А

4.

Пример
Бросают игральную кость. Рассмотрим событие А «выпало число, большее 4».
Этому событию благоприятствуют элементарные события «выпала пятёрка» и «выпала
шестёрка». Не благоприятствуют событию А следующие элементарные события:
«выпала единица», «выпала двойка», «выпала тройка», «выпала четвёрка» (см. рис.).
Для события А противоположным событием А является событие «выпало число,
меньшее или равное четырём».
Событие А
Событие А
Взаимно противоположные события одновременно произойти не могут, но какое –
либо из них происходит обязательно. Поэтому
Р(А) + Р(А) = 1.
Иными словами, сумма вероятностей взаимно противоположных событий равна
единице.
Следовательно,
Р(А) = 1 – Р(А) и Р(А) = 1 – Р(А)
Из этих формул следует что для вычисления Р(А) достаточно знать Р(А) Это свойство
во многих случаях оказывается полезным.

5.

Свойства противоположных событий
1) Если В = А, то А = В
2) Взаимно противоположные события одновременно произойти не могут,
но какое – либо из них происходит обязательно.
Р(А) + Р(А) = 1
3) Для вычисления Р(А) достаточно знать Р(А).
Р(А) = 1 – Р(А)
Р(А) = 1 – Р(А)

6.

Диаграммы Эйлера
Соотношения и связи между
событиями можно изобразить с
помощью схематических рисунков
– диаграмм Эйлера.
Если
нужно
изобразить
несколько событий, то рисуют
несколько фигур – по одной для
каждого события. При этом
фигуры могут располагаться по –
разному, показывая, как связаны
между собой данные события.
Событие А
А
Событие А,
противоположное
А

7.

Решение задач:
1. Игральный кубик бросили дважды.
Найдите вероятность того, что:
а) среди выпавших чисел есть хотя бы одна единица;
Решение: Общее число возможных исходов при бросании кубика равно
N = 6*6 = 36 исходов .
а) исходов в которых нет ни одной единицы, всего 5*5=25.
Следовательно, P(A) = 1- 25/36 = 11/36;
б) сумма выпавших чисел не больше 3;
Решение: б) исходов в которых сумма выпавших чисел не больше 3,
всего три ( это 1-1, 1-2, 2-1 ), поэтому N(В) =3 , P(В) = 3/36=1/12
в) сумма выпавших чисел меньше 11;
Решение: исходов в которых сумма выпавших чисел меньше 11, всего
N(С)=36-3=33 ( т. к. исходов в которых сумма чисел не меньше 11,
три, т. е. 5-6, 6-5, 6-6), P(С) = 33/36=11/12

8.

2) Случайным образом выбирают натуральное число из
промежутка .
Найдите вероятность того, что:
а) оно не оканчивается нулём;
Решение: Промежуток содержит 100 целых чисел. N=100, выбор
любого из этих чисел равновозможен.
Рассмотрим событие: А – « Выбранное число не оканчивается
0»
Количество благоприятных исходов для каждого их этих событий
подсчитаем, исключив «ненужные» варианты.
Количество чисел оканчивающихся нулём равно
N(A) = N – 10 = 90 . P(A) = N(A)/ N = 90/100 = 0,9 или
другим способом: Р(А) = 1 – Р(А-) = 1-10/100=90/100=0,9.

9.

2) Случайным образом выбирают натуральное число из
промежутка .
Найдите вероятность того, что:
б) среди его цифр есть хотя бы одна большая двух
Решение: Промежуток содержит 100 целых чисел. N=100, выбор
любого из этих чисел равновозможен.
Рассмотрим событие: В – « среди цифр выбранного числа, есть хотя бы
одна цифра большая двух»
Количество благоприятных исходов для каждого их этих событий
подсчитаем, исключив «ненужные» варианты.
Количество чисел, составленных только из цифр не больше 2 (0;1;2)
равна 9 (100, 101, 102, 110, 111, 112, 120, 121, 122) на этом
промежутке.
N(В) = N – 9 = 91 . P(В) = N(В)/ N = 91/100 = 0,91 или
другим способом: Р(В) = 1 – Р(В-) = 1-9/100=91/100=0,91.

10.

2) Случайным образом выбирают натуральное число из
промежутка .
Найдите вероятность того, что:
в) оно не является квадратом другого целого числа;
Решение: Промежуток содержит 100 целых чисел. N=100, выбор
любого из этих чисел равновозможен.
Рассмотрим событие: С – « выбранное число не является квадратом
другого целого числа»
Количество благоприятных исходов для каждого их этих событий
подсчитаем, исключив «ненужные» варианты.
Количество чисел, являющихся квадратом целого числа,
подсчитаем непосредственно: 100, 121, 144, 169, 196 –
всего 5 чисел, поэтому
N(С) = N – 5 = 95 . P(С) = N(С)/ N = 95/100 = 0,95 или
другим способом: Р(С) = 1 – Р(С-) = 1-5/100=95/100=0,95.

11.

.
2) Случайным образом выбирают натуральное число из
промежутка .
Найдите вероятность того, что:
г) сумма его цифр меньше 17.
Решение: Промежуток содержит 100 целых чисел. N=100, выбор
любого из этих чисел равновозможен.
Рассмотрим событие: D – «сумма цифр выбранного числа меньше 17».
Количество благоприятных исходов для каждого их этих событий
подсчитаем, исключив «ненужные» варианты.
Количество чисел, сумма цифр которых не меньше 17,
будет 100 .
N(Д) = N – 100 = 0 . P(С) = N(С)/ N = 0/100=0

12.

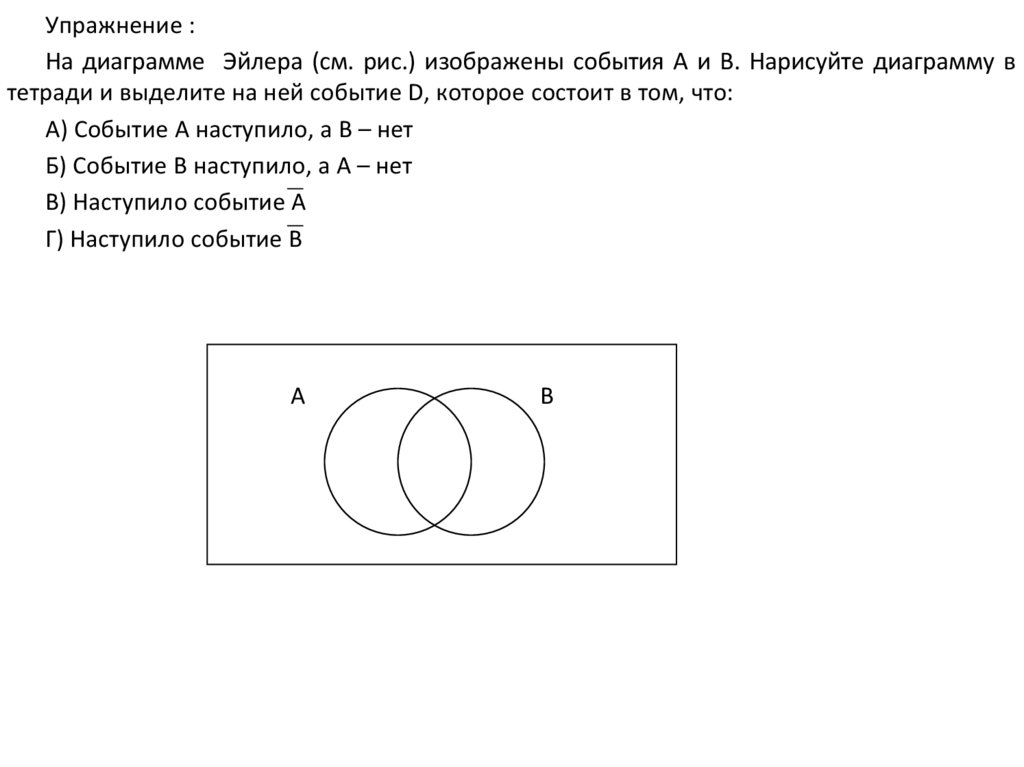
Упражнение :
На диаграмме Эйлера (см. рис.) изображены события А и В. Нарисуйте диаграмму в
тетради и выделите на ней событие D, которое состоит в том, что:
А) Событие А наступило, а В – нет
Б) Событие В наступило, а А – нет
В) Наступило событие А
Г) Наступило событие В
А
В

13.

Домашнее задание
1) Событие А – « на игральной кости выпало
меньше 5 очков». Что означает событие А ?
Выразите значение Р(А) в процентах.
2) Наугад называется натуральное число от 1 до 30.
Какова вероятность того, что это число не 15?
3) В лотерее 1000 билетов, среди которых 20
выигрышных. Приобретается один билет. Какова
вероятность того, что этот билет:
1) выигрышный; 2) невыигрышный.
4) В кооперативном доме 93 квартиры, из которых три
находится на первом этаже, а 6 на последнем. Квартиры
распределяются по жребию. Какова вероятность того, что
жильцу не достанется квартира, расположенная на первом
или последнем этаже?