Моделирование процесса производства. Тема 2

1.

2. Моделирование процесса
производства

2.

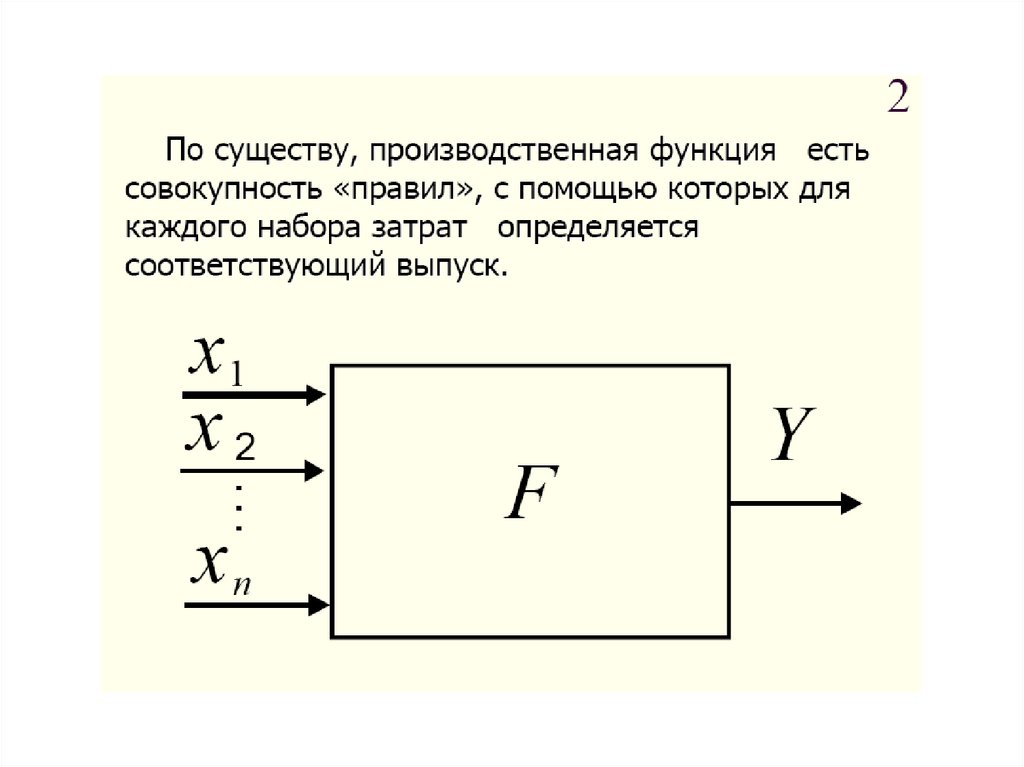
2.1. Производственные функции и их
свойства

3.

4.

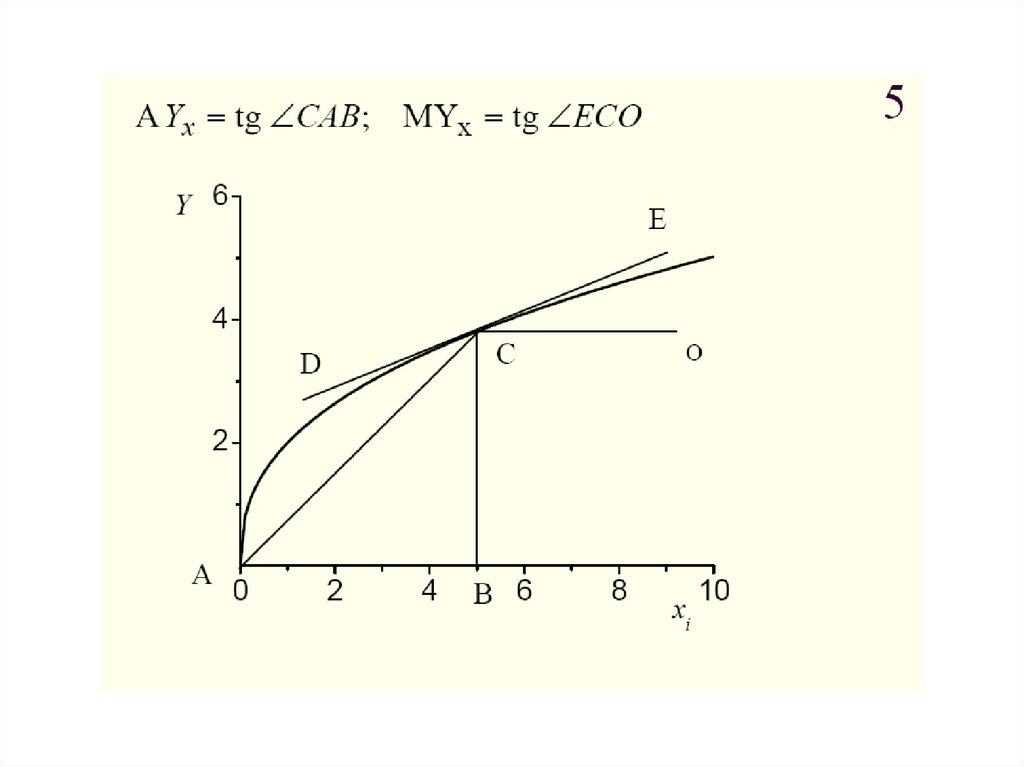
5.

Неоклассическая производственная
функция обладает следующими
свойствами:

6.

7.

8.

5. Производственная функция должна обладать
свойством масштабируемости (при увеличении объема
всех ресурсов в l раз, объем производства Y возрастает
как lgY
*

9.

Напомним, что A и a в этой функции – константы,
характеризующие особенности производственного
процесса, K – стоимость капитальных ресурсов, L –
трудовых.
Еще один пример – мультипликативная
производственная функция
Y=A Ka Lb

10.

11.

12.

Характеристики производственной
функции

13.

14.

15.

16.

17.

18.

19.

20.

21.

22.

23.

24.

25.

26.

2.2. Производственные функции с
постоянной эластичностью
замещения факторов производства

27. Замещение ресурсов в процессе производства

28.

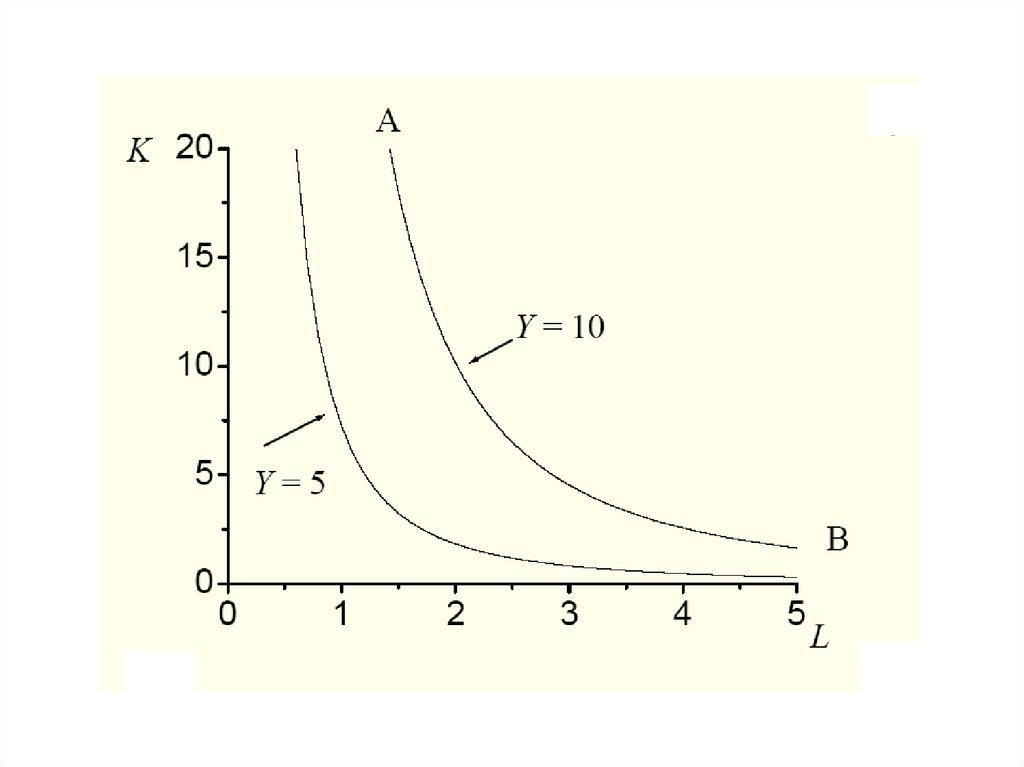
Рассмотрим производственную функцию из
предыдущего примера:
Мы можем зафиксировать выпуск на некотором
уровне Y0.

29.

30.

31.

32.

33.

34.

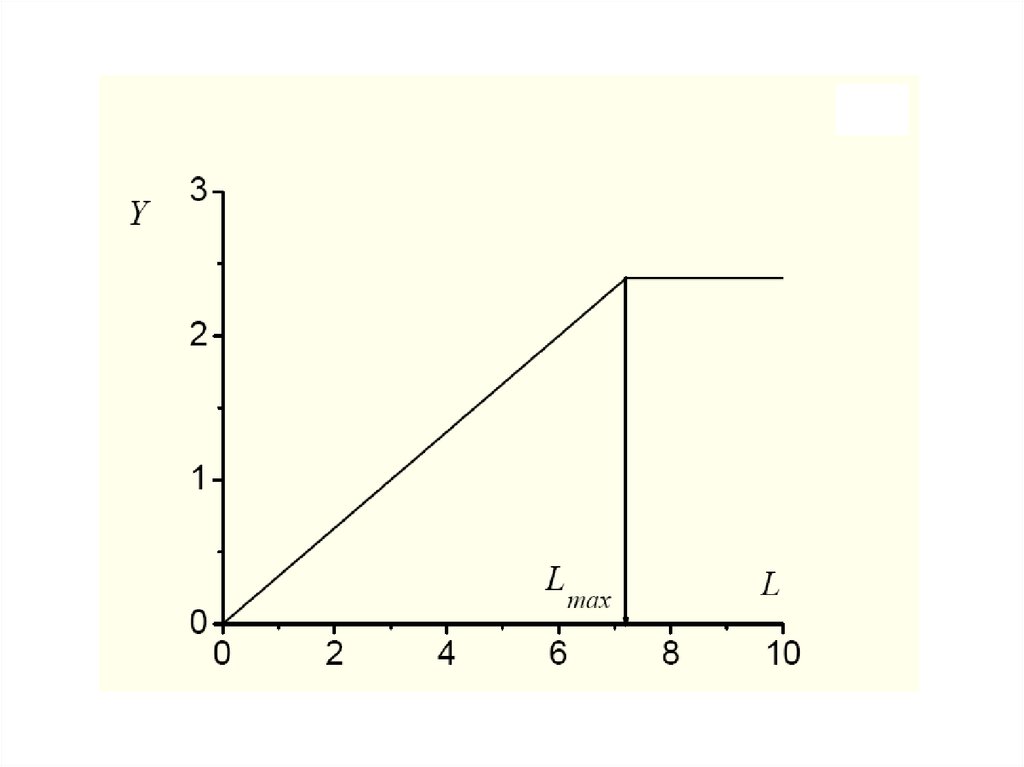
35. Если в процессе производства замена одного фактора другим невозможна, для его описания нельзя использовать неоклассическую

производственную
функцию. Примером производственной функции,
описывающей производственный процесс с жестким
производственным циклом является производственная
функция Леонтьева.
Y ( K , L) min c1 K , c2 L
K L
Y ( K , L) min , .
a b
Коэффициенты c1 и с2 зависят от количества ресурса,
необходимого для производства единицы товара (a, b).

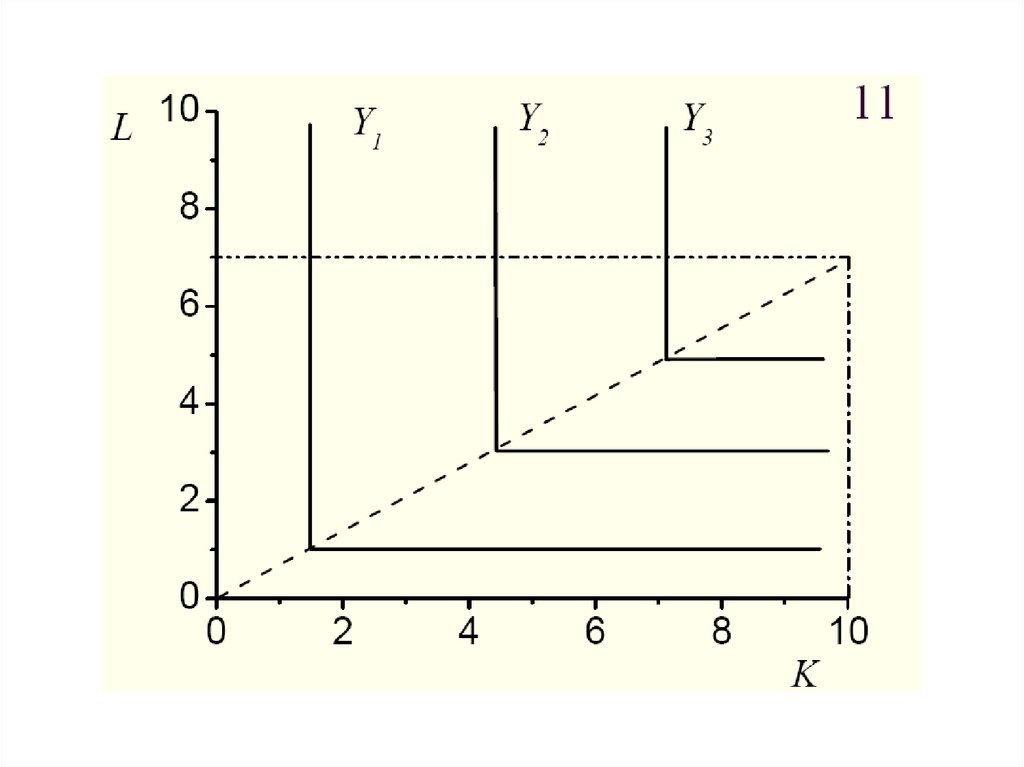
36. Чтобы построить множество изоквант производственной функции Леонтьева, необходимо сначала построить прямую K=a/bL. На этой

прямой
будут лежать точки, соответствующие
производственным процессам, идущим с полным
использованием всех ресурсов.
Далее, выбранную на этой прямой точку
необходимо дополнить вертикальными и
горизонтальными прямыми, соответствующими
производственным процессам с тем же объемом
выпуска, но с избыткам одного из ресурсов (см.
след. слайд)

37.

38.

39.

40.

41.

Предельная норма замещения факторов
производства

42.

Рассмотрим производственную функцию,
допускающую замещение одного фактора
производства другим. Из условия сохранения объема
выпуска при таком замещении (Y=const) следует, что
малые приращения участвующих в замене факторов
подчиняются следующему соотношению:
Y
Y
dxi
dx j 0.
xi
x j
Предельную норму замещения одного фактора
производства другим определим соотношением
Y
dx j
x
M ij
i ,
Y
dxi
x j

43.

Полученную формулу предельной нормы замещения
факторов производства можно записать, используя
определение предельных величин и определение
эластичности:
M ij
M Yx i
M Yx j
xi x j
x j xi

44.

Предельная норма замещения труда капиталом
показывает, какое дополнительное количество капитала
может скомпенсировать уменьшение задействованных в
экономике трудовых ресурсов на единицу так, чтобы
уровень производства не изменился
Предельная норма замещения труда капиталом численно
равна тангенсу угла наклона касательной к изокванте.
dK
M LK
dL

45.

Предельная норма замещения труда капиталом прямо
пропорциональна фондовооруженности k=K/L
L K 0,594 5258 ,03
M LK
76,93
K L 0,539 75,325
При условии постоянства эластичности по труду и
капиталу
(например,
для
мультипликативной
производственной функции) правая часть формулы
зависит только от фондовооруженности k = K/L, которая
остается постоянной вдоль любого луча, выходящего из
начала координат на диаграмме, построенной в осях K и
L. Таким образом, предельная норма замещения труда
капиталом также остается постоянной вдоль таких
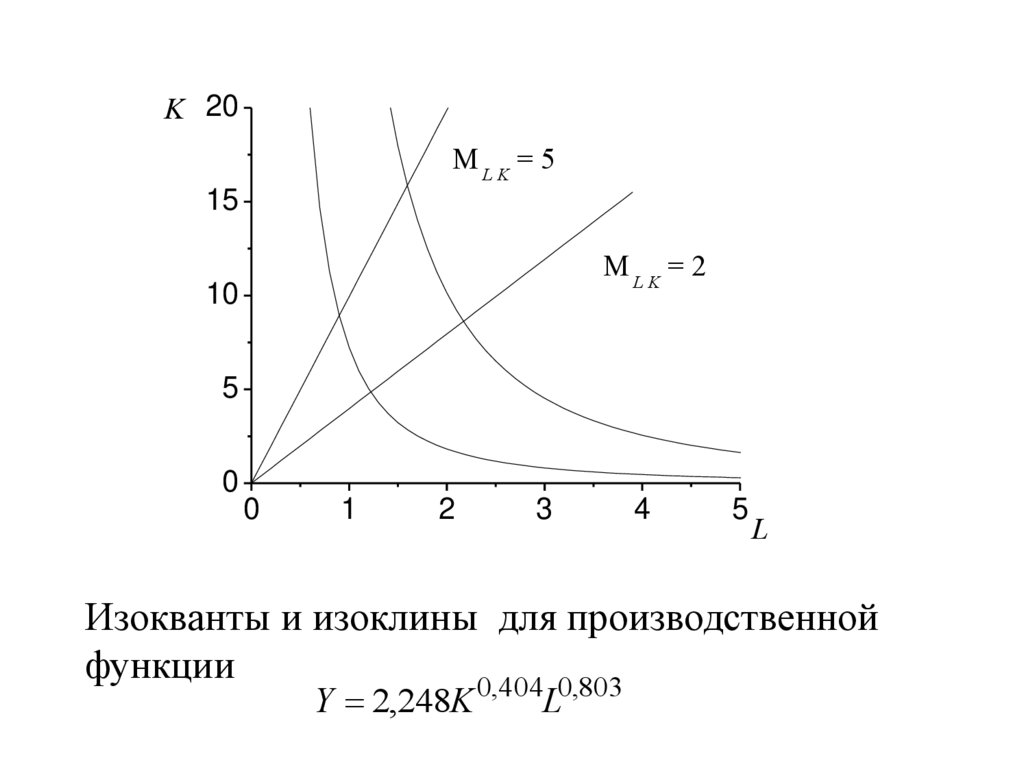
лучей. Лучи k = K/L=const называются изоклинами.

46.

K 20
MLK = 5
15
MLK = 2
10
5
0
0
1
2
3
4
5
L
Изокванты и изоклины для производственной
функции
0,404 0,803
Y 2,248K
L

47.

Эластичность замещения труда капиталом равна
величине относительного изменения
фондовооруженности в условиях фиксированного
выпуска при относительном изменении предельной нормы
замещения труда капиталом на 1 процент:
k
M LK
M LK
k

48.

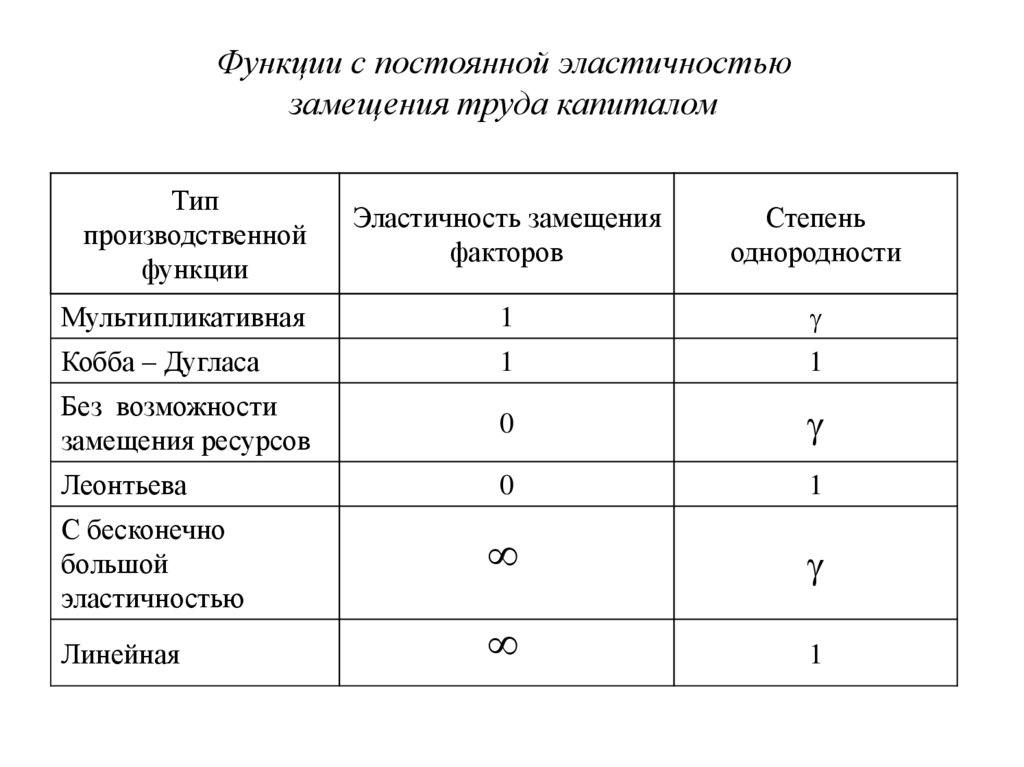
Функции с постоянной эластичностью
замещения труда капиталом
Тип
производственной
функции
Эластичность замещения
факторов
Степень
однородности
Мультипликативная
1
g
Кобба – Дугласа
1
1
Без возможности
замещения ресурсов
0
g
Леонтьева
0
1
С бесконечно
большой
эластичностью
g
1
Линейная

49.

Без возможности замещения ресурсов
Y ( K , L) lim c1 K c2 L
g
min c1 K g , c2 Lg
С бесконечно большой эластичностью
Y ( K , L) c1 K c2 L
g
Линейная
Y ( K , L) c1 K c2 L g

50.

2.3. Модель В. Леонтьева «Затраты выпуск»

51.

52.

53.

54.

55.

56.

57.

58.

59.

60.

61.

62.

63.

64.

65.

66.

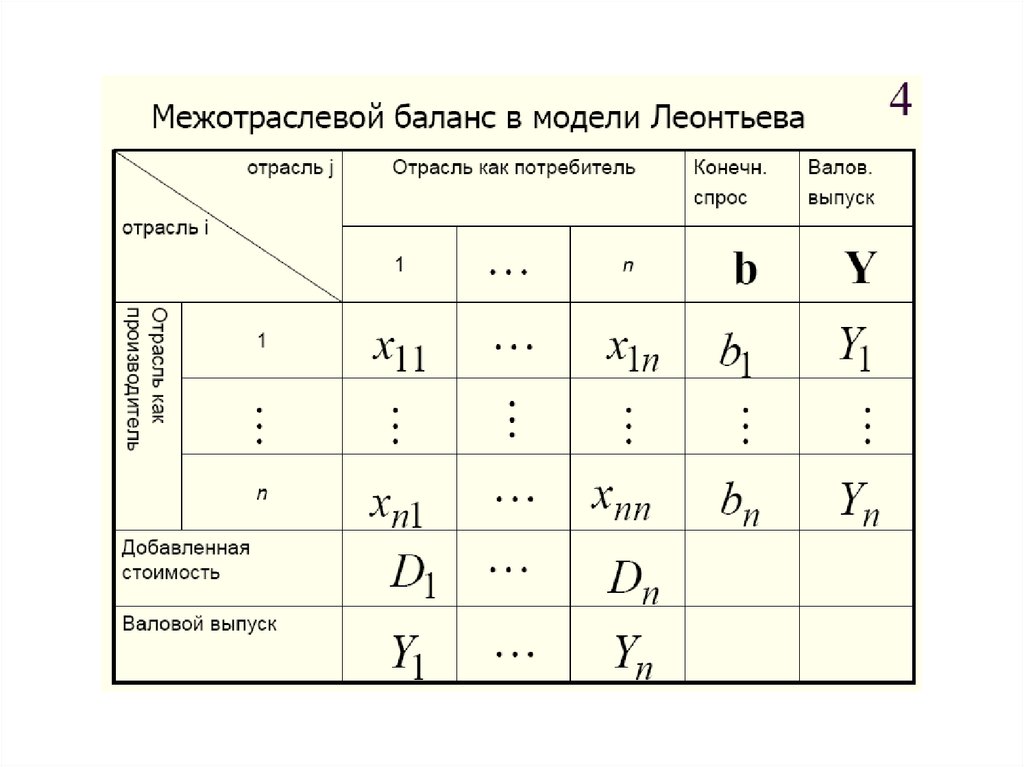
Таблица и тождества межотраслевого баланса

67.

68.

69.

70.

71.

72.

73.

74.

Возможность складывать значения в столбце матрицы
межотраслевых поставок существует только в случае, когда все
рассмотренные в модели Леонтьева величины ( конечный
продукт, валовый выпуск, межотраслевые поставки) приведены
в ценовом выражении.
Основное уравнение модели Леонтьева сохраняет свою форму
независимо от того, выражаются ли входящие в него величины
в количественных или ценовых единицах.
Обозначим вектор валового выпуска, выраженный в единицах
произведенной продукции как Y*, конечный продукт как b*,
матрицу технологических коэффициентов как A*, а матрицу
межотраслевых поставок как X*, тогда
Y*+A*Y*=b*.

75.

При заданном векторе цен pT=(p1, p2, p3…pn) можно записать
следующие
формулы,
связывающие
матрицы
модели,
представленные в ценовом и количественном выражении:
Yj=pjYj*, bi=bi*pi,
aij=aij*pi/pj,
xij=xij*pi.
Для того, чтобы вычислить стоимость межотраслевых поставок из
отрасли i в отрасль j, необходимо объем таких поставок,
выраженный в единицах продукции, умножить на цену единицы
продукции отрасли i.
Чтобы рассчитать, стоимость продукции, поставляемой из
отрасли i, приходящуюся на единицу стоимости продукции
отрасли j, необходимое количество продукции aij* умножается на
цену продукции отрасли i и делится на цену продукции отрасли j.

76.

Согласно рассмотренным формулам, для добавленной стоимости
можно записать следующее выражение:
Dj=Yj – (x1j+x2j+…+xnj)
Разделив обе части на Yj, для доли добавленной стоимости
в валовом выпуске отрасли легко получить выражение:
j=1– (a1j+a2j+…+anj)
Если же обе части исходной формулы разделить на Yj*,
получим :
j*=(1– (a1j+a2j+…+anj)) pj= j pj,
где j* – норма добавленной стоимости – величина,
показывающая,
чему равен вклад в цену единицы
продукции, добавленный отраслью в процессе ее
производства.

77.

Для вектора норм добавленной стоимости выполняется
следующее соотношение:
*=(I– A*T) p,
Чтобы его получить, можно заменить элементы матрицы A на
A* в предыдущей формуле в соответствии с приведенными
выше соотношениями, что дает
j*=pj– (a1j* p1 +a2j*p2 +…+anj*pn) .